Флуктуационный объем и параметр Грюнайзена в области перехода жидкость-стекло

В ряде молекулярно-кинетических процессов в жидкостях и аморфных средах важную роль играет предельная упругая деформация межатомной связи Arm, которая обусловлена критическим смещением кинетической единицы из равновесного положения Arm, соответствующим максимуму силы межатомного притяжения. Кинетическая единица (атом, группа атомов), способная к такому крити- ческому смещению, названа "возбужденным атомом", а сам подход – моделью возбужденного состояния [1, 2].

Флуктуационный объем аморфной системы обусловлен критическими смещениями возбужденных частиц из равновесных положений [2]

AV e = N e AV e , где N_e - число возбужденных атомов, Au _e - элементарный флуктуационный объем, необходимый для возбуждения (критического смещения) атома: ^Аи e = ^П d ^А r m , n d² - площадь эффективного сечения атома.

Доля флуктуационного объема f = ( Δ V e /V) выражается формулой [2]

г Аи

f = —^L exp и

—

AH )

e

Т )

где A H_e - энтальпия возбуждения атома, u =V/N - атомный объем.

Возбуждение атома связано с его значительным флуктуационным смещением из равновесного положения, при котором нарушается линейная зависимость силы межатомного притяжения от смещения атома и проявляется ангармонизм колебаний решетки, мерой которого служит параметр Грю-

найзена y d .

Настоящее сообщение посвящено установлению определенной взаимосвязи между долей флуктуационного объема f = f g при температуре стеклования T = T _g и параметром Грюнайзена y d для аморф-

ных органических полимеров и неорганических стекол.

Легко убедиться, что для коэффициента теплового расширения флуктуационного объема β f = (d f /dT) P из уравнения (1) следует соотношение

в f = f

AHe kT2

откуда, используя для ( A H e / kT) зависимость (1), имеем

β f T = f ln(1/ f ),                            (2)

где учтено, что Au _e и и по порядку величины близки ( Ao _e/ o® 1), поскольку Au _e представляет собой минимальный флуктуационный объем, куда может перескочить соседний атом с объемом и [2].

Коэффициент объемного теплового расширения (КТР) стеклующегося расплава в l можно представить в виде суммы двух слагаемых [3, 4]

β l = β g + β f ,                                 (3)

где P _g - КТР стекла ниже T _g, обусловленный пропорциональным увеличением среднего межатомного расстояния, p _f - структурное слагаемое, равное КТР флуктуационного объема жидкости, который обусловлен изменением взаимных расположений частиц относительно друг друга в результате их локальных перегруппировок. В этих перегруппировках решающую роль играет ангармонизм колебаний возбужденных атомов, который выражен значительно сильнее, чем ангармонизм колебаний атома в узлах решетки твердого стекла.

В КТР расплава в l доминирующий вклад вносит структурная составляющая p _f, наличием которой объясняется существенно больший КТР жидкостей в сравнении с КТР твердых тел. Согласно (3), ве-

личина p f равна скачку КТР при температуре стеклования T _g P f = (P i + в д ) = А в

Принимая это во внимание и f = f g при T = T g , соотношение (2) запишем в виде

Ав Tg = f ln1 fg )                        (4)

.

Таким образом, из экспериментальных данных Ap и T _g можно определить f. В таблице приведены полученные таким образом значения f g для неорганических стекол и аморфных полимеров [5]. Беломестных и Теслева [6] недавно предложили соотношение

Y D =

3 _|±Щ| 212 — 3р )

которое позволяет оценить параметр Грюнайзена Y D из данных о коэффициенте Пуассона р Примечательно то, что формула Беломестных-Теслевой (5) находится в согласии с уравнением Грюнайзена [6, 7].

В таблице приведены значения y d , рассчитанные по формуле (5). Обращает внимание согласованное изменение величин f_g и y d при переходе от одних стекол к другим: с ростом y d закономерно увеличивается и f g .

Из общих соображений следует ожидать линейной зависимости f g от y d : чем сильнее выражен ангармонизм колебаний решетки, тем больше должен быть флуктуационный объем. В самом деле, у исследованных стекол и аморфных полимеров наблюдается линейная корреляция между долей флуктуационного объема f g и параметром Грюнайзена y d (рис.). По отношению к зависимости f g от y d рассмотренные стеклообразные системы делятся на три группы (табл. и рис.).

Таблица.

Коэффициент Пуассона µ , коэффициенты объемного теплового расширения β g , β l , температура стеклования T g , доля флуктуационного объема f g при T g , параметр Грюнайзена γ D (использованы данные [5])

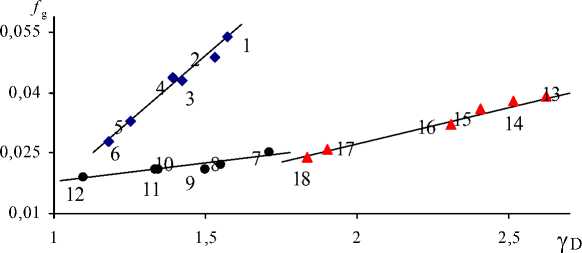
Рис. Зависимость доли флуктуационного объема f g от параметра Грюнайзена y d - Номера точек соответствуют номерам стекол в табл.

Можно попытаться обосновать этот факт, если воспользуемся соотношением [4]

Ар T g =

( 3 RT, )

—- Iyo

D

V V J

где В – изотермический модуль объемного сжатия.

В равенстве (4) в первом приближении можно принять ln(1/ f _;) ~ 3 (табл.), тогда из выражений (4) и

получим

f g

V BV J^y D

Стекло Ц pg-106    1 в i -106 т Tg, К Ав Tg fg Yd ln(1/fg) 1/град 1 Тяжелый флинт SF64 0.264 29.3 206 851 0.150 0.054 1.57 2.9 2 Флинтглас F51 0.257 32.7 240 688 0.142 0.049 1.53 3.0 3 Тяжелый флинт SF16 0.252 27.9 208 716 0.129 0.043 1.42 3.1 4 Флинтглас F2 0.225 25.9 213 705 0.131 0.044 1.39 3.1 5 Стекло для спаев с коваром 8250 0.19 15.2 157 763 0.108 0.033 1.25 3.4 6 Стекло Дуран-50 0.17 11.3 132 803 0.097 0.028 1.18 3.6 7 CS2O-3B2O3 0.29 43.0 173 693 0.090 0.025 1.71 3.7 8 Телевизионный экран 8209 0.26 30.3 136 785 0.083 0.022 1.55 3.8 9 Телевизионная трубка 8198 0.25 28.9 142 703 0.079 0.021 1.50 3.9 10 Na2O-3B2O3 0.215 24.7 140 693 0.080 0.021 1.34 3.9 11 Стекло Керан 8558 0.213 14.8 96 948 0.077 0.020 1.34 3.9 12 Li2O-3B2O3 0.145 13.2 116 693 0.071 0.019 1.10 4.0 13 Полиакрилат 0.40 220 545 378 0.123 0.039 2.62 3.2 14 Поливинилацетат 0.39 266 664 301 0.120 0.038 2.51 3.2 15 Поливинилхлорид 0.38 200 525 354 0.115 0.036 2.41 3.3 16 Полистирол 0.37 169 459 370 0.107 0.032 2.31 3.4 17 Полибутадиен 0.32 195 677 189 0.091 0.026 1.90 3.6 18 Полиизопрен 0.31 158 593 200 0.087 0.024 1.84 3.7 обозначения стекол по каталогу фирмы "Шотт" [5].

У стекол одного класса температура стеклования оказывается пропорциональной модулю упругости: T _g ~ B [8, 9]. Поэтому в первом приближенно можно принять

RT g ----~ const

.

BV

Из приведенных соображений следует ожидать линейную корреляцию между f g и y d (рис.).

Таким образом, между долей флуктуационного объема при температуре стеклования и параметром Грюнайзена стеклообразных систем имеет место вполне определенная взаимосвязь, что согласуется с моделью возбужденного состояния.