Фокусировка цилиндрических векторных пучков дробных порядков

Цилиндрические векторные пучки (ЦВП) получили в настоящее время широкое распространение благодаря уникальным свойствам, проявляемым при острой фокусировке. В частности, с помощью цилиндрических векторных пучков можно получать фокусные пятна с размерами меньше скалярного дифракционного предела [1, 2], фокусы с большой глубиной – оптические иглы [3, 4], световые туннели [5, 6], цепочки фокусов [7– 10] и т.д. Стоит, однако, отметить, что похожие манипуляции с формой фокусного пятна можно делать и без привлечения ЦВП [11].

Поляризация в каждой точке ЦВП линейна, однако ее направление меняется непрерывно, совершая один или несколько оборотов при изменении азимутального угла от 0 до 2π. Большая часть работ (например, ранее отмеченные [1, 3–9]) посвящена изучению ЦВП, в которых поляризация совершает только один оборот – это радиально-поляризованные пучки, в которых поляризация направлена вдоль радиуса, или азимутально-поляризованные пучки, в которых она, соответственно, направлена перпендикулярно радиусу. Однако известны работы, в которых исследуется поведение ЦВП высоких порядков, т.е. пучков, в которых направление поляризации совершает несколько оборотов [12–18]. Большое распространение получило также изучение гибридных векторных пучков [19] – пучков, в которых периодически меняется не только направление поляризации, но и фаза. При этом может меняться как фаза волнового фронта пучка – тогда можно получать пучки, обладающие одновременно сингулярностью фазы и поляризации [18, 20], так и разница фаз между компонентами вектора напряженности электрического поля в разложении по базису декартовой или цилиндрической системы координат, ось z которой направлена вдоль оси распространения пучка – тогда в сечении полученных пучков будет происходить изменение поляризации с линейной на круговую и обратно [21 – 23]. Ранее было показано [24–27], что для ЦВП высоких порядков в области фокуса наблюдаются области, в которых проекция вектора Пойнтинга на оптическую ось приобретает отрицательные значения, а если порядок пучка равен двум, то такая область располагается на оптической оси. Отметим также, что обратный поток энергии можно получить и не прибегая к ЦВП [28].

Одним из способов получения цилиндрических векторных пучков является получение секторных ЦВП с помощью полуволновых пластинок [1, 29– 32], нелинейных оптических кристаллов [33], поляризаторов [34] и субволновых решеток [35–37]. Ранее нами исследовалось влияние количества секторов на результаты фокусировки [38] и было показано, что уже для количества секторов, равного шести, отличия с фокусировкой пучка, в котором поляризация изменяется непрерывно, становятся невелики. Однако ранее не поднимался вопрос, какими будут результаты фокусировки, если направление поляризации в различных секторах будет отличаться от запланированного (радиального или азимутального) – поляризация будет «перекручена» или «недокручена» до целого количества оборотов, к примеру, из-за технологических ошибок в изготовлении секторного элемента.

В данной работе с помощью формул Ричардса– Вольфа моделировалась фокусировка цилиндрического векторного пучка с длиной волны 532 нм и дробным порядком плоской дифракционной линзой с числовой апертурой NA=0,95. Было проведено две серии моделирований: в первой исследовались пучки с дробными порядками от нуля до единицы. Т.е. был осуществлен переход от линейной поляризации к азимутальной. Во втором моделировании исследовалось влияние отклонения порядка пучка от m =2 (т.е. случая, когда обратный поток наблюдается в центре фокусного пятна).

Было показано, что при целых значениях порядка пучка поперечные компоненты вектора Пойнтинга равны нулю, а при дробных значениях – нет. При дробных значениях порядка пучка, изменяющихся от нуля до единицы, наблюдается два ярко выраженных центра с координатами x =0 и y =±0,1 мкм, вокруг которых закручен поперечный поток в области фокуса. Вокруг верхнего центра поток вращается по часовой стрелке, а вокруг нижнего – против часовой. При увеличении порядка пучка больше единицы таких ярко выраженных центров вращения поперечного потока становится больше. Также было показано, что обратный поток сохраняется в центре пятна даже при значительном отклонении порядка пучка от m =2 – вплоть до m = 1,55.

Моделирование

В данной работе исследования осуществлялись с помощью формул Ричардса–Вольфа [39]

•Г ^a max 2 п

U ( р , y , z ) = - f f f B ( 0 , ф ) T ( 0 ) P ( 0 , ф ) х

^ 0 0

х exp { ik [p sin 0 cos ( ф - y ) + z cos Oj } sin 0 d 0 d ф ,

где U(ρ, ψ, z) – напряжённость электрического или магнитного поля, B (θ, φ) – электрическое или магнитное поле на входе широкоапертурной системы в коор- динатах выходного зрачка (θ – полярный угол, φ – азимутальный), T (θ) – функция аподизации линзы, f – фокусное расстояние, k = 2п / X - волновое число, X -длина волны (в моделировании считалась равной 532 нм), αmax – максимальный полярный угол, определяемый числовой апертурой линзы (NA=sinαmax), P (9, ф) - вектор поляризации, для напряжённости электрического и магнитного полей имеющий вид:

P ( 0 , ф) =

1 + cos2 ф( cos 0-1) sin ф cos ф( cos 0-1) - sin 0 cos ф a (0, ф) +

sin ф cos ф ( cos 0- 1 )

1 + sin² ф ( cos 0- 1 ) I b ( 0 , ф ) , - sin 0 sin ф

где a (θ, φ) и b (θ, φ) – функции, описывающие состояние поляризации x - и y -компонент напряжённостей фокусируемого пучка.

Для светового поля с цилиндрической поляризацией m -го порядка азимутального вида вектора Джонса будут иметь вид:

E ( 0 , Ф ) =

^ a ( 0 , ф ) " _v ь ( 0 , ф )_?

'" sin ⁽ m ф ) " _v cos ( m ф ) ^

для напряжённости электрического поля и

H ( 0 , Ф )

^ a ( 0 , ф)^ v b ( 0 , ф)>

'^{- cos ( m ф}Г _v - sin ( m ф )

для напряжённости магнитного поля. Если положить в формулах (3), (4) m = 1, то они будут описывать обычный азимутально-поляризованный свет, а для m =0 – линейно-поляризованный свет, направленный вдоль оси y .

Фокусировка цилиндрических векторных пучков с порядком от нуля до единицы

Рассмотрим фокусировку пучков с дробным порядком, изменяющимся от нуля (линейно-поляризованный свет) до единицы (азимутальная поляризация) с шагом Δ m = 0,25. На рис. 1 показано направление поляризации для дробных значений m : 0,25, 0,5 и 0,75. Моделирование осуществлялось с помощью самостоятельно написанного программного обеспечения в среде Matlab. Корректность работы разработанного ПО подтверждалась в ранних работах авторов [25] путем сравнения полученных результатов с результатами, полученными в программном обеспечении RSoft Fullwave. На рис. 2 показано изменение суммарной интенсивности и отдельных компонент интенсивности для этого случая, а на рис. 3 аналогично – компонент вектора Пойнтинга.

Из рис. 2 и 3 видно, что при изменении порядка пучка m от нуля до единицы происходит изменение распределения интенсивности с эллиптичного к кольцевому, при этом промежуточные состояния имеют вид наклоненных эллипсов. Наклон и уширение пятна в одном из направлений при порядках пучка m , близких к нулю, обеспечивается продольной составляющей интенсивности, а при m , близком к единице, – поперечными составляющими.

т=0,25

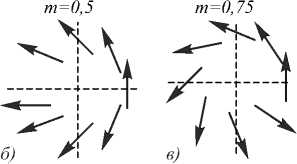
Рис. 1. Направление поляризации в ЦВП дробного порядка m: m=0,25 (а), m=0,5 (б), m=0,75 (в)

т=0

0,5

-0,5

I О

V, МКМ

-0.5 0 0,5

у, мкм

т=0,25

0,5

О

-0.5

-0,5 0 0.5

т=0,5

т=0,75

т=1

V. - МКМ

V, МКМ

0,5

0,5

-0.5 0 0,5

-0.5 0^ 0,5^

-0,5      0,5^

0.5

-0.5

к о

-0,5 0 0,5

у, .МКМ

0,5

О

-0.5

-0.5 0 0,5

X, мкм

о

-0,5

-0.5 0 0.5 л; .мкл;

о

-0,5

-0,5 0 0.5

0,5

-0,5

1х О

1,0 0.8

0.6

0,4

0,2

-0,5 0 0,5

у, -МКМ

О

-0,5

-0.5 0 0,5

V, Л//С-У

0.5

о

-0,5 0 0.5

0,5

о

-0.5 О

у. л,кл.

о

-0,5

-0.5 0^ 0,5"

0,5

1у о

-0,5

-0.5 0 0,5

V, МКМ

0,5

о

-0,5 0 0.5

X, мкм

-0,5

-0,5

-0.5 0^ 0,5^

-0,5 0 0.5

у. Л1КЛ1

0,5

о

-0.5 0 0,5

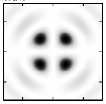
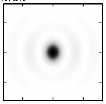
Рис. 2. Распределение суммарной интенсивности I и отдельных составляющих интенсивности Iz, Ix и Iy при фокусировке ЦВП различных порядков: m = 0 (линейная поляризация), m = 0,25, m = 0,5, m = 0,75 и m = 1 (азимутальная поляризация)

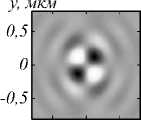
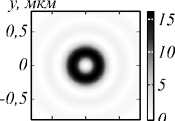
У продольной компоненты вектора Пойнтинга форма распределения меняется с круговой на кольцевую (при m = 0,75 распределение уже имеет вид асимметричного кольца), но промежуточные эллипсы не наклонены, а ориентированы вдоль оси y (направления поляризации при m =0). При целых значениях порядка пучка поперечные компоненты вектора Пойнтинга равны нулю, а при дробных значениях – нет. Наблюдается два ярко выраженных центра с координатами x =0 и y =±0,1 мкм, вокруг которых закручен поперечный поток в области фокуса. Вокруг верхнего центра поток вращается по часовой стрелке, а вокруг нижнего – против часовой. Можно сказать, что траектория поперечного потока энергии представляет собой цифру «восемь» (нижние строчки рис. 3)

Интересно также, что происходит смена формы: у линейной поляризации интенсивность эллиптическая, а продольный поток энергии – круглый, а у пучка с порядком m =0,5 наоборот, интенсивность почти круглая, а продольный поток – эллиптический. Отметим, что при фокусировке оптического вихря с азимутальной поляризацией (порядок пучка m = 1, топо- логический заряд вихря n = 1) также наблюдается круглое пятно. Размеры фокусных пятен для этих трех случаев приведены в табл. 1. Точность полученных численных значений проверялась с помощью уменьшения шага разбиения обсчитываемой области. Шаг уменьшался до тех пор, пока не обеспечилась точность полученных значений диаметров фокусных пятен до трех знаков после запятой.

Из сравнения значений интенсивности в табл. 1 видно, что наименьшее фокусное пятно наблюдается при фокусировке азимутально-поляризованного оптического вихря. А вот сравнивая значения продольной проекции вектора Пойнтинга, следует отметить, что наименьшее значение наблюдается для сфокусированного линейно-поляризованного пучка.

Фокусировка цилиндрических векторных пучков с порядком больше единицы

На рис. 4 показано распределение продольной проекции вектора Пойнтинга при изменении порядка пучка от 1,5 до 1,9 (т.е. поляризация «недокруче-на» до двух полных оборотов в поперечном сечении пучка).

-Sj

т=0

Sz

-0.5 0 0.5

X. мкм

20 ■ 10

Uo

т=0,25

И мкм

0,5

О

-0,5

-0.5 0 0.5

л. мкм

V. Л1КМ

0.5

О

-0,5

-0,5 0 0,5

X, мкм

V, МКМ

0.5

О

-0,5

-0.5 0 0.5

Л", мкм

-0.5 0 0.5

X. мкм

т=0,75

V, мкм

0,5

О

-0,5

-0.5 0 0.5

л; мкм

т=1

-0,5 0 0,5

л; мкм

10 5 О -5 -10 -15 -20

V, мкм

0,5

О

-0,5

-0,5 0 0,5

X, мкм

V, мкм

0,5

О

-0,5

О

-2

-4

-0.5 0 0.5

Л", мкм

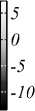
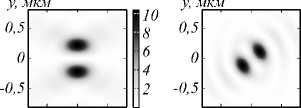
Рис. 3. Распределение отдельных компонент вектора Пойнтинга Sz, Sx и Sy при фокусировке ЦВП различных порядков: m = 0 (линейная поляризация), m = 0,25, m = 0,5, m = 0,75 и m = 1 (азимутальная поляризация)

-0,5 0 0.5

X, мкм

т=1,8

-0,5 0 0,5

X, мкм

-0,5 0 0,5

X, мкм

-0,5 0 0,5

X, мкм

-0,5 0 0.5

X, мкм

Табл. 1. Размеры фокусного пятна по полуспаду интенсивности и продольной проекции вектора Пойнтинга при фокусировке ЦВП различных порядков

	Порядок ЦВП, m	Порядок оптического вихря, n	Ширина пятна по полуспаду интенсивности I = Ix + Iy + Iz		Ширина пятна по полуспаду продольной проекции вектора Пойнтинга Sz
			FWHM x , λ	FWHM y , λ	FWHM x , λ	FWHM y , λ
Азимутально-поляризованный оптический вихрь	1	1	0,460	0,460	0,475	0,475
ЦВП порядка 0,5	0,5	0	0,517	0,484	0,517	0,936
Линейно-поляризованный свет	0	0	0,421	0,751	0,456	0,456

Рис. 4. Распределение продольной компоненты вектора Пойнтинга при фокусировке ЦВП с порядками, изменяющимися от 1,9 до 1,5

Из рис. 4 видно, что при уменьшении порядка m распределение продольной составляющей вектора Пойнтинга Sz приобретает асимметричный вид – кольцо сжимается, а отрицательный поток в центре пропадает. Из рис. 4 также видно, что небольшие отклонения порядка пучка от m =2 не приводят сразу к исчезновению обратного потока энергии на оси. Отрица- тельные значения продольной компоненты в центре фокусного пятна наблюдаются уже при m = 1,55. На рис. 5 показано изменение Sz в центре фокусного пятна. Из рис. 5 видно, что поток на оси положителен при изменении порядка пучка от нуля до единицы. Нулевой для целых порядков пучков m = 1 (азимутально-поляризованный свет), m =3 и m =4. Интересно, что при изменении m от трех до четырех поток на оси положителен. Ранее было показано [24], что, когда m строго равно трем или четырем, поток на оси нулевой, а область обратного потока располагается рядом с оптической осью (имеет вид трубки).

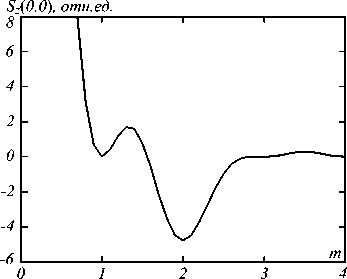
Рис. 5. Величина продольной проекции вектора Пойнтинга Sz(0,0) в центре фокусного пятна при изменении порядка фокусируемого пучка m

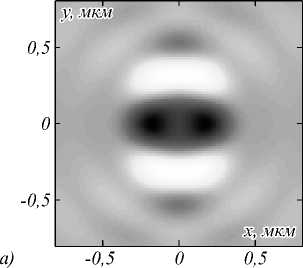
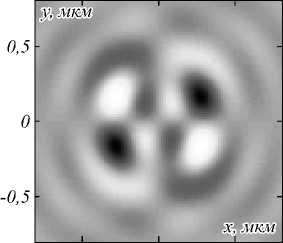
При отклонении порядка пучка m от целого значения поперечные составляющие вектора Пойнтинга S x и S y также становятся ненулевыми, хотя при m = 1 и m =2 они отсутствовали. Поток энергии в плоскости фокуса превращается из ламинарного в турбулентный. В отличие от дробных m ∈ (0,1) выраженных центров вращения поперечного потока становится больше (рис. 6).

Заключение

С помощью формул Ричардса–Вольфа моделировалась фокусировка цилиндрического векторного пучка с длиной волны 532 нм и дробным порядком плоской дифракционной линзой с числовой апертурой NA=0,95. Было проведено две серии моделирований: исследовалось влияние отклонения порядка пучка от m =2 (т.е. случая, когда обратный поток наблюдается в центре фокусного пятна) и исследовались пучки с дробными порядками меньше единицы. Было показано, что:

– при изменении порядка пучка от нуля до единицы распределение интенсивности изменяется с эллиптичного к кольцевому, при этом промежуточные состояния имеют вид наклоненных эллипсов. У продольной компоненты вектора Пойнтинга форма распределения меняется с круговой на кольцевую, но промежуточные эллипсы не наклонены;

– при целых значениях порядков пучка поперечные составляющие вектора Пойнтинга равны нулю, при отклонениях порядка пучка от целого значения поток энергии приобретает турбулентный вид. Для порядка пучка от нуля до единицы наблюдается два ярко выраженных центра с координатами x =0 и y =±0,1 мкм, вокруг которых закручен поперечный поток в области фокуса. При увеличении порядка пучка выше единицы таких выраженных центров вращения становится больше;

– небольшие отклонения порядка пучка от m =2 не приводят к исчезновению обратного потока энергии на оси. Отрицательные значения на оси начинаются от m = 1,55.

0,5

О

-0,5

Рис. 6. Составляющие вектора Пойнтинга Sx (а) и Sy (б) в области фокуса при фокусировке пучка с порядком поляризации m = 1,9

б)

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Фокусировка цилиндрических векторных пучков с порядком от нуля до единицы», Российского фонда фундаментальных исследований –грант 18-29-20003 в части «Моделирование», и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение 007-ГЗ/Ч3363/26) в части «Введение».