Фокусировка цилиндрического векторного пучка второго порядка градиентной линзой Микаэляна

Острая фокусировка лазерного излучения (фокусировка света линзами с высокими значениями числовых апертур) в настоящее время активно используется для формирования оптических игл [1–3], световых туннелей [4, 5] и цепочек фокусов [6, 7]. Ранее нами было показано, что при острой фокусировке цилиндрических векторных пучков n -го порядка с вихревой фазой, у которых топологический заряд вихря m превышает порядок пучка на два ( m = n +2), в фокусе вблизи оптической оси можно наблюдать области с обратным потоком энергии [8]. В частности, такие области наблюдаются при фокусировке оптических вихрей с топологическим зарядом 2 [9, 10] и цилиндрических векторных пучков второго порядка [10, 11]. В случае, если фокусировка исследуемых пучков осуществляется линзами с высокой числовой апертурой, величина обратного потока энергии становится сопоставимой величине прямого потока энергии.

Сила, действующая на проводящую рэлеевскую частицу со стороны светового поля, совпадает по направлению с вектором Пойнтинга [12, 13], следовательно, частица, помещённая в область обратного потока, должна двигаться по направлению к источнику излучения. Поэтому на основе обнаруженного эффекта обратного потока энергии возможно создание световых ловушек. В работах [8–11] область обратного потока расположена рядом с областью прямого потока энергии, в то время как для создания световой ловушки две эти области должны быть изолированы друг от друга. Сделать это можно, сфокусировав свет вблизи раздела двух сред (например, стекло/воздух)

таким образом, чтобы область прямого потока энергии была внутри стекла, а область обратного потока – в воздухе. Градиентные линзы, такие как линза Микаэляна [14] (или гиперболическая секансная линза [15, 16]), линза Лунеберга [17], рыбий глаз Максвелла [18], фокусируют свет вблизи раздела двух сред и могут быть использованы для разделения областей прямого и обратного потоков энергии. Отметим здесь также, что, помимо линз с непрерывным изменением показателя преломления, в последнее время активно изучаются их аналоги, в которых изменяется эффективный показатель преломления: фотонно-кристаллические линзы [19–23], линзы, основанные на чередовании слоев различных материалов [24–26], или линзы на основе метаповерхности [27].

В данной работе моделировалась фокусировка цилиндрического векторного пучка второго порядка градиентной линзой Микаэляна с длиной 10 мкм, радиусом 6 мкм и показателем преломления на оси 1,5. Было показано, что линза формирует вблизи своей выходной поверхности область обратного потока энергии. В случае, если длину линзы сделать больше расчётной и снабдить углублением на оси (цилиндрическое углубление имело диметр 0,3 мкм и глубину 0,8 мкм), удаётся локализовать область прямого потока энергии внутри материала линзы, а область с преимущественно обратным потоком энергии вынести в свободное пространство. На основе таких линз представляется возможным создавать световые ловушки нового типа.

Градиентная секансная линза

В данной работе моделировалась фокусировка цилиндрического векторного пучка второго порядка градиентной линзой Микаэляна. Показатель преломления такой линзы изменяется в соответствии с формулой [14]:

E =

- sin ( 2 ^ ) cos ( 2 ф )

n ( r ) = n 0

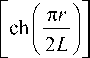
где n 0 – показатель преломления линзы на оси, r – радиальная координата, L – длина линзы, R – радиус. Числовая апертура линзы Микаэляна равна [28]

NA = n 0 - 1 = 72,25 - 1 = 71725 >  1            (2).

В моделировании считалось, что n 0 = 1,5, L = 10 мкм, R =6 мкм из соображений n ( R )= 1 (ранее было продемонстрировано создание метаматериалов с эффективным показателем преломления близким к единице [29, 30]). Моделирование осуществлялось с помощью FDTD-метода, реализованного в программе Fullwave (шаг сетки по пространству 0,015 мкм≈λ / 42).

В качестве освещающего пучка использовался цилиндрический векторный пучок второго порядка, вектор Джонса для него равен где φ – азимутальный угол в цилиндрической системе координат, выбранной таким образом, что ось z совпадает с направлением распространения пучка. Длина волны была равна λ = 0,633 мкм, волновой фронт пучка считался плоским (распределение амплитуды и фазы входного поля было аналогично распределению амплитуды и фазы поля в работе [31] – рис. 1, но было увеличено в ширину до 12 мкм). В дальнейшем полученные в моделировании величины напряжённостей электрического и магнитного полей в фокусе линзы (рис. 2–4) нормировались на максимальные значения величин электрического и магнитного полей освещающего линзу пучка.

Результаты моделирования фокусировки света градиентной секансной линзой

Распределение продольной составляющей вектора Пойтнинга S z в вычисляемой области показано на рис. 2: S z =Re([ E × H *] z ).

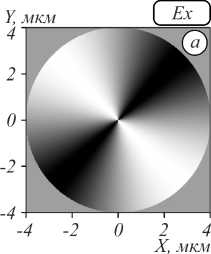
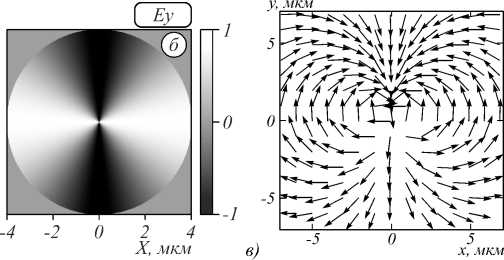
Рис. 1. Распределение входного поля: напряжённость E x (а) и E y (б). Направление поляризации (в)

а)

б)

11,0

10,5

10,0

9,5

9,0

8,5

8,0

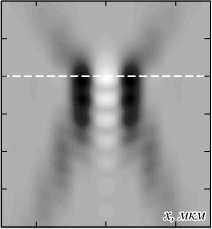
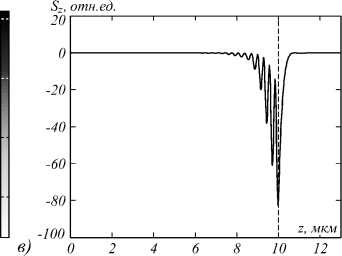
Рис. 2. Распределение продольной составляющей вектора Пойнтинга S z в продольной плоскости xz (а). Увеличенный фрагмент вблизи фокуса (б). Белой пунктирной линией показана граница линзы. Распределение продольной составляющей вектора Пойнтинга S z вдоль оси z (в), чёрной пунктирной линией обозначена граница линзы

Из рис. 2 видно, что вблизи выходной поверхности линзы формируется световой полый цилиндр с диаметром около 400 нм и длиной около 500 нм. Внутри этого цилиндра имеет место обратный поток энергии в виде цилиндра с диаметром около половины длины волны фокусируемого света ~ 0,3 мкм. Максимальные абсолютные значения Sz в областях прямого и обратного потоков сопоставимы по порядку величины, хотя в области прямого потока макси- мум |Sz| и превышает максимум |Sz| в области обратного потока примерно в 1,5 раза. В отличие от обратного потока в фокусе обычной линзы [8–11] область обратного потока на рис. 2 не симметрична вдоль оси распространения света z (рис. 2в).

Градиентная секансная линза с металлизацией

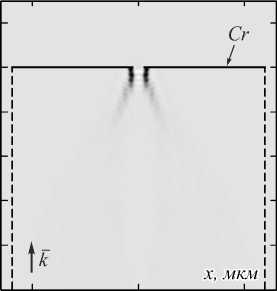
Так же, как и в случае с фокусировкой света в свободном пространстве широкоапертурными линза- ми, область обратного потока окружена областью прямого потока энергии. Изолировать область обратного потока можно, например, покрыв выходную поверхность линзы слоем металла [32]. На рис. 3 показано распределение Sz в расчётной области в случае, если линза покрывается металлом – хромом толщиной 70 нм (на оси оставлено не покрытое металлом отверстие диаметром 0,3 мкм).

Из рис. 3 видно, что область прямого потока энергии в данном случае не выходит за границы линзы, однако и область обратного потока энергии за границу также не выходит.

Градиентная секансная линза с отверстием

Другой способ изолировать область обратного потока энергии (рис. 2) – вырезать отверстие под область обратного потока с одновременным увеличением толщины линзы. Нами была промоделирована линза с высотой на 0,5 мкм выше расчётной и цилиндрическим углублением на оси с диметром 0,3 мкм и высотой 0,8 мкм. Результат фокусировки показан на рис. 4.

Из рис. 4 видно, что таким способом можно изолировать область с максимальным прямым потоком энергии (тёмные области на рис. 4) внутри материала линзы, в то время как в свободном пространстве будет располагаться область с преимущественно обратным потоком энергии. Заметим, что по сравнению с рис. 2 обратный поток уменьшился – на рис. 4 максимум абсолютного значения | S z | в области прямого потока в 4,7 раза больше максимума | S z | в области обратного потока (против 1,5 раз на рис. 2). Также заметим, что цилиндрическое углубление в линзе на рис. 4 работает как открытый резонатор, что приводит к неоднородности обратного потока.

Z, мкм

б

О

-10

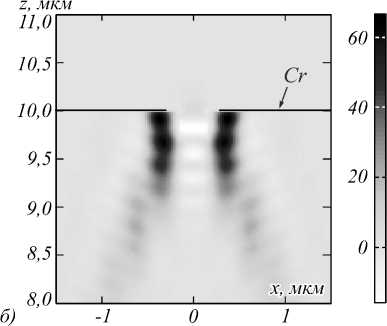
Рис. 3. Распределение продольной составляющей вектора Пойнтинга S z в продольной плоскости xz (а). Увеличенный фрагмент вблизи фокуса (б). Чёрной пунктирной линией показана граница линзы, чёрной сплошной линией – покрытие из хрома

Z, мкм

- 100

б

О

а) 0

-5

О

X, мкм

-20 U

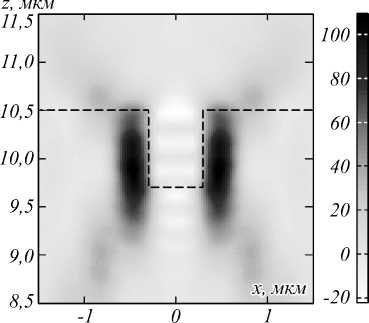
Рис. 4. Распределение продольной составляющей вектора Пойнтинга S z в продольной плоскости xz (а). Увеличенный фрагмент вблизи фокуса (б). Чёрной пунктирной линией показана граница линзы

Заключение

В данной работе нами моделировалась фокусировка цилиндрического векторного пучка второго порядка с длиной волны 633 нм градиентной линзой Микаэляна высотой 10 мкм, радиусом 6 мкм и показателем преломления на оси 1,5. Было показано, что линза формирует вблизи своей выходной поверхности область обратного потока энергии. В случае, если линзу сделать больше расчётной и снабдить углублением на оси, удаётся локализовать область прямого потока энергии внутри материала линзы, а область с преимущественно обратным потоком энергии вынести в свободное пространство. На основе таких линз представляется возможным создавать световые ловушки нового типа.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Градиентная секансная линза», Российского фонда фундаментальных исследований (грант 18-07-01380 в части «Градиентная секансная линза с металлизацией» и грант 18-07-01122 в части «Градиентная секансная линза с отверстием»), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Введение» и в рамках выполнения гранта НШ-6307.2018.8 в части «Заключение».