Фокусировка векторного поля с С-линиями поляризационной сингулярности

Векторные сингулярности, как обобщение скалярных сингулярностей, были рассмотрены J.F. Nye в 1983 году [1]. В [1] линии, в которых поперечные проекции электрического поля равны нулю, названы disclinations (в отличие от скалярных краевых и винтовых дислокаций [2]). Однако в этих работах, как и в работе [3], поляризационные сингулярности исследуются локально, то есть вблизи особых (критических, сингулярных) точек. Актуальным является исследование световых полей с неоднородной поляризацией, у которых в разных точках в сечении пучка имеется разный тип поляризации (линейный, эллиптический или круговой) в глобальном смысле. То есть нахождение топологических зарядов или индексов сингулярности для всего поля целиком. Это актуально потому, что в последнее время растет число работ по генерации и исследованию векторных световых полей с неоднородной поляризацией [4]. Пучки с неоднородной поляризацией можно формировать ин-терферометрически [5], внутри резонатора [6], c помощью q-пластинок [7], метаповерхностей [8, 9], поляризационных призм [10] и модуляторов света [11]. Точки с нулевой интенсивностью, когда не определено направление линейной поляризации, называются

V-точками [3]. Аналогично точки светового поля с неоднородной эллиптической поляризацией, в которых не определено направление главной оси эллипса поляризации, называются C-точками. В этих точках поляризация круговая. Если C-точки лежат на линии, то такая линия называется С-линией [3]. Поляризационные сингулярности характеризуются с помощью индексов сингулярности, которые рассчитываются аналогично топологическому заряду для скалярных световых полей [12]. Индекс поляризационной сингулярности для V-точек называется индексом Пуанка-ре–Хопфа [3] и рассчитывается с помощью параметров Стокса [13 – 15]. А C-точки описываются индексом, который равен числу поворотов на π главной оси эллипса поляризации при обходе С-точки. Индекс Сточки может быть дробным (полуцелым), если за полный оборот эллипс поляризации поворачивается на π нечетное число раз. При переходе через С-линии ось эллипса поляризации скачком поворачивается на π /2. В [16] рассмотрена суперпозиция двух пучков Лагерра–Гаусса с обобщенной векторной поляризацией (то есть у каждого пучка неоднородная линейная поляризация) разного порядка m 1 и m 2 . В перетяжке у суперпозиции таких пучков имеются | m 1 – m 2 | V-точек 1-го порядка, которые при распространении порождают пары C-точек +1 и –1 порядков.

Но в [16] рассматриваются только параксиальные пучки и нет острой фокусировки. В работе [17] рассматриваются C-точки и С-линии (и их преобразование) в одноосном кристалле при осевом и наклонном параксиальном распространении света с круговой поляризацией, которые формируются при разной фазовой задержке между обыкновенным и необыкновенным пучками.

В данной работе мы рассмотрим гибридное векторное световое поле n -го порядка, в котором в зависимости от полярного угла поляризация меняется от линейной до эллиптической и круговой. В этом начальном поле будут только C-линии, число которых равно номеру n . Мы найдем компоненты вектора Стокса для этого поля и покажем, что индекс поляризации этого поля будет полуцелым n /2. С помощью формализма Ричардса–Вольфа [18] мы получим аналитические выражения для проекций вектора напряженности электрического поля в остром фокусе для начального гибридного поля n -го порядка, а также выражения для интенсивности в фокусе. Окажется, что при четном номере n интенсивность обладает определенной симметрией и имеет C-точки в фокусе. То есть мы численно покажем, что С-линии в начальном поле «распадаются» на С-точки в фокусе, которые лежат на тех же линиях. Также мы получим аналитические выражения для проекций вектора Стокса в фокусе, из которых будет следовать, что при нечетном номере n поле в фокусе чисто векторное, состоит из векторов линейной поляризации, имеет несколько V-точек и не имеет C-точек.

1. Начальное гибридное векторное поле с точками поляризационной сингулярности

Рассмотрим гибридное векторное поле n -го порядка, заданное в начальной плоскости двумя поперечными проекциями вектора напряженности электрического поля с вектором Джонса в виде:

1 [ cos n ф E n (Ф) = ^l ■ •

где n - целое число, 0 <  | a | <  1. Из (1) следует, что при n =0 световое поле (1) имеет эллиптическую поляризацию, а при | a | = 1 - круговую поляризацию. При a = 0 поле (1) будет обладать неоднородной линейной поляризацией n -го порядка.

В поле (1) имеются точки с линейной, эллиптической и круговой поляризацией. Точки с круговой поляризацией называются C-точками поляризационной сингулярности, так как в этих точках не определено направление большой оси эллипса поляризации [3]. Топология эллипсов поляризации вокруг C-точки характеризуется индексом Ic, равным целому числу раз изменения на угол π направления большой оси эллипса поляризации при обходе C-точки по замкнутому кон- туру. Для нахождения индекса Ic поля (1) найдем все проекции вектора Стокса [13] S = (S1, S2, S3), где о _ I Ex Р —I Ey\2 С _ 2Re (EXEy)

5 1                       , S 5?                          ,

| E x\ ² + | E y f        E x ]² + E y f

_ 2Im ( E X E y )

5 3 o,

I Ex\ + Ey| где Re и Im – знаки реальной и мнимой части числа. Вектор Стокса, как видно из (2), имеет единичную длину 512 + 522 + 532 — 1. Для поля (1) параметры Стокса из (2) будут иметь вид:

cos 2 n ф-a ²      2sin2 n ф

5 1 — 2--------- z , 5 2 —------- z—,

1 + a ²             1 + a ²

_ 2acosnф

5 з —------z—.

1 + a2

Из (3) следует, что на лучах, исходящих из центра под углами, значение которых легко найти из уравнения 5 ₃=cos n ф = 0, поляризация будет линейной. Под другими углами поляризация будет эллиптической. Круговая поляризация будет при углах φ, удовлетворяющих уравнению 5 3 =1 или cos n ф = ± 1 и a =+1, -1. То есть у поля (1) нет изолированных C-точек, но есть C-линии, при переходе через которые направление большой оси эллипса поляризации меняется скачком на π /2. Одна C-точка эквивалентна винтовой дислокации, а С-линия эквивалентна краевой дислокации. Всего число С-линий в начальном поле (1) будет равно порядку поля n , и они будут совпадать с 2 n лучами, исходящими из центра под углами π m / n , m =0, 1, 2,…2 n.

В работе [3] рассчитывают локальный индекс векторных полей для поляризационных сингулярностей (C-точек), и само векторное поле задается локально вблизи сингулярности. Далее в этой работе мы будем рассчитывать топологический индекс всего векторного поля (1) (глобально), аналогично тому как рассчитывается топологический заряд всего скалярного комплексного вихревого поля по формуле Берри [12]. С этой целью сформируем комплексное поле Стокса по правилу:

5 c — 5 1 + i5 2 . (4)

Для начального векторного поля (1) комплексное поле Стокса (4) будет иметь вид:

5 c — 2

exp ( 2 in ф ) -a ² 1 + a ²

Рассчитаем индекс Стокса σ для поля (5) по формуле Берри [12]:

g — —Im 2 n

2 n

J d ф

d 5 c ( ф ) / дф ⁵c ⁽ф ) .

Подставим в (6) поле Стокса (5), получим:

g = —Im 2 n

2 л j d ф

2 in exp(2 in ф ) exp(2 in ф ) - a ²

2 л

= — I" d ф п 0

( 1 - a ² cos2 n ф )

(1 + a 4 ) - 2 a ² cos2 n ф

Если в (7) положить a ²=1, то о = n , а индекс Сточек и всего поля (1) будет равен Ic = σ /2 = n /2. Индекс Ic может быть полуцелым из-за того, что наклон большей оси эллипса поляризации меняется от 0 до π, а не до 2п. Если в (7) a = 0, то поле (1) становится неоднородным линейно-поляризованным ( S 3 =0) и будет содержать только V-точки (точки неопределенности направления вектора линейной поляризации), индекс Стокса которых (7) будет равен σ = 2 n , а индекс Пуанкаре–Хопфа [3] поля (1) будет в 2 раза меньше П = n . Если 0 <| a |<1, то для расчета индекса Стокса (7) воспользуемся справочным интегралом [19]:

это действительная функция) может быть константой (плоская волна) или в виде Гауссова пучка

|-Y ² sin ² 9

A ( 9 ) = e ^x P I     • ₂n

^ sin ² 9 ₀

где y — постоянная. При a = 0 поле (9) в фокусе c точностью до константы (1/ 2 ) совпадает с полем в фокусе света с радиальной поляризацией n- го порядка [20]:

E x = - ^2 ( 1 0, n cos n ф + 1 2, n - 2 cos( n - 2) ф ) , E y = - i 2 ( 1 0, n sin n ф - 1 2, n - 2 sin( n - 2) ф ) ,

E z = V2 i n 1 1, _n - 1 cos( n - 1) ф .

В поле (11) есть только V-точки поляризационной сингулярности и нет С-точек и С-линий. При n =0 и a = 1 поле (9) совпадает точно c полем в фокусе света с правой круговой поляризацией [21]:

2л cos mx

--------dx =

0 a + b cos x

2n

' V a2 - b2

a ² - b ² (       b

m

- a

С учетом (8) индекс Стокса поля (1) при 0 <| a | < 1 равен σ = 2 n , а индекс Пуанкаре–Хопфа равен η = σ /2 = n . При этом точек с круговой поляризацией не возникает.

E x =--7=( I 0,0 ⁺ e ^{2 ф} I 2,2 ) , 2

^Ey = ^ ^{( 1} 0,0 - e ^{2 ф 1} 2,2 ) ,

Ez = - Ле'ф Iц.

2. Векторное поле с точками поляризационной сингулярности в плоскости острого фокуса

В этом параграфе с помощью формализма Ричардса–Вольфа [18] найдем проекции вектора напряженности электрического поля в плоскости фокуса для начального поля (1). Получим:

Поэтому начальное поле (1) и поле в фокусе (9) можно назвать гибридным, так как в нем есть точки с линейной поляризацией, эллиптической и круговой.

Интенсивность в фокусе для поля (9) будет иметь следующий вид:

i n + 1

E _x = - ^2 ( 1 0, _n cos n ф + 1 2, _n - 2 cos( n - 2) ф ) +

a

+ ^2 1 2,2 Sin2 ф ,

E y = - i 2 ( 1 0, n sin n ф - 1 2, n - 2 sin( n - 2) ф ) +

+ ^2 ( 1 0,0 - 1 2,2 cos2 ф ) ,

E z = V2 i n 1 1, _n - 1 cos( n - 1) ф - i a V2 1 1,1 sin ф ,

I = 2 { 1 12, n ⁺ I 2, n - 2 ^{+ 2} I 0, n I 2, n - 2 ^{cos2( n - 1) ф +} +a ² 1 12,0 +a ² 1 2,2 - 2 a I 0,0 1 2,2 cos2 ф + + 4 1 2-n _n - 1 cos ² ( n - 1) ф + 4 a ² 1 121 sin ² ф -- 2 a cos ^ n -+1 ^ n [ sin n ф ( 1 0,0 1 0, n + 1 2,2 1 2, n - 2 ) - ^{- sin( n - 2) ф} ( I 0,0 I 2, n - 2 ⁺ I 2,2 I 0, n ) ^- - sin ф sin( n - 1) ф 1 1,1 1 1, n - 1 ] } .

где интегралы в (9) имеют вид:

I_v = I ^ f I [ sin ^{v+ 1} ( - )cos ^{3 -v} ( - ) x , J j

x cos ¹/² ( 9 ) A ( 9 ) e k cos ⁸ J _ц ( x ) d 9 ,

где λ – длина волны света, f – фокусное расстояние апланатической системы , x = kr sinθ, J μ ( x ) – функция Бесселя первого рода и NA = sinθ 0 – числовая апертура. Начальная функция амплитуды A (θ) (предположим, что

Выражение для интенсивности (13) достаточно громоздко, но при четном номере n =2 p получим, что cos( n + 1) n /2 = 0 и выражение для интенсивности упрощается:

I n = 2 p = "2 { I 02, n ⁺ I Ini - 2 +

• ^{+ 2} I 0, n I 2, n - 2^{cos2( n - 1) ф+}                          (14)

+a ² 1 0²,0 + a ² 1 22,2 - 2 a I 0,0 1 2,2 cos2 ф +

• + 4 1 12 _n - 1 cos ² ( n - 1) ф + 4 a ² 1 121 sin ² ф } .

Из (14) видно, что интенсивность в центре плоскости фокуса отлична от нуля, так как отлично от нуля

слагаемое а ² I ₀²,₀ . Картина интенсивности будет обладать центральной симметрией 2( n –1)-порядка, так как в (14) входят косинусы от удвоенного угла 2φ и квадраты косинуса и синуса (поэтому при замене φ на φ + π картина интенсивности не изменится). Также картина интенсивности (14) будет иметь 2( n –1) локальных максимумов интенсивности, так как cos2 ( n –1) φ меняет знак 2( n –1) число раз за полный оборот. Для нечетных номеров n = 2 p +1 получим, что cos( n +1) п /2= ± 1, и интенсивность (13) не будет обладать центральной симметрией (так как при φ и φ + π интенсивность будет разная), хотя по-прежнему в центре плоскости фокуса будет максимум интенсивности.

Найдем выражения для проекций вектора Стокса в фокусе. Выражения для проекций вектора Стокса громоздкие, поэтому приведем только проекции для симметричных полей в фокусе, если номер поля четный n =2 p . Воспользуемся другим определением вектора Стокса, у которого 4 проекции, в отличие от вектора Стокса (2):

5 о = \Е_Х |² + \Е„\\s = \Е_Х |² - | Ey |², s ₂ = 2Re ( Е Х * E y ) , s 3 = 2Im ( Е Х E y ) .

Согласно определению (15) для поля (9) ( n =2 p ) получим выражения:

^s 0 = 2 ( I 02, n ⁺ I 22, n — 2 ^{+ 2} I 0, n I 2, n — 2 ^{cos2( n — 1) ф +} +а ² 1 0²,0 + а ² 1 22,2 — 2 а ² 1 0,0 1 2,2 cos2 ф ) ,

Si = 2 (12n cos 2nф +122, l—.

. ₂ cos2( n - 2) ф +

+ 2 1 0, J 2, n — 2 cos 2 ф — а ² 1 0²,0 + 2 а ² 1 0,0 1 2,2 cos2 ф ) ,

-

а ² 1 ₂²,₂ cos4 ф +

^{s 2} = 2 ^{( + 2} I 0. n I 2

sin 2 n ф + 1 2, _{n — 2} sin 2( n — 2) ф +

. ₂ sin 2 ф — а ² 1 ₂²,₂ cos 4 ф +

+2а210,012,2 cos2ф) , s3 = а sin

^— I 2,2 I 2, n — 2 ) ⁺

+ cos( n — 2) ф ( 1 0,0 1 2 n n — 2 — 1 2,2 1 0, n ) ] .

В (16) s 0 , s 1 , s 2 приведены для четных n = 2 p , а s 3 записана для любого n . Это сделано для того, чтобы было видно, что при нечетном номере n =2 p +1 проекция s 3 = S 3 =0, и значит, поле в фокусе не будет иметь C-точек, а будет только векторным, то есть состоящим из векторов линейной поляризации.

Составим из двух проекций поля (16) комплексное поле Стокса:

S c = s i + is 2 = ¹ [ 1 0, n e^{2 in ф} + 1 2, n — 2 e^{2 i ( n — 2) ф} —

^{2 L}                                   (17)

• ^{— а} 2 I 2,2 e ^{41 ф + 2} e ² ' ^ф ( ^а 2 I 0,0 I 2,2 ⁺ I 0, n I 2 nn — 2 ) ^{— а} 2 I 02,0 J .

• 3. Моделирование

Из (17) следует, что топологический заряд вихревого поля Стокса не определен и изменяется по всей плоскости фокуса, так как при больших радиусах r амплитуды при экспонентах будут меняться по величине (то одни больше, то другие, и нельзя определить, какое слагаемое в (17) больше по модулю при больших r ). То есть на некоторых радиусах индекс Стокса поля (17) может быть σ = 2 n , на других радиусах индекс может быть σ = ( n – 2), на других – 4, 2 или 0. Определенно только можно сказать, что вблизи оптической оси отличным от нуля остается только последнее слагаемое в (17), у которого нет вихревой фазы. То есть в центре фокуса при любом n индекс Стокса будет нулевым (σ = 0). Моделирование подтверждает сделанные здесь выводы.

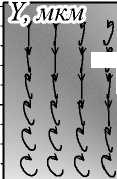
На рис. 1 показано распределение эллипсов поляризации в начальном поле (1) при разных номерах n : 3(a), 2(б), 1(в) и –3(г). Индексы для C-линий полей на рис. 1, рассчитанные по формуле (7) с помощью комплексного поля Стокса, равны Ic = σ / 2 = n / 2: 3 / 2(a), 1(б), 1 / 2(в) и –3 / 2(г). На рис. 1 а видно, что поле (1) с номером n = 3 имеет 3 C-линии, расположенные под углами φ = π m / 3, m = 0, 1, 2. А угол наклона большей оси эллипса поляризации изменяется на π / 2 в каждом из 6 секторов между соседними C-линиями. То есть за полный круг угол наклона большей оси эллипса изменится на 6π / 2 = 3π, то есть индекс поля на рис. 1 а равен Ic = 3π / (2π) = 3 / 2. Аналогично на рис. 1 б поле (1) с номером n = 2 имеет 2 C-линии, лежащие на декартовых осях. При изменении угла φ в одном секторе между двумя С-линиями от 0 до π / 2 угол наклона большей оси эллипса поляризации поворачивается на угол π / 2, тогда за полный оборот вокруг центра угол наклона большей оси эллипса изменится на 4π / 2. То есть индекс для поля на рис. 1 б равен Ic = 2π / (2π) = 1. На рис. 1 в C-линия совпадает с горизонтальной декартовой осью координат. И при изменении угла φ в одном секторе между двумя С-линиями от 0 до π (в верхней полуплоскости) угол наклона большей оси эллипса поляризации поворачивается на угол π / 2, и в нижней полуплоскости угол поворота оси эллипса поляризации также равен π / 2. То есть за полный круг эллипс поляризации повернется на угол π, а индекс сингулярности будет равен Ic = π / (2π) = 1 / 2. Аналогично можно проследить изменения угла поворота главной оси эллипсов поляризации и на последнем рис. 1 г .

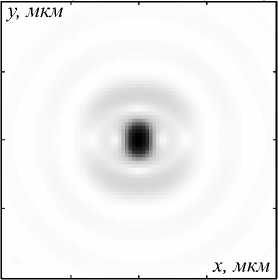
На рис. 2a показана полная интенсивность (негатив) в фокусе поля (1) при а = 1 и n = 2. Расчет производился с помощью формализма Ричардса–Вольфа [18] для длины волны λ =532 нм и числовой апертуры NA = 0,95. На рис. 2б, г показаны амплитуда и фаза комплексного поля Стокса Sc = s1 + is2, рассчитанного с помощью компонент вектора Стокса (16). Из рис. 2а видно, что, как и предсказывает теория (13) и (14), в фокусе картина интенсивности не меняется при замене φ на φ + π, и в центре будет максимум интенсивности. Из рис. 2в видно, что в центре фазы поля Стокса (17) нет сингулярной точки, так как нет изолированного нуля. Два изолированных нуля (точки сингулярности) на рис. 2в с топологическим зарядом 1 каждый видны на вертикальной оси. На рис. 2г стрелками показано распределение эллипсов поляризации в фокусе. На рис. 2д показаны C-точки в фокусе. Все они находятся на декартовых осях, на которых в начальной плоскости были С-линии (рис. 1б). То есть моделирование показывает, что при острой фокусировке C-линии «распадаются» на несколько Сточек, лежащих на тех же линиях. Этот эффект аналогичен эффекту астигматического преобразования краевой дислокации волнового фронта в винтовую дислокацию в скалярной параксиальной оптике [22]. Индексы двух симметричных и ближайших к центру С-точек на горизонтальной декартовой оси равны Ic = ±1 /2, а индексы двух соседних с ними С-точек, расположенных дальше от центра на горизонтальной оси, равны Ic = – 1 /2.

Начальная поляризация, п=3

1 ТУ, мкм                           ‘

О 0 00^$! ID 0000 $ 1) OOO^OZ \ 1 ^ООО$ 1 1! OOC'O ( 1 000$ t

"круговая

Начальная поляризация, п=2

О

^^^^ \ О ОD^ \ D О О О 00000$1$ DOOOOO 0000 D КО ^ ^0<00<0

у ;oooo$ ШОй $ ‘^ont

О

"круговая

$00

t ( $000 D ^OOD D I t$0000Ц t$0000D " $000 0 0 1 t $ 0 0 0 0 5лг1не^ная t мооо ; 1 $000 5 И 0000 D ti $00000

линейная

а)   -1

О           IX, мкм

Начальная поляризация, п=1

1 ТУ, Л1юн

: ^ о и м ^ о и t O'S^nt

•OOO'SHt OO^S 'S 00003$

И 1) 000

1) О ООО

1) О О О О

О 0 000

круговая

ОD0000 О 0 0000

q .0000000^000000

- ODD DO 3

в) -1

о

Единенная

1 Х,мкм

б)1 Х,мкм

Начальная поляризация, п=-3

1 ТУ, мкм                     _ /

• <^0000 1 Г ^0000.5 t$3000^ t$000^ D П$СС0П$00^П

• ■ t I коомоо^ и I

круговая

о

D

О

00000D I D

0000$ ооц ooooo ^^^WO^D^WODO

1 г оос О ооос 0 000^0

ООО$ 'J ^ООО$^ "

О О О О О ^линейная

г) -1

О

1 Х,мкм

Рис. 1. Распределение поляризации (в полутонах и стрелками) в начальном пучке (1) α = 1 для разных порядков n: n=3 (a), 2 (б), 1 (в), –3 (г). Стрелки отражают направление вращения вектора электрического поля, расположение начальной точки эллипса находится в соответствии с фазой поля в данной точке. Наиболее светлые линии – это С-линии

Аналогично на рис. 3 показан результат расчета в фокусе для n =3 (остальные параметры те же, что и на рис. 2). Из рис. 3 а видно, что, как и предсказывает теория (13), картина интенсивности (негатив) в фокусе при нечетном порядке ( n =3) будет асимметричная. Поле в фокусе будет векторным (рис. 3 г ), то есть будет состоять только из линейной поляризации. Это следует из (16), так как при n =2 p +1 получается, что s 3 = S 3 =0. На фазе комплексного поля Стокса (рис. 3 в ) можно увидеть 3 точки фазовой сингулярности с топологическим зарядом +2. А на рис. 3 г можно видеть 3 V-точки, вокруг которых вращаются векторы линейной поляризации. То есть при нечетном порядке n поля (1) С-линии (рис. 1 а ) в начальной плоскости в фокусе преобразуются в несколько V-точек (рис. 3 г ) и все поле в фокусе становится векторным (нет точек с цилиндрической поляризацией).

На рис. 4 показано распределение интенсивности (негатив) в фокусе, обладающее симметрией 4-го порядка относительно декартовых координат (а). Показаны также амплитуда (рис. 4 б ) и фаза (рис. 4 в ) комплексного поля Стокса. На картине фазы поля Стокса видны точки фазовой сингулярности, которые связаны с C-точками (рис. 4 в ). На рис. 4 е показан график индекса Стокса σ от радиуса R окружности с центром в начале координат, вдоль которой рассчитывался набег фазы поля Стокса (17) на картине фазы (рис. 4 в ). Из графика видно, что на разных радиусах R индекс Стокса равен 8, 6, 2, 0, что и предсказывает теория (16).

Из рис. 4г и 4д видно, что С-точки расположены на декартовых осях и на двух диагоналях, там где в начальной плоскости были С-линии. У двух С-точек, расположенных симметрично относительно центра на горизонтальной оси (рис. 4г, д), индекс сингулярно- сти равен 1/2 и топология образует «лимон». При этом поверхность эллипсов поляризации в 3D-

1,0

0,5

О

-0,5

а)

1,0

0,5

О

-0,5     0      0,5    1,0

-0,5

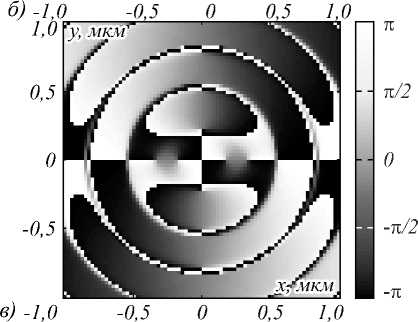
Рис. 2. Интенсивность I = Ix+Iy+Iz (негатив) (а), амплитуда (б) и фаза (в) комплексного поля Стокса (17)

пространстве при обходе такой С-точки образует ленту Мебиуса [23–25].

У, мкм _________________С ^и J

. / / //«»6 /?/^|/^,/<’^-^»^^^'\^'\'1^\\\\ / иЖ V \ \ \

■ //~А / ///z^A ftoooooft f vXXWA А 1 XX

. / -* I I I / / ? А 0»ооб-о«,^м I я\\ А А А / X

/ I I f fl » fftfZ-WW^VA У X А А A —

" I I i < 9 W /V z^---=-^=-*=-^^x X X t

- ШИН / MZ4 <10000 /<^Х\Х V V 6 С t t t M t t / 5 fl о z^o^^O ^xx \ t t t

■ f   1 /» u^/’'^^аа x^x x      e t

. a a a н ti»i j izzx^-^x \ а т - x 1116 e ft a a a m и \ i   i /^^x\ t     a а н e

■ ftft^l H D ft ft ft и ? J^ODti C C ft f-A 4 j I eft

. ее^нпаасуххиАМ/^ссе^-А^Аее

„                  m ft^ceeoi4 Mipe

0 "  ftOMflflAeO O<=^c^-G ft ft ft fr о—о ft ft ft 4 4 i J О ft

. fte b fl fl A e (5СС/» м A XXCiftftM fl fl 4 Oft ee Да fl 4 а е ftf ? м iAi\ftftft'xHflflftft

■ ftftc’-fljAAfmU^oo.^iwt^iMMaft

. ft ft C fl A A A - Г M \\^>^/ / I I \ \ 5 1 1 1 4M!k ft ft ft 5  1 A X /1 A XX*^*-~^/ / J 1 5 11 1

■ ft          1 X X / os^^^^/’ J) » / /1 f \

- t t t t / A VWX/OO^o^OSi^/// / fl/21

r 11 v vxxsv^ppe^/'///11111

-^'tflAAx.i'V X XXV^^^^»®^*^^       I t I I \

- X Г \ X # A,^^^^^^^ (f X 9 I I I I I z X X / A A AWXV ft oc>ooC'ft fl ^z/ / / / I z 1

■ X XX PAAXW^ti A fl fl ^Dr=-zzzzij Wt / . \ X XXI \X*VW>z^-^^^-~*«<'-h’Z’ZZ^ 1«Z / / у X X \ X X / X ^^^r^z^-s»r-=»-=»-ww5>4<>^y?v? Z> 0 z f z f /

г)

д)

-1                           0                            1

।11           X, MKM

при фокусировке светового поля (1) с n=2. Распределение эллиптической поляризации в фокусе (г) (размер кадра – 1×1 мкм) и распределение в фокусе точек с круговой, эллиптической и линейной поляризацией (д)

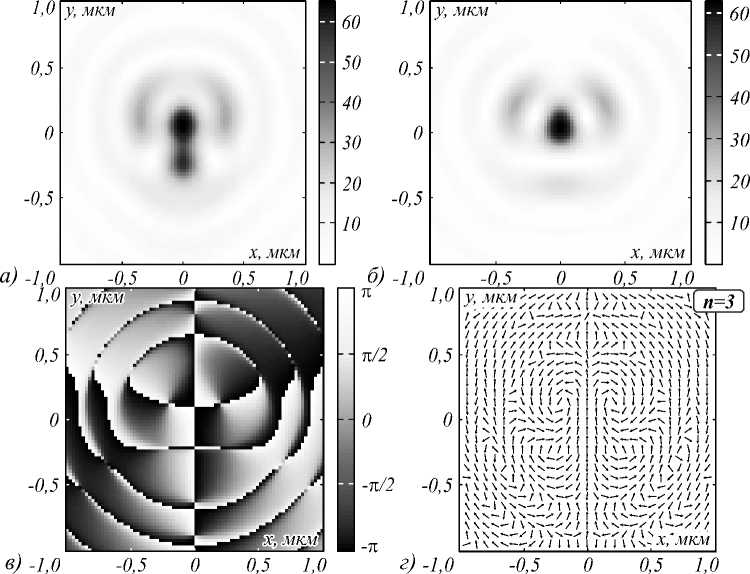
Рис. 3. Интенсивность I = Ix + Iy + Iz (негатив) (а), амплитуда (б) и фаза (в) комплексного поля Стокса (17) при фокусировке светового поля (1) с n = 3. Распределение направлений векторов линейной поляризации в фокусе (г)

а)

1,0

0,5

О

-0,5

-1,0

0      0,5    1,0

У, мкм

M-----

в) -1,0

г) -1,0

11 / / О 1 № «'«'Х

I I I I I I

^ GG »OG t t^ t r t1J

I (f /^—~Xfi I /G^ 1 f r^-^s.XVU\ A \ f / //^nG(\il il C C CCo^xW V Ии f / 1 I C00^ ^ \ It / I C 0 G ^ \ \ \ 1 и И

gchh мссоъд

1) ТйХ’И 9 t?^ t

e'^f)

1 I

l t

ti^oo/^^^o j

j j/z>oo^v i И И J HV n хе,/ И И lj1llX^c»/M\ I 1 \\XGOcS?

V kVS^cf С И1 I

^•ООТ

X/ f П G а t 11 CYClO^Z

\ 111

1  1t t tt

X^ot^ If D Z / / GO b 4✓///.

4N'^0^ X^’^'t \ »t fi Si ^ ^X^^GGC/tZ^// J SHI G—-^^

е) 0

0,2       0,4       0,6       0,8      1,1

д)    круговая

линейная

Рис. 4. Интенсивность I = Ix + Iy + Iz (негатив) (а), амплитуда (б) и фаза (в) комплексного поля Стокса (17)

при фокусировке светового поля (1) с n = 4. Индекс Стокса σ в зависимости от радиуса R окружности с центром в начале координат, вдоль которой рассчитывался набег фазы поля Стокса (г), распределение в фокусе точек с круговой, эллиптической и линейной поляризацией (г) и распределение эллиптической поляризации в фокус, показанной графически (д) (размер кадра 1×1 мкм)

У, мкм

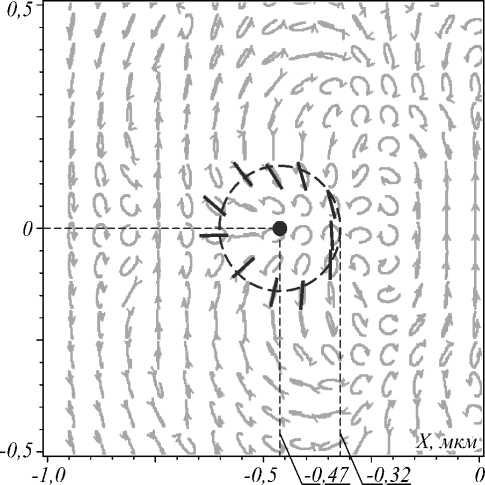
Рис. 5. Эллипсы поляризации части поля в фокусе, показанной на рис. 4е, в координатах (–1 мкм < x < 0; – 0,5 мкм < y < 0,5 мкм) и C-точка с индексом Ic = 1 / 2 и координатами (– 0,47 мкм; 0) (чёрная точка), вокруг которой чёрными отрезками показаны большие оси эллипсов поляризации с центрами на окружности радиусом 0,15 мкм

На рис. 5 более детально показана окрестность одной из C-точек (черная жирная точка на рис. 5) и показан характерный наклон (топология типа «лимон») большой оси эллипсов поляризации, лежащих на окружности, проведенной вокруг С-точки. Видно, что оси эллипсов поляризации за оборот повернулись на угол π, то есть индекс C-точки равен 1 /2.

Заключение

В работе теоретически и численно исследовано гибридное векторное световое поле n-го порядка и его острая фокусировка апланатической системой. Начальное гибридное векторное световое поле в зависимости от полярного угла меняет поляризацию от линейной до эллиптической и круговой. В этом поле имеются C-линии, число которых равно номеру n. Они идут от центра по 2n лучам. Получены выражения для компонент вектора Стокса для этого поля, и показано, что индекс поляризационной сингулярности этого гибридного светового поля равен n /2. С помощью формализма Ричардса–Вольфа получены аналитические выражения для проекций вектора напряженности электрического поля в остром фокусе, а также выражения для интенсивности. Показано, что при четном номере n интенсивность обладает симметрией n-го порядка и имеет C-точки, которые лежат на тех же линиях, которые были С-линиями в начальном поле. Получены аналитические выражения для проекций вектора Стокса в фокусе, из которых следует, что при нечетном номере n поле в фокусе чисто векторное и имеет несколько V-точек и не имеет C-точек.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-2920003) в части «Начальное векторное поле с точками поляризационной сингулярности», Российского научного фонда (грант 18-19-00595) в части «Векторное поле с точками поляризационной сингулярности в плоскости острого фокуса», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Моделирование».