Formal Verification of NTRUEncrypt Scheme
Автор: Gholam Reza Moghissi, Ali Payandeh
Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis
Статья в выпуске: 4 vol.8, 2016 года.
Бесплатный доступ
In this paper we explore a mechanized verification of the NTRUEncrypt scheme, with the formal proof system Isabelle/HOL. More precisely, the functional correctness of this algorithm, in its reduced form, is formally verified with computer support. We show that this scheme is correct what is a necessary condition for the usefulness of any cryptographic encryption scheme. Besides, we present a convenient and application specific formalization of the NTRUEncrypt scheme in the Isabelle/HOL system that can be used in further study around the functional and security analysis of NTRUEncrypt family.
Public key encryption, Lattice, NTRUEncrypt, Formal proof system, Higher order logic, Formal verification, Isabelle/HOL, Theorem proving, Proof assistant
Короткий адрес: https://sciup.org/15011518
IDR: 15011518
Текст научной статьи Formal Verification of NTRUEncrypt Scheme
Formal proof systems are a useful approach in the area of verification. Formal and computer verification augment the traditional concept of software engineering by providing techniques that guarantee trustiness as well as correctness of software systems in a mathematical way. There are many possible applications of formal verification like automotive, medical technology, information technology (software/hardware security, network, cryptography and protocol) and so on. Some of the researches around with formal verification of cryptographic functions, such as Formal Analysis of a Public-Key Algorithm (functional verification and computational security of rabbin encryption and digital signature scheme)[4], Formal Proof for the Correctness of RSA-PSS (functional verification of probabilistic signature scheme RSA-PSS)[20], A Computer Proven Application of the Discrete Logarithm Problem [6](from the thesis: Formalizing the DSA Signature Scheme in Isabelle/HOL[5]), Verification of Cryptographic
Primitive SHA-256 [23] and so on, encourage us to formalize and verify the NTRUEncrypt Scheme.
Now a days, because of the challenge of powerful quantum computer, one of the important scheme in the public-key cryptography is NTRUEncrypt function as suitable post quantum encryption scheme[16]. NTRUEncrypt public-key scheme (not fully) relies on the hardness of solving SVP (Shortest Vector Problem which is the problem of finding shortest vector ̂ in the lattice of ℒ as ̂ ∈ℒ) and CVP (Closest Vector Problem which is the problem of finding a vector ̂ ∈ℒ that is closest to a target vector t∈ Rn not belong to lattice ℒ ) in a convolution modular lattice (since security analysis of NTRUEncrypt Scheme not included in this research we don't open them). In this paper, we explore a computer verification for simplified version of the NTRUEncrypt scheme with the formal proof system Isabelle/HOL. More precisely, the functional correctness of this algorithm is formally verified in a simplified version with computer support. Besides, we present a convenient formalization of the NTRUEncrypt scheme in the Isabelle/HOL system that can be used as a framework for further studies on this function. Further Studies in this domain can be followed by the topics such as: computer verification of security properties using a straight-forward computation model in Isabelle/HOL, applying of Isabelle/HOL to the complete version of NTRUEncrypt function, checking the applicability of deferent introduced traditional attacks on the NTRUEncrypt scheme, checking the applicability of quantum attacks on the NTRUEncrypt scheme (which need to formalize the necessary quantum primitives and theorems in Isabelle/HOL), and so on.
The NTRUEncrypt public key cryptosystem, also known as the NTRU encryption algorithm[1], is a latticebased alternative to RSA and ECC which is based on the shortest vector problem (SVP) in a lattice (which is known not to be breakable using quantum computers). The first version of the system, which was simply called NTRU, was developed around 1996 by three mathematicians (J. Hoffstein, J.Pipher and J.H. Silverman)[1]. In 1996 these mathematicians together with D. Lieman founded the NTRU Cryptosystems, Inc. and were given a patent on the cryptosystem. Now the system is fully accepted to IEEE P1363 standards under the specifications for lattice-based public-key cryptography (IEEE P1363.1)[12, 16]. Because of the speed of NTRUEncrypt public key cryptosystem and its low memory use, it can be used in applications such as mobile devices, Smart-cards and so on. In April 2011, NTRUEncrypt was accepted as a X9.98 Standard, for use in the financial services industry[16].
This paper is organized as follows: We start in Chapter 2 with a description of the used formal proof system. In
Chapter 3 we explore the mathematical background of NTRUEncrypt scheme. In Chapter 4 we present a main formalization of the NTRUEncrypt Algorithm, and in chapter 5 we introduced the issues related to verification of the NTRUEncrypt Algorithm (which include some formalization of scheme). At the end, in Chapter 5 some conclusions, as well as some comments on future works are given.
-
II. Isabelle Formal Proof System
Isabelle is a generic system for implementing logical formalisms which invented at Cambridge University and TU Munich[9]. Isabelle/HOL is the specialization of Isabelle for HOL (which abbreviates Higher-Order Logic), and can be applied to several logics[9]. Other logics distributed with Isabelle include the usual first-order logic (FOL) or LCF (which is a version of Scotts logic for computable functions). Isabelle/HOL allows to turn executable specifications directly into codes in SML, OCaml, Haskell, and Scala[22].
Isabelle is also often referred to as a “Proof Assistant” underlining the process of alternating automated reasoning with human intervention. Theorem proving with Isabelle is often based on a “human-guided” manipulation of the proof state, where the system itself only executes the given commands and verifies their applicability until finally all subgoals have been proven (e.g. via reduction to already proven lemma). On the other hand there are also strong tools that can be applied to handle (suitable) proofs (or at least considerable parts of it) automatically.
Isabelle comes with a large theory library of formally verified mathematics, including elementary number theory, analysis, algebra, set theory and so on. Using appropriate include commands we may base our (new) theorems upon those in the libraries by referring to them during the proof process wherever they are applicable. More informations about the Isabelle/HOL are given in [7-10, 22].
-
III. NTRU Encryption Scheme
In 1998 Jeffrey Hoffstein, Jill Pipher, and Joseph Silverman introduced NTRU, a new public key cryptosystem in his well known paper[1], "NTRU: A Ring-Based Public Key Cryptosystem" . The original idea for NTRUEncrypt is due to Hoffstein in 1994 and the system was developed by Hoffstein, Pipher, and Silverman during 1994-1996. NTRU features reasonably short key, easily created keys, high speed functions, and low memory requirements.
The encryption procedure of NTRU cryptosystem uses a mixing system based on polynomial algebra and reduction modulo two numbers p and q , while the decryption procedure uses an unmixing system which its validity depends on elementary probability theory[1]. The security of the NTRU public key cryptosystem comes from the interaction of the polynomial mixing system
with the independence of reduction modulo p and q . NTRUEncrypt is in fact a lattice-based public key cryptosystem, because underlying convolution polynomial ring ℤ[ X ]/( XN -1) mod q is Convolution Modular Lattice and security of it also rests on the difficulty of solving CVP and SVP in these lattices.
NTRUEncrypt is a probabilistic cryptosystem, meaning that encryption includes a random element, so each message has many possible encryptions. Also, decryption Process may cause failure such that you can estimate this decryption failure for different centering algorithm (described in subsection 3.4) [3]. It is showed that for a recommended parameter sets, the chance of decryption failure can be less than 2 -100 !
A. NTRU Encryption Notation
NTRU cryptosystem depends on three integer parameters ( П , p , q ) and four set of integer 1 vector with length n (or polynomials of degree n - 1 with integer coefficients): ℒ f, ℒg, ℒr, ℒ m . Vectors belong to each of these four sets, are short (in practice with the entries of +1 , -1 and 0 ), such that have a specific Integer bound2: ℒf = ℒ( dj , d^ -1) , ℒg = ℒ(da , da) , ℒr = ℒ( dT , dr ) and ℒm =ℒ( ^m , ^m) . We assume that gcd ( P , q ) = 1 , q ≫ p and n > 0 . The vector f have an inverse in modulo q (shown by Fq ) and have an inverse in modulo p (shown by Fp ). A vector or polynomial F ∈ ̂ in the ring ̂ = [ X ]/( xn - 1) will be written as[1]:
F =∑i=0 F[Xl=[Fo , Fi,…,F.-i] (1)
We write ⊗ to denote multiplication in ̂ as a cyclic convolution product in 0 ( ri2 ) operations:
F⊗G= ℎ (2)
к n-1
Hk =∑FtGk-t+∑ ^i^n+k-l
1=0 i=k+l
∑ FtGt t+j≡(mod. и)
The ring ̂ allow us to compute F ⊗ G = as[2]:
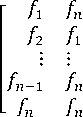
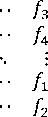
fl 1 г 51 1
∗
⎢⎢ ⋮ ⎥⎥⎢ 9n-l ⎥
⎡ℎ1
⎢⎡ℎ⋮
⎢ℎ
⎣ℎ
In this paper, multiplication of an integer number with a vector showed by " ∙ ", multiplication of an integer number with an integer number showed by " ∗ " and addition of two vectors showed by " ⨁ ".
The width of a polynomial A ( x ) is the difference between its largest coefficients, Max ( A ( x )) =
1 It is arbitrary to select every rings in modulo of an integer number
2 The set of ℒ(d+i, i) contains the vectors that have d+icoefficients of +1 and d^coefficients of -1
max{d0 , CL-^ ,…, ^n-1} and smallest coefficients,
Min (A(x)) = min{d0 , d^,…,dn_i} which is shown as:Widtℎ(A(x)) = Max (A(x)) - Min(A(x)) (4)
B. Key Creation
To create an NTRU keys, two randomly polynomials f and 9 should be selected from ℒf and ℒg , that f have inverse in modulo q and modulo p [1]. We will denote these inverses by Fq and Fp , that is, Fq ⨂ f ≡1 ( mod q ) and Fp ⨂ f ≡1 ( mod p ) , next compute the public key ℎ≡ Fq ⨂ 9 ( mod q ) and private key of the system is ( f , Fp ) .
C. Encryption Process
The plaintext M and additional random bits R are used to select a pair of encoded plaintext polynomials ( r , m ) ∈ ℒr ×ℒm according to a public encoding scheme ℰ . The knowledge of ( Г , m ) allows easy recovery of M and R in practice (also, knowledge of m alone allows easy recovery of M and R , from which r may be recomputed using ℰ )[3]: ℰ( M , R )=( m , r ) and ℰ ([] , m ) = ( R , M ) . To Encrypt the m selected from ℒ m , with randomly chosen polynomial Г from ℒr and using the public key ℎ , we should compute
e≡ ⋅r⨂ ℎ ⨁m(mod q)[1].
D. Decryption Process
To decrypt the encrypted message e by private key, we should perform the following steps[1]:
Because the polynomials r , 9 , f , m are small, their products will in general have low width, thus we can find a correct interval that can reduce a in it so that ℛ( a )= ℛ( a ) ( mod q ) (formula ℛ( a ) refers to Reduced a in the correct interval) and decryption algorithm exactly will recover the m [3, 21]. if we have selected wrong interval, the recovered value will defer from m . A decryption failure will occur if Widt ℎ( p ⋅ r ⨂ 9 ⨁ f ⨂ m )≥ q (referred to gap failure ) or if
Widtℎ(p⋅r⨂9⨁f⨂m) One of the important problem in NTRUEncrypt is the parameter selection to have lowest Decryption failure with most efficient speed and storage. The parameter selection will not discussed here (the same as centering method), we should be able to compute the probability of decryption failure[3]. The likelihood of a decryption failure can be made arbitrarily small, IEEE P1363.1 says in appendix A.4.10[12] that for ternary polynomials with d coefficients of +1 and the same number of -1 , the chance of a decryption failure is given by[13]: (Pro bDecryp £_ℱall( . , ,q)=p( , ).q-? / (5) where p(a, )(c)=n× erfc . / and a (d,n)=√ where erfc is the Gauss error function (as a practical example, for the EES1087EP2 parameter set where N = 1087 , q = 2048 and d = 120 , the failure probability is 5․62 ∗ 10 -78 , which is a bit less than 2 -256 ). We can choose the parameters (d,n,q), so that (Pro bDecryp i_ℱail(d, ,Q ) = 0 in which that, the selected parameters should be have to satisfy following condition[2, 13] to zero this probability (the condition shown below, get from [2]), df < - (6) У 4∗p 2 also, we tested a C language implementation of this condition, and approve that for Q>28,p=3,d^ with the above condition and every values of n, (РТО b^ecyyp f_ℱail(d, ,Q ) become 0 (although lower bound Q >28not mentioned in the [2], the proof not be affected for other more exact bounds of Q from valid references, since in this proof, the selected parameter set be assumed with lowest effect on the proof process). At result, we have the following rule: ((РТО ^yecrypt_ℱail(d, , . ) == 0) → (Widtℎ(а) IV. Formalization of Ntruencrypt Scheme What follows is a summary of the most important steps of the formalization of NTRUEncrypt Scheme in Isabelle/HOL in order to introduce suitable framework of ingredients for NTRUEncrypt algorithm, that make it useful for different functional and security analysis in future. Formalizing of the NTRUEncrypt involved with different concepts that the researches such as, Proving Real-Valued Inequalities by Computation in Isabelle/HOL[11], Proofs of properties of finitedimensional vector spaces using Isabelle/HOL[15], Defining Recursive Functions in Isabelle/HOL[18], and Executable matrix operations on matrices of arbitrary dimensions[19], help us to handle them in the design. Also Isabelle libraries introduced useful Tℎeory files that we can import them in our theory (such as list, vector list, ring and...)[7, 17], but since use of them make the proof process so much harder and more complex, it is decided to use them as least as possible, in other words, most of definitions in this research were tailored to the application and thus enabled short and elegant proofs that are not easily possible with the existing libraries (that is, this thesis just specialized for NTRUEncrypt family). We implement the problem in 3 forms: 1- (just) apply_script lemmas, 2- locales[14] and 3- classes, at the result since the verification of this encryption scheme is very heavy, so we select the well-structured Isabelle Isar proofs with the short step[10] in proving and underlying hierarchy of algebraic classes[7, 14-15] in implementing the operations and lemmas on the convolution modular lattices. Note that type classes are only useful if they are instantiated for several types, but in this research, only integers to be needed. In fact, philosophy of using the type classes in this research is classification of formal primitives to introduce more readability in proof process! The tℎeorem NTRUEncryptVerification is the main theorem of our thesis. Proving of this theorem consists of 8 main steps (main goals), that every main steps may have some sub steps (subgoals). For more readability of proving steps, the assumptions in tℎeorem NTRUEncryptVerification come with "_ " in their names and the lemmas used in the theorem proving come with "_ " in their names. As will be shown in the codes, the "priority order" set by a number that specify the priority, such as (infixl +70), so that big number cause the high priority. Following sample equality shows the priority order of operations in this research (the operator »I that return the i-th integer element of a vector, which is not discussed in this paper): -Ф⨂p∙ℎ ⨁f»5 ∙ ≡ (-((p⨂ (p∙(ℎ -1))) ⨁ ((f»5)∙m)) mod.2 (Я) (8) Note that we omit the unnecessary declarations, definitions, functions and lemmas in this text to make the thesis more convenient to read. A. Basic Primitives Basic concepts in this formalization is the implementation of vectors with same length, addition and multiplication operation on them. The easiest way to achieve this goal is that, preconditions about the length of vectors being omnipresent with the use of unspecified constant definition. So the first basic primitive is declaration of n as a constant, that show length of vectors, consts n∷ʺnat" Since, fixed length condition of vectors is not necessary in addition operation to satisfy correctness of related rules and assumptions in this Tℎeory , we implemented it without length constraint of operands, _ ∷ "int list ⇒ int list⇒ int list( +70)" ℎ "[] + [] = []" | "(x#xs) + [] = X# (xs + [])" | "[] + (У# ys ) =У # ([] + ys)" | "(X#xs) + (У# ys ) = (X+У) # (xs + ys)" Multiplication operation on lattice vectors, against the addition operation, is a complex recursive function that implement matrix vector multiplication (described in section 3.1), and the correctness of it rely on fixed length of vector operands, so we should apply this length constraint on the vectors for multiplication (and other multiplication related operations and rules) with the definition of following function, _ ∷"nat⇒int list⇒int list"wℎere _ " " ^dim _vector 0 [] = []"| _ ^■dim _vector 0 xs = []"| _ _ "W-dim_vector (Sue i) [] = (0 # (W-dim _vector []))"| __ " _ (Sue i) (x# xs) = _ (X# W-dim _vector ^^)" _ This function assume that we reduced a polynomial in the modulo of X11-1, so we just have polynomials of degree n-1 and less (vectors with the length of ≤n) and because all the operations in this Tℎeory have not vector outputs of length > n , so we should only expand the length vectors with the zero entries in the most significant entries up to n entries. Implementation of the function that compute a polynomial modulo of X11-1, have least usefulness and on the other hand heavily increased the proof processes. Since we implement the lattice integer vectors in a hierarchy of classes, so we apply the length constraint on this lattice vectors with the definition of base class vector and inherit from it, class vector = ∷"'a list ⇒'a list" (V [50]) assumes lengtℎrule [simp]:"lengtℎ(VA)=n" instantiation int ∷ begin definition vectorint:: "int list ⇒ int list" wℎere ^def∶"VA ≡ _ "; < instance proof…> end Since Isabelle2009-1, the Isabelle/HOL library already provides a type of lists of length rt′, namely "vec" in HOL/Multivariate_Analysis/Finite_Cartesian_Product with instances for all the required group classes but, as mentioned at the beginning of this section, this thesis just specialized for NTRUEncrypt family to introduce short and elegant proofs (that are not easily possible with the existing libraries). Even if we decided to use the Isabelle/HOL library, the ring classes of this research would have to be instantiated manually, because the multiplication operation is specific to NTRUEncrypt. The ^^cmu^ function implement Matrix vector multiplication with the use of _ (note that inputs of these _ two recursive function is vectors of length n), _ ∷"int vec⇒int vec⇒int"wℎere _ "mnerinult_vec [][] = 0"| " _ ( # ) ( # )=( ∗)+ ( _ ∷ "intvec⇒intvec⇒nat⇒intvec" ℎ " ^Cmult ^ 0 = []"| "recmult A В (Sue i)= ( _ ( ( ( -1)) ))" Since the underlying constructs for operation on convolution modular lattices implement with the hierarchy of algebraic classes, we should define inverse elements of ⨂and ⨁with functions of _ and _ (we define operation of _ in the form of some propositions): _ ∷"int vec⇒int vec"wℎere " _ [] = []" | " _ ( # ) = (- ) # _ " _ ∷ "′ ⇒ ′ " (" - _" [81] 80) _ _ :" _ ≡ _ " _vec ∷"′ ⇒′ " ("_ " [111] 110) We can apply a coefficient for a vector in which that multiply the value of the coefficient with every entries of that vector, definition Scale ∷"int⇒int vec⇒int vec" (infix " ∙ " 100) wℎere "x∙ xs ≡ (op∗X) xs " In this text, we show the operator modulo of an Integer on an integer and modulo of a vector on an integer with the same notation mod (that defined as following function), fun modLtst ∷"int vec⇒int⇒int vec" (infixl "mod" 60) wℎere "[b] mod c = [b mod c]"| "(b#В) mod c = ((b mod c)#(В mod c))" B. Types Declaration/Definition In this subsection we just introduced the Declarations and Definitions that used in formalization and verification: • The annotation vec is just to imply operation on vectors, type_synonym ′a vec = "′a list" • The four variables n,d,p and q used in 3 form nat, int and rat so we implement 2 function nat2 int and nat2 rat to handle type conversions (in this paper each 3 forms of these variables used in same way), consts d∷ " "; consts q∷ " "; consts p∷ " "; • ZERO vector is the unit element of class monoid ipi^s (discussed in subsection classes hierarchy), consts ZERO∷"′a vec" ("0 ") defs ZEROdef∶"ZERO ≡ []" • ONE vector is the unit element of class monoidlmil^ (discussed in subsection classes hierarchy), consts ONE::"′a vec" (" 1 ") defs ONEdef:"ONE ≡ [1]" • Following vectors with the same notation discussed in section 3, consts f∷"int vec" consts g∷"int vec" constsℎ∷"int vec" consts e∷"int vec" consts a∷"int vec" consts m∷"int vec" consts r∷"int vec" consts decryptedm∷"int vec" consts M∷"int vec" consts R∷"int vec" definition Fq∷"int vec"wℎere "Fq = " definition Fp∷"int vec"wℎere "Fp = " • Following boolean variables specify certain conditions in the decryption algorithm and with the same notation discussed in section 3, consts Centringstart∷"bool" consts go-p^^f^e ∷"bool" COnStS WTOPi^^g∷"bool" • Following functions with the same notation discussed in section 3, consts ℰ ∷"int vec × int vec⇒int vec × int vec" constsℰ ∷"int vec × int vec⇒int vec × int vec" constsℛ∷"int vec⇒int vec" • smollcoe^ is set of possible coefficients for f,g,m and r, definition smallcoef ∷"int set"wℎere "smallcoef ={-1, 0, 1}" This research used lots of unspecified constants ( consts ) to simplify the proof steps. Consequently, inside HOL, the theorem holds only for those unspecified values (Only on the meta-level, when one considers the set-theoretic semantics of HOL, one regains generality by considering different models for the constants). C. Classes Hierarchy As mentioned, because of complexity of operations in the convolution modular lattice vectors, we implement these vectors in a classes hierarchy design, as shown in s.1: Fig.1. Diagram of class inheritance for Convolution Modular Lattice The algebraic type class hierarchy introduced in this subsection, is nearly similar to the algebraic class hierarchies distributed with Isabelle/HOL but the main difference is that the class operations here, refer directly to lists of length п , where п is an unspecified constant. This subsection divide in to 14 part that in each part we define a new class, instantiate it on int type and also, sometimes related lemmas mentioned (zero integer in this text showed by 0 and zero vector of length п showed by О , also unit integer showed by 1 and unit vector of the introduced multiplication with length п showed by 1). part1) vector : This class is the base class and other classes inherit the vector length constraints from it (as shown before). part2) р lus : This class inherit from vector , but because the operation ⨁it don't depend on length of vector, so don't apply its length constraint (with V prefix), class plus = + fixes plus ∷"′a vec⇒′a vec⇒′a vec"(infixl "⨁" 70) instantiation int ∷ definition plusint ∷"int vec⇒int vec⇒int vec" wℎere "A⨁В≡ +В" instance ․․end part3) semigroupplus : This class inherit from plus , and apply the rule of right and left associative on the ⨁operation, class semigroupplus = + _ _ :"(x⨁У) ⨁ = x⨁ (7⨁z)" lemma (in semigroupplus ) _ _ : sℎows "(X) ⨁ (У⨁z) = (X⨁У) ⨁z" instantiation int∷ < instance proof…>end part4) monoid l-p^s : This class inherit from semigroupplus, and apply the rule of left unit element on the ⨁operation (note that in this class, rule of _ need to apply length constraint, so we use from this constraint by V prefix), class monoidlplus = + _ :"О⨁ (V A) = (V A)" instantiation int∷ < instance proof…>end Part5) moTtoidplLLS : This class inherit from YTLOTtOld- Ip ^g, and apply the rule of right unit element on the ⨁ operation (note that in this class, rule of _ need to have length constraint, so we use from this constraint by V prefix), class monoidpLus = + _ :"(VA) ⨁О=(V A)" instantiation int∷ < instance proof…>end part6) gToupp^s : This class inherit from TTioTioidpius , and apply the rule of inverse element (and following this rule, groupp ^s satisfy _ _ rule) on the ⨁ operation, class groupplus =+ _: "(-(VA)) ⨁ (VA) =_ " lemma (in groupplus ) "-(V A)=V (-A)" lemma (in groupplus ) _ _ "(VA)⨁(V В)=(VA)⨁(V C)⟷(V В)=(VC)" instantiation int∷ < instance proof…>end part7) _ : This class inherit from дтонрр ^g and apply the rule of commutative on the ⨁operation, _ =+ assumes _ _ _ :"A⨁В= instantiation int ∷ <…> part8) mult : This class inherit from vector , and because the operation ⨂fully depend on length of vector, we apply it's length constraint (with V prefix), class mult = + fixes mult ∷"′a vec⇒′a vec⇒′a vec" (infixl "⨂" 90) instantiation int ∷ definition multint ∷"int vec⇒int vec⇒int vec"wℎere "A⨂ ≡ recmult (rotate (n-1)(rev (VA))) (VB)n" instance ․․end part9) semigroupmult : This class inherit from mult, and apply the rule of right and left associative on the ⨂operation, class semigroupmult =+ _ _: "(A⨂В) ⨂C= ⨂ (В⨂C)" lemma (in semigroupmult) _ _ "A⨂ (В⨂C) = (A⨂В) ⨂C" instantiation int∷ < instance proof…>end part10) mono id 1тиц : This class inherit from semigroupmult, and apply the rule of left unit element on the ⨂ operation, class monoidlmult = + _ :"1⨂A= " ∷ < instance proof…>end part11) monoidmuii : This class inherit from monoidlmuii, and apply the rule of right unit element on the ⨂ operation, class monoidmiM = + _ :"A⨂1= " ∷ < instance proof…>end part12) ring : This class inherit from monoidmult and _ (as shown in Fig. 1) and apply the rule of left distributive and right distributive of ⨂operation on the ⨁operation, class ring = + _ assumes ving^stpibutivity_ "A⨂ (В⨁C) =A⨂В⨁A⨂C" lemma (in ring) :"(A⨁В) ⨂C= ⨂C⨁В⨂C" instantiation int∷ < instance proof…>end part13) commutativering : This class inherit from ring (as shown in Fig. 1) and apply the rule of commutative on the ⨂operation, class commutativering = + _ ∶"A⨂В= ⨂A" instantiation int∷ < instance proof…>end part14) _ (Convolution modular Lattice): _ This class just inherit from commutativering(as shown in Fig. 1), _ = instantiation int ∷ _ ․․ D. Defined functions in _ class _ Encryption/Decryption related functions specifically operate on the _ class that can be defined in the following way: • Encryption method defined as function ℰ^cℳ, definition ( _ )ℰ^Cℳ∷ " int⇒int vec⇒int vec⇒int vec⇒int⇒int vec"wℎere "ℰКСℳp′r′ ℎ′ m′q′≡ (p′∙r′⨂ ℎ′ ⨁m′) mod q′" • Public key compute as function ℋ, definition ( _ ) ℋ:: " ⇒ ⇒ ⇒" ℎ "ℋ Fq′g′q′ = (Fq ′ ⨂g ′) mod q′" • We can compute a (from step 1 of decryption process) as the following function: definition ( ::" ⇒ ⇒" ℎ "Л e′f′≡ e′ ⨂f′ mod q′" • Decryption method defined as function I) ℰcℳ, definition (in corivmoC[lat) 2) ℰCℳ:: " int vec⇒int vec⇒int⇒int vec"wℎere " 2) ℰeℳ Fp ′a′p′ ≡ (Fp ′ ⨂a′) mod p′" • Width method defined as function Widtℎ, definition( _) Widtℎ ∷" ⇒ " ℎ "WidtℎX = ((Max (set X))-(Min (set X)))" V. Verification of Ntru Encryption Scheme What follows is a summary of the most important steps (including necessary lemmas and assumptions) of the formal proof in Isabelle/HOL in order to outline the general course. In the next subsections we described necessary lemmas and assumptions that used in proof of theory NTR UEncryp tyer[^icanon , after we discussed the implementation of Encryption/Decryption scheme (implemented as assumption steps in NTR UEncryp Lveri/ication ) and in last subsection, we discussed briefly the proof steps of NTR UEncryp tyer[^[caiion (note that all the lemmas and assumptions in this section defined in the context of class _ , so we omit the command _ from these lemmas). A. Lemma about the Scale function Function Scale introduced two important lemmas which defined as, _ : "A⨂ (S∙В) = (S∙A) ⨂В" _ :"X∙ A mod. X = " B. Lemma about the lengtℎ constraint As mentioned, the vectors in convolution modular lattice should be in the fixed length n and operator V apply this length constraint on the our vectors, lemma lengtℎ _ "⟦ = ⟧⟹( ℎ =ℎ )" lemma lengtℎ _ "⟦ = ⟧ ⟹ ( =)" lemma lengtℎ _ "⟦( :: ) = ⟧ ⟹ ( ℎ =)" lemma lengtℎ _ :"lengtℎ(VA) =n" _ and for each convolutional modular lattice vectors (f,g, ℎ, e,a,m,r, decrypted_m,m′, Fq , Fp , centered_m,0, 1,M and R) we define this sample lemma (substitute X with the vector name, such as f): lemma lengtℎ _ : :"X= " ℎ " ℎ = " C. Lemma about multiplication inverse element A convolution modular lattice is a ring and each element of this construct may have or have not inverse element so we defined the multiplication inverse operation as the following lemma: _ _ : "⟦∃ ․( = )⟧⟹ (X⨂A mod В = ∧(A⨂X) mod В = )" D. Lemma about the mod operation Since operation on the algebraic constructions that defined by mod operation, introduced longer proof step to handle and work on the propositions, so we defined a set of rules to shortening these proof steps (by guiding the automatic proof tools): ∶ "(A mod X) mod X = " ∶ "(A mod X) ⨂В mod X = ⨂В mod X" ∶ "⟦A= ⟧⟹ (A mod X = )" ∶ "A⨂В mod X=((A mod X) ⨂В) mod X" ∶ "(A⨁В) mod X = ((A mod X) ⨁В) mod X" ∶ "⟦(A mod X)=В⟧⟹(A mod X = )" ∶ "(A mod X) ⨂ (В mod X) mod X = ⨂В mod X" E. Assumptions about n,p,я As be mentioned, we have 3 important integer parameter that should apply some assumptions on them, n_defassm [Intro]:"n>0" ^•Od'U.lclssm2∶"q>p" F. Assumption about Widtℎ of m,r,f,9 For simplicity, according to definition of NTRUEncrypt in [2], and with the assumption of p=3 (SktPassmS), if we assume the following assumptions: _ _ :"m=" _ _ :"r=" _ _ :"f=" _ _ :"9=" the assumptions about Widtℎ of vectors m,r,f,g (that equal to 2), and coefficients of these vectors (that belong to STnallcoef ), can be eliminated (that is the following assumptions be eliminated): _ ∶"set m =" _ ∶"set r =" _ ∶"set f =" _ ∶"set g =" widtℎ _ :"Widtℎ(m)=2" ℎ __ ∶" ℎ( )=2" ℎ __:" ℎ( )=2" widtℎ _ :"Widtℎ(9)=2" G. Assumption about Encoding Scheme Since the encoding and decoding scheme just be declared, so we use the following assumptions to define their operations, Encoding Scheme_ : _ "⟦ℰ(R′, M′)=(r′, m′)⟧⟹ (ℰ ( r′, m′)=(R′ ,м′))" Encodinggc^g^^_ : _ "⟦ℰ(R ′, M′)=(r′, m′)⟧⟹ (ℰ ([i], m′)=(R ′, м′))" H. Assumption about Probability of Decryption Failure We implement the ^P^ObDecrypi _ℱail(d, ,Q ) in Isabelle/HOL, but since the proving process with the operation on rat in this complex function (^ro bDecryp £_ℱail(d, ,Q)) is beyond our thesis[7, 11] and also if we bound the failure probability, it may be required to switch to probabilistic reasoning (in that direction, the theory HOL/Probability/Probability_Mass_Function might be a good starting point). So we assume that parameters d,n and q select from a specific parameter set that zeroed the -E^ob^g^yp^ _ℱail (, , ) value (discussed in subsection 3.4), and consequently add the following assumption (note that if ^ro b^ggyyp / _ℱail(d, ,Q ) be zeroed, we have not 9aPf allure ): Sklpassml∶"q >28" SktPassm2 : "d 4∗2 Sktpassm3 : "p=3" Parameter_: "⟦(q>28); (d< -) ;(P=3)⟧ ∗Pz ⟹(Рто Ь^)есгур / _ℱail(d, ,Q) = 0" Assumptions SktPassml , Skipassm2, Skipassm3 and Parameter_Setassm correspond with phases of passing the gap failure, that is, _ _ and _ , so that proof system pass out this three steps of decryption phases automatically. I. Assumption about the centering method If we have not 9 aPfailure (since we assume that the parameters selected based on Parameter_Setassm cause the Уто b^ggyyp i_ℱail (, , ) be zeroed), the coefficients of Г,9,m,f are small, so the coefficients of p․r⊗9⊕m⊗f will lie in an interval of length less than q . We assume always centring method chooses the appropriate interval, so the polynomial a equals p․r⊗9⊕m⊗f exactly, and not merely modulo q , so the WraPfailurg not be happened. The following assumption have important role in the proof process: centrin gme i^^_ : "⟦ = ; = ⟧⟹ (ℛ a= (p∙r⨂ ℎ ⨁m mod q) ⨂f)" Assumption _ correspond with _ , so that proof system pass out this step of decryption phases automatically. Although, transition from z/q to Z is again assumed instead of proven, but we should note that proving the success of centering method has so complex states! J. Encryption Process We implement the steps of encryption process as assumptions of NTRUETlCryp ^Verification in the following 3 phases (M is original input message): _ :"ℎ = ℋFq gq" _ :"ℰ (R,M) = (r,m)" _ :"e=ℰКС ℳp rℎm q" K. Decryption Process We implement the steps of decryption process as assumptions of NTR UEncryp tverification in the following 7 phases: _ :"a= (dief _ "⟦T^Tob^ggyypt_ℱail(a, ,q)=0⟧⟹(Widtℎ(a)<q)" _ "⟦Widtℎ(a) _ "⟦9 ^Pfailure = (Centringstart =)" _ "⟦Centringstart = (Wrapfailure =)" _ "⟦wrap^a[[ure = (decryptedm = ℰCℳ Fp (ℛ a)p)" _ "ℰ ([ ] , decryptedm)=(R ′, M′)" L. Roadmap of formal verification for NTRUEncrypt Theorem NTRUEncryp tyerification defined in the context of _ . As be mentioned, we used a forward proof steps by Isabelle/Isar structure. We outline proof steps of NT RU Encryp tverification in the following way (note that the following proof road map is not Isabelle/HOL commands and just show outline the proof steps): ⟹ ⟦Skipassmi∧Skipassm2∧Skipassm3∧ _ ⟧ ⟶( _ ) ⟶(Widtℎ(a)<q) ⟶ ⟶ ⟶ ⟶ ⟶ ( _ ( _ ( _ ( _ ( _ ⟦vectorscaIlng_ ⟶ I use ⟹ vectoTscanng_ ∧ lengtℎ _ ∧ _ lengtℎ _ ∧ _ _ lengtℎ _ ∧ _ lengtℎ _ ∧ _ lengtℎrule_lemmaX∧ _ _ ∧тос1ги[еЛ∧TnodTll[e2∧ __ __ ШОС?ги;ез ∧ Ш0С?ги£е4 ∧ Ш0С?ги£е5 ∧ TnodTll[e^ ∧ тОС1ги1е7 ∧ _ _ ∧ __ m°d(!SSm_ _/∧ modassm__ ^odassm _ _ ∧ ™)dassm __ ^odassm _ _ ∧^odassm _modq_ ∧ _ ∧ _ Tingdistributivity_ ∧ Tingdistributivity_ _ ∧ _ _ _ _ _ _ _ _ ∧invers eequaiity∧ _ _ ∧ _ _ ∧ _ _ _ _ ∧lengtℎrule⟧ ⟶( _ ⟹ ⟦ Encoding 5сПете_assml ∧ Encoding 5сПете_ ⟶(M = M') < NTRUEncryptVerification be proved. > As seen in the roadmap of formal verification for NTRUEncrypt, it is not clear what has actually been verified. since theorem NTR UEncryp Lveri/ication assume most of the interesting steps of the scheme being correct (by assumptions introduced). In fact, this research just fully validate the control flow of proposition DℰcℳFp (ℛ a)p == as following way (and other steps validated by some assumptions): Dℰeℳ Fp decryptedm ℛ ⎜⎛ℛ ⎛⏞ ⎞ Л (ℰxeℳp r (⏞ℋ Fq д q)m q) ⎝ ? P ⎠⎠ ⎠ ⎝ ⎝ so that msatisfy condition ℰ ([],m)==(R,M) with the original input message M . Verifying the goal of decryptedm == includes the bellow subgoals which nearly corresponds with the _ (and refered to layer 3 in the table 1 as skeleton of the proof in this research): ⇒ Subgoal 1: "(p∙r⨂ ℎ ⨁ m mod q) ⨂= ((p∙r⨂ℎ⨂f mod q) ⨁ (m⨂f mod q)) mod q" ⇒ Subgoal 2: "(p∙r ⨂ ℎ) ⨂= p∙r ⨂ (ℎ ⨂ f) mod q " ⇒ Subgoal 3: "p∙r ⨂ (ℎ ⨂ f)= (ℎ ⨂f mod q) ⨂p∙ r mod q " ⇒ Subgoal 4: "ℎ ⨂f mod q=(f mod q) ⨂ ℎ mod q" ⇒ Subgoal 5: Fq "(f mod q) ⨂ ((⏞1 mod q) ⨂ (g mod q)) = ((f mod q) ⨂ (f 1 mod q)) ⨂ (g mod q) mod q " ⇒ Subgoal 6: i "((⏞' mod q) ⨂ (f 1 mod q)) ⨂ (g mod q) = g mod q " ⇒ Subgoal 7: "p∙r⨂ ℎ ⨂f mod q = ∙r⨂g mod q " ⇒ Subgoal 8: "ℛ a.=(p∙r⨂ ℎ ⨁m mod q) ⨂f" ⇒ Subgoal 9: "(p∙r⨂ℎ⨂f mod q) ⨁ (m⨂f mod q) = (p∙r⨂ ℎ ⨂f) ⨁ (m⨂f)" ⇒ Subgoal 10: " Fp⨂ ((p∙r⨂ ℎ ⨂f) ⨁ (m⨂f)) = (Fp⨂p∙r⨂ ℎ ⨂f) ⨁ (Fp⨂m⨂f)" ⇒ Subgoal 11: " Fp⨂ ((p∙r⨂ ℎ ⨁m) ⨂f)= (F⨂p∙r⨂ ℎ ⨂f) ⨁ (Fp⨂m⨂f)" ⇒ Subgoal 12: "(Fp⨂p∙r⨂ ℎ ⨂f) ⨁ (Fp⨂m⨂f) = (Fp⨂m⨂f) ⨁ (Fp⨂p∙r⨂ ℎ ⨂f)" ⇒ Subgoal 13: "(Fp ⨂m⨂f) mod p =" ⇒ Subgoal 14: " Fp ⨂ ((p∙r⨂ ℎ ⨂f) ⨁ (m⨂f))= (m⨁ (Fp⨂p∙r⨂ ℎ ⨂f)) mod p" ⇒ Subgoal 15: "m⨁ (Fp ⨂p∙r⨂ ℎ ⨂f)= (Fp⨂p∙r⨂ ℎ ⨂f mod p) ⨁m mod p" ⇒ Subgoal 16: "p∙(r⨂ ℎ ⨂f) mod p =" ⇒ Subgoal 17: " Fp ⨂ (p∙(r⨂ ℎ ⨂f))= Fp⨂ ((p∙(r⨂ ℎ ⨂f)) mod p) mod p" ⇒ Subgoal 18: " Fp⨂ (p∙(r⨂ ℎ ⨂f) mod p) mod p = " ⇒ Subgoal 19: "(m⨁ (Fp ⨂p∙r⨂ ℎ ⨂f)) mod p =" ⇒ Subgoal 20: " Fp ⨂ ((p∙r⨂ ℎ ⨂f)⨁(m⨂f)) mod p =" ⇒ Subgoal 21: " Fp ⨂ ((p∙r⨂ℎ⨁m mod q)⨂f mod q)= Fp⨂ ((p∙r⨂ ℎ ⨂f) ⨁ (m⨂f)) mod p" ⇒ Subgoal 22: "ЪℰeℳFp (ℛ a)p= Note that the main proof steps in the roadmap essentially not be equal to phases of decryption. As an engineering design, it is best to have a high level map to handle the main problem (formal proof of NTRUEncrypt scheme) with less details. A stack of layers in formal proving for NTRUEncrypt scheme be designed in Table 1 (including layers 1 to 4) that classify the proof steps as independent as possible in this research (this layering stack is not essentially an ideal stack for layers of formal proof of NTRUEncrypt scheme and it is possible to have better layering for this scheme): Table 1. Stack of Layers in Formal Proof of NTRUEncrypt Щ Encoding/Decoding layer is last layer in this research to be verified (in this layer, the algorithm of Encoding/Decoding should be selected and fully defined in the formalization and at the end, fully validate the control flow of "£„,„([ ], dertyptedm) = UR M)" for a given message M). [3] Skeleton of the proof is validation of the control flow of "D8CM Fp (Я a) p == m" which is main goal in this research to be verified. Щ Transition from Z/q to Z should be proven as a centering method (which used in decryption phases) chooses the appropriate interval, thus the polynomial p equals "p. г ® g ф m ® f" exactly, and not merely modulo q, so the wrpp jatiure not be happened (in this layer, algorithm of centering method should be selected and fully defined in the formalization and at the end, fully validate control flow of it). [Г! Handling the g pp f a,lure which happen with the probability of PrоЬщестурtы^м) for a given parameter set of (d, n, q) and output p = (Л e f), so that satisfy condition Wtdtd(p) < q with the chance of Ргойу,,,.^tjaiKdm.q'i (it may need to proof process with the operation on rat in the complex function FrobDecrypt_rnii(d,n,q'> or if we bound the failure probability, it may be required to switch to probabilistic reasoning). VI. Conclusions We explored the application of a formal proof system to the simplified version of NTRUEncrypt function introduced in [1]. More precisely, we proved the functional correctness of this algorithm formally with the Isabelle/HOL proof system. In this case, we proved formally that this scheme is correct what is a necessary condition for the usefulness of any cryptographic encryption scheme. A formal analysis with computer support provides a complex, but useful approach to verify the functional correctness of implementations of cryptographic algorithms. This formalization and verification is not a general scheme with high strong design to ideally underlay all further works in this area, but has some main advantages which enumerated as following: • This research can be seen as a start point for further formal proofs in NTRUEncrypt scheme. • Four partially independent layers introduced in this research (as a high level framework for formal verification of NTRUEncrypt scheme) which validated just for layer 3 (Table 1) in this research and other layers can be studied in further works (although the validation of layer 3 in this research can be refine in the further studies). • The computer-proven lemma augment the given database that is basic for many Isabelle theories in the related area. • The functions and other formal primitives which defined/declared in this research can used in the further studies. • Difficulties and problems in the formalization and verification phases enumerated in this paper, also in the most of them, the solution idea introduced and can be resolved easily in the further studies. • An algebraic type class hierarchy introduced in this research which can be used in the further studies. VII. Further Studies As mentioned in section 6 (Conclusion), difficulties and problems in the formalization/verification phases enumerated in the different sections (subsections) of this research, so that, most important of them can be resolved by following further studies: • As the constants are not polymorphic, the generality can equally be expressed inside HOL, e.g., by turning all unspecified constants into parameters of a locale and the resulting development will more usable, because the parameters can be instantiated inside the logic. • Ideally, the algorithms in this research should be defined (rather than axiomatised as is done in this research). • The important properties in this research should be proven under as weak assumptions as possible. • This research restrict the parameters of the encryption algorithm to a small set of values, so generality of this parameter set can be studied to have more usefulness of the formal proof. • Layer 1 of the formal proof (Table 1) which corresponded to Handling the gpp ^ a;iure, can be studied to be verified (as far as possible) in the further studies. • Layer 2 of the formal proof (Table 1) which corresponded to centering method functionality for handling , should be studied to be verified (as far as possible) in the further studies. • Layer 4 of the formal proof (Table 1) which corresponded to Encoding/Decoding functions can be studied to be verified (as far as possible) in the further studies. • A lot of space in this research is spent on reinventing existing libraries (in particular, the algebraic type class hierarchy and vectors of fixed length) to have short and elegant proofs (that are not possible easily with the existing libraries), thus the benefits from all the corollaries and the setup for proof automation that has been developed for the existing primitives in Isabelle/HOL libraries be lost and also extending the area of this proof to be used in other external theorems using the standard Isabelle/HOL libraries, faced with problems, so use the existing libraries as far as possible in the further studies. • This research partially focus on elegance or encapsulating fundamental insights that are adaptable and reusable so these properties should be consider more in further studies.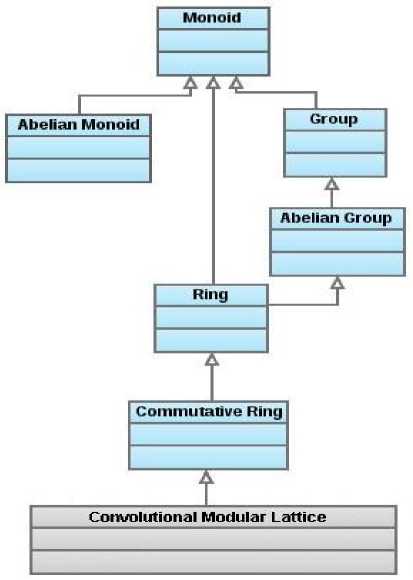
Список литературы Formal Verification of NTRUEncrypt Scheme
- Hoffstein, J., Pipher, J., Silverman, J.H., "NTRU: A ring-based public key cryptosystem", Lecture Notes in Computer Science, 1998.
- Bernstein, D.J., "Post-Quantum Cryptography", Department of Computer Science, University of Illinois at Chicago, 2008.
- Silverman, J.H., Whyte, W., "Estimating decryption failure probabilities for NTRUEncrypt", Technical report, NTRU Cryptosystems, Report #018, version 1, available at http://www.ntru.com, 2003.
- Kaiser, M., Buchmann, J., "Formal Analysis of a Public-Key Algorithm", International Journal of Computer Science 2.2, 2007.
- Kusch, S., Buchmann, J., "Formalizing the DSA Signature Scheme in Isabelle/ HOL", Diplomarbeit, Technische Universit¨at Darmstadt, 2007.
- Kusch, S., Kaiser, M., "A Computer Proven Application of the Discrete Logarithm Problem", International Journal of Computer Science 2.2, 2007.
- Nipkow, T., Paulson, L.C., Wenzel, M., "Isabelle/HOL—a proof assistant for higher-order logic", Lecture Notes in Computer Science, vol. 2283. Springer, 2002. doi:10.1007/3-540-45949-9.
- Nipkow, T., Klein, G., "Concrete Semantics-A Proof Assistant Approach", Springer, 2014.
- Nipkow, T., "Programming and Proving in Isabelle/HOL", http://isabelle.informatik.tu-muenchen.de/, 2012.
- Wenzel, M., "The Isabelle/Isar Reference Manual", TU MÄunchen, MÄunchen, 1999, http://isabelle.in.tum.de/doc/isar-ref.pdf.
- Holzl, J., "Proving Real-Valued Inequalities by Computation in Isabelle/HOL", Diploma thesis, Institut f¨ur Informatik, Technische Universit¨at M¨unchen, 2009.
- "IEEE P1363.1. Public-key cryptographic techniques based on hard problems over lattices", http://grouper.ieee.org/groups/1363/lattPK/index.html, Accessed May 31, 2014.
- Hoffstein, J., Howgrave-Graham, N., Pipher, J., Silverman, J.H., Whyte, W., "Hybrid lattice reduction and meet in the middle resistant parameter selection for ntruencrypt", NTRU Cryptosystems, Inc., Acton, MA, Tech. Rep., 2007.
- Ballarin, C., "Tutorial to locales and locale interpretation", In L. Lambán, A. Romero, and J. Rubio, editors, Contribuciones Científicas en honor de Mirian Andrés Gómez. Servicio de Publicaciones de la Universidad de La Rioja, Logroño, Spain, 2010.
- Mallagaray, J.D., "Proofs of properties of finite-dimensional vector spaces using Isabelle/HOL", Universidad de La Rioja, 2011/2012, http://www.unirioja.es/cu/jodivaso/degree_thesis/.
- Security Innovation, https://www.securityinnovation.com/. Accessed August 9, 2013.
- Nipkow, T., "What's in Main", Isabelle TUM, 2013, http://isabelle.in.tum.de/doc/main.pdf.
- Krauss, A., "Defining Recursive Functions in Isabelle/HOL", Isabelle TUM, 2008, http://isabelle.in.tum.de/documentation.html.
- Sternagel, C., Thiemann, R., "Executable matrix operations on matrices of arbitrary dimensions", Archive of Formal Proofs, 2010.
- Lindenberg, C., Wirt, K., Buchmann, J., "Formal proof for the correctness of RSA-PSS", IACR Cryptology ePrint Archive 2006, 11.
- Silverman, J.H., "An Introduction to the Theory of Lattices and Applications to Cryptography", Computational Number Theory and Applications to Cryptography, University of Wyoming, 2006.
- Isabelle-TUM, https://isabelle.in.tum.de/(2013). Accessed December 05, 2013.
- Appel, A.W., "Verification of a Cryptographic Primitive: SHA-256", ACM Transactions on Programming Languages and Systems (TOPLAS), Princeton University, 2015.


