Формализм решения первой задачи динамики шагающих и колесно-шагающих машин

Шагающая машина (ШМ) – это древовидная система тел с переменной структурой, ветви которой периодически замыкаются на опорную поверхность (ОП) и размыкаются в процессе перехода ноги из опорного состояния в переносное. ШМ обеспечивает перемещение своего корпуса за счет относительных движения тел опорных ног. Во многих областях деятельности человека по сравнению с традиционными транспортными средствами автоматически управляемые ШМ оказываются вне конкуренции. К таким областям относятся: транспортные, грузоподъемные и монтажные операции на сложной местности и в условиях чрезвычайных ситуаций (зоны разрушений, горная местность, откосы дорожного полотна и др.); перемещение при минимальных повреждениях поверхностного слоя земли; перемещение в среде, для которой характерны узкие проходы, спуски, подъемы, выступы и т. п. [1–3].

Использование ног в качестве движителей позволяет повысить профильную проходимость и перемещаться по сильно пересеченной местности. За счет изменения движения ног относительно корпуса ШМ может обеспечить комфортабельное движение своего корпуса при перемещении по поверхности с неровностями, достигающими величины дорожного просвета, и компенсировать деформацию грунта в точках опоры ног. Высокая маневренность и возможность адаптации позволяют использовать ШМ в помещениях, приспособленных для человека (лестничные марши, узкие коридоры с поворотами на 90 градусов, дверные проемы). ШМ способны перемещаться вперед, назад, вбок, совершать повороты и развороты на месте, перемещаться под произвольным углом между направлением движения и продольной осью ШМ [4, 5].

ШМ можно использовать в качестве многоцелевой шасси-платформы, имеющей высокую проходимость и способную доставлять в нужное место и обеспечивать функционирование технологического оборудования, средств обезвреживания мин, доставки на исходную позицию средств ведения боевых действий с танками, вертолетами и другими боевыми единицами противника с максимальной эффективностью и минимальным риском для личного состава армии [6].

В середине 80-х годов прошлого столетия во многих странах приступили к созданию ШМ, предназначенных для ликвидации последствий аварий на АЭС. Они конструировались для целей перемещения в замкнутых пространствах (в помещениях ограниченного объема). Такие ШМ способны протискиваться в проломы, спускаться и подниматься по лестничным маршам, избегать провалов в полу и т. д. При ликвидации последствий крупных техногенных аварий и катастроф возникает потребность проведения ремонтных и спасательных работ, разведки местности и очистки территорий в особо опасных условиях для людей (радиоактивных, токсичных, взрывоопасных средах, под водой, в шахтах, в завалах и др.), в которых колесные и гусеничные автоматически управляемые транспортные средства не работоспособны [7–9].

Одной из ключевых задач при организации движения ШМ по ОП является определение динамических реакций в точках опоры ног. Для заданного движения корпуса и ног реакции в точках опоры определены, как правило, неоднозначно. Эта неопределенность связана с недостаточным количеством уравнений для однозначного вычисления указанных реакций. Задачу снятия этой неопределенности решают по-разному. В монографии [7], например, рассматривается задача оптимального распределения реакций по точкам опоры, которая сводится к задачам линейного и квадратичного программирования. Часто используют датчики, измеряющие опорные реакции в местах контакта ног с ОП [10–12]. В настоящей статье указанная неопределенность снимается либо путем использования пассивных кинематических пар (КП), либо использованием модели Кулона с условием отсутствия проскальзывания опорной ноги относительно ОП. В последнем примере настоящей статьи демонстрируются оба подхода.

Моделирование ШМ иногда начинают с моделирования колесно-шагающей машины (КШМ), у которой конструкция одной или двух ног повторяет конструкцию ног ШМ. Это позволяет на простых моделях решить ряд задач, возникающих в расчетах ШМ.

Постановка задачи : рассмотреть класс ШМ и КШМ, у которых движителем является одна или несколько ног, подвешенных к корпусу, где последняя кинематическая пара каждой ноги является поступательной; разработать формализм вывода формул вычисления динамических реакций в опорных точках ног, а также движущих сил и моментов сил в кинематических парах ног для заданных абсолютных ускорений центров масс и скоростей кинетических моментов относительно центоров масс каждого тела рассматриваемых машины; привести примеры, в которых записать условия реализации шага без проскальзывания опорных ног относительно ОП.

1.    Основные расчетные формулы

Тело с порядковым номером i и его массу обозначим через moi. Для сокращения записей будем использовать следующие аббревиатуры: ПТ(i) - полюс тела moi; ЦМ(i) - центр масс тела mot; БТ(0 - база тела mot; Kn(i) - кинематическая пара, связывающая тело mot с БТ(i); nKn(i) -поступательная Kn(i); BKn(i) - вращательная Kn(i). Будем использовать следующие обозначения: Oj - ПТ(у); Cj - ЦМ(у); WCj - абсолютное ускорение ЦМ(/); Pj = mojg - вес тела moj; aj = \OjCj\ - расстояние от ПТ(у) до ЦМ(/); cj- - орт, указывающий направление из ПТ(у) в ЦМ(/); у - орт вертикали; д - ускорение свободного падения; KCj - кинетический момент тела mOj относительно ЦМ(j); Sj - множество номеров тел, образующих КП с телом mOj; Rk = OjOk -межполюсный вектор КП(к) для к. 6 Sj, т. е. j = к — 1; Fj, Mj - главный вектор и момент относительно ПТ(j) сил реакций, действующих на тело mOj со стороны мысленно разорванных связей при переходе от древовидной системы тел с циклами (с замкнутыми ветвями) к системе тел с открытыми ветвями, а также изоляции системы тел от действия внешней среды.

Согласно утверждению 7 книги [13] сила F i и момент силы M i относительно ПТ(0, действующие на тело m_O i со стороны БТ(i), можно вычислять по следующим векторным обратным рекуррентным формулам (ОРФ):

Fj = mojWC]- + Цу — F- + Xkcsj Fk,(1)

Mj = ajCj X (mojWcj + Pj'y) + Fcj — Mj + XkeSj (Rk x Fk + Mk),                       (2)

где j = N,N — 1,...,i; N - номер последнего тела системы тел.

Если концевое тело mOk является колесом и ЦМ(к) лежит на оси его вращения, то, совместив ПТ(к) с ЦМ(к), получим ak = 0 и уравнение (2) примет вид —  —— г

Mk = Kck — Mk.(3)

Для системы тел на плоскости

• pc = I^jq,                                   _(4)

где I j - момент инерции тела m_O j относительно оси C j q; a j - абсолютное угловое ускорение тела m_O j ; q - орт нормали к плоскости движения тел.

Из F k и M k можно выделить динамические реакции (реактивные составляющие), движущие силы и моменты сил. Реактивные составляющие удерживают тело m_O k от относительных движений, недопускаемых связями. Движущие составляющие обеспечивают относительные движения тела m_O k в направлениях, допускаемых связями.

В ПКП(к) тело m_O k может двигаться поступательно относительно БТ(к) вдоль оси O kPk , жестко связанной с телом m_O k , где р_к - орт оси ПКП(к), указывающий положительное направление поступательного движения. В ПКП(к) сила реакции F_r k , перпендикулярная оси O k P k , и момент силы M k относительно ПТ(к) являются реактивными. Вектор M k неизвестен по модулю и направлению. Для F_r k неизвестны модуль и направление в плоскости, перпендикулярной оси O k P k • Следовательно,

F_k =Jrk + F k P k ,     _                                                           (5)

где р_к ■ F_r k = 0, F k =P k ' F k - сумма движущей силы и силы трения в ПКП(к). Если в ПКП движущая сила отсутствует, то F k - сила трения в ПКП(к).

В ВКП(к) тело m_O k может вращаться относительно БТ(к) вокруг оси O k q k , где q_k - орт оси ВКП(к) и положительным считается вращение против хода стрелки часов. К реактивным в ВКП(к) относится сила реакции F k , неизвестная по модулю и направлению, и момент M_r k относительно ПТ(к) силы реакции. Момент M_r k перпендикулярен оси O^k . Следовательно,

M_k M rk + M_kq_k,    _                                                      (6)

где q_k ■ M_r k = 0, M k = q_k ■ M k - сумма движущего момента силы и момента силы трения в ВКП(к) относительно оси O k^k . Если в ВКП(к) движущий момент силы отсутствует, то M k -момент силы трения в ВКП(к) относительно оси O^ k .

испо л ь зуют дл я иссл едо вания хо дьбы по горизонтальной или наклонной прям о й. Н а р ис. 1 изо бра ж е н а п ро с те й ша я К ШМ в в е рти к а л ьн ой п лоск о с ти с од н ой од н озв е нной ногой, образующей с корпу с ом ПК П, в к оторой гори зо нтальный корпус является направляющей. Н а ри с . 2 изображена К Ш М с п олярн ой н ог ой, в к оторой корпус и нога меняют свою ориентацию в п роц е сс е в ып о лн е н и я ша га . Д ля с озда н и я ма к е тов так и х К ШМ н е о б ход и ма о д на ПКП и колесная пара. КШМ на рис. 1, 2 с о с тоят и з тре х т е л, и х д вижителем является ПКП с приводом (актив н а я ПК П) . К Ш М н а рис. 3, 4 с ос тоят и з ч е ты ре х те л . Д в ижи те ль ( н о г а ) К ШМ на ри с . 3 состоит из двух активных ПКП. Нога КШМ на рис. 4 с од ержи т ак ти в ну ю В К П, за которой следует активная ПКП.

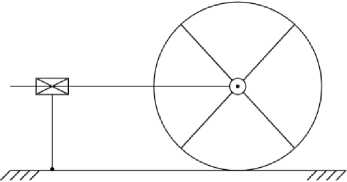
Рис. 1. Простейшая колесно-шагающая машина Fig. 1. The simplest wheeled walking machine

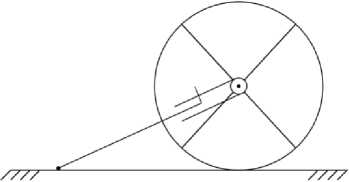
Рис. 2. Колесно-шагающая машина с полярной ногой Fig. 2. A wheel-walking machine with a polar foot

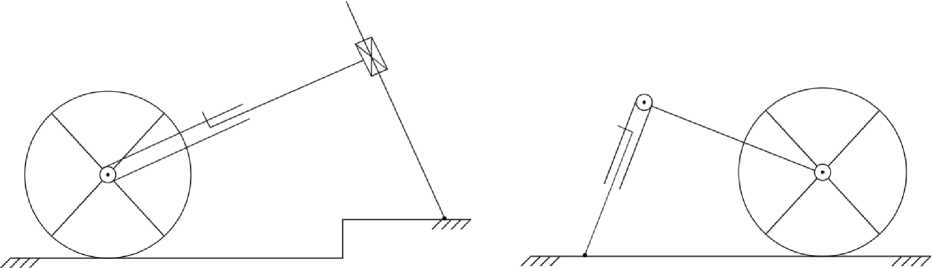
Рис. 4. Колесно-шагающая машина с полярной ногой и корпусом Fig. 4. Wheel-walking machine with polar foot and hull

Рис. 3. Колесно-шагающая машина с декартовой ногой

Fig. 3. Wheel-walking machine with a Cartesian foot

К Ш М в горизон та л ьн ой п лос к о с ти с дв умя тре хзв е н н ыми д екартовыми, цилиндрическими и л и а н гу лярн ыми н ога ми мод е ли руют для исследования ходьбы по горизонта ль ной и н ак лон н ой п л ос к о с ти . К ШМ с д в у мя тре хзвенными сферическими или ангулярными н ога ми мод ели ру ю т для и с сле д ов а н и я ход ь б ы п о с л ожн ой ОП в п рос тр а н с тв е . С мот рите, например, двухногую КШМ в монографии [8, с. 239].

В п роц е сс е мо д е ли рова н и я, расчета, конструирования и создания протот и п а Ш М рек оме нду етс я с озд а ть и и с с л е д ов а т ь ма к е т КШМ, у которой конструкция ноги совпада е т с к он с тру к ц и ями ног ШМ [8]. Например, пер ед м од е лиров а н и е м ШМ н а рис . 5 рекомендуется рассмотреть КШМ на рис. 4.

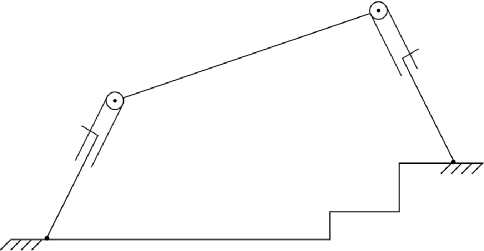
Рис. 5. Схема макета шагающей машины для исследования одного шага

Fig. 5. Schematic diagram of a mock-up of a walking machine for a single step study

Без наличия трения в точке контакта стопы КШМ с ОП организовать движение его корпуса относительно ОП невозможно. Поэтому коротко обсудим виды трения, действующие на тела КШМ.

Трение является причиной сопротивления движению соприкасающихся тел относительно друг друга. В зависимоти от относительного движения трущихся тел различают трение скольжения, трение качения и трение верчения. На практике перечисленные виды трения могут иметь место одновременно, например, колеса автомобиля могут одновременно катиться, скользить и вертеться на поворотах. В КШМ при взаимодействии колеса с ОП могут иметь место одновременно все три вида трения, а при взаимодействии ноги с ОП может одновременно иметь место трение скольжения и верчения.

При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения тел возникает сила трения скольжения, которую иногда называют трением первого рода [14]. Эта сила трения препятствует скольжению взаимодействующих тел относительно друг друга. Если колесо катить или стремиться катить по ОП, то кроме силы трения скольжения из-за деформации поверхностей взаимодействующих тел дополнительно возникает пара сил, препятствующая качению колеса, которую иногда называют трением второго рода [14].

ОП является связью для концевых тел (колес и стоп ног) КШМ. Если поверхности соприкасающихся тел абсолютно гладкие, то реакция ОП направлена по нормали к общей касательной в точке контакта и ее направление не зависит от действия на ногу активных сил приводов ее тел. От этих сил зависит только модуль (числовая величина) силы реакции. В действительности абсолютно гладких ОП как и абсолютно твердых тел не бывает. Все тела деформируемы и их поверхности в той или иной степени шероховаты. Поэтому реакция ОП зависит от активных сил приводов ноги как по величине, так и по направлению, т. е. ее можно разложить на составляющие, одна из которых направлена по общей нормали к поверхности соприкосновения, а другая (сила трения скольжения) лежит на этой поверхности.

Если конец последнего тела т_ок ноги соприкасается с ОП, то сила F k реакции шероховатой ОП, действующая на тело т_ок , зависит от активных сил в КП ноги как по величине, так и по направлению. Если F_k разложить на составляющие, одна из которых F_yk направлена по общей нормали к поверхности соприкосновения, а другая F_tk находится в касательной плоскости к этим поверхностям, то составляющая F_tk является силой трения скольжения, а составляющая F y _k - нормальной реакцией. По модели Кулона модули этих составляющих связаны друг с другом. Если сила реакции F k уравновешивает активные силы (движущие силы приводов ноги), то F_t k < f₀F_yk , F_t k = fF_y k где f₀ - коэффициент трения покоя, f - коэффициент трения скольжения (f < f₀ ). В первой задаче динамики машины абсолютное движение корпуса и ног задается. Поэтому часто удается определить направление реакции F_t k . Например, если в плоской модели КШМ или ШМ корпус движется вдоль оси Ох, то F_t k = -F_X k и

F k = -F_XkX + F yky , F_X k < f o F yk , (7) где F_X k - модуль силы трения, связанной с силой нормального давления формулой Кулона F_X k = fF yk . Неравенство в формулах (7) является условием отсутствия проскальзывания ноги ШМ относительно ОП, т. е. это условие реализации шага.

Части тел ВКП, находящиеся в соприкосновении, называют шипом и подшипником. Подшипник воспринимает как радиальную (перпендикулярную оси ВКП), так и аксиальную (колли-ниарную оси ВКП) нагрузку со стороны шипа. Моменты сил трения, вызванные каждой нагрузкой, определяются отдельно. От радиальной нагрузки модуль момента силы трения в ВКП(^) вычисляется по формуле [15]

M k = rfN_r k , (8) где г - радиус шипа и подшипника; f - приведенный коэффициент трения, N_r k - радиальная нагрузка в ВКП(^). Величина f безразмерная и зависит от конструкции ВКП [15].

При качении колеса m0k по горизонтальной ОП в результате их деформаций соприкосновение m0k с ОП происходит по небольшой дуге, смещенной в сторону движения вместе с точкой приложения вектора Fk. Величину ft этого смещения называют коэффициентом трения качения. Поэтому модуль силы трения качения, приведенной к оси вращения колеса, вычисляется по формуле [15]

M^r_k = \f t F_yk-RF_xk\,                                                           г        (9)

где R - радиус колеса; F_xk,F_yk - касательная и нормальная составляющая реакции F_k; f_t - коэффициент трения качения.

• 3.    Общий формализм решения первой задачи динамики машин

Для решения первой задачи динамики колесных, колесно-шагающих и шагающих машин рекомендуем последовательно выполнить действия следующих девяти этапов. Подробности этого формализма рассмотрим в процессе решения конкретных задач в порядке от простого к сложному.

Этап 1 . Корпус и тела всех движителей (ног и колес с их подвеской) последовательно занумеровать числами 1, 2, 3, 4, ..., N, где N - общее количество подвижных тел машины. Тогда т₀₁ -корпус, т₀₂ - первое тело первого движителя (для ШМ первой ноги), т₀₃ - второе тело первого движителя, т₀₄ - третье тело первого движителя, т₀₃ - первое тело второго (трехзвенного) движителя и так далее. Изобразить кинематическую схему машины в исходном относительном положении тел ВКП, указать ПТ(i) и ЦМ(i), мысленно закрепить за телами связанные системы координат CCK(i) O j X iy^ Z i , где х^ - орт горизонтали, y_t - орт вертикали, z_t - орт, дополняющий орты Х( , у до правого репера. При необходимости описать параметры q j относительного положения тел машины. Перечислить нулевые и постоянные значения величин, входящих в формулы (1), (2). Выразить орты p, , q_t , С( и межполюсные векторы R i через орты ССК тел или орты х, у, Z правой неподвижной системы координат, где ось Ох горизонтальна, ось Оу вертикальна, т. е. д = -ду.

Этап 2 . Мысленно устранить связи движителей (колес, ног) с ОП, заменив их реакциями F i , Mi , где i Е N₀ - множество номеров последних тел опорных движителей машины (опроных ног). Если на корпус (тело т₀₁) действуют внешние силы и/или моменты сил, например, порывы ветра, то необходимо их заменить соответствующими реакциями F₁ и/или М₄ .

Этап 3 . Для концевого тела т₀ 1 по ОРФ (1) выписать формулу

F^moiWi + Piy-SSi,(10)

где i Е N_e - множество номеров концевых тел машины; S i = 1 если i Е N₀ , иначе S i = 0.

Если m₀ i _-1 - предпоследнее тело движителя, то по ОРФ (1) с учетом (10) выписать формулу

Fi-1 = moi-1Wci-1 + Pi-1y + Fi = 2j=i-1 mojWcj + Р1-1У - ^i, где P- = Pi-1 + Pi = (m0i-1 + m0i)д - вес двух последних тел движителя.

Аналогично, если m₀ i _-2 - первое тело движителя, то по ОРФ (1) с учетом (11) выписать формулу

Fi-2 = moi-2Wci-2 + Pi-2y + Fi-1 = 2j=i-2 mojWcj + Pdy - SiFi, где Pd = Ej=i-2 Pj = д Zj=i-2 m0j - вес движителя (ноги).

Этап 4 . Для каждой ПКП(0, используя выписанные на этапе 3 силы, записать формулу вычисления искомой движущей силы F i = p i ■ F i .

Этап 5 . По ОРФ (1), используя формулы (12), выписать векторное уравнение

F = т 01 ^_С 1 + P1y - S 1F[ + 2 k. s ^Fk = 2 7=1 m o■ W_C j + Py - E ien₀ ^ - ЪК = 0,   (13)

где S₁ - множество номеров тел, смежных корпусу т₀₁; P = 2 7=1 P j = д2 7= ₁ m₀ j - вес машины. S₁ = 1, если F₄ - сила реакции внешней среды, введенная в обращение в процессе изоляции машины от действия внешней среды. Иначе S₁ = 0. Из векторного уравнения (13) получить два (для модели машины на плоскости) или три скалярных уравнения, т. е. проекции уравнения (13) на оси Ох, Оу, Oz. Подробности рассмотрим в конкретных примерах.

Этап 6 . По аналогии с этапом 3 для каждого движителя по ОРФ (2) выписать формулы вычисления векторов M i , где i пробегает номера тел движителя от последнего до первого.

Для концевого тела m_o - по ОРФ (2) выписать формулу

^M i = ^a t ^C t ^X (^m oi ^ ci + ^P i ^y'⁾ + ^ ci - ⁸ i ^M i .                                                 ⁽1⁴⁾

Если m_o - _-1 - тело движителя, то по ОРФ (2) выписать формулу

^M i-1 = ^a i-1^Fi-1 ^X (^m ot-i ^ ci-i + ^ i-i ^y) + ^R ci-1 + ^R i ^{X F} i + ^M t , где с учетом формул (10), (14) имеем

^R i ^{X F} i + ^M i = ^R i ^{X (m} oi ^W ci + P i ^{y — 8} i ^F i ) + a i C i X (^m ot ^ ct + Р^у + ^ ci ^{— 8} i ^M i • Следовательно,

^M i-1 = ^E j^i-1 ^[a j ^C j ^{X (m} oj ^W cj + ^P j ^y + R cj ] + ^R i ^{X (m} oi ^W ci + P i ^{y - S} i ^F i ) ^{- S} i ^M i •    ⁽¹⁵⁾

Аналогично, если m_o - _-2 - тело движителя, то по ОРФ (2) выписать формулу

^M i-2 = ^a i-2 C i-2 ^{X (m} oi-2 ^W ci-2 + ^P i-2 ^y + ^R ci-2 + ^R i-1 ^{X F} i-1 + ^M i-1 , где с учетом формул (11), (15) имеем

^R-1 X F^ + Mi -1 = R i-1 X (m oi-1 W ci-1 + m oi W ci + P — y - 8^-) +

+ S }=i-1 [^a j C j ^{X (m} oj ^W cj + ^P j ^y) + ^р_п\ + ^R i ^{X (m} oi ^W ci + ^P i ^y - ⁸ i ^F i ) - ⁸ i ^M i • Следовательно,

^M i-2 = 'E^l j=i-2 ^[a j ^C j ^{X (m} oj ^W cj + ^P j ^y) + ^R cj] + ^m oi-1 ^R i-1 ^{X W} ci-1 +

^+m oi ^(R i-1 + ^R i ) ^{X W} ci + ^(P i- ₁ ^R i-1 + ^P i ^R i ^{) Xy — 8} i ^(R i-1 + ^R i ) ^{X F} i ^{— 8} i ^M i •            ⁽¹⁶⁾

Этап 7 . Для каждой активной ВКП(г), используя выписанные на этапе 6 моменты сил, вывести формулы вычисления искомых движущих моментов сил M - = q - ■ M - .

Этап 8 . По ОРФ (2), используя формулы (16), выписать уравнение

M_t = a 1C1 X (m o1 Wd + P i y) + K_ci -m[ + E kes , (^R k XF_k+M_k) = 0.         _  _ (17)

Из векторного уравнения (17) получить его проекции на одну, две или три оси Ox, Oy, Oz в зависимости от подпространства, в котором движется ШМ (вертикальная плоскость, горизонтальная плоскость или пространство Oxyz)

Этап 9 . Из уравнений, полученных на пятом и восьмом этапах, выразить динамические реакции и подставить их в искомые формулы вычисления движущих сил и/или моментов сил, полученных на четвертом и седьмом этапах. Записать условия реализации шага. Подробности продемонстрируем на конкретных примерах.

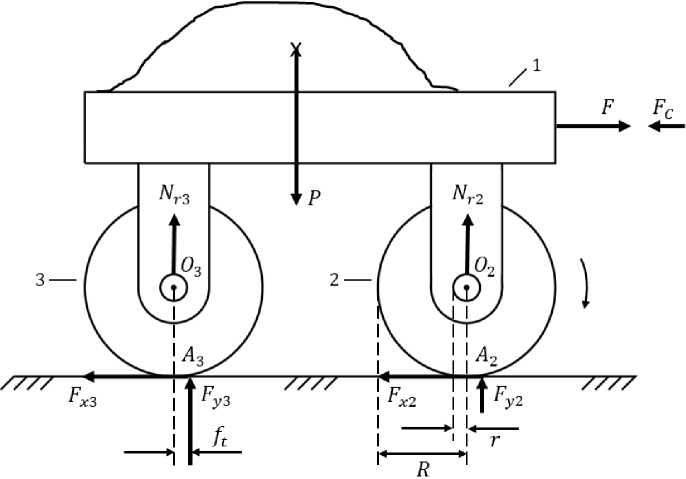
Рис. 6. Колесная машина Fig. 6. Wheeled car

—г

F₁ - си ла р е а к ц и и в н е ш н е й среды, введенная в обращение в процессе из ол яц и и маш и н ы от де й с тв и я вн еш н е й с ре ды. При ц е п н е н а ход и тс я п од прикрытием тягача, т. е. сила сопротивления воздуха F_c н аправл е н а п ро тив т ягов ого у с и л ия F, которое необходимо определить. Таким образом, F_r = (F — F_c)x, М_г = 0.

Этап 3 . П о форму ле ( 1 0) для i = 2,3, учитывая, что S i = 1, выпишем

Этап 4 . П К П в ма ш и н е отс у тс тв у ю т.

Этап 5 . П о форму ле ( 1 3) для i = 1, учитывая, что S₁ = {2,3}, 5₁ = 1, получим

Fi = E j-i (m oj W cj — F^ + Py = 0,                                             (20)

где P = Е^ Pj = pEj-1 moj - вес машины. Проекция уравнения (20) на ось Ох с учетом (18) имеет вид x-F1 = x- {Ej-i mojWcj + Fx2x + Fx3x — Fx + Fx) =

= ^x • ^{E j}-i ^m oj ^W cj + ^F x2 + ^F xj ^{— F + F} c = 0.

Отс юд а ис к омо е тягов ое уси ли е

F = x^E^3j -i m oj W cj + F_x2 + F_X j +F c .                 _                        (21)

Проекция уравнения (20) на ось Оу с учетом равенств (18), у • Wcj = 0 имеет вид y^Fi = P — Xl-2 Fyj = P — Fy2 — Fyj = 0,

• т. е. F_y2 + F_yj = P - си ла н ормальн ого д а в ле н и я п ри ц е п а на ОП.

Этап 6 . П о форму ле ( 1 4) с у че том форму л ( 4) , a j = —q j , (19) для колес m_o j (j = 2,3) получим

M j = —I^q- — М^Г = —I_J^cq j q_j + (RF xj — f_tF yj)q _j .                                  (22)

Этап 7. Колеса прицепа являются ведомыми, т. е. ВКП пассивные. Тогда по формуле (6) Mj = q. • Mj - момент силы трения, действующей в ВКП(у) со стороны mol на moj и вычисляемый по формуле (8), т. е. Mj = rfNrjqj, где г - радиус шипа и подшипника в модели ВКП; f - приведенный коэффициент трения в ВКП(у), Nrj - сила давления кузова с грузом на ось колесной пары moj. Отсюда с учетом (22) получим rfNrj = —Ijqj + RFxj — ftFyj,

• т. е. F_X j R = Ijq j + rfN_r j + f_tF_y j , j = 2,3. После суммирования по j и деления на R получим

• 5.    Простейшая КШМ

P_X 2 + F_X 3 = Ц-Ъ/К + rf(N_r2 + N_r3)/R + f_t(F_y2 + F_y3)/R,

F_x2 + F_X 3 = lift/R + rfPJR + f t P/R,                                          (23)

так как N r2 + N r3 = P i = m₀₁g, F y2 + F y3 = P.

Этап 8 . В в ы п и с ыв а н и и уравнения (17) и выполнении последнего этап а н е т н е об ход и мо с ти , так к ак , п одс та в и в (23) в ( 21), пол у чим и с к ому ю д ви жу щ у ю си лу , гд е

W cj = fax , q j = fa/R, x ■      m oj W cj = fa E³₌ i m oj .

На рис. 7 и з ображе н а КШМ, корпус которой образует с ногой активную ПК П и п а с с и в н у ю В К П с к ол е с ной п а рой . Э та К ШМ предназначена для исследования услов и й ре али за ц ии од ног о ша га, а так ж е для э к с п е р и ме н та льн ог о оп ред е ле ни я к оэ ффи ц ие н тов трения скольжения и качен и я. Зде с ь д ля реш е н и я пе рв ой задачи динамики с выводом условий реализ ац и и од н ого ша га б уде м с чи та ть, что к ол е с о к атится п о ОП б е з ск ол ьж ени я.

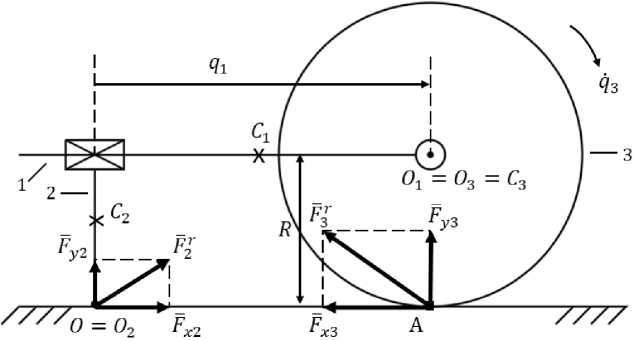
Рис. 7. Простейшая колесно-шагающая машина для исследования одного шага

Fig. 7. The simplest wheel-walking machine for the study of a single step

Этап 1 . К ШМ с ос тои т и з тре х те л , т. е. N = 3, где m_oi - корпус в виде горизонтального цилиндра, m_o2 - но га в в и д е в ертик аль ного сте рж н я , m_o3 - колесная пара (далее колесо). Нога и кол есо вза и мод ейс тву ют с О П.

Пара ме тры относител ьн ого п оло же н и я те л : q_i = q₂ = ОА; q₃ - угол поворота колеса относительно корпуса.

а з = 0, р₂ = -х, q₃ = z, fa = -x, C 2 = у, fa = 0, R 2 = О_ГО₂ = -q i X - Ry,

Р з =ОЮ₃ = 0, S i = {1,2}, S i = 0, W c2 = ^ c2 = 0, F a = 0.

Этап 2. Мысленно разорванные связи ноги и колеса с ОП в точках О2 и А заменим реакциями —r —r                                         r_ _

Fj, Mj, где j = 2,3. Из рис. 7 видно, что разложения Fj на составляющие вдоль осей Ох, Оу имеют вид fa = FX2X + Fy2y, fa = -FX3X + Fy3y.(24)

r

С л е д ов а те л ьн о, моме н т ы си л F j относительно точек О j , действующие со стороны ОП на тело m_o j , вы числяю тс я п о формул а м

Mr = 0, M33 = -RFx3z.                               _(25)

Этап 3 . Д л я н оги и к олеса п о форму ле (10) с у че том ра в е н с тв W_c2 = 0, S₂ = 1 выпишем

—      - _   — r        r —      - ——r

F 2 = m o2 W c2 + Р 2 У - 5 2 F 2 = Р 2 У - F 2 , F 3 = m o3 W c3 + Р 3 У - S 3 F 3 .

Этап 4. ПКП(2) активная, т. е. со стороны корпуса (тела moi) на ногу (на тело mo2) действует движущая сила _  —    _   _  — r — —r __

F2=P2^ F2 = -X ■ (Р2У - F2) = X ■ F2 = х ■ (Fx2X + Fy2y = Fx2.(26)

Этап 5 . П о форму ле ( 1 3) в ы п ише м век торн ое у ра в не н и е

Fi = SU mOjWcj + Py- S3 : 8tF- = 0,(27)

где P - вес К ШМ. М а ш и на ра б отает в вертикальной плоскости. Поэтому из в е к торн ог о у ра в н ения (27) с учетом равенств у • W_c j = 0, х • Y /- _i m_O j W_C j = m_i3q_i, где ^т ₁ з = ^т о ₁ + ^т оз получим два скалярных уравнения (проекци и н а ос и Ох, Оу)

xfa = m-33qr-Fx2+Fx3 = Q, yfa = P-Fy2-Fy3 = 0.(28)

Этап 6 . Д л я н оги и к олеса п о форму ле (14) в ы пишем

М₂ = а 2С2 X (m o2 W c2 + Р 2 У ) + «С 2 - 8 2 М2 = a₂y * Р 2 У = 0, № 3 = К_с3 - М3.

Этап 7 . Кол е с о п ас сив н ое ( в е дом о е ), т. е. М₃ = 0. Следовательно, с учетом формул (6), (25)

Мз = д3^Мз=^Ксз + RFX3Z • z = 1^аз + RFX3 = 0.(29)

Этап 8 . П о форму ле ( 1 7) с у че том ра в е н с тв

W ci = i i x, K ci = 0, R 2 = - q i x - Ry, R 3 = 0, № 2 = 0, C i = -x выпишем векторное уравнение

M i = -a i P i X Xy + S_k =2 (R_k xF_k + M_k) = -a i P i Z + М 3 - fax + Ry) X fay - F₂) = 0. Проек ци я э того у ра в н е н ия н а ос ь Oz с учетом равенств (24), (29) принимает вид

^-a i ^P i ^{- q} i ^P 2 ^{+ lCa} 3 ^{+ q} i ^F y 2 ^{- R(F} X2 ^{- F} X3 ) = 0.                                     ⁽³⁰⁾

Этап 9 . И з у ра в н е н и й ( 28 ), ( 29), ( 30 ) п олу чи м

^F X2 ^{- F} X3 = ^m 13 ^q 1 ^ ^F y2 ^{+ F} y3 = ^P,F X3 = ^-I3^a 3 ^/R,

^-a i ^P i ^{- q} i ^P 2 ⁺ 1 з ^а 3 ^{+ q} i ^F y 2 = ^R(F X2 ^{- F} X3 ) = ^Rm i3 ^q i .

Отсюда

^F X2 = m i3 q i + F x3 = m i3 q i - I^/R,

F y2 = (Rm i3 q i + a i P i + q i P 2 - I^/q i ,^ =P- ^F y2 .

Те пе рь п о формул е (26) полу чи м иск омую форм у л у в ычи с л е н и я д в и жуще й с илы ноги

^F 2 = ^F X2 = ^m i3 ^q i ^{- I} 3 ^a 3 ^/R .                                                            ⁽³¹⁾

Условие реализации шага имеет вид Fx2 < foFy2. Отсюда m^qi - I^/R < fo(Rmi3qi + aiPi + qiP2 - 1^3)^, где qi = -Rq3, аз = -q3.

6.    КШМ с полярной ногой

На рис. 8 и з ображе н а КШ М, корпус которой образует с ногой активную ПК П и п а с с и в н у ю В К П с к олес н ой п а рой . В отли чи е от К Ш М н а ри с. 7 здесь корпус и нога меняют свою ориентацию в вертикальной плоскости.

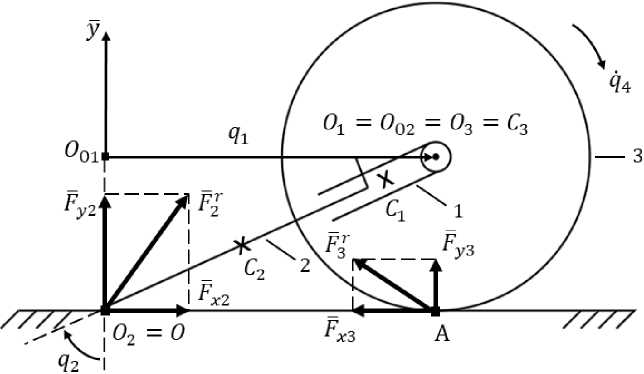
Рис. 8. Колесно-шагающая машина для моделирования одного шага Fig. 8. A wheel-walking machine for single-step modeling

Этап 1 . КШМ состоит из трех тел, т. е. N = 3, где m_0i - корпус в виде направляющей для ноги, т_о2 - нога в виде стержня, т₀₃ - колесная пара (далее колесо).

Параметры относительного положения тел: q_i = О₀₁О₁ - положение полюса О₁ корпуса на оси Ох; q₂ - угол поворота корпуса вокруг оси O_rz; q₃ = О_о2О₂ - положение опорной точки ноги относительно полюса корпуса; q₄ - угол поворота колеса относительно корпуса. В исходном положении q_i = q₂ = q 4 = 0, q₃ = О ^ А = R.

а з = 0, P₂ = -У₂, Я₂ = Я₃ = z, Ci = -У₂, C 2 = У₂, c₃ = 0,

R 2 = ОО₂ = -q i X-Ry, R₃ = ОО₃ = 0.

Этап 2 . Мысленно разорванные связи ноги и колеса с ОП в точках О₂ и А заменим реакциями F } , м ] , где j = 2,3,

К = F_X 2 X + Р_У 2 У, М [ = 0, F₃ =-F_x3X + F_y3y, M^r₃ = -RF_x3z.                    (32)

Этап 3 . Для ноги по формуле (10) выпишем

F₂=m o₂ W_c2+P₂y-F ^r ₂ .      _      _                                   (33)

Для колеса по формуле (10) выпишем F₃ = m_o3W_c3 + P₃y - F₃.

Этап 4 . ПКП(2) активная. Формула вычисления движущей силы имеет вид

^F 2 =P₂-F 2 = ^-У₂ ■ ^(m 02 ^W c2 + ^P 2 ^{y -} К) = ^-m 02 ^y ₂ • ^W c2 ^{- Р}2^У₂ 'У + У^ ^(F x2 ^X + ^У), т. е.

F 2 = W^P + X y2 F x2 + У у2 К у2 ,                                                         (34)

где W 2 ^P = -т о2 У₂ • W c ₂ - Р 2 У у2 , X y2 = У₂'Х, У у2 =У₂'У. ^r

Этап 5 . По формуле (13) выпишем F_r = X j _-i m₀ j W_c j + Ру - Y 3 _-2 F t = 0, где Р - вес машины. Из этого векторного уравнения получим два скалярных уравнения в проекциях на оси Ох, Оу

X'£3j=im0jWcj-Fx2+Fx3 = 0, y'X3^im0jWcj + P-Fy2-Fy3 = 0.(35)

Этап 6 . Для концевых тел по формуле (14) выпишем

М2 = а2с2х(то2Шс2+Р2у)+Кс2, М3=Кс3-МГ3.(36)

Этап 7 . ВКП пассивная. Тогда по аналогии с этапом 7 предшествующей задачи получим

Fx3 = -Ka JR._

Этап 8 . По формуле (17) с учетом (33), (36) и равенства R₃ = 0 выпишем

Mi = aiCi х (m0iWci + Piy~) + Kci + R2 x F2 + М2 + М3 = Wc — R2 x F2 — М3 = 0,(37)

где W_c = Y j-i [a jCj x (m_0]■W_C]■ + P j y) + K_c j + K_c3 + R₂x (m₀₂W_c2 + P₂y) Проекция уравнения

• (37)    на ось О ^ Х с учетом равенств (32) принимает вид

Z'WC-R2x (Fx2x + Fy2y) •X + RFx3=X'Wc + R2' (^У - FyJ) + RFx3 = 0,(38)

где R₂ • (F x2 y - F y2 X) = - fax + Ry) • (F x2 y - F y2 X) = q i F y2 - RF x2 .

Этап 9 . Из уравнений (35), (38) и выражения F_x3 = -I₃a₃/R получим

F x2 - F x3 = F x2 - I^/R = W x , F y2 + F y3 = W^p,

RFx3 + qiFy2 - RFx = -13^3 + qiFy2 - RF^ = Wz,_ где Wx = X • Ey-i mо]■Wc]■, WyP = y • Ey-i m0jWcj + P, Wz =-z • Wc. Отсюда

F x2 = W x + I^/R, F y2 = (W z + №3 + RF^fa = [W z + №3 + R(W x + I^/W/q i .

Следовательно, согласно (34) искомая движущая сила вычисляется по формуле

F 2 = W 2 ^p + X y2 ^F x2 + y y2 ^p y2 = W^p + X y2 (W x + P^/R^ + y y2 (W z + RW x + 2i c a 3 )/q i .

Условие реализации шага имеет вид F_x2< f₀F_y2, т. е.

W x + I^/R < f,(W z + RW x + 2i c a 3 )/q i .

7.    Решение первой задачи динамики ШМ с управляемой длиной ноги

Рассмотрим двухногую ШМ в двухопорном состоянии (рис. 9), в которой первое тело ноги образует ВКП с корпусом, второе тело с первым образует ПКП. Рассматриваемая модель ШМ предназначена для исследования условий реализации одного шага без учета динамики переносных ног.

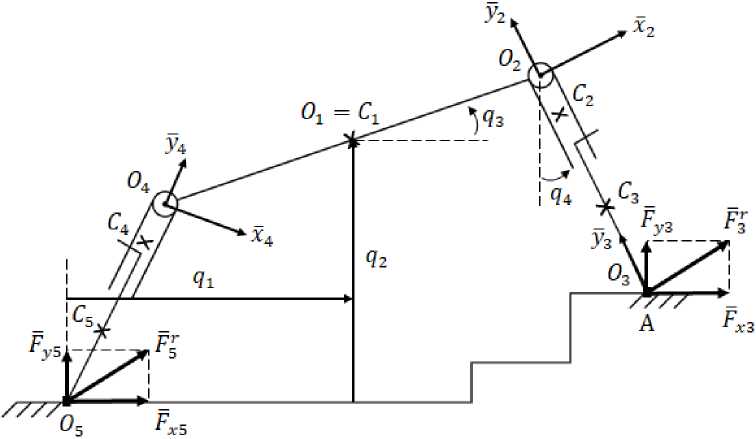
Рис. 9. Шагающая машина для моделирования одного шага и условий его реализации Fig. 9. A walking machine for modeling a single step and its implementation conditions

Этап 1 . ШМ с ос тои т и з сле д у ю щ и х те л : m_o1 - корпус; m_o2, m_o3 - тела передней опорной ноги; т_о4, т_о5 - т ела зад н е й опорной н оги . В ис ход н ом п ол оже н и и тел о с и О - х - у -г- их ССК параллельны ортам %, у, z.

Через О - о б означе н п ол ю с в торого те ла m_o - рассматриваемой ноги, т. е. i Е {3,5}. О -^ - по л ю с пе рв ого те л а рас с ма т ри в а е мой н оги . R - = О -_ ₁О - = -Ь_ц - у - , Ь_ц - - длина ноги с опорной точкой O i . Д а ле е и с п ользу ю тс я с ле д у ю щ ие п а ра м е тры :

N = 5, О 1 = С 1 , Й 1 = 0, 8₃=8₃ = 1, р. = -у . , q^ = Z i_i , Ci = у, , Ct-1 = -у , С 1 = 0.

Этап 2 . Мы сле н н о у с тра ни м связь опорных ног с ОП, заменив их реакция ми

F^r i = F_xix + F_yiy, M^r_t=0.                                                             (39)

Здесь и далее i Е N_o = {3,5} - множество номеров концевых тел опроных ног, P_X - , P y- - проекции

—r_ _ вектора P- на оси Ox, Оу соответственно.

Этап 3 . Для i Е N_o по форму ле ( 10) вы п ишем

Т1 = т01^с1 + !.1у-ТГ.(40)

Для первых тел ног по формуле (11) выпишем —    — р

Fi_i = Wi_i-Fi, _(41)

где W ._i = X }^i- ₁ m oj W cj + P_ny, P_n = P-^ - вес ноги.

Этап 4 . Ис п оль з у я форму лы (39), (40) для вычисления искомой движуще й с и л ы ПК П н оги, получим

Fi = Pi-Fi = -yr (motWct + P-y) -F-= W* + FXiXyi + Ру-уу-,(42)

где х_у - = x - у - , у_у - = у - у - - направл я ю щ и е к о с и н у с ы н оги в СС К ОП Оху,

W У■ = -y_i■(m oi W_ci + P_iy) .

Этап 5 . Д л я к орп уса п о ф орму ле ( 13) вып и ш е м Р₁ = ^ 7= ₁ m_o j W_c j + Py - Тлеи₀ P i = 0, где P - в ес ШМ. В з яв п роек ц и и э того у ра в н е н и я н а ос и Ох, Оу, получим

F x₃ +F x₅ = W x , P y ₃+P y ₅ = W y^P ,          _                                  (43)

где W x = x- X^N₌ 1 m oj W cj , W y^P = P + у - ^=1 m oj W cj .

Этап 6 . Д л я п е рв ого те л а н оги п о фо рму ле ( 15 ) с у че том ра в е н с тв а R - = -Ь_ц - у - выпишем

M . 1 \У . 1 + L ^. v . / Р^Г ,                                                                                  (44)

где W -“_1 = X j=--1 [a jCj x (m oj W cj + P^) + K cj] - Ь ц- у . x (m o- W c- + P - у).

Этап 7 . Из (44) с учетом равенств q_i _ ₁ = z — = z - , z — xy i = —x - получим

M i-1 = q^ • M^ = z_j _ ₁ • (W _ + L qi y xF-) = z^ • W^_ -1 — L_qix_l • F - .

a

Отсюда с учетом (39) и обозначения ^ -_ ₁ = z -_ ₁ • W i _—1 формулы вычисления движущих моментов сил ВКП ноги принимают вид

M i-1 = W -1 — L qiXi ^^Г1 = W^ — L qi (F_X i X_X i + F_y i y_X i ),                              (45)

где X xi = x • х - , y xi = y х - .

Этап 8 . По формуле (17) с учетом равенств а₁ = 0, M₁ = 0 выпишем векторное уравнение

M1 = КС1 + Sk.s. (Rk xFk + Mk) = KC1 + XieNo (Ri-1 x F-1 + Mt-i) = 0_ и запишем его проекции на ось Oz. Для этого представим вектор R— в виде R-_1 = Lt-1X1, где L-_1 - координата на оси O1X1 точки О— подвеса ноги к корпусу. Тогда с учетом (41), (44) получим

M1 = Kc1 + Eie^o [Li-1X1 x (W--1 -F-) + W_1 + Lqty- xF-]=0, т. е.

M 1 =K + X_ieNo (L qt y i — L t-1 X 1 ) xF-=0,                                           (46)

— —  „      —  —P   —a                         _ где K = KC1 + LiENo [Lt-1x1 x W-^ + Wi-1]. Проекция уравнения (46) на ось Oz с учетом (39) имеет вид z^M1 = z^K + XiENo (Lqiyt — Li-1X1) x (Fxtx + Fyty) • z = 0.

Отсюда получим скалярное уравнение

S ie^o (L Xi F xi + L yi F yi ) = K ,                                                               (47)

где K = —z • K,

^L qi = ^(L qi ^y i ^{— L} i-1 ^X 1 ^{) x x} • ^z = ^(L qi ^y i ^{— L} i-1 ^X 1 ⁾ • ^(—y) = ^L i-1 ^y x1 ^{— L} qi ^y yi ,

Lqi = (Lqiyi — Li-1X1) x y • z = (Lqiyi — Li-1X1) • x = Lqixyi — Li-1Xx1, yx1 = У •X1, xx1 = X • X1 - направляющие косинусы корпуса в ССК ОП O'Xy.

Этап 9 . Для вычисления динамических реакций F_x3, F_y3, F_xS, F_yS в точках О₃ и O_s имеем два уравнения (43) и уравнение (47), из которых получим

F x3 = W x — Fx„ F y ₃ = wv—F y ₃,                                               (48)

• ^Lx 3 ^F x3 ^{+ Ly} 3 ^F y3 ^{+ L} q5 ^F x5 ⁺ L^ yS = ^Lx q3 ^(W x ^{— F} x3 ) ⁺ ^з^У ^{— F} y^ ) ^{+ L} q5 ^F x5 ^{+ L}q5 ^F y5 = x _i_ И7^р -L^rx xx .^          Ух

= ^L q3 ^W x ^{+ L} q3 ^W y ^{+ (L} qS ^{— L} q3 ^)F xS ^{+ (L} qS ^{— L} q3 ^)F yS = ^K.

Из последнего уравнения с использованием обозначений x    jx       —                        rx       1У u/P

• ^L xq = ^L qS   ^L q3 , ^L yq = ^L qS   ^L q3 , ^W a = ^{K L} q3 ^W x   ^L q3 ^W y

получим одно линейное уравнение с двумя неизвестными реакциями

LxqFxS + LyqFys = Wa.(49)

Недостающее уравнение можно получить несколькими способами. Здесь рассмотрим два из них.

Первый связан с использованием модели Кулона (7).

С учетом модели Кулона F_xS = fF_yS, F_xS< f₀F_yS уравнение (49) примет вид

(fLxq+Lyq)Fy5 = Wa.(50)

Отсюда для вычисления динамической реакции F_yS получим искомую формулу

Fy3 = Wa/(fLxq + Lyq).(51)

Остальные динамические реакции вычисляются по формулам (48). По формулам (42), (45) вычисляются искомые движущие силы и моменты сил в КП ног, т. е. последовательность расчетных формул имеет вид

F ys = W a /(fL xq + L yq ), F y3 = W y ^P - F y ₅, F xs = fF ys , ^F x3 = W x — fF y ₅,

• ^F 3 = ^W y3 ^{+ X} y3 ^F x3 ^{+ y} y3 ^F y3 , ^F S = ^W y$ ^{+ X} yS ^F xS ^{+ y} y5 ^F y5 ,

M₂ = W ^ - L q3 (X x3 F x3 + y x3 F y3 ), M₄ = W₄^Z - L q ₅(X x ₅F x ₅ + y xs F ys ).

Для реализации шага без проскальзывания ноги относительно ОП в точке О5 необходимо выполнить условие

F xs = W x — F x3 = W x — fF y3 < f o F ys = f o (Wj - F y3) ,

• т. е. W_x - f₀W_y^p<(f- f_o)F_y3 = (f- f₀)(W_y^p - F_y5) = fW ? - f₀W^p - (f - f_o)F_yS. Отсюда первое искомое условие реализации шага имеет вид

Wx-fWp <(fo-nFyS.(52)

Для реализации шага без проскальзывания ноги относительно ОП в точке О₃ необходимо выполнить условие F x3 = W x - F x ₅ = W x - fF y ₅< f o F y3 = f o (W j - F ys ).

Отсюда второе искомое условие реализации шага имеет вид

Wx-foWp <(f-fo)Fys.(53)

С целью верификации неравенств (52), (53) просуммируем их. Тогда получим

2W x -(f + f oWy ^P<  0.

Отсюда имеем

W<<(f + fo)Wp/2,                                _(54)

где по обозначению, принятому на этапе 5, W_x = х • Е у- m_o j W_C j - проекция на ось Ох абсолютного ускорения ЦМ ШМ, W ^ = Р + у • Е у— m_o j W_C j - сумма веса ШМ и проекции на ось Оу абсолютного ускорения ЦМ ШМ. Можно считать, что (f + f_o)/2 - усредненный коэффициент трения скольжения. Таким образом, неравенство (54) соответствует модели Кулона для движения ЦМ ШМ под действием сил трения, действующих на ноги.

Для применения второго способа необходимо, чтобы приводы ВКП имели обратимые редукторы. Тогда, отключив один из двух приводов, например, привод ВКП(4), получим согласно (45) М ^ = W^ - L_q5(x_x5F_x5 + y_x $ F_y3) = 0. Теперь вместе с уравнением (49) для вычисления двух динамических реакций имеем два уравнения, что и требуется для снятия неопределенности. Фактически так снимается неопределенность в распределении движущих моментов сил между приводами ВКП двух ног. Конечно, если мощности привода одной ВКП недостаточно для реализации рассматриваемого шага, то второй способ снятия неопределенности невозможен.

Заключение

В статье описан формализм решения первой задачи динамики ШМ, т. е. вычисления движущих сил и моментов сил в КП ног, обеспечивающих заданное движение корпуса и ему соответствующее движение опорных и переносных ног, где опорные ноги не проскальзывают относительно ОП. Расчет вновь создаваемых конструкций различных управляемых машин начинается с решения первой задачи динамики. Затем решают вторую задачу динамики и различные задачи управления ходьбой. Поэтому важно безошибочно и максимально точно решать именно первую задачу динамики, например, не ограничиваться моделями ШМ с ногами, массы которых сосредоточены в точках их подвеса к корпусу. Важно также верифицировать все расчетные формулы. Аналитическую верификацию мы продемонстировали на последнем примере. Многочисленные примеры численной верификации формул приведены в учебном пособии [13].