Формализмы абстрактной алгебры и полисемия экономических терминологизмов

Вычислительная математика и численный анализ представляются студентам-экономистам словосочетаниями из параллельного мира. Чем иным может заниматься математика, кроме вычислений? Не меньшее изумление возникает при упоминании безусловно практической направленности абстрактной алгебры, которая воспринимается, как нечто из далекого прошлого, что совершенно не соответствует действительности [1, с. XV]. Более того, абстрактная алгебра позволила применить всю мощь современной математики там, где о вычислениях и думать-то не могли – в науках об обществе, среди которых достойное место занимает весь комплекс экономических наук. Соответствующие изменения предлагается провести и в отношении школьного курса математики [2].

Именно абстрактная алгебра поставила в центр рассмотрения не сами объекты, а отношения между ними [3,стр.13]. Исключительную значимость этой новации подчеркивает почтенный возраст дискуссии о природе математических абстракций, характере и пределах обобщения вычислительных процедур, допустимости напрашивающихся при этом трансференций смыслов и значений. Достаточно упомянуть «universalrule» Декарта и «generalrule» Ферма [4, с.414].

Таблица 1

Фрагмент матрицы синонимов термина «profit»

earnings	gain	lucre	net	payoff	proceeds	return
a	b	c	d	e	g	h
income	accretion	bucks	earnings	earnings	earnings	earnings
incoming	accrual	cash	gain	gain	gain	gain
profit	addendum	change	lucre	lucre	income	income
gain	addition	chips	net	net	lucre	lucre
proceeds	augmentation	coin	payoff	profit	net	net
return	boost	currency	proceeds	proceeds	payoff	payoff
revenue	expansion	dough	return	return	profit	profit

Настоящим открытием для студентов-экономистов оказывается имманентное единство вплоть до сущностного совпадения лексико-семантического комплекса «рациональность-логичность» [5, с. 77]. Разумеется, их представления о «правильности» мышления замыкаются исключительно на второй элемент того, что воспринимается ими как дихотомия.

Следующая интеллектуальная встряска поджидает неокрепшие юные души на этапе, который президент России В.В. Путин назвал «цифровая экономика» (английский вариант – digitaleconomy). Оказывается, существительное «digit», от которого образовано прилагательное, революционизирующее эту самую экономику, – базовый компонент теперь уже легендарного «bit»-а.

Но тогда и логика должна быть цифровой. Более того, в этом контексте абсолютно логично, ма-тематично, просто прилично выглядит выражение «5 + 7 = 4» – в буквальном смысле детский лепет для современного ученика четвертого класса, который и не подозревает, что знаком с модулярной арифметикой [6, с. 16].

Учитывая все вышесказанное, рассмотрим в качестве примера лексико-семантический объект «profit» [7] и своего рода нейросетевое (в общем случае многомерное) пространство ассоциируемых с ним терминов.

Использование материала английского языка оправдано наличием в отечественных учебниках большого числа аббревиатур, которые не раскрываются и не переводятся. Таким образом, автор данного материала – учитель английского языка (помимо прочего) с 47-летним стажем усиливает лингвоориентированную мотивацию студентов.

Рассмотрим приводимый толковым он-лайн словарем синонимичный ряд термина «profit», расположив соответствующие им синонимы (табл. 1).

С теоретико-множественной точки зрения указание соответствующих множеств списком

(в столбцах таблицы 1) есть экстенсиональное определение данного множества [8, с. 1].

Представление матричных структур ориентированными графами (далее – орграфами) воспринимается студентами как разумная («rational») формализация, не требующая специальной алгебраической подготовки.

Скриншот орграфа свободно распространяемого программного продукта VisiGraph демонстрирует соответствующую ситуацию (рис. 1)

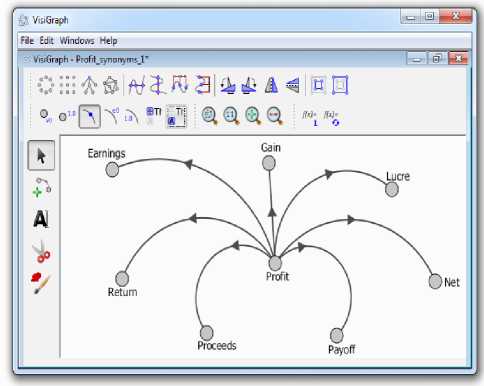
Рисунок 1. Ориентированный граф компонентного состава термина «profit»

Столь же органично воспринимается визуализация посредством орграфов межкомпонентных отношений элементов столбцов таблицы 1 (рис.2).

Матричная ситуация термина «gain», например, демонстрирует минимальный вариант входа-выхода ориентированных дуг. Фиксация всех представленных в таблице 1 отношений орграфами в принципе возможна, но быстро приводит к лавинообразному росту стрелок, делая осмысленный («rational»)анализ-синтез практически невозможным, не говоря уже о переводе больших массивов данных в машиночитаемые тексты.

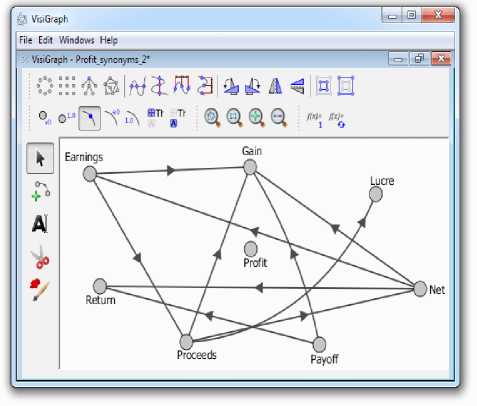
Рисунок 2. Фрагмент межкомпонентных отношений

По хорошо знакомой студентам из школьного курса информатики (7 класс) схеме «есть-нет», «истина-ложь», «включен-выключен» заполняется матрица смежности вершин орграфа (таблица 2), которую приводим в конспективном виде, опуская совершенно необходимые, но нерелевантные для целей данного материала фазы документирования алгебраических обстоятельств.

Ситуация рисунка 2 приводит к необходимости интенсионального определения выделяемых подмножеств [9, с. 1] и формирования матрицы инцидентности, с фиксацией направлений дуг (ребер) орграфа (таблица 3).

Таким образом, студенты прошли все этапы формализации и ни на одном из них не возникали отрицательные коннотации, связанные с этим термином. Более того, говорить что-либо «своими словами» в процессе конструирования содержания ячейки в таблице или именования вершины графа не приходилось потому, что на каждом шаге обучающийся видел, куда двигаться дальше, что проговаривать и т.д. Простота и очевидность оборачивались доступностью, которая трансформировалась в уверенность.

Lingua mentis становился родным, близким русским, китайским, удмуртским и далее по списку.

На заключительном этапе процесса оцифровки использовался некоммерческий программный продукт Logic Friday, позиционирующийся как «Free software for boolean logic optimization, analysis, and

Таблица 2

Матрица смежности вершин орграфа по таблице 1

	earnings	gain	lucre	net	payoff	proceeds	return
	a	b	c	d	e	g	h
a	1	0	0	1	1	1	1
b	0	0	0	0	0	0	0
c	0	0	0	0	0	0	0
d	1	0	0	0	1	1	1
e	1	1	1	1	0	1	1
g	1	1	0	1	1	1	1
h	1	1	0	1	1	1	1

Таблица 3

Фрагмент матрицы инцидентности

earnings gain lucre net payoff proceeds return a b c d e g h a b c d +1 -1 -1 e +1 -1 -1 g +1 -1 -1 -1 h +1 -1 -1 -1 synthesis». Предварительно студентам демонстрируется набор логических функций Microsoft Excel, что приводит их в полное замешательство. Они-то были уверены, что логика это о том, как правильно мыслить, а не о том, как точно и скрупулезно производить повседневные рутинные операции с огромными массивами цифровой информации, предоставляя по мере надобности необходимые рекомендации лицу, принимающему решения.

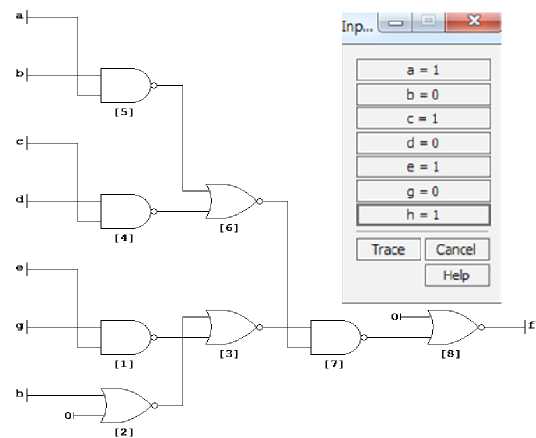
Приводимые ниже скриншоты выполнены в черно-белом варианте, хотя реальная трассировка вентильных схем происходит с выделением участков репрезентирующих включенные биты красным цветом. Здесь некоторые из них выделены штри- ховыми линиями. На практике включение-выключение сопровождается мгновенным изменением соответствующих участков логической цепочки, что подчеркивает важность тщательного предварительного документирования полисемантических комплексов экономических терминологизмов именно как носителей смыслов, в том числе и юридически соотносимых.

Первый скриншот иллюстрирует ситуацию вовлеченности каждого из приведенных выше синонимов в формирование семантического инварианта дезигната «profit» (таблица 4).

Следующая таблица – все биты комплекса «profit» выключены (таблица 5).

Таблица 4

Все биты комплекса «profit» – включены

“a”– earnings

“b” – gain “c” – lucre

“d” – net

“e” – payoff

“g” – proceeds

“h” – return

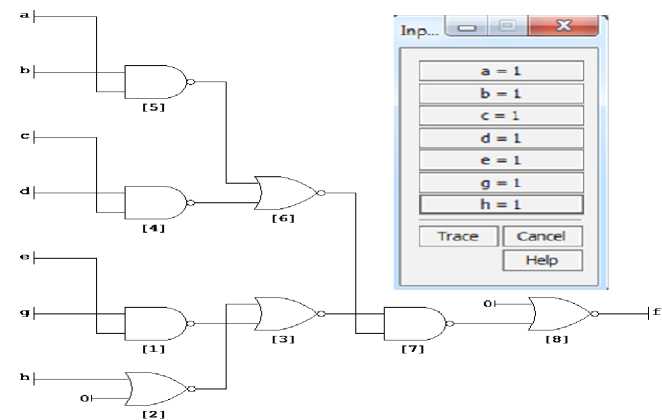
Таблица 5

Все биты переведены в состояние «нет»

“a”– earnings “b” – gain “c” – lucre “d” – net “e” – payoff “g” – proceeds “h” – return

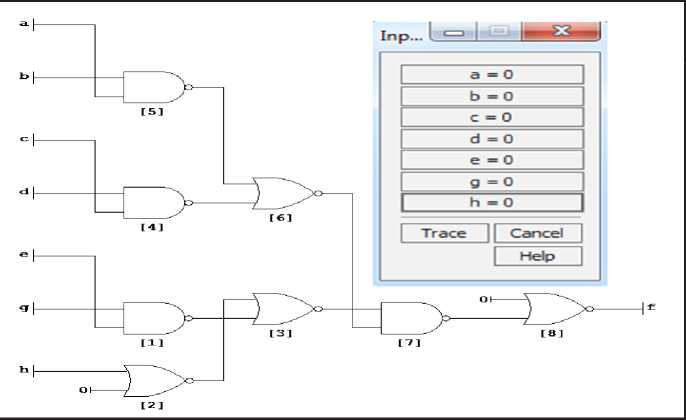
Таблица 6

Чередование двоичных разрядов

“a”– earnings “b” – gain “c” – lucre

“d” – net

“e” – payoff “g” – proceeds “h” – return

Причем эта, как и другие многочисленные не отраженные здесь схемы создаются и анализируются исключительно в дидактических целях, чтобы продемонстрировать исключительную прагматичность абстрактно-алгебраических концепций. Пример на все времена – легендарная фраза академика Щербы Л.В.

Наконец, включена только часть «битов» (таблица 6).

Таким образом, абстрагирование воспринимается студентами не как отбытие в заоблачные выси, а как собственноручно реализуемый процесс вычленения, отграничения, обособления и, в конечном итоге, перемасштабирования графемно-морфемных носителей смысла, задействуя при этом зрительный анализатор в качестве полноправного участника аналитической работы.