Формально-технологические модели в общей теории систем

Институт проблем управления сложными системами РАН, г. Самара

В статье рассматриваются методы представления моделей объектов и систем, заключающиеся в расширении концепции алгебраической системы на предельно широкий класс объектов, включая объекты физической природы, и базирующиеся на объектно-ориентированной парадигме.

Наиболее общий подход к построению моделей самых различных систем (физических, технических, биологических, социальных и т.д.) обычно связывается с общей теории систем (ОТС). Первые достаточно ясные формулировки такого рода задач восходят к работам основателей ОТС - Людвига фон Берталанфе [1, 2], Норберта Винера [3] и Росса Эшби [4], хотя некоторые идеи, ведущие к ОТС, встречаются и в более ранних публикациях других ученых, - в частности, в работах А.А. Богданова [5,6]. Имя Норберта Винера часто также связывают с основанием кибернетики, или (по определению самого Винера) с наукой об управлении в животном и машине. Тем не менее , в его наиболее известной работе [3] рассматриваются не только вопросы управления, но и некоторые общесистемные проблемы, в частности, высказывается много интересных суждений о перспективах использования математического аппарата теории групп для анализа и описания различных физических, биологических и искусственных систем, подчеркивает важность такой общесистемной концепции, как развертка (процесса или объекта) - будь то в телевидении или в организации вычислений, дается математическое обоснование концепции информации, отмечается важная роль обратной связи в ОТС, и т.д.

Росс Эшби в аналогичной работе [4], имеющей к тому же схожее название "Введение в кибернетику", излагает основы математического аппарата для исследования и описания систем вообще - как дискретных, так и непрерывных. В качестве центральных понятий при описании различных систем Эшби использует понятия операнда, оператора, преобразования, перехода и состояния, а основной концепцией представления системы является процесс ее изменения при переходе из одного состояния в другое под действием различных (внешних и внутренних) факторов. Много внимания в работе уделено понятию «свойства», под которым Эшби прежде всего понимает особенности поведения системы, в том числе особенности (свойства) математических структур, их представляющих. Значительное место в работе посвящено концепции «эмерджентных» (то есть новых, неожиданных, «появляющихся») свойств систем [4, раздел 6/18]. Отмечается, что концепция эмерджентного свойства «никогда еще не была определена точно». Далее Эшби фактически определяет эмерджентное свойство как свойство, которое не может быть нами заранее предсказано (до момента его появления) из-за неполного знания физики процессов или из-за невозможности анализа всех частей системы вследствие ее слишком высокой сложности (или чрезвычайно больших размеров) или по каким-либо иным причинам [4, с.111-114].

Следующий исторический этап в развитии ОТС часто связывают с именами Месаровича и Такахары [7]. Они формально определяют систему S , заданную на семействе множеств { V : i е I} ( I - множество индексов), как некоторое собственное подмножество декартова произведения множества { V : i е I }:

Sс х {V; еI}, (1)

причем все компоненты декартова произведения x V . называются объектами системы S [7, с.15].

Понимая ограниченность своего базового подхода, выраженного в формуле (1) и приводящего часто к чрезмерному упрощению картины, авторы с целью создания возможности для построения какой-либо теории предлагают наделить систему (1) «некоторой дополнительной структурой», а именно (цитируется по [7, с.17]):

• (i)    ввести дополнительную структуру для элементов объектов системы, скажем, рассматривать сам элемент v е V _t как некоторое множество с подходящей структурой ;

• (ii)    ввести структуру непосредственно для самих объектов системы V , i е I .

Первый путь приводит к понятию (абстрактных) временных систем, а второй - к понятию алгебраической системы (выделено мной - С .К.). Отметим, что согласно [8, с.46], алгебраической системой называется тройка U=< A , Q F , Q _P >, где A - основное множество системы U; Q F - множество операций, определенных на A и Q P - множество предикатов, заданных на множестве A .

Далее авторы рассматривают только один из вариантов развития концепции (1)-(i), именно тот, который они определили как временные системы, то есть такие, в которых элементами одного из объектов системы являются функции времени. Возможные пути развития концепции (1)-(ii) при этом почти никак не оцениваются и ограничиваются лишь примером алгебры над всеми возможными словами из алфавита W z V с бинарным отношением R : V x V ^ V , то есть с операцией сочленения слов. Согласно тому же источнику [8, с.47], алгеброй называется двойка U=< A , Q _F >.

Как и в работах Р.Эшби, термин «свойство» трактуется в [7] достаточно неформально, то есть в него вкладывается именно тот смысл, который сами исследователи обнаружили в предлагаемых ими математических моделях изучаемых феноменов, и который они интерпретируют именно как свойство, а не как математическую закономерность, присущую их модели.

На проблему адекватного представления различных свойств в различных математических конструкциях, представляющих системы, обращают внимание многие ученые - в том числе и Роберт Розен. Он, в частности, пишет о существовании двух принципиально разных наборов свойств систем, изучаемых в ОТС, во-первых, свойств, проистекающих из физичности объектов исследуемой системы, которые, как правило, никак не представлены в существующих формальных описаниях, и, во-вторых, свойств, связанных с логическими (т.е. математическими) свойствами самой системы, которые можно «вычислить», анализируя формальное математическое представление [4, 9,10]. В значительной степени обосновал правомерность такой точки зрения и на многих фактических примерах продемонстрировал неэквивалентность этих двух разновидностей системных свойств Георгий Кампис [11].

Одной из первых попыток как-то формализовать концепцию свойств системы (объекта) можно считать попытку Дж. Клира [12]:

Определение 1. Под системой объекта понимается любой (абстрактный или реальный) объект O , представляемый следующим образом:

O = ({(а, A )| е N n }, { b j , B . | je N }), (2) где N n = {1,2,..., n }; N m = {1,2,..., m}; a . - свойство объекта; A_i - множество проявлений свойства a. ; b. - база (т.е. любое существенное свойство, “... на самом деле используемое для определения различий в наблюдениях одного и того же свойства” [12, с.45]); B j - множество элементов базы.

В связи с разрабатываемой им концепцией Дж. Клир делает также ряд чрезвычайно интересных замечаний. Во-первых, он подчеркивает известную оторванность «чистой математики» от реальности, отмечая, что она «...занимается в основном разработкой разных аксиоматических теорий независимо от того, имеют они практическое значение или нет..., и не ее цель определять, существует ли некая интерпретация теории, для которой эти (исходные) предположения истинны» [12, с.28].

Во-вторых, он подчеркивает явную тенденцию современной науки к обобщению, объединению различных парадигм [12, с.31].

В третьих, он особо выделяет роль вычислительной техники не только в качестве стимулирующего фактора, но и как своего рода симбиотического фактора, без которого развитие ОТС практически немыслимо, а также как фактора, поставляющего и генерирующего для ОТС новые концепции и методы, в частности, в плане расширения общесистемного понимания термина «архитектура», как самого верхнего уровня организации любой системы [12, с.39].

Среди других авторов, в большей или меньшей степени использующих математические методы при построении своих концепций ОТС или близких к ней научных направлений, следует отметить работы ГХакена [13], И.Пригожи-на, Г.Николиса и И.Стенгерс [14, 15], Г.Вунша [16], М.А.Арбиба, Р.Калмана и П.Фалба [17], О .Ланге [18], В.М.Глушкова [19], Н.Н.Моисее-ва [20], В.Н.Садовского [21], Н.П.Бусленко [22], В.В.Дружинина, Д.С.Конторова [23], Ю.А.Ш-рейдера, А.А.Шарова [24] а также ряд других [25,26].

Особо выделим работы О.Ланге, поскольку он в своем подходе к ОТС значительное внимание уделяет концепции элемента системы, отмечая следующее: 1) среда действует на элемент (через температуру, давление, электрический заряд, ощущения и т.д.), вызывая в нем некоторые состояния, отдельные виды которых называются входами, 2) элемент действует на среду, принимая некоторые состояния определенного рода, отдельные виды которых называются выходами, 3) элемент имеет, по крайней мере, один вход и один выход, 4) состояние входов элемента однозначным образом определяет состояние его выходов, причем состояния и входов, и выходов описываются с помощью чисел [18, с.184]. На основе этой концепции определяются векторы состояний входов и выходов элементов, операторы прямой и обратной трансформации, матрицы связей входов одного элемента с выходами другого, матрица структуры системы, граничные и внутренние элементы, поверхность системы, способ ее действия и др., в результате чего получается формальное представление системы, вполне согласующееся с концепциями Р.Эшби, Месаровича, Такахары и Дж.Кли-ра.

Наибольший интерес в качестве возможных альтернативных подходов к ОТС представляет собой предложение Шрейдера и Шарова использовать теорию категорий. Суть предлагаемого ими подхода заключается в том, что алгебраические модели (т.е. множества с отношениями) рассматриваются «как воплощение формальных теорий» [24, с.22]. При этом формально модель Mзаписывается как: M = , где M - некоторое множество, ri - отношения на М как подмножества декартовых произ ведений элементов M. Затем вводятся понятия сигнатуры Q для модели M, теории T = , где {Ф} - аксиомы, {р} - множество правил вывода; и каркаса:

K=<, Q2, A >, (3)

где - модель в сигнатуре Q 1 , а - инъективное отображение из Q 1 в множество всех возможных отношений на M (разной местности), Q 2 - сигнатура, не имеющая общих имен отношений с Q_p A = { A 1 ,..., A n } - аксиоматика, использующая имена отношений из Q 1 и Q 2 . Состоянием каркаса K=<, Q₂, A > называется модель в сигнатуре Q 1 uQ₂, при этом функции а и в совпадают на Q 1 и выполняется аксиоматика A . На основе концепции каркаса (3) и его состояния и вводится, собственно, формальное определение системы 2:

Определение 2. Системой 2 будем называть класс каркасов, между состояниями которых определены морфизмы [24, с.73].

В определении 2 в первую очередь обращает на себя внимание тот факт, что несмотря на критику теоретико-множественного подхода к ОТС, авторы вынуждены все-таки остаться в его рамках, сменив, по большому счету, лишь форму представления компонентов и связей между ними в системе. Действительно, как и чисто алгебраический подход Месаровича и Такахары, так и концепция моделей Шрейдера и Шарова базируются на одном и том же фундаментальном математическом понятии - теоретико-множественной конструкции алгебраической системы, представляя в ней две крайних формы: алгебры, как совокупности некоторого множества элементов и операций над ними, и модели, как совокупности некоторого множества элементов и предикатов над ними. И операции, и предикаты могут быть заданы в виде отношений между элементами множества [8, с.46-48].

К аналогичным попыткам выйти за рамки классического подхода и детально проанализировать возможности концепции (1)-(ii) Месаро-вича и Такахары, а также в определенном смысле объединить и расширить методы формального представления объектов (элементов систем) и их свойств, заявленные Дж.Клиром, О .Ланге и рядом других ученых, можно считать подход, заключающийся в расширении концепции алгеб- раической системы на предельно широкую область объектов, включающую не только абстрактные, но и реальные объекты (в виде соответствующих математических моделей) самой различной природы, в том числе и объекты абсолютно разнородного (гетерогенного) характера [27-29]. Следует особо подчеркнуть, что именно отсутствие математических методов, позволяющих эффективно работать с разнородными (гетерогенными) объектами, выделяется Г.Кам-писом как основной недостаток существующих математических методов ОТС [11].

Суть предлагаемого подхода, получившего название формально-технологического, заключается в том, что любое (в том числе гетерогенное) множество объектов с операциями над ними определяется как некоторая формальная технология:

Определение 3. Под формальной технологией T понимается упорядоченная пара < A, F >, состоящая из двух конечных множеств: множества A некоторых исходных типов элементов (объектов) материальной или нематериальной природы, называемых обычно элементами базы (или базовыми элементами): A = { a 1 , a 2 ,a 3 ,..., a n }, и множества операций F над элементами базы и (или) элементами, полученными в каких-либо операциях T : F = {F 1 ,F₂ ,...,F_m}, причем ни одна из операций в F не может быть выражена через другие.

Однократное применение операций из F к элементам из A или конструкциям, полученным ранее из элементов A и (или) других конструкций, принято называть шагом технологии T .

Примерами множеств A могут служить некие аналоги атомов («квазиатомы»), наборы различных химических веществ, отрезки аналоговых сигналов, компоненты различных систем, какие-либо абстрактные объекты, в том числе объекты информационного характера - числа, коды и/или символы, и т.д., и т.п. [27,28].

Обычно в F выделяются собственно «технологические» операции F (синтеза, декомпозиции, дезинтеграции, сложения, вычитания, умножения объектов, и т.д.), и так называемые аналитические операции P, являющиеся «технологическими» аналогами предикатов в математических структурах и конструкциях, например, операции сравнения двух объектов, определения цвета, веса, длины, формы, pH объекта и т.д. и т.п. Первую группу операций F можно отождествить с операциями QF, вторую - с операциями QP в классическом определении алгебраических систем U=. Таким образом, в общем виде определение формальной технологии явно тяготеет к определению алгебраических систем, что делает вполне естественным и весьма эффективным использование при анализе различных ФТ-моделей не только аппарата самих алгебраических систем, но и смежных направлений математики, в первую очередь, теории алгоритмов, теории вычислений и рекурсивных функций [27, 28]. Одновременно следует подчеркнуть, что один из наиболее популярных подходов к ОТС, основанный на теории групп [3, 19], в ФТ-контексте выглядит менее привлекательным, поскольку соответствует лишь усеченному варианту ФТ-моделей, а именно, технологиям без аналитических операций, эквивалентных в математических структурах алгебрам U=.

Важной особенностью полных ФТ-моделей типа T=, в отличие от математических алгебраических систем, является наличие нескольких эквивалентных наборов аналитических операций P (то есть нескольких эквивалентных предикативных систем типа QP). В [27], в частности, показано, что такими эквивалентными наборами могут быть P0={Pe(xy)}, Pi ={Р(x,u)}, P2 ={Pri(xR), Pr2(xR),..., PJx,Rn)}, P3 ={Pa(x)}, а также ряд других наборов, причем здесь Pe(x, y) - операция (предикат) определения равенства двух объектов: Pe(xy)=1, если x=y, и: Pe(x,y)=0, если x*y; Pu(x,u) - операция сравнения с так называемой «представительной» конструкцией (содержащей в себе все типы элементов базы, кроме, быть может, одного): Pu(x,u)=1, если x=u, и Pu(x,u)=0, если x^u; PRi(x,R.) - операция сравнения с i-ой из n представительных конструкций, содержащих в совокупности все элементы базы (кроме, быть может, одного); Pa(x)^e -операция так называемого «случайного стационарного отображения», отображающая некоторое (возможно даже неизвестное) свойство анализируемого объекта на числовую ось с помощью опять же некоторого неизвестного механизма [27, с.55], что делает эту операцию похожей на операцию, выполняемую оракулами в расши- ренной концепции вычислений А.Тьюринга [30]. Последняя в последнее время широко дискутируется в связи с возможностью т.н. «гипервычислений» [31].

Для унифицированного представления различных (в том числе разнородных, т.е. гетерогенных) объектов с различными наборами свойств и различными типами собственных фун-кциональностей вводятся следующие определения:

Определение 4. Свойство объекта (или конструкции, т.е. системы объектов) - это некоторая числовая, геометрическая, физическая или любая другая, в том числе воображаемая, его характеристика, стабильная при определенных стабильных условиях, по которой (по которым) объекты и (или) конструкции могут отличаться друг от друга или от своего предшествующего во времени и/или пространстве состояния.

Определение 5. Состоянием объекта (конструкции) называется совокупное конкретное значение всех его свойств .

Определение 6. Свойство (объекта или конструкции) называется функциональным, если оно позволяет изменять состояние объекта при физическом сближении или соединении соответствующих объектов - носителей свойств .

Определение 7. Эмерджентным называется такое свойство объекта x (с непустым значением), которое отсутствовало на предыдущих шагах технологии в объектах, из которых был получен объект x .

Таким образом, любой элемент базы а. (как и любой объект) в формальной технологии может быть представлен математической моделью в виде совокупности двух множеств: а.==<{Y«. Yr- Yn}, {у=oj (Уя-у,);-; y,=фГ (y/' Y„,)}>. где Yp - список параметров fro Y,r- Yn} отображающих свойства данного элемента а на числовую ось (или на другую, заранее оговариваемую, нечисловую шк алу), м„={7,=Фj(Ys— Y)’";' Yr=ф,«Y„)} - список функциональностей, относящихся к этим свойствам. Состояние элемента а. - это конкретное значение всех параметров Ypi - то есть конкретное значение соответствующего вектора ri. В общем виде для моделей объектов предполагается, что любая его функциональность может быть задана подходящей частично-рекурсивной функцией, то есть является вычислимой, хотя в особо оговариваемых случаях это может быть и не так - как и, например, для операции «случайного стационарного отображения».

Рассмотрим в качестве примеров две функциональности: функциональность логического элемента «2-И-НЕ» и некую химическую функциональность, приводящую к химической реакции между двумя веществами.

Для логического элемента, представленного на рис. 1 (как гомогенного элемента E 1 различных логических схем) имеем:

^E i =Mi> = ^7 ■ Y?Уз^{} {}Уз=О'Y- 7 7- I⁴ где в списке свойств указаны только три интересующих нас в данном случае свойства (параметра): Y1, Y₂, Y₃, причем yie {0,1}, а в списке методов имеется только один метод: Уз О.⁽Y_PY2⁾⁼l(Yi&Yz) (1 - символ инверсии).

Теперь обратимся к некоей абстрактной химической реакции между двумя веществами а и b (гетерогенными по своим свойствам), итогом которой является новое вещество - с (пример взят из [32], с.192):

а + b ^ с. (5)

По условиям вещества а и b , также как и вещество с , имеют свой набор физико-химических свойств, которые могут иметь (или не иметь) отображения на различные числовые характеристики («параметры»). Таким образом, участвующие в реакции объекты отвечают определениям 4-6. То, что после оеакции исходные объекты а и b перестали существовать, не имеет принципиального значения, поскольку в условиях определения 6 нет указаний на необходимость их сохранения. Более того, для более формального соответствия записи реакции (5) определению 6 можно считать, что объект-носитель одного набора функциональных свойств, подвергающийся воздействию со стороны некоторого другого набора функциональных свойств, это, напри-

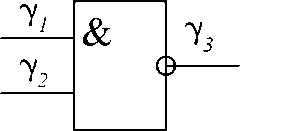
Рис.1. Логический элемент "2-И-НЕ"

мер, объект b =_b, ^Mb>=b, ^{Yc=Tab⁽Yb, Ya)^,-}^>(где функциональность ф_ab описывает преобразование свойств Y_b, Ya в свойства Yc); носитель другого набора функциональных свойств Ya -объект a=_a, Ma>, и в результате химического взаимодействия (реакции) между объектом b (с его набором свойств) и свойствами объекта a объект b меняет свои свойства, превращаясь в объект c с иным, нежели у b, набором свойств.

Таким образом, если объекты-элементы базы (гетерогенного или гомогенного характера) имеют свойства, способные взаимодействовать друг с другом, то они могут образовывать некоторую более сложную (совокупную) функциональную систему (конструкцию), общая функциональность которой определяется композицией имеющихся функциональностей объектов, зависящей от их пространственного расположения (в том числе возникшей в ходе «химических реакций» между объектами), а также наличия или отсутствия эмерджентных свойств (и соответствующих эмерджентных функционально-стей) у образовавшихся конструкций. Если же таких свойств нет, то объекты не могут образовать никакую функциональную систему, кроме простой суммы исходных функциональностей, присущих самим объектам.

Для примера, клеточные автоматы (КА) могут формировать различные типы поведения благодаря определенной пространственной геометрии (топологии) расположения своих клеток и наличию функциональностей, переводящих клетку в следующее состояние в зависимости от собственного текущего состояния и состояния соседних клеток [33,34]. При этом функциональные эмерджентные свойства у КА в смысле определения 7 отсутствуют. Кажущаяся функциональная эмерджентность КА, проявляющаяся в новых типах поведения, в том числе в самовоспроизведении, на самом деле есть следствие все той же (порой весьма сложной) топологии и исходного (фиксированного) набора свойств и функциональностей [33, 34]. В этой связи указанные свойства композиций функций, задаваемых соответствующей топологией и фун-кциональностями элементов систем, определяющих в итоге их поведение (их динамику), можно считать теми самыми вычислимыми математическими закономерностями, которые часто и изучаются в ОТС, как свойства систем вообще, причем параметры Ypi выступают здесь своего рода аналогами «физических» свойств объектов, определяющих характер поведения систем лишь опосредованно через соответствующие функциональности.

Необходимо подчеркнуть, что рассмотренное выше унифицированное математическое представление моделей объектов, во-первых, хорошо коррелирует с концепциями «алгебры физических взаимодействий», предложенной Е.М.Карповым [26], и, во-вторых, с идеями объектно-ориентированного программирования (ООП), что позволяет легко переносить их практически в любую компьютерную среду, поддерживающую ООП, для проведения различных модельных компьютерных экспериментов, испытаний и аналитических расчетов. Более того, формальный анализ возможных свойств и фун-кциональностей объектов в стиле ООП оказывается полезным не только при компьютерном моделировании их поведения в тех или иных технологиях, но может рассматриваться и как самостоятельный, весьма эффективный метод самой формальной технологии, позволяющий, например, сводить систему химических функциональных преобразований различных веществ к универсальному функциональному базису соответствующих наборов булевских функций и обратно [35,36].

На основе предложенной выше расширенной (формально-технологической и объектноориентированной) трактовки алгебраических систем с учетом ее тесной связи с теорией алгоритмов и рекурсивных функций - удалось построить модели универсальных технологических систем для самых различных технологий, включая технологии обработки и преобразования аналоговых сигналов, химические и машиностроительные [27-29,35,37]. В свою очередь, на основе полученных моделей универсальных дискретно-аналоговых вычислительных систем, а также универсальных систем для синтеза и анализа физических конструкций, удалось доказать ограниченность действия тезиса Тьюринга-Черча на объектах с континуальными и физическими свойствами, то есть доказать наличие своеобразных «гипервычислительных» процессов в различных физических системах

[27, 29, 31, 36, 38].

Аналогичный подход позволяет использовать общие математические методы и при построении моделей эволюционных систем, в первую очередь, биологических [27, 39]. Здесь, однако, имеются существенные пробелы в требуемом математическом аппарате, поскольку в эволюционной технологии внешние операции над объектами (элементами базы), как привило, должны быть исключены, т.е. эволюционная технология может быть задана только множеством A : T =< A > (при этом для всех элементов базы обязательно выполняются условия a_i =<γ _pi , M_fi >=<{γ _i0, γ _i1,... γ _in }, {γ _ij =ϕ _j (γ _is,..., γ _jk );...; γ _ir =ϕ _r (γ _it,..., γ _ml )}>, иначе элементы согласно приведенным определениям просто не будут взаимодействовать друг с другом). Подчеркнем, что заданные таким образом эволюционные технологии не могут быть отнесены ни к алгебраическим системам, ни к алгебрам, ни к моделям .

Таким образом, подход, получивший название формально-технологического , позволяет, во-первых, в полной мере использовать для описания множества объектов систем концепцию алгебраической системы, упомянутую Месарови-чем и Такахарой, но практически не исследованную ими. Во-вторых, он в большей степени, нежели подход Дж.Клира, ориентирован на формальное представление свойств объектов (в том числе компонентов системы и самих систем) в их формальном описании. В-третьих, он подводит прочный теоретический фундамент под высказывания многих ученых о междисциплинарном характере теории алгоритмов и теории вычислений, проясняя возможные причины достаточно общих свойств различных технологий и соответствующих систем. Наконец, в четвертых, он вводит единую для всех объектов концепцию всех типов функциональностей объектов, что делает единообразным представление самых различных (т.е. гетерогенных) объектов с точки зрения математики и позволяет рассчитывать поведение систем, состоящих из таких гетерогенных объектов. Последняя возможность недоступна (по мнению Г.Камписа) для существующих математических методов, ориентированных, в первую очередь, на работу с множествами гомогенных объектов [11].