Формфактор голограмм сложных изображений
Автор: Шойдин Сергей Александрович, Трифанов Александр Владимирович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.42, 2018 года.
Бесплатный доступ
В настоящей работе продолжается изучение влияния формфактора голограмм на их оптимальные характеристики, такие как оптимальная экспозиция при условии известного распределения видности и максимально достижимые значения средней по голограмме дифракционной эффективности. Главное внимание в работе уделено проверке применимости понятия формфактора к вычислениям оптимальных параметров фазовой голограммы. Полученные результаты позволяют утверждать, что для голограмм реальных изображений, сформированных сложными по форме пучками, применима технология вычисления и практического использования формфактора. На примере более чем 30 реальных изображений проанализирован подход к определению формфактора для изображающих голограмм. Обнаружено достаточно хорошее совпадение формфактора голограмм реальных портретных изображений с формфактором голограмм Гауссовых пучков. Показано, что реальные изображения имеют статистику распределения яркости, близкую к Гауссовой, но и для других статистик предложенный метод расчёта и использования формфактора применим.
Лазер, голограмма, формфактор, дифракционная эффективность, гауссов пучок, портрет
Короткий адрес: https://sciup.org/140228738
IDR: 140228738 | DOI: 10.18287/2412-6179-2018-42-3-362-368
Текст научной статьи Формфактор голограмм сложных изображений
При разработке новых голографических материалов большое внимание уделяется увеличению динамического диапазона фотоотклика среды [1,2]. Однако, как было показано в [3–5], использование большого динамического диапазона голографической среды для увеличения дифракционной эффективности не всегда возможно, поскольку дифракционная эффективность ограничивается влиянием так называемого формфактора голограммы. В [6, 7] для Гауссовых пучков были получены ограничения на максимально достижимую дифракционную эффективность п , а также получен коэффициент увеличения оптимальной экспозиции, требуемой для достижения её максимума, названный формфактором. Там же было отмечено, что влияние формфактора проявляется только при одновременном существовании двух эффектов – нелинейности отклика, в данном случае п m ( E , V), и неравномерности яркости по полю E ( x , y ). Несмотря на широкую применимость модели Гауссовых пучков при записи голограмм, часто распределение яркости так называемых объектных пучков по полю голограммы не соответствует форме Гауссовых кривых. Однако, как было отмечено в [7], большинство сложных по форме пучков, имеющих многофакторное (хотя и не Гауссово по полю) распределение яркости, в силу центральной предельной теоремы (ЦПТ) могут приближаться к Гауссовой статистике распределения яркости. Это означает, что для голограмм, записанных такими пучками, тоже можно ожидать подобного проявления формфактора, чему и посвящена настоящая работа.
Численное моделирование и экспериментальные результаты
В [6,7] показано, что средняя дифракционная эффективность фазовых голограмм пm(E, V), записанных неравномерными по яркости пучками, определяется выражением (1).
П m = ( | ' jJ sin 2 { Р ( E ) E ( x , У)V(x , У ) } d x d y , (1) где η m – средняя по полю голограммы дифракционная эффективность, 5 - площадь голограммы, P ( E ) -голографическая чувствительность фотоматериала, а V – видность интерференционной картины при записи. Здесь полагается, что и видность, и экспозиция могут в общем случае меняться по полю голограммы ( x , y ), а фотоотклик голографического материала – его чувствительность Р ( E) в общем случае может иметь нелинейный вид, например, как в [6].
Можно ли в случае сложных изображений, например, при записи голограммы портрета, воспользоваться, как и для Гауссовых пучков [7], вычислениями оптимальной экспозиции для достижения максимальной п m по формуле (2), предложенной для Гауссовых пучков?
п m =Q sin2 { ^ f ( EV ) } . (2)
Здесь величина Q ограничивает максимально достижимую среднюю дифракционную эффективность голограммы, а V - константа, учитывающая весовую функцию яркости при интегрировании (1). Она отражает эффективную задержку достижения первого максимума η m , приводя сложные вычисления по (1) к простым вычислениям по (2), которые аналогичны известным классическим вычислениям [8]. Использование известной, заранее вычисленной величины формфактора, в практической работе существенно облегчает отработку технологии записи голограмм.
Для численного эксперимента было выбрано типичное портретное изображение с разрешением 200×200, пригодное для размещения на документах, удостоверяющих личность. Оно было сделано фотоаппаратом Canon EOS 350D в режиме автоматического выбора экспозиции по времени. Затем полученное изображение было преобразовано стандартными методами Photoshop в изображение в серых тонах рис. 1a, распределение яркости которого приведено на рис. 1б.
б)
В серых тонах

100 150 200
О А,
200 а)
0,6?'
0,4'
В серых тонах 3D

Рис. 1. Изображение в серых тонах (а), 3D-развёртка динамического диапазона яркостей А1 составляющих его точек (б)
Можно видеть, что распределение яркости (рис. 1 б) носит как будто случайный характер. Однако его весовая функция яркости близка к Гауссовому распределению (см. pис. 2).
Типовым оператором histForPhoto в среде Matlab были построены гистограммы изображения 1 б , приведённые на рис. 2 а , б .
На гистограмме (рис. 2 а ) видно, что в кадре изображения рис. 1 а много пустого места, не занятого изображением, где яркость равна нулю. Убирая этот пик из статистического распределения, можно более подробно видеть картину распределения яркостей собственно по полю изображения портрета на рис. 2 б . Её среднее отклонение от показанной на том же графике Гауссовой кривой составляет 18 %.
Если внимательно исследовать развёртку динамического диапазона точек изображения на рис. 1 б , можно обнаружить, что самые яркие точки не дотягивают до А 1 = 1, а остаются ниже уровня 0,65, а самые тёмные образуют как бы общую полочку в районе А 1 = 0,2.
Пропорциональное растяжение динамического диапазона всего изображения так, чтобы самые яркие точки приближались к А 1 = 1, а «полочка» была удалена (для этого динамический диапазон А 1 внутри 0,2–0,65 был растянут от 0 до 1,0), не привело к существенному отклонению полученных гистограмм от
Гауссовой кривой. В этом смысле степень похожести гистограммы портрета на Гауссову кривую можно считать некоторым инвариантом относительно указанных изменений динамического диапазона. Поэто- му в дальнейшем мы будем обращаться к исходному изображению рис. 1а, б со статистическим распреде-
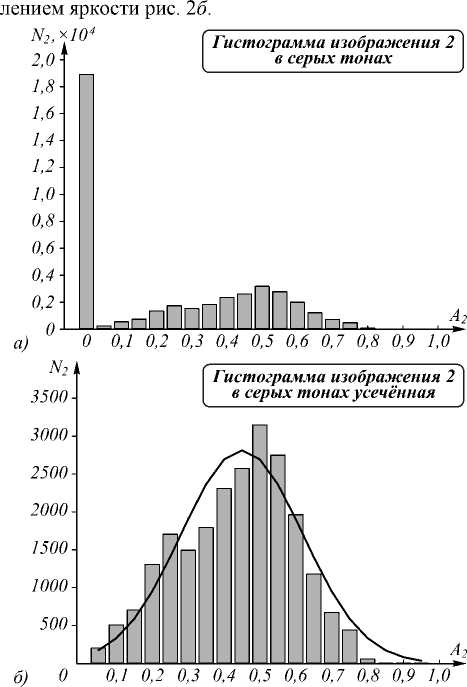
Рис. 2. Гистограммы распределения яркости: для исходного портрета 1а(1б) (а), для того же портрета с отсечённым нулевым фоном (б)
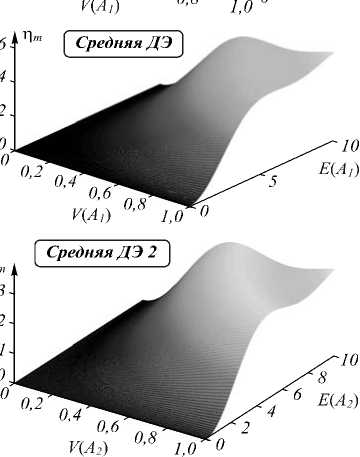
Вычисленная по формуле (1) средняя дифракционная эффективность η m ( E , V ) для портретного изображения рис. 1 а , б и средняя дифракционная эффективность η m ( E , V ) для Гауссового пучка, аналогичного [6], показаны соответственно на рис. 3 а , б . Здесь и далее мы берём для вычислений по (1) линейный фотоотклик среды ( β = 1), чтобы не усложнять анализ численных расчётов излишним количеством анализируемых параметров. Далее мы приведём некоторые результаты, полученные с учётом нелинейности фотоотклика среды, но это заслуживает отдельного, более подробного изложения.
При сравнении рис. 3 а и 3 б видно, что в первом случае колебания не нарастают при росте экспозиции (и видности) после достижения η m ( E , V ) первого максимума, а во втором, для Гауссова пучка – возрастают и значительно. В [6] такое поведение графика η m ( E , V ) было объяснено ростом вклада удалённых от центра частей Гауссова пучка, когда локальные значения аргумента под синусом (1) на периферийных участках голограммы перерастают π .
[ Средняя ДЭ j

a)
О,
О,
б)
П О,.
О,.
О,
в)
Рис. 3. Зависимость n m (E, V) для изображения на рис. 1: исходного портрета (а); Гауссова пучка (б); усечённого по уровню А ] Гауссова пучка в диапазонеА2 = (0,2 ^ 1,0) А ] (в)
Для реальных изображений ( n m на рис. 3 а ) по изображению, приведённому на рис. 1 а , б , такого роста нет. Видно, что на рис. 1 б изображение по полю обрывается круто, а не как у Гаусса с бесконечно широкими крыльями внизу. Это и есть причина основных отличий реального изображения от изображения Гауссовых пучков.
На гистограммах рис. 2 также видно, что правая их часть довольно похожа на Гауссову кривую, а левая похожа меньше и даже на каком-то значении обрывается.
Отсюда было сделано предположение о том, что статистика распределения яркостей А 1 локальных точек портретного изображения (рис. 1) похожа на Гауссову лишь частично, а в большей степени соответствует статистике распределения Гаусса усечённого, как если бы у Гауссового распределения была отсечена нижняя часть, что не позволяло бы этой части вносить свой вклад с ростом экспозиции. Для подтверждения этого подробнее рассмотрим графики П m ( E , V), приведённые на рис. 3.
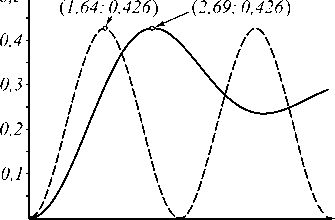
Даже на глаз видно, что двумерный график (рис. 3в) больше похож на рис. 3а, чем на график на рис. 3б. Однако удобнее анализировать двумерные сечения этих графиков. На рис. 4 приведены зависимости nm от E как сечения графиков из рис. 3 плоскостью, параллельной V для значений видности, близкой единице (V =0,951). В силу симметричной зави- симости nm как от E, так и от V, для случая линейного фотоотклика, этого будет достаточно для нахождения значений формфактора Ψ и максимально достижимой дифракционной эффективности Ω.
На рис. 4 приведены значения координат первых максимумов графиков n m ( E ) . Видно, что на рис. 4 а дифракционная эффективность голограммы под влиянием формфактора достигает максимального значения Q 1 =42,6% при экспозиции E в 2,69/1,64 = 1,64 раза большей, чем в идеальной [8] голограмме, что соответствует значению Ψ 1 = 1/1,64 = 0,61 для формулы (2). Таким же образом рассчитанные значения для Гауссовых пучков из рис. 4 б получаются равными Ω 2 = 45% и Ψ 2 = 0,55. Значения, хоть и близкие к Ω 1 и Ψ 1 , но отличающиеся по Ψ на 9,8 %, а по Ω – на 5,3 %.
П»4
а) 0 / 2 3 4 5 6 Е
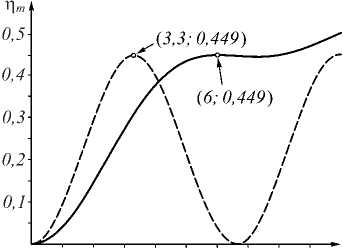
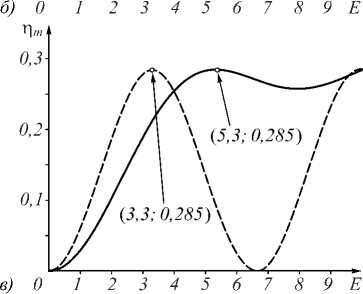
Рис. 4. Сплошная линия - зависимость n m от экспозиции E при V= 0,951: для исходного изображения (портрета на рис. 1) (а); для Гауссова пучка (б); для усечённого Гауссова пучка с модифицированным динамическим диапазоном (А2 = А ; {0,2 ^1,0}) (в). Пунктирная линия -зависимость от тех же параметров идеальной голограммы, сформированной равномерным по полю сигналом [8], уменьшенная по ординате для удобства представления до значения Q-первого максимума n m (E)
В случае усечённого снизу Гауссова пучка (0,2 ÷ 1,0) величина Ψ 3 = 0,62, т. е. становится практически равной Ψ 1 , а Ω 3 падает до 28,5 %. Уменьшение максимально достижимой дифракционной эффективности Ψ 3 объясняется просто уменьшением эффективной площади, занимаемой усечённым Гауссовым пучком на голограмме. Пропорциональным увеличением диаметра усечённого Гаусса примерно на 15% было получено увеличение Ψ 2 до 44 %.
Таким образом можно утверждать, что сделанное в [7] предположение о том, что сложные изображения, имеющие в силу ЦПТ статистически Гауссово распределение яркостей, также имеют формфактор, близкий к формфактору Гауссовых пучков, подтвердилось. Уточняя этот результат, можно сказать, что формфактор портретных изображений ближе к формфактору усечённого снизу Гаусса.
Повторяемость полученных результатов
Для проверки репрезентативности полученных результатов были проанализированы по описанной выше методике портреты группы из 31 человека.
Среди них были женщины и мужчины, снимавшиеся в очках и без очков, со вспышкой и без неё. По этой группе были вычислены средние значения формфактора Ψ = 0,6157 и дисперсии распределения яркости D = 0,3197. Среднеквадратичное отклонение формфактора при этом составляло 6,087%, а дисперсии – 32,867%. Максимальное отклонение формфактора от среднего значения по группе составило max Ψ = 0,11; а max D = 0,16. Таким образом, можно сделать вывод о том, что практическое применение формфактора при определении оптимальных условий записи (экспозиции и видности) для сложных многофакторных изображений, имеющих близкое к Гауссовому статистическое распределение яркости, можно проводить по формуле Когельника [7], но с учётом формфактора, вычисленного для (2) по (1), который равен формфактору Гауссовых пучков [6,7]. Поскольку отклонение от Гауссовой статистики было по группе из 31 человека 32%, а отклонения в формфакторе были 6,1 % (при этом сама средняя величина формфактора на случайной группе из 31 человека была 0,615), то можно сделать вывод, что даже отклонения от Гауссова статистического распределения не дают существенного изменения формфактора. Именно поэтому можно использовать полученное ранее значение формфактора для Гауссовых пучков при записи на голограмму реальных портретных изображений. Самое главное, что это исследование еще раз подтверждает, что формфактор устойчив к статистическим отклонениям в силу нелинейности под интегралом (1), таким образом стабилизируя в выражении (2) численное значение формфактора вблизи его значения для Гауссовых пучков.
Нелинейность фотоотклика голографического материала
Учёт нелинейности β(E), подобной приведённой в [7], также проводился. Численный анализ подтвер- ждает, в частности, что нелинейность снижает максимально достижимое значение ηm, но не пропорционально снижению значения фотоотклика, а ощутимо меньше. Так, для указанной нелинейности, характерной для фотоматериала «Реоксан» [1], максимальное значение фотоотклика при записи голограммы портрета (рис. 1) в точке первого максимума ηm снижается в 1,54 раза по сравнению с линейным фотооткликом. В то же время сама дифракционная эффективность ηm уменьшается только в 1,38 раза. Это указывает на то, что нелинейность фотоотклика голографической среды работает в том же направлении, что и появляющаяся за счёт нелинейности дополнительная компонента линейного отклика [8, стр. 381]. Однако более тонкие эффекты связи нелинейности фотоотклика и отличия статистики распределения яркости пучков от Гауссовой формы выходят за рамки настоящей работы и будут рассмотрены в дальнейшем.
Обсуждение
Полученные в настоящей работе результаты говорят о том, что сложные голографические изображения, формирующиеся с помощью пучков, чья неоднородность по полю является следствием наложения влияния многих факторов (отражение, поглощение, дифракция и другие виды рассеяния излучения), создающих реальную картину окружающей среды, обладают статистическим распределением яркости интерференционной картины близким к Гауссовому. Оптимальная экспозиция для таких голограмм, с учётом видности интерференционной картины, может быть рассчитана с помощью формфактора.
Степень точности таких расчётов определяется:
– Во-первых, близостью статистики распределения яркости описанных с помощью формфактора изображений к эталонной статистике, используемой в расчёте. В нашем случае отличие гистограмм изображения и ближайшей к ним Гауссовой кривой составляло 18 %, а отличие в величине формфактора между ними ( ψ 1 и ψ 2) не превышало 10%. При правильном подборе описывающей изображение статистики (усечённый на 20% снизу Гаусс) отличия в формфакторе между ψ 1 и ψ 3 составляли всего 1,6%. Такой точности вполне достаточно для практического выбора экспозиции при известной величине видности записывающей голограмму интерференционной картины.
– Во-вторых, степень точности расчётов определяется пропорциональной долей сигнала с определённой статистикой в общем кадре. Так, ограничивая Гаусс снизу отсечением его значений, лежащих в диапазоне яркостей от нуля до 20%, мы тем самым уменьшили вклад бесконечно широких, хотя и низких «крыльев» Гаусса, изменили статистику распределения яркости. Это приблизило величину формфактора для голограммы Гауссова пучка к соответствующей величине формфактора голограммы изображения, но одновременно уменьшило его эффективный размер в площади кадра, что привело к некоторому снижению средней дифракционной эффективности. На рис. 4в видно, что Ω снизилась с 44,9% (рис. 4б) до 28,5 % (рис. 4в). Как указывалось выше, увеличение полуширины усечённого снизу Гауссова распределения, используемого для расчётов рис. 3в и рис. 4в, усечённого снизу на 20%, привело к росту Ω до сравнимых с рис. 3а, 4а значений.
В целом приведённые результаты помогают понять предельные характеристики голограмм сложных изображений и даже объяснить некоторые эффекты, на которых прежде исследователи не заостряли внимания.
Так, известно, что яркость записанных на голограммах «вынесенных» из плоскости голограммы изображений может быть существенно выше, чем записанных в объёме, близком от поверхности голографической пластинки [9, 10]. Это можно объяснить тем, что записываемое вблизи голографической пластинки изображение имеет одно статистическое распределение яркости, а при удалении – другое. Так, на распределение яркости, а иногда и видности в плоскости регистрации голограммы оказывает влияние перераспределение амплитуды электромагнитного поля в свободном пространстве. Такое перераспределение описывается, как известно, преобразованием Кирхгофа и выглядит как некоторое «размазывание», похожее на дефокусировку амплитуды светового сигнала по полю голограммы, тем самым приближая к равномерному распределению яркости по полю. В этом случае, как было отмечено в [6], влияние формфактора ослабевает и средняя дифракционная эффективность голограммы приближается к описываемой в (2) с ψ = 1 и Ω = 1.
Заключение
На основе полученных в работе результатов можно сделать вывод о более широкой применимости вычисленных в [7] для Гауссовых пучков значений формфактора. Здесь формфактор – это константа, учитывающая весовую функцию яркости с учётом влияния нелинейности фотоотклика как самого голографического материала, так и показанной в [8] синусоидальной зависимости, определяемой самосогласованной дифракцией объектной и опорной волн.
На основе анализа более чем 30 изображений можно сделать вывод, что даже отклонения от Гауссова статистического распределения не дают существенного изменения формфактора.
Следует отметить, что методика использования формфактора годится и для других статистических распределений. Для некоторых видов голографических сигналов, как нам представляется, могут реалии- зовываться и другие статистики распределения яркостей, похожие, например, на статистики Бозе – Эйнштейна, Стьюдента, Коши или др. Но оптимальный выбор экспозиции для голографических портретов будет близок к оптимальному выбору экспозиции для Гауссовых пучков в силу близости статистики распределения яркости и, вследствие этого, близости их формфакторов к величине Ψ = 0,61.
Список литературы Формфактор голограмм сложных изображений
- Суханов, В.И. Разработки ГОИ в области объемных регистрирующих сред для голографии/В.И. Суханов, А.В. Вениаминов, А.И. Рыскин, Н.В. Никоноров//В кн.: Юрий Николаевич Денисюк -основоположник отечественной голографии: Сборник трудов Всероссийского семинара/СПб: СПбГУ ИТМО, 2007. -С. 262-276.
- Шелковников, В.В. Получение и свойства голографического фотополимерного материала в гибридной золь-гель матрице/В.В. Шелковников, В.В. Русских, Е.В. Васильев, Е.Ф. Пен, В.И. Ковалевский, И.А. Кучин//Оптический журнал. -2006. -Т. 73, № 7. -С. 65-69.
- Шойдин, С.А. Дифракционная эффективность голограмм, записанных гауссовыми пучками/С.А. Шойдин. -В кн.: Интерэкспо Гео-Сибирь-2015. СибОптика-2015: сборник материалов. -Новосибирск: СГУГиТ, 2015. -Т. 1. -С. 71-76.
- Shoydin, S.A. Requirements to lasers and formfactor of holograms/S.A. Shoydin//Optical Memory and Neural Networks (Information Optics). -2016. -Vol. 25, Issue 2. -P. 287-294. - DOI: 10.3103/S1060992X16020053
- Шойдин, С.А. О требованиях к параметрам источника излучения для голографии/С.А. Шойдин. -В кн.: Лазеры. Измерения. Информация -2013: сборник докладов. -СПб.: Изд-во СПб. Политехнич. ун-та, 2013. -Т. 1. -С. 94-107.
- Шойдин, С.А. Требования к лазерному излучению и формфактор голограмм/С.А. Шойдин//Оптический журнал. -2016. -Т. 83, № 5. -С. 65-75.
- Шойдин, С.А. Метод достижения максимальной дифракционной эффективности голограмм на основе оптимизации формфактора/С.А. Шойдин//Компьютерная оптика. -2016. -Т. 40, № 4. -С. 501-507. - DOI: 10.18287/2412-6179-2016-40-4-501-507
- Кольер, Р. Оптическая голография/Р. Кольер, К. Беркхарт, Л. Лин; пер. с. англ. -М.: Мир, 1973. -C. 291.
- Shoydin, S.A. Application of Denisuk`s hologras in advertising/S.A. Shoydin//Optical Memory and Neural Networks (Information Optics). -2013. -Vol. 22, Issue 4. -P. 272-274. - DOI: 10.3103/S1060992X13040127
- Шойдин, С.А. Парадоксальные изображения и парадоксальные технические решения в голографии на примере гражданских разработок/С.А. Шойдин//Известия Высших учебных заведений. Физика. -2015. -Т. 58, № 11-3. -С. 140-143.


