Формирование алгоритмов управляющих воздействий на основе численных методов

Изучение нелинейных динамических систем относится к одной из сложных задач современной теории автоматического управления [1], где в настоящее время интенсивно развиваются два направления - траекторное управление [2] и топологические методы [3] анализа и синтеза многомерных систем. При проектировании систем управления сложными многосвязными нелинейными динамическими объектами [4], особенно в роботизированных и мехатронных комплексах, выделяют этап построения требуемых траекторий изменения физических координат, обеспечивающих согласованное движение объекта, и этап синтеза локальных регуляторов, поддерживающих заданные состояния объектов. Траекторное управление реализуется в локальных подсистемах, где необходимо сформировать такое управляющее воздействие, при котором состояние объекта или его выход изменялись бы в соответствии с требуемой траекторией или программой. Дополнительные условия, накладываемые на устойчивость и качество процессов в замкнутых системах, относят траекторное управление к классу обратных задач динамики [5; 6].

Топологический подход [1] или методы дифференциальной геометрии [3] позволяют теоретически найти такое преобразование, при котором в новых переменных состояния многомерный нелинейный объект описывается линейными уравнениями. Главная сложность заключается в существовании и определении диффеоморфизма между исходной и линеаризованной моделями. Практические результаты получены для аффинных объектов и траекторного управления, а задача синтеза локальных регуляторов решается методами обратных задач динамики [2; 5].

Проблема по строения регуляторов нелинейными объектами остается особенно актуальной для траекторных задач. Одним из способов ее решения является прямое оптимальное управление [7], которое сводится к определению обратных функций. Решение существует только для зависимостей, обладающих свойством диффеоморфизма, поэтому в [7] предлагаются приближенные методы, основанные на линеаризации и приводящие к рекуррентным алгоритмам.

Рекуррентные соотношения широко используются в численных методах, поэтому и предлагается подход, основанный на применении в дискретном регуляторе алгоритмов в форме итерационных процедур. Исследуемый объект в локальной системе управления состоит из нелинейного элемента (НЭ) и линейной части [2; 5; 6]. В рабо- те рассматривается случай одного НЭ с целью получения более простых и удобных для сравнительного анализа аналитических выражений.

Постановка задачи. Пусть дискретный стационарный объект описывается разностным уравнением xk+1 = Axk + BФ(uk), x 0 = x (0 ) .                       (1)

Здесь x - n -мерный вектор переменных состояния; A и B - матрица и вектор с известными постоянными параметрами размерами n х n и n х 1 соответственно; и - управляющее воздействие; ф ( и ) - непрерывная функция, являющаяся характеристикой нелинейного элемента, которая принадлежит классу ф ( и ) е С* , т е. существуют ее первая, вторая и третья производные.

В системах траекторного управления для наблюдаемого вектора состояния xk+ 1 должно выполняться условие xk+1 = gk+1,                       (2)

где g - n -мерный вектор требуемого закона изменения состояния объекта (системы) или желаемая траектория движения.

В задачах обратной динамики [6; 7] подставляют равенство (2) в модель объекта (1) и по сути получают уравнение gk +1 -Axk -BФ(uk) = 0 которое можно свести к скалярному

B ⁺ ( g k +1 ^- Ax k ) ^- ф ( u k ) = ⁰           (3)

В формуле (3) под B ⁺ понимается псевдообратная матрица размером 1 х n , для которой необходимо, чтобы соблюдались условия

B ⁺ ■ B = 1 и B ■ B ⁺ ■ R = R , где R - n -мерный вектор.

Введем в рассмотрение следующую непрерывную функцию:

f ( g k +1 , xk , u k ) = B ⁺ ( g k +1 ^- Ax k ) ^- ф ( u k ) .    ⁽⁴⁾

Элементы векторов g_{k +} 1 и x_k известны, а численное значение u_k необходимо определить, поэтому f( ■ ) является функцией только одного аргумента и , и выражение (4) можно записать в виде

f ( u ) = B ⁺( g k +1 ^- Ax k ) ^- ф ( ^u ) .          (5)

Несложно убедиться, что для частных производных выполняются равенства

f ^{( i )} ( и ) = -ф ⁽ - '⁾ ( и ) , i = 1,2,...             (6)

и функция f ( и ) также принадлежит классу fи ) е С ³ .

Из сравнения выражения (5) дляДи) и уравнения (3) следует, что при нахождении управления и = ик должно выполняться равенство f (и ) = 0.                      (7)

Таким образом, определение управляющего воздействия и_к сводится к задаче нахождения корня уравнения (7). При этом будем полагать, что он существует и является вещественным и единственным. В прикладной математике используют приближенные решения на основе итерационных процедур, которые и предлагается использовать как рекуррентные алгоритмы формирования u_k .

Синтез рекуррентных алгоритмов формирования управляющих воздействий . Одним из наиболее известных численных процедур первого порядка, использующих только первую производную, является метод Ньютона [8] или Ньютона-Рафсона [9], когда формируется дискретная последовательность u_k на основе следующего правила:

U k = U k - 1 - [ fL Г¹ f k -1 .              (8)

Здесь как и в дальнейшем fk-1= f(i) (Uk-i), i = 0,1, 2,3.              (9)

Рекуррентные формулы методов второго порядка содержат как первую, так и вторую производную от функции f ( U ). В общей теории численного решения нелинейного уравнения (7), приведенной и рассмотренной в работе [8], выделяются метод Чебышева, для которого строится итерационный процесс вида 1

^uk = ^uk -1 ^-l ( ^fk -1 ) ³ I ^х

Г , х 2 ^J 1             (10)

x^ f k -1 ( f k -1 ) + 0,5 f k '-, f k ²-, ]

и алгоритм Хэлли, вычисляющий приближение u_k по формуле

• ^uk = ^uk -1 ^-

• -[(fk-1 )2 -0,5f/-1 fk-1 ]" fk-1 fk-1.

Более общие методы второго порядка, использующие линеаризацию f(и_к ), предлагаются в [10], и рекуррентные процедуры на их основе имеют вид

Uk = Uk-.-[fk'-.]-1 [fk-. + 0,5fk"-, 5k] ;(12)

Uk = Uk -.-[ fk-. + 0,5 fk"-, 5 k ]-1 fk -..(13)

В выражения (12) и (13) входит величина d _k , которую рекомендуется определять следующим образом:

• ⁵ k = v k - ^Uk - 1 ^.

Здесь v_k - это k -е приближение к решению уравнения (7), вычисленное с помощью любого итерационного метода.

Применение процедуры первого порядка (например, Ньютона-Рафсона) к определению v_k позволяет записать, что

V k = U k _, - [ f k '-, Г¹ f k -1 ;               (14)

5 k =- [ f k -1 ' f k -1 .                (15)

Подстановка d _k в форме (15) в выражение (12) приводит к рекуррентной процедуре (10), т. е. к методу Чебышева. Аналогично можно показать, что алгоритм Хэлли (11) является частным случаем итерационного процесса вида (13).

Конкретные алгоритмы определения управляющих воздействий U_k в рекуррентных формах получаются, если в выражения (8), (10) и (11) подставить формулу (5) для функции fи ) и учитывать соотношение (6) для ее частных производных. Алгоритмы второго порядка, построенные на основе методов Чебышева и Хэлли, целесообразно реализовать в виде двухступенчатой процедуры. Первоначально, используя метод Ньютона-Рафсона, вычисляется значение v_k по формуле (8), затем - 5 _k , а на второй ступени управляющее воздействие u_k уточняется в соответствии с выражениями (12) или (13).

Свойства итерационных процедур в прикладной математике [9] оценивают по степени приближения дискретной последовательности u_k к точному решению и* нелинейного уравнения (7) и для этого получают и исследуют аналитические зависимости s _k = u_k - и * от s _k - , = u_k -1 - и *. Например, по показателю скорости сходимости метод Ньютона-Рафсона имеет квадратичную, а алгоритмы Чебышева и Хэлли - кубическую сходимость [8; 9]. Анализ малых отклонений s _k - ] ^ 0 позволяет также говорить и о более высокой точности методов второго порядка в определении и *, так как для них s _k пропорциональна s k - 1 , в то время как у Ньютона-Рафсона - s 2 - 1 . При реализации рекуррентных процедур формирования u_k в замкнутых системах управления точность оценивается по степени близости выходной переменной к входному или задающему воздействию [1; 2; 5].

Анализ точности процессов управления в замкнутых системах. Динамическая ошибка в замкнутой системе ek +1 представляет собой n-мерный вектор и вычисляется по формуле ek +1 = gk +1 - xk +1.                  (16)

Дискретное значение xk +1 является реакцией объекта на управляющее воздействие uk. Допустим, что uk формируется на основе выражения (8) метода Ньютона-Рафсона, тогда при условии, что 5k ^ 0, модель (1) записывается в виде xk + J = Axk +

+ B [ф k -1 +Q k -. 5 k + 0,5 Q k -1 5 2 + O ( 5 ³ ) ] .    ⁽¹⁷⁾

Здесь и в дальнейшем приняты обозначения

Q ki -1 Q' ( U k -1 ) , i = 0, 1, 2, 3.

Разность управлений 5 _k определяется по формуле (15) и с учетом выражений (5) и (6) вычисляется следующим образом:

• ⁵ k =^[Q k -1 ] ^{1 [} B ⁺( g k +1 - Ax k ) ^-Ф k -1 ] .      ⁽1⁸⁾

После подстановки 5k в уравнение (17) и несложных преобразований получается xk+1 = gk+1+ 0,5 B Qk-15 k+ O (5k).

Динамическая ошибка (16) при реализации в системе алгоритма управления (8) на основе метода первого порядка Ньютона-Рафсона определяется выражением ek'+1 =-0,5 B ф^. 52 + O (5k)          (19)

или приближенным равенством ek1+1 ^ 0,5 B Qk-1 5 k,                  (20)

которое получено из формулы (19) при 5 _k ^ 0 .

Допустим, что в системе реализуются алгоритмы управления второго порядка. Введем для разности управлений обозначение

xk +1 = g k +1 ⁺

A u_k = u_k ^- u_k -1 .

+ B

По аналогии с записью (17) представим уравнение объекта (1) при A u_k ^ 0 в форме

0,5 ф k A u k - 0,5 ф k - 1 5 2 + + 0,25( ф k _        k -1 )² 5 k +

⁺ 6 Ф™ 1 ^A u k ⁺ O ( ^{A u 4})

+ B

x k +1 = Ax k ⁺

^ф k - 1 ^+ф к -1 ^A u k ⁺ 0,5 ф " - i ^A u k ⁺

+ ' ф k ³-1 ^A u k + о ( ^A u 4 )

Оценим точность системы при формировании управления u_k в соответствии с выражением (12) метода Чебышева. Разность управлений A u_k записывается в виде

Представим выражения A u_k ² и A u_k ³ , используя для

A u_k формулу (28), в следующем виде:

A u ( = 5 k -[ф k _ 1 ] ^- 1 Ф k -1 5 k + O ( 5 4 ) ;

A uk =5k + O (5 k), тогда состояние объекта xk + 1 записывается в форме

^A u k =[ф k -1 ] 1 ^{x x[ B +} ( g k +1 ^- Ax k ) ^-Ф k -1 ^{- 0,5} Ф к- 1 5 k ] ,

где 5 _k определяется выражением (18).

Формула (22) с учетом равенства (18) переписывается как

A u_k = 5_k- 0,5 ф²      ' Ф‘- ,§ 2 .          (23)

k        k                  k 1           k 1 k

+ B

1 ф(3-1

-

x k +1 = g k +1 ⁺

0,25 ( ф ( _ 1 )^{- 1}( ф к -1 )² 15 k + O ( 5 ( ) . ⁽³⁰⁾

По аналогии с выражением (25) вводится

P 21 = 6 ф к - 0,25 ( ф к -1 )^{- 1}( ф к -1 )²        (31)

и для вектора динамической ошибки при 5 _к ^ 0 справедливо приближенное равенство

■    -- B Р 21 5 k .                 (32)

После подстановки в уравнение (21) только A u_k , определяемого выражением (22), получается, что

+ B

xk +1 = g k +1 ⁺

0,5 Ф k -1 A u 2 - 0,5 Ф k -1 5 k +

^{+ 1} ф k ^з-1 ^a u k + о ( ^a u k )

Представим A u_k ² и A u_k ³ в виде

Auk2 = 5k -[фk -1 ]-1 Фк-1 5k + O (54), a uk=5k+о (5 k), тогда

+ B

xk +1 = g k +1 ⁺

6 ф k ³-1 - 0,5 ( ф k -1       Ф 1 )² 5 k + O ( 5 4 ) .

Введем обозначение

P 22 = ¹ Ф k ³-1 - 0,5 ( ф k -1 )^{- 1}( Ф k -1 )².          (25)

Точность системы при использовании в устройстве управления алгоритма Чебышева (при 5к ^ 0 ) оценивается приближенным равенством ek+21 -- B в- 5k.                 (26)

Допустим, что в системе реализуется алгоритм Хэлли, тогда

A uk =[Фk -1+ 0,5 ф(- 15 к ]1 x x[ B +(gk +1 - Axk )-Ф k -1 ], где 5k также определяется формулой (18).

Выражение (27) при 5 _к ^ 0 представляется рядом Тейлора вида

A u =5 k - 0,5 ^[ф k -171 ф ( _ 1 5 k + + 0,25 [ ( ф k _ 1 ) 2 ] ^-( ф к -1 ) 2 5 k + O ( 5 4 ) .

После подстановки в уравнение объекта (21) разности A u_k в форме (27) получается

Сравнительный анализ методов второго порядка предлагается осуществлять следующим образом. Допустим, что в системе реализован идеальный алгоритм управления второго порядка с использованием 5k2 (примеры таких итерационных методов приводятся в [9]), тогда ошибка такой квадратичной аппроксимации определяется приближенным равенством ek2_+1 »-1B ф^_1 5(.                 (33)

Введем для оценки степени близости приближенных алгоритмов к идеальной системе второго порядка разности

(21)       (2)        (21)           (22)       (2)        (22)

^{A e}k + 1 ^ek + 1 ^ek + 1 ^{и A e}k + 1 ^ek + 1 ^ek + 1 ^.

Определим величину 5 k из выражения (32) и подставим в формулы (31) и (26). После несложных преобразований получается

^A e ( ’+1 = ^{1,5 [}ф к -1 Ф ? -1 ] ¹ ( ф к -1 ) 2 « ( ’+1 ,        (34)

Ae к ”) - 3 [Ф к ^         ф к -1) ² « к ':.         (35)

Анализ выражений для дискретных значений приближенных ошибок (20), (26) и (32) при 5 _к ^ 0 говорит о более высокой точности систем, в которых реализованы алгоритмы второго порядка. В методе Ньютона–Рафсо-на, в соответствии с формулой (20), динамическая ошибка е ( ’+ 1 пропорциональна 5 ( , а в методах второго порядка, согласно выражениям (26) и (32), ошибки e k² и е^ зависят от 5 ( , т е. на порядок меньше. Аналогичный вывод получен и для итерационных процедур нахождения корня нелинейного уравнения [9; 10].

Формулы для оценки норм векторов приведем в силу их компактности только для соотношений (34) и (35). Допустим, что m1 = min|ф'(u)|, m3 = min|ф(3) (u)| и M2 = max |ф"(u)|, тогда                                        2

IA е '-"II ^ 1,5 м ¹1 е ™|| и |А е '”11^ 3 M rl « '”l|.

m ₁ m ₃                    m ₁ m ₃

Полученные неравенства позволяют утверждать, что при реализации в устройстве управления алгоритма Хэлли ошибка в замкнутой системе приблизительно в 2 раза меньше, чем у аналогичной системы, использующей метод Чебышева.

Пример. Рассмотрим объект управления первого порядка, описываемый разностным уравнением xk+1 = axk + bthuk, x0 = 0.          (36)

Выбраны следующие значения параметров: a = 0,6 и b = 0,9. Требуемая траектория движения – единичная функция, т. е. g_{k + 1} = 1.

Характеристика НЭ ф(u) = th u принадлежит классу ф(u) О Сц и для нее выполняется свойство диффеоморфизма [2], поэтому существует аналитическое решение, и управляющее воздействие определяется по формуле uk = arcth [b"* (gk +1 - axk)], u0 = 0 .

В замкнутой системе переход из нулевого состояния x ₀ = 0 в конечное x ₁ = 1 будет происходить за один шаг.

Рассмотрим применение приближенных алгоритмов. Построим в соответствии с формулой (5) функцию f ( u ) для исследуемого объекта в виде

f ( u ) = b -1 ( g k +1 ^- ax k ) ^{- th} u .           ⁽³⁷⁾

Допустим, что управляющее воздействие uk будем формировать на основе итерационного метода Ньюто-на–Рафсона, поэтому, используя выражение (8), получим uk = uk-1 + b-1 ch2uk-1 [gk +1 -axk -bthuk-1], u 0 = 0.                     (38)

Алгоритмы второго порядка могут быть получены непосредственно из формул (10) и (11) либо из процедур (12) и (13), в которых для исследуемого объекта величина 5 _k равна

5 k = b ^{- 1} ch² u k -1 ^[ g k +1 ^- ax k ^- b th u k -1 ] .

Графики переходных процессов в замкнутых системах, в которых реализованы рассматриваемые приближенные алгоритмы формирования управляющих воздействий, приведены на рисунке. Переход системы из нуле- вого состояния в конечное при использовании алгоритмов второго порядка происходит на один шаг быстрее.

Экспериментальные исследования для проверки адекватности полученных аналитических выражений проводились следующим образом. Затухание переходных процессов во всех системах происходит до пятого шага, поэтому при k = 5 происходит кратковременное возмущение состояния объекта на величину A x . В системах в соответствии с алгоритмами (8), (12) или (13) вырабатывается управляющее воздействие u_k , которое компенсирует появившееся отклонение A x практически за два шага (см. рисунок). Теоретические значения ошибок рассчитывались для метода Ньютона–Рафсона по формуле (20), а алгоритмов Чебышева и Хэлли – соответственно по выражениям (26) и (31), в которых использовались 5 _k , полученные в результате моделирования. Экспериментальные ошибки вычислялись непосредственно по формуле (16).

Результаты моделирования при A x = 0,1 всех трех систем в виде теоретических и экспериментальных значений ошибок приведены в табл. 1.

Сравнительный анализ приведенной информации подтверждает, во-первых, адекватность полученных аналитических выражений, во-вторых, тот факт, что точность систем, в которых реализованы алгоритмы второго порядка выше, и, в-третьих, что меньшую ошибку имеет система с алгоритмом Хэлли (приблизительно в 2 раза).

Моделирование проводилось и для других значений отклонений состояния объекта и при A x = 0,7 (см. табл. 2).

Произошло ухудшение показателя точности во всех системах и возросло расхождение между экспериментальными и теоретическими значениями, так как ошибки зависят от 5 _k и необходимо, чтобы 5 _k ^ 0, а при больших A x это условие не выполняется.

Возмущение A x практически компенсируется по-прежнему за два шага. Целесообразно в регуляторах применять двухступенчатые приближенные алгоритмы, особенно на первых шагах формирования воздействия u_k . Вначале вычисляются значения v_k методом первого порядка, затем, если ошибка δ _k достаточно большая, то уточняется значение u_k предлагаемыми алгоритмами управления.

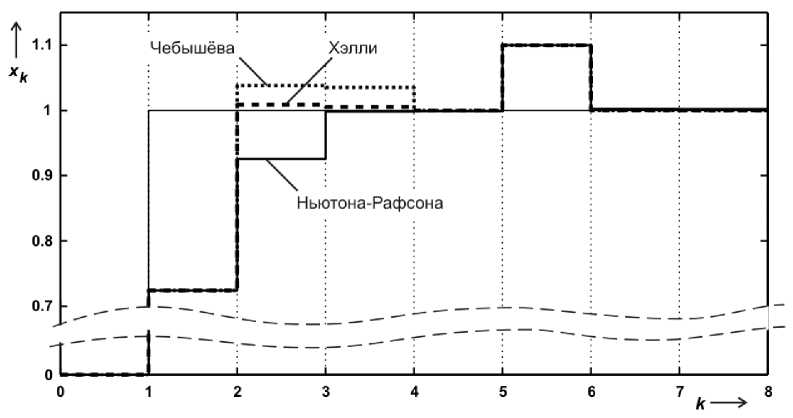
Переходные процессы в системах при различных методах управления

Таким образом, в работе была рассмотрена задача траекторного управления дискретным многомерным объектом с одним нелинейным элементом. Введена новая нелинейная функция, которая при заданных значениях требуемой траектории и наблюдаемого вектора состояния зависит только от одного аргумента – управления. Рекуррентными алгоритмами являются итерационные процедуры нахождения корня нелинейного уравнения.

Методика формирования и исследования приближенных алгоритмов приведена на примере трех, построенных на основе численных методов Ньютона–Рафсона, Чебышева и Хэлли. При реализации их в замкнутых системах получены аналитические выражения для точности процессов управления, которые предлагается использовать для сравнительного анализа. Моделирование систем и результаты экспериментальных исследований подтвердили адекватность полученных теоретических оценок точности.

Из вышеуказанного можно сделать вывод о возможности применения для формирования рекуррентных алгоритмов управления достаточно хорошо известных и изученных итерационных процедур решения нелинейных уравнений.