Формирование близкорасположенных световых пятен на основе лазерных зеркальных пучков Эйри

Формирование определённых распределений интенсивности, состоящих из близкорасположенных световых пятен, представляет практический интерес для задач взаимодействия фемтосекундного лазерного излучения с веществом [1–5].

В частности, в работе [3] было показано, что под действием лазерного предымпульса на поверхность жидкой галлиевой мишени происходит формирование микроструй вещества. На основе проведенных экспериментов и результатов численного моделирования формирования микроструй авторами работы [4] было показано, что выброс струи с поверхности жидкой мишени происходит в результате пересечения фронтов ударных волн, распространяющихся под поверхностью мишени от различных горячих пятен в распределении плотности энергии в пятне фокусировки.

Таким образом, создание неоднородного регулярного поперечного распределения плотности энергии лазерного пучка, состоящего из близкорасположенных горячих пятен, представляет большой практический интерес для задач взаимодействия фемтосекундного лазерного излучения с веществом. Для этой цели удобно использовать модовые пучки, сохраняющие свою конфигурацию (с точностью до масштаба) на неограниченном расстоянии, а также при прохождении через линзовые системы.

Универсальным методом генерации поперечных лазерных мод является модуляция фазы исходного Гауссова пучка. Для этого может использоваться про- странственный модулятор света [6–8] или дифракционные оптические элементы (ДОЭ) [9–11].

Ранее, в работе [12], мы сравнивали формирование в фокальной плоскости близкорасположенных световых пятен с помощью дифракционной решётки и ДОЭ, согласованных с модами Эрмита–Гаусса (ЭГ). Было показано, что при формировании набора близкорасположенных световых пятен период дифракционной решётки становится очень малым и фаза фактически соответствует модам ЭГ. Однако в последнем случае световые пятна имеют не только различный размер, но и различную интенсивность.

В работе [13] авторами исследовалось влияние частичного кодирования ДОЭ на качество формирования модовых распределений ЭГ при освещении оптического элемента фемтосекундным излучением. Было показано, что хорошее качество формирования световых пятен и относительная устойчивость к хроматической дисперсии при использовании импульсного лазерного излучения обеспечивается при низких индексах мод. Для высших мод требуется дополнительное кодирование фазовой функции, что приводит к снижению дифракционной эффективности [14, 15].

Таким образом, хотя пучки ЭГ и обладают модовыми свойствами, т.е. сохраняют свою структуру при распространении в свободном пространстве и прохождении через линзовые системы [16], формируемые при этом распределения имеют определённые недостатки.

Компенсировать неравномерность интенсивности при сохранении модовых свойств можно при исполь- зовании вместо мод ЭГ симметризованных или зеркальных пучков Эйри [17]. В отличие от пучков Эйри–Гаусса [18] или экспоненциальных пучков Эйри [19], зеркальные пучки Эйри представляют собой симметризованную суперпозицию отсечённых по нулевому значению функций Эйри и напоминают своей структурой моды ЭГ. Пространственный спектр зеркальных пуков Эйри состоит из довольно равномерных по интенсивности максимумов [17].

В данной работе выполняется сравнительное исследование формирования близкорасположенных световых точек с помощью мод ЭГ и зеркальных пучков Эйри. Кроме того, рассмотрено формирование близкорасположенных световых пятен на основе решёток с комплексно сопряжёнными дифракционными порядками. Формирование картин сравнивается как по соблюдению условия равенства размеров и интенсивности световых пятен, так и по устойчивости к дефокусировке.

Экспериментальное исследование изготовленных образцов ДОЭ с использованием перестраиваемого лазера позволило выяснить устойчивость сформированных мод ЭГ и зеркальных пучков Эйри к хроматической дисперсии.

1.    Моделирование

Рассмотрим формирование близкорасположенных световых пятен в фокальной плоскости линзы на основе решеток с комплексно сопряжёнными дифракционными порядками, а также с помощью мод ЭГ и зеркальных пучков Эйри.

Для моделирования воспользуемся преобразованием Фурье:

∞

G ( u ) = J g ( x )exp

-∞

2 π

- i   xu

λ f

d x ,

где f – фокусное расстояние линзы, λ – длина волны излучения.

Для преобразования (1) известно свойство смещения:

∞

G ( u - a ) = J g s ( x ) exp

-∞

2 π

- i   xu

λ f

d x ,               (2)

I . 2na где gs(x) = g(x)exPH     x

I ^f

Свойство (2) позволяет формировать произвольный набор смещённых копий исходного объекта. Если в объектной плоскости установить оптический элемент с комплексной функцией вида:

t ( x ) = ^ с p exp I i p \

2 πα p x

λ f

,

то в фокальной плоскости в точках α p , соответствующих пространственным несущим частотам, будут формироваться копии объекта с интенсивностью, пропорциональной | c p |².

Этот способ размножения световых распределений в заданной конфигурации используется для оп- тического захвата и манипулирования частицами [20, 21], для оптического разложения светового поля по некоторому базису [22, 23], а также для разделения лазерного пучка [24, 25].

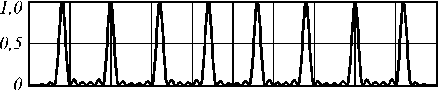
На рис. 1 показаны результаты фокусировки ( f =250 мм) плоского лазерного пучка радиусом 10 мм с базовой длиной волны 800 нм, прошедшего бинарную дифракционную решётку, формирующую восемь световых пятен с коэффициентами c p в (3), имеющими одинаковую амплитуду, но противоположную фазу у соседних слагаемых. В этом случае формируемые решёткой дифракционные порядки, расположенные даже очень близко друг к другу, не будут сливаться в отличие от случая, рассмотренного в [12].

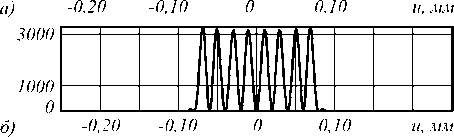
Как видно из рис. 1, уменьшать расстояние между световыми пятнами за счёт уменьшения размера несущей пространственной частоты α p можно лишь до определённого предела. В частности, до момента, когда расстояние между световыми пятнами становится равным размеру самих пятен (рис. 1 б ). В этом случае ширина световых пятен равна ∆ = 0,02 мм.

Дальнейшее уменьшение α p приводит не только к сближению световых точек с одновременным их сужением ∆ = 0,01 мм, но и к перераспределению энергии между ними нежелательным образом (рис. 1 в ).

в)

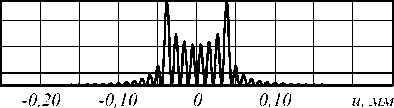
Рис. 1. Формирование 8 световых пятен с помощью дифракционной решётки – нормированное распределение в фокальной плоскости для различных значений параметра α p : 0,93 мм (а), 0,31 мм (б), 0,16 мм (в)

Расстояние между дифракционными порядками однозначно определяется из соотношения для дифракционной решётки:

d sin θ _m = m λ ,                                   (4)

где d – размер периода решётки, m – номер дифракционного порядка.

В частности, первый порядок дифракции соответствует отношению длины волны излучения к размеру периода решётки:

sin θ ₁ = λ d .                                        (5)

Чтобы приблизить дифракционные порядки друг к другу, нужно сделать угол дифракции как можно меньше, т.е. максимально увеличить размер периода решётки.

Очевидно, что минимальное расстояние не может быть меньше дифракционного предела:

Б=^

2 R

где R – радиус оптического элемента.

В соответствии с формулой (6) дифракционный предел для иллюстрируемого на рис. 1 случая равен 5 = 0,01 мм. Однако наилучшая ситуация по равномерности интенсивности и близости световых пятен наблюдается для А = 0,02 мм (рис. 1 б) .

Попытка сблизить дифракционные порядки приведёт к увеличению периода до размера оптического элемента, что фактически означает вырождение решётки, т.к. в этом случае она будет работать в нулевом порядке дифракции. Данный факт детально обсуждался в работе [12]. Поэтому было предложено использовать для формирования близкорасположенных световых точек бинарные ДОЭ, согласованные с модами ЭГ [26].

Однако распределение световых пятен у мод ЭГ не очень равномерное – крайние пятна крупнее и интенсивность в них выше. Поэтому в данной работе мы рассматриваем ещё один тип пучков, обладающих модовыми свойствами – симметризованные или зеркальные пучки Эйри [17].

Моды ЭГ во входной плоскости имеют следующий вид:

( х1 ^

Т n (% ) = exp I — —I Hn       ,(7)

( о JI о I

Из вышеприведённого выражения видно, что интенсивность функции (9) не меняется при различных значениях z , а лишь смещается пропорционально квадрату этого параметра.

Однако, так как функция Эйри является бесконечной, то реализовать её проблематично. Поэтому обычно во входной плоскости ( z = 0) рассматривают ограниченную по энергии функцию [18, 19]:

V ( х ,0) = Ai( х )exp( ax ), (10)

или

( _х 2

V ( х ,0) = Ai ( х ) exp I---

I o ²

.

Заметим, однако, что аподизация функции Эйри экспоненциальной или Гауссовой функцией приводит к быстрой потере модовых свойств такого пучка при распространении. Поэтому в работе [17] было предложено формировать функции Эйри, ограниченные апертурной функцией:

( х + ( х „ + c ,) /2 ) V _n ( х ) = Ai( х ) • rect ---------------- ,

I     ^c 0 ^{— х}п    J

где c 0 – граница справа в соответствии с затуханием функции в положительной части аргумента, x n – граница слева, соответствующая n -му корню.

Известно, что для действительных x :

1 7

^{A,< х} ) = 2 П I exp i

^

— 7

t ³

—+ xt

d t .

где о - радиус перетяжки Гауссова пучка, H n ( х ) - полином Эрмита.

Распространение мод ЭГ в параксиальной области свободного пространства описывается следующей формулой:

Рассмотрим сумму функции Эйри с её зеркальным отражением. С учётом (13) и масштабирующего коэффициента получим:

1 7

Ai( х ) + Ai( — х ) = — f cos ( a t ³) exp ( ixt ) d t ,       (14)

n

—7

V

n

х exp

exp

(    ikx ² )

H„

| 2 R ( z ) J ^K

( % )

I o ( z ) ^J ’

где n ( z ) = arctg( z / z 0 ), R ( z ) = z (1 + z 2 / z 2 ), z 0 = k o ²/2, о ( z ) = о ^1 + z ²/ z 2 , k = 2 п/% - волновое число.

Из выражения (8) видно, что моды ЭГ распространяются в свободном пространстве без изменения структуры, лишь масштабно увеличиваясь.

Функции Эйри как решение параксиального волнового уравнения распространения в свободном пространстве имеет следующий вид:

т.е. в пространственной спектральной (фокальной) плоскости получаем набор световых точек, в соответствии с cos ( a t ³), которые являются близкорасположенными и имеют одинаковую интенсивность.

Аналогичный результат можно получить для суммы смещённых в разные стороны функций Эйри. Таким образом, зеркальные пучки Эйри можно формировать в виде суммы смещённых ограниченных распределений (12):

V n = Ai n ( х — х п ) + ( — 1) ^{n — 1}Ai n ( — х — х п ) .          (15)

V ( х , z ) = Ai

х —

z

2 k

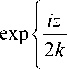
x

z

3 I 2 k

Введение коэффициента в (15) связано с соблюдением гладкости сшивки двух функций в точке зеркального отражения (в данном случае при x =0).

На рис. 2 показаны результаты сравнительного моделирования формирования набора из 8 световых пятен с использованием мод ЭГ и зеркальных пучков Эйри.

Как видно, пучок Эйри обеспечивает более равномерное распределение интенсивности световых точек, чем моды ЭГ, хотя крайние световые пятна остаются более широкими, чем остальные.

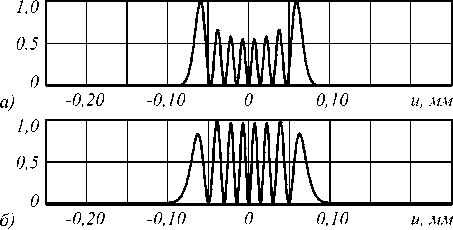
Рис. 2. Формирование набора световых пятен в фокальной плоскости с использованием мод ЭГ (а) и зеркальных пучков Эйри (б)

Это общий недостаток модовых распределений по сравнению с распределением, обеспечиваемым решётками с комплексно сопряженными дифракционными порядками (рис. 1). Хотя нужно отметить, что распределения интенсивности на рис. 1 в и 2 а похожи.

Тем не менее, модовые пучки обладают другим преимуществом, не свойственным полям, созданным решётками, а именно, сохранение своей структуры при распространении в свободном пространстве и прохождении через линзовые системы, включая устойчивость к дефокусировке.

На рис. 3 показано моделирование распространения рассмотренных распределений вблизи фокальной плоскости.

Как видно, распределения, формируемые решётками, очень быстро теряют свою структуру при смещении поля из фокальной плоскости (рис. 3 а , б ). Причём чем меньше размер световых пятен, тем быстрее они рассеиваются. Модовые распределения (рис. 3 в , г ) сохраняют свою структуру, меняется только масштаб.

Таким образом, рассмотренные способы формирования близкорасположенных световых пятен обладают различными преимуществами и недостатками. Выбрать более подходящий способ можно в зависимости от особенностей решаемой задачи.

• 2.    Экспериментальное исследование влияния хроматической дисперсии на фокальную картину при использовании ДОЭ

Одна из трудностей, возникающих при использовании средств дифракционной оптики для формирования заданного распределения плотности энергии в пучке фемтосекундного излучения, связана с широким спектром фемтосекундного импульса (вплоть до 200 нм FWHM) [27]. Микрорельеф ДОЭ является оптимальным для монохроматического излучения, поэтому на качество формируемого распределения интенсивности в этом случае большое влияние оказывает хроматическая дисперсия [12]. Поэтому в данном разделе исследуется влияние хроматической дисперсии на фокальную картину при использовании рассмотренных ДОЭ.

Технологически создавать заданное амплитуднофазовое распределение сложно, но полное игнорирование амплитудной информации может приводить к очень существенному искажению фокальной картины (рис. 4).

Причём в зависимости от размера освещающего пучка

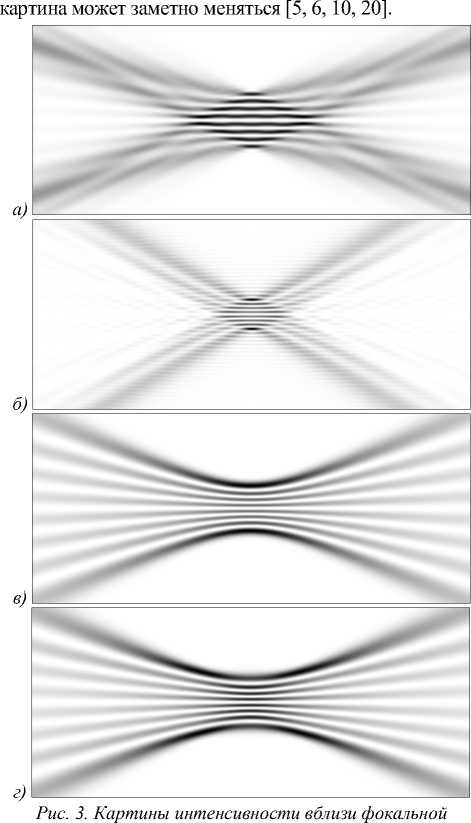
плоскости z е [ 240 мм, 260 мм ], и е [- 0,25 мм, 0,25 мм ] для решёток с a p = 0,31 мм (а), a p = 0,16 мм (б); моды ЭГ (в) и зеркального пучка Эйри (г) (негативные изображения)

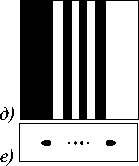
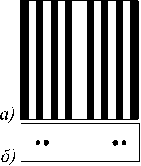
Рис. 4. Формирование набора световых пятен (нижний ряд) при освещении Гауссовым пучком некодированных фазовых ДОЭ (верхний ряд): для решётки (а),(б), мод ЭГ (в),(г) и зеркальных пучков Эйри (д),(е)

Для снижения погрешности формирования заданного распределения и снижения зависимости от размера пучка применяют частичное кодирование амплитудной информации в фазовую [9, 20]. Результаты оптимизации кодирования показаны на рис. 5.

Экспериментальное исследование изготовленных образцов ДОЭ, формирующих моды ЭГ и зеркальные пучки Эйри, производилось с помощью перестраиваемого по длине волны лазера EKSPLA NT200 Series.

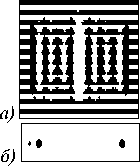
Рис. 5. Формирование набора световых пятен (нижний ряд) при освещении Гауссовым пучком кодированных фазовых ДОЭ (верхний ряд): для решётки (а), (б), мод ЭГ (в), (г) и зеркальных пучков Эйри (д), (е)

Длина волны перестраивалась в диапазоне от 840 нм до 1000 нм с шагом 20 нм. Экспериментальная схема показана на рис. 6. С помощью системы, образованной пинхолом PH (размер апертуры 40 мкм) и микрообъективом MO (20×, NA=0,4), осуществлялась процедура пространственной фильтрации исходного лазерного пучка перестраиваемого лазера Laser . Затем расходящийся лазерный пучок направлялся на исследуемый дифракционный оптический элемент DOE . Лазерный пучок, падающий на ДОЭ, совпадал по диаметру с диаметром ДОЭ (20 мм). Преобразованный с помощью ДОЭ лазерный пучок фокусировался с помощью линзы L (f = 250 мм ) на матрице видеокамеры CCD .

L DOE            PH MO Laser

Рис. 6. Экспериментальная схема:

Laser – перестраиваемый лазер EKSPLA NT200 Series, MO – микрообъектив (20×, NA = 0,4), PH – пинхол, DOE – исследуемый дифракционный оптический элемент, L – линза, M – зеркало, CCD – видеокамера

В экспериментах был использованы ДОЭ с глубиной травлениях 870 нм. Элементы были изготовлены методом фотолитографии (разрешение записи шаблона 10 мкм).

Экспериментально сформированные распределе- ния интенсивности при использовании перестраиваемого лазера для мод ЭГ показаны на рис. 7, а для зеркальных пучков Эйри – на рис. 8. Видно, что зеркальные пучки Эйри обеспечивают более равномерное распределение интенсивности в световых точках.

а)

г)

ж)

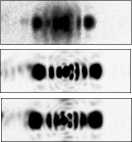
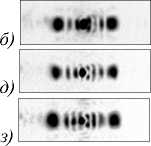
Рис. 7. Влияние хроматической дисперсии на ДОЭ, согласованный с модой ЭГ (7,0): распределения интенсивности при различных длинах волн освещающего излучения (от 840 нм (а) до 1000 нм (и) с шагом 20 нм).

Негативные изображения, размер изображений - 3 x 3 мм

Из представленных изображений видно, что распределения интенсивности для мод ЭГ наилучшего качества формируются в диапазоне 920–1000 нм, для зеркальных пучков Эйри этот диапазон несколько шире – от 880 до 1000 нм.

а)

г)

ж)

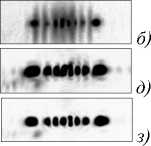
Рис. 8. Влияние хроматической дисперсии на ДОЭ, согласованный с зеркальным пучком Эйри: распределения интенсивности при различных длинах волн освещающего излучения (от 840 нм (а) до 1000 нм (и) с шагом 20 нм).

Негативные изображения, размер изображений - 3 x 3 мм

Таким образом, можно сказать, что изготовленные ДОЭ обладают спектральной устойчивостью. При отклонении длины волны от оптимального диапазона происходит только уменьшение эффективности формирования пятен, вызванное тем, что не вся энергия исходного пучка преобразуется в энергию, идущую в эти порядки. Данная часть излучения не подвергается модуляции при прохождении ДОЭ и направляется в нулевой порядок. При этом стоит отметить, что из-за дисперсии при изменении длины волны происходит смещение положения фокальной точки вдоль оси распространения пучка. При съёмке экспериментальных распределений интенсивности видеокамеру не перемещали. Такая устойчивость к дефокусировке обеспечивается модовым характером сформированных распределений.

Заключение

Выполнено сравнительное численное исследование формирования в фокальной плоскости близкорасположенных световых пятен с помощью дифракционных решёток с комплексно сопряжёнными порядками и бинарных оптических элементов, согласованных с модами Эрмита–Гаусса и зеркальными пучками Эйри.

Показано, что решётки позволяют формировать набор равномерных световых точек с высокой точностью, но формируемая картина быстро портится при смещении из плоскости фокуса. Пучки Эрмита– Гаусса в соответствии со своими модовыми свойствами обладают высокой устойчивостью к дефокусировке, но распределение интенсивности и размер световых точек в этом случае неравномерные. Зеркальные пучки Эйри представляют собой компромиссный вариант – они имеют более равномерную интенсивность световых пятен, чем моды Эрмита– Гаусса, и в то же время устойчивы к дефокусировке.

Эксперименты с перестраиваемым лазером подтвердили упомянутые преимущества зеркальных пучков Эйри по сравнению с модами Эрмита–Гаусса, а также показали хорошую спектральную устойчивость изготовленных дифракционных оптических элементов.

Работа выполнена при финансовой поддержке Российского научного фонда (РНФ), грант №16-42-01060.