Формирование и обработка изображений электронной микроскопии

Существует два основных варианта электронных микроскопов. Это просвечивающий электронный микроскоп (ПЭМ) и сканирующий электронный микроскоп (СЭМ) [1].

Механизмы формирования изображения в СЭМ отличаются от формирования изображения в оптическом или просвечивающем электронных микроскопах [2]. В оптическом и просвечивающем ЭМ изображение формируется при помощи линз и носит, таким образом, дифракционный характер. Изображение в СЭМ - это результат отображения изменений от точки к точке в характере взаимодействия электронов зонда с поверхностью мишени. Если в точке А 1 вторичный сигнал имеет величину S 1 , а в соседней точке А ₂ - соответственно S ₂, то говорят, что существует контрастность между этими точками, характеризуемая коэффициентом контраста

51 — 52 - ^ .

5 1 + 5 2    5

Контраст между двумя точками на изображении может различаться вследствие различия во взаимодействии электронов зонда с материалом мишени.

Контраст, определяемый атомным составом мишени. Коэффициент отражения электронов зависит от атомного номера и растёт с ростом последнего. Поэтому области, содержащие элементы с высоким атомным номером, будут иметь отличный от нуля контраст по сравнению с более лёгкими элементами. Таким образом, можно проводить качественный анализ атомного состава поверхности, используя полированные и даже нетравлёные образцы. Следует подчеркнуть, что коэффициент истинно вторичной эмиссии слабо зависит от атомного номера и, следовательно, во вторичных электронах такой контраст наблюдаться не будет.

Топографический контраст. Этот тип контраста возникает за счёт влияния рельефа поверхности на отражённые и вторичные электроны и имеет большое сходство с изображением, формируемым в световом микроскопе, поэтому интерпретация его во многом аналогична. Коэффициент вторичной эмиссии существенно зависит от ориентации образца по отношению к падающему пучку, причём с ростом угла падения растёт и коэффициент вторичной эмиссии. С другой стороны, в рассеянии электронов присутствует ориентационный эффект - наибольшее число отражённых электронов лежит в плоскости падения и направлено в сторону движения первичных электронов (угол падения приблизительно равен углу отражения).

Контраст каналирования электронов. Электроны при определённых углах падения могут захватываться каналами, которые образуются системами кристаллографических плоскостей. Из теории дифракции известно, что для электронов, падающих на кристалл под точным Брегговским углом для данной системы плоскостей, происходит резкое увеличение глубины проникновения электронов в материал мишени (эффект Бормана). Поэтому в этой точке поверхности кристалла происходит резкое уменьшение выхода электронов, что соответствует уменьшению её контраста на изображении. Когда это условие удовлетворяется для нескольких семейств плоскостей, на экране монитора формируется изображение пересекающихся полос, каждая из которых связана со своим определённым семейством кристаллографических плоскостей. Это используется для определения пространственной ориентировки кристалла или отдельных его участков.

Магнитный контраст. Так как на траектории движения электронов влияют магнитные поля, имеющиеся в образце или вблизи его поверхности, растровая микроскопия позволяет исследовать распределение магнитных полей на поверхности магнитных материалов.

Потенциальный (вольтовый) контраст . Аналогичные эффекты должны возникать и под действием неоднородностей электростатических полей на поверхности образца. Этот тип контраста особенно эффективно используется для наблюдения интегральных схем разной степени сложности в процессе их работы и позволяет наблюдать за изменениями потенциального рельефа, происходящими при разнообразных переключениях в схеме.

Когда первичные электроны с высокой энергией (обычно 1-30 кэВ в СЭМ) взаимодействуют с материей, происходят различные процессы, приводящие к выбросу электронов и фотонов, которые могут быть собраны, зарегистрированы и оценены [3,4]. Схема происходящих процессов иллюстрирована на рис. 1. Размер и форма возбуждённого объёма зависят от энергии электрона и материала образца.

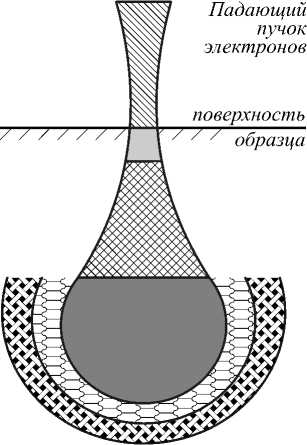
падающий электронный пучок

генерация вторичных электронов

обратно отражённые элетроны

характеристическое рентгеновское излучение

тормозное излучение

флюоресценция

Рис. 1. Схематичное изображение рассеяния падающего пучка

Когда электроны взаимодействуют с материалом, они подвергаются ряду различных упругих и неупругих столкновений [5]. Если электроны рассеяны ядрами, они не теряют энергии (упругие соударения), но рассеиваются под большими углами. Через неупругие столкновения энергия передаётся материалу следующими путями:

• •    возбуждение электронов во внешних оболочках (вторичные электроны с низкой энергией, обычно 1-50 эВ);

• •    возбуждение основных электронов (электроны Оже и характеристические рентгеновские лучи);

• •    первичные электроны, замедляющиеся непрерывно (непрерывные рентгеновские лучи);

• •    взаимодействие с решёткой (фотонное рассеивание, может быть обнаружено через энергетические потери).

Эти процессы рассеивания являются причиной перемещения первичных электронов в материале зигзагообразным образом и их замедления, пока они не будут рассеяны назад через поверхность или поглощены материалом.

Испускаемые электроны с низкой энергией, известные как вторичные электроны (secondary electrons – SE), формируемые возбуждением элементов поверхности на глубине 5-10 нм с энергией менее 50 эВ, используются в СЭМ для воспроизведения топографии. Генерация вторичных электронов происходит в результате столкновений первичных электронов с внешними электронами атомов (рис. 2). Область генерации вторичных электронов близка к исследуемой поверхности. Число вторичных электронов больше числа первичных электронов.

Упруго рассеянные первичные электроны (рис. 3), часто называемые обратно отражёнными электронами (BSE, backscattered electrons), образующиеся во всём объёме с энергиями 50 эВ < Е < Ее-луча , используются для получения информации о химическом составе и кристаллической структуре. Часть первичных электронов поворачивается электромагнитным полем ядра, и, если угол рассеивания больше 180º, электрон может выйти назад через поверхность.

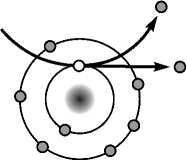
Рис. 2. Схематичное изображение генерации вторичных электронов

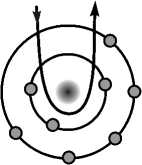
Рис. 3. Схематичное изображение генерации обратно отражённых электронов

Также отличают генерацию вторичных электронов обратно отражёнными электронами (SE2), возвращающимися к поверхности после ряда неупругих столкновений (рис. 4).

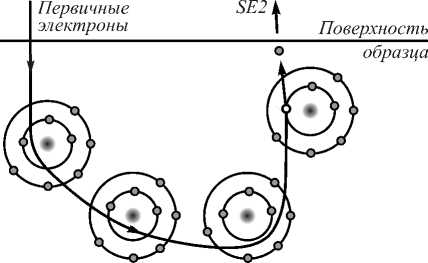
Рис. 4. Схематичное изображение генерации вторичных электронов SE2

SE2 приходят из области поверхности большей пятна первичных электронов. Поэтому разрешение намного хуже, чем при использовании только вторичных электронов.

Характеристическое рентгеновское излучение может быть использовано для качественного и ко- личественного анализа элементного состава и распределения в образце.

Оже электроны из области образца размерами менее 5 нм несут элементную и химическую информацию.

Видимый свет (катодолюминесценция) даёт информацию об электронных/оптических характеристиках, запрещённой зоне.

Общее правило для всех видов интерпретации изображения СЭМ – микроскоп показывает образец, как если бы он освещался детектором и наблюдался глазом в апертуре. Различие в яркости между двумя областями может интерпретироваться как различия углов поступающего первичного пучка, направлений к детектору, атомного веса, химических свойств поверхности, кристаллографических свойств, микротопографии.

Хотя электронная микроскопия позволяет увидеть образцы с очень высоким увеличением, она имеет свои побочные эффекты. Во-первых, изображения, особенно полученные в ПЭМ, сильно зашумлены. Вторая проблема заключается в расфокусировании изображения, что сильно проявляется при высоких увеличениях. Дополнительные проблемы: вибрация и скапливание заряда. Вибрация вызывается перемещением образца в процессе сканирования электронным пучком. В основном этот эффект проявляется на краях образца в виде развевающегося флага. Скапливание заряда можно разделить на четыре типа в соответствии с [6]. К ним относятся: артефакты взаимодействия пучка, загрязнение, артефакты изображения (скапливание положительного и отрицательного заряда) и спонтанное излучение.

Артефакты взаимодействия пучка наблюдаются в виде эффекта «рыбий глаз»: некоторые области имеют большее увеличение, чем остальная часть изображения. Это вызывается зарядами, скапливающимися на поверхности образца из-за плохого заземления. Скапливание положительного заряда означает, что есть положительное электрическое поле на поверхности образца, в результате чего понижается общий контраст изображения. Скапливание отрицательного заряда приводит к противоположному результату, изображение становится более ярким. Загрязнение – это результат осаждения инородных углеродных веществ, возникающих от разложения углеводородов в самом образце. Этот эффект отображается в виде прямоугольной области после её сканирования. Спонтанное излучение представляет собой явление, возникающее как результат случайной эмиссии электронов из образца. Это излучение зависит от длительности разряда и видно на изображении в виде полос в направлении сканирования.

Формирование изображения

В ходе развития электронной микроскопии различные подходы применялись для улучшения качества изображений. Большинство из них было основано на усовершенствовании технических средств. Радиально- симметричные линзы широко использовались в электронных микроскопах, но хроматические аберрации первого порядка и сферическая аберрация третьего порядка ограничивали разрешение электронных микроскопов. В 1936 Scherzer [7] показал, что хроматические и сферические аберрации статических круглых линз всегда положительны при распространении пучка в незаряженной области. С другой стороны, при отказе от круговой симметрии могут быть получены отрицательные коэффициенты аберрации для компенсации коэффициентов хроматической и сферической аберрации круглой линзы до нуля. В 1948 Gabor [8, 9] предложил использовать голограмму для коррекции изображения при сильной аберрации линз. В этом случае устраняется негативное влияние недостатков оптических элементов на изображение в последующем шаге восстановления.

Цифровая обработка изображений вскоре продвинулась далеко за пределы голографического восстановления. В конце 1960-х и в 1970-х годах трёхмерная реконструкция и фазовая проблема были основными задачами обработки изображения [10]. После включения коррекции сферической аберраций в стандартные процедуры появились другие подходы к восстановлению выходной волны [11, 12]; в то же время применение коррекции в электронной томографии представляется трудной задачей [13].

Изображения, полученные с помощью электронного микроскопа, являются аппроксимациями идеальных 2D проекций наблюдаемых 3D структур. Результатом таких факторов, как аберрации линз, рассеяние электронов и дефокусировка, являются изображения, не представляющие истинные математические проекции. Такие изображения напоминают свёртку идеальной проекции с функцией рассеяния точки (ФРТ). Функция рассеяния точки (или размытие) - это отклик изображающей системы на предмет в виде точечного источника.

Упрощённо процесс формирования изображения может быть формально записан как двумерная свёртка истинного изображения с ФРТ изображающей системы в виде:

f = f * h + n , (2)

где f – полученное изображение, f – истинное изображение, h – ФРТ, n – шум наблюдения, * - дискретный 2D линейный оператор свёртки.

Помимо управляемых геометрических размеров зонда, таких как размер сфокусированного пучка электронов, углов его сходимости и расходимости и глубина фокусировки СЭМ пучка, как уже упоминалось, на ФРТ влияют факторы взаимодействия пучка с материей, меняющиеся со временем: скапливание заряда, вибрация. Поскольку получение изображения в СЭМ предполагает сканирование пучком по образцу с конечной скоростью, ФРТ в каждой точке растра будет разной. В дальнейшем изложении рассматривается случай не меняющейся со временем ФРТ для СЭМ.

Для 2D некогерентно освещённой изображающей системы с увеличением M функция интенсивности v ( x 2 , y 2 ) в плоскости изображения представляется как интеграл свёртки [14]:

^V ( ^x 2 , У 2 ) =

= U h ( Х 1 - Mx 2 , У 1 - My 2 )| ² v ( X 1 , У 1 ) d x i d y i ,

дулирует амплитуду и фазу изображения дифракции электронов сформированного в задней фокальной плоскости линзы объектива. КПФ зависит от коэффициента сферической аберрации линзы объектива; длины волны, определяемой ускоряющим напряжением; степенью дефокусировки, пространственной частотой.

где v ( x_i, y_i ) - функция интенсивности в плоскости объекта и h ( x , y ) – комплексная ФРТ. Поскольку в (3) используется функция рассеяния точки по интенсивности h ( x , y )| , фазовых множителей в (3) нет. В частотном пространстве можно записать:

V ( k x , k y ) = C ( k x , k y )V ( k x , k y ) и

^V ( ^x 2 , У 2 ) =                                               ⁽⁴⁾

= JJ ^{V ( k} x , ^k y ) exP [- i² " ( ^k x ^Mx 2 ^{+ k} y ^My 2 ) ] ^{d k} x ^{d k} y ,

Устранение шума

В основном устранение шума производится с помощью сглаживающих фильтров, таких как размытие по Гауссу и сглаживание по прямоугольному окну.

В усечённой свёртке инверсной фильтрации для некогерентно освещённых изображающих систем стандартная процедура обращения свёртки заключается в инвертировании (3) [14]:

^v ( x i , y i ) = F ^{- i}

где V^ɶ , V и С – 2D преобразования Фурье vɶ , v и h ² соответственно, так что

f V ' ( k x , k y ) ^ l C ( k x , k y )

c ( k x , k y ) =

= JJ | h ⁽ x i , Л ’! )!² exP ^{[ i2 n} ( k x x i ⁺

Mi ) ] d x i d У г

Традиционно С называется оптической передаточной функцией (ОПФ), V – пространственный спектр интенсивности изображения и V – пространственный спектр интенсивности объекта.

Для 2D когерентно освещённых изображающих систем комплексная функция изображения й ( x ₂, у ₂ ) может быть выражена как свёртка комплексной функции объекта й ( x_i,y _i ) и комплексной ФРТ [14]:

й ( x 2 , У 2 ) =

= JJ h ( x 1 - Mx ₂, y _i - My ₂ ) u ( x_i, y _i ) d x _id y _i.

В Фурье-пространстве это записывается как:

U(kx, ky) = c(kx, ky)U(kx , ky) и u ( x 2, У 2 )=                                           (7)

= JJ ^{U (} k x , k y ) exP ^{[- i2 n} ( ^k x ^Mx 2 ⁺ k y My 2 ) ] ^d k x dk У ,

где U , U и c – 2D Фурье-преобразования uɶ , u и h – соответственно, так что

c ( k x , k y ) =

= JJ ^{h (} x i , У 1 ^)ехР [ ^{i2 n} ( ^k x ^x i ⁺ Mi ) ] d x i d У г

Таким образом, с называется контрастной передаточной функцией (КПФ), U – комплексный спектр изображения и U – комплексный спектр объекта. КПФ часто используется в ПЭМ высокого разрешения для оценки и сравнения разрешения и предела увеличения различных микроскопов. КПФ мо-

= JJ ^V ( ^k x , k y ) exP ^[ i ^{2 n} ( kxx i ⁺ k y y i ) ] ^{d k} x d k y .

Вместо V ( k_x , k_y ) в дроби вводится V ‘ ( k_x , k_y ) с фильтром низкочастотного пропускания для подавления пространственных частот, связанных с шумом, выше максимальной пространственной частоты k max .

^V '( ^k, , ^k y ) = ^V ( ^k , , ^k y ) ^Г , ma, ( t , , k y ) , ГДС

^Г - ma, ( ^k - , ^. ) =

= <

1, kmax - V kx2 + ky

k -k max s

0,

^ k x + - у ^ k s ,

,   k s <  V k x + k y <  k max ,

J ^k x + k y ^ ^k max .

Целью является сглаживание границ спектральной маски для подавления эффектов наложения.

Кроме этой усёченной свёртки инверсной фильтрации, существует множество усовершенствованных методов [15].

Для когерентно освещённых изображающих систем, так же, как в (8), комплексная функция объекта находится как:

u ( x i , y i ) = F ⁱ

f (7 ‘(kx, ky) l c ( kx , ky )

= JJ ^U ( ^k x , ^k y ) e^XP ^[- i ^{2 n} ( k x x i ^{+ -}у У 1 ) ] dk x ^{d k} y .

Инверсная фильтрация может быть выполнена прямым делением двух комплексных полей U и с . Однако так же, как и в случае использования функции интенсивности, метод инверсной фильтрации в комплексной плоскости вызывает усиление шума для малых величин знаменателя U ‘ ( k_x , k_y )/ c ( k_x , k_y ) , осо-

бенно на высоких пространственных частотах. Соответственно, U '( k_x , k y ) определяется подобно (10)

^U ' ( k x , k y ) = ⁰ ( k x , ^k , ) ^Г k_ ( k x , k y ) . (12)

Действительная часть Г k ( k_x , k y ) может быть равна нулю, аннулируя фазовый вклад в (12). Ширина спектра с соответственно ограничивается так, что отбрасываются только нефизические частоты, связанные с шумом. Однако в свёртке интенсивности требуется применение более сложных методов [15, 16]: малые значения в пределах спектральной ширины также чувствительны к шуму.

Медианная фильтрация также стала популярным инструментом предварительного сглаживания при обработке изображений, поскольку она обладает свойствами сохранения краёв (границ изображения) при удалении шума [17, 18]. Преимуществами медианного фильтра являются его концептуальная простота и минимальное размытие границ изображения. Однако он менее эффективен в удалении Гауссова шума и шума случайной интенсивности, поскольку медианный фильтр может удалять шум при условии заполнения шумовыми пикселями менее половины окрестности области.

В настоящее время более популярны сохраняющие края сглаживающие фильтры, включающие фильтр анизотропной диффузии [19] и двусторонний фильтр [20]. Двусторонний фильтр относительно прост и требует меньших вычислительных ресурсов по сравнению с фильтром анизотропной диффузии. В [21] отмечено, что фильтры анизотропной диффузии и двусторонний тесно связаны друг с другом, несмотря на их отличающееся математическое выражение и оба могут рассматриваться как форма нелинейной диффузной фильтрации. Общие ограничения окрестности этих фильтров – это появление устойчивых областей, вызывающих эффект лестницы [22]. Другим недостатком является невозможность сглаживания импульсного шума [23].

Хороший обзор и сравнение различных фильтров шумоподавления даётся в [24]. В обсуждении отмечается, что Гауссовы фильтры сохраняют только плоские зоны, размывая или удаляя контура и детали изображения. Анизотропная фильтрация сохраняет края прямыми, но вводит артефакты в плоские зоны. Таким образом, они предлагают улучшить оба фактора посредством объединения двух фильтров.

Двусторонняя фильтрация была применена для повышения контрастности и уменьшения шума, что позволило увеличить скорость выбора частиц в различных биологических приложениях электронной микроскопии [20, 25]. Основное отличие двусторонней фильтрации от других фильтров шумоподавления состоит в том, что она учитывает не только область наблюдения изображения, то есть соседство пикселей, но и диапазон значений пикселей, как показано на рис. 5. Фильтр заменяет значение пикселя средним значением подобных величин и значений близлежащих пикселей. В гладких областях он в основном работает как фильтр стандартной области. На краях множитель нормировки исключает пиксели другой стороны края.

б)

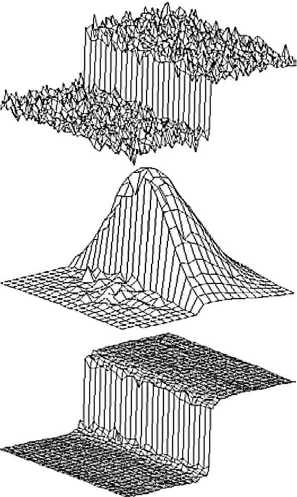
Рис. 5. Работа двусторонней фильтрации: обрабатываемое изображение (а); ядро шумоподавления (б); изображение после обработки (в)

Фильтр записывается в следующем виде:

f ^{( x} ) = g - 1 ^{( x} ) [f f ( £ ) q &^x ) 5 ( f О f ^{( x} ) ) d ^    (13)

с множителем нормировки g ( x ) вида, показанного на рис. 5 б :

g ^{( x} ) = If q ⁽ S , ^x ) ⁵ ( ^f ( S ), ^{f ( x} ) ) d ^ , ⁽¹⁴⁾

где f ( x ) – значение пикселя x в выходном изображении, f ( x ) – значение пикселя x во входном изображении, q ( ^ , x ) - геометрическая близость, расстояние между центром окрестности x и соседней точкой ξ, 5 ( f ( ^ ), f ( x ) ) - близость значений пикселей, разброс значений пикселей между центром окрестности x и соседней точкой ξ.

Двусторонняя фильтрация – это Гауссово размытие с сохранением изображения краёв. Этот алгоритм рассматривает только пиксели, близкие в пространстве и по их значениям. Если значения близки, то двусторонний фильтр работает как Гауссово размытие.

Повышение резкости

Один из самых популярных инструментов для повышения резкости изображения в фотографии - нерезкое маскирование [26]. Этот фильтр резкости включает в себя три операции: размытие оригинала ядром сглаживания; вычисление маски вычитанием размытого изображения из оригинала; сложение маски, умноженной на коэффициент, с оригиналом. Хотя нерезкое маскирование не имеет теоретического обо- снования, на практике оно зарекомендовало свою высокую эффективность в повышении резкости краёв без излишнего увеличения шума.

Если ФРТ известна и шумы незначительны, то восстановить истинное изображение легко. Применение процедуры обратной свёртки основано на теоретической возможности воспроизведения изображения путём удаления эффекта рассеяния точки и шума. Обратная свёртка может быть применена только к размытию, вызванному характерным профилем электронного зонда. В случае электронной микроскопии форма этого профиля известна лишь частично, но иногда и полностью неизвестна.

Процесс определения ФРТ и восстановления неизвестного изображения в условиях отсутствия информации или частичных данных об изображающей системе известен как слепая обратная свёртка [27-30]. Слепая обратная свёртка может быть выполнена итеративно, причём определение изображения и профиля пятна улучшается в каждом шаге, или не итеративно, если профиль пятна получен на основе внешней информации.

Итерационный процесс слепой обратной свёртки может быть описан в соответствии с [27]. Процесс начинается с первоначальной оценки функции рассеяния точки (ФРТ). Далее восстанавливается изображение по рассчитанной ФРТ, и результат сравнивается с зарегистрированным изображением. Оценка ФРТ корректируется поправкой на разницу между двумя изображениями использованием оценки максимального правдоподобия, и процесс начинается с новой оценки. Методы оценки максимального правдоподобия включают обратную свёртку Ричардсона-Люси [31, 32] и ЕМ-алгоритм [33].

Основная идея обратной свёртки Ричардсона-Люси - вычисление в каждой итерации наиболее вероятного изображения по наблюдаемому изображению и определяемой ФРТ и вычисление наиболее вероятной ФРТ по наблюдаемому изображению и определённому изображению. Этот алгоритм является популярным в области астрономии и восстановления медицинских изображений вследствие его надёжности при наличии шума и используется во многих алгоритмах определения ФРТ [34-36]. Основными параметрами являются: форма пятна, размер пятна и число итераций алгоритма. Первые два параметра используются для оценки начальной ФРТ h пятна, определяемой следующим образом:

г

h ( x , y ) = exp

V

i x a+i y 1 1 o “

где α – определяет форму, σ - размер пятна. Для изображений электронной микроскопии форма пятна α = 1,6, что приводит к более острому пику, чем у Гауссова пятна с α = 2. Размер пятна может меняться в соответствии с обрабатываемым изображением.

После определения начального размера пятна алгоритм проходит заданное число итераций. В каждой итерации k из начального изображения g и пятна hk - 1 определяется изображение fk :

fk = fk-1 × f fk-1 hk-1

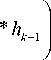
Оцениваемое пятно h_k корректируется с использованием начального изображения g и k -й оценки изображения f_k :

Г -)

h k = h k - 1 × ^f * f k . (17)

V ^fk ^hk - 1 7

EM-алгоритм (expectation-maximization) - алгоритм, используемый для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных [37]. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия, таким образом увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации.

Неитерационные методы включают SeDDaRA [38], использующий информацию о сцене в форме эталонного изображения, и APEX [39], предполагающий, что ФРТ имеет определённую форму, и определяющий ширину формы.

Повышение резкости, однако, имеет свои пределы. Изображения с очень низкой резкостью не могут быть улучшены. Согласно [40], фильтры резкости не могут восстановить подробности, если модуляционная передаточная функция (МПФ) очень мала (менее 10 %). Оценки максимального правдоподобия в итерационных алгоритмах обратной свёртки, как правило, чрезмерно повышают резкость изображения [41]. Это может быть частично скомпенсировано с помощью наложения ограничений на изображение, таких как обеспечение раннего прекращения итерационного алгоритма и выполнение условия неотрицательности изображения. Чрезмерное повышение резкости изображения может привести к возникновению артефактов в виде вибраций по краям. В [42] предлагается метрика оценки вибрации после обратной свёртки.

Согласно [43], целесообразная резкость зависит от величины контраста в прилегающих областях, т.е. можно больше повысить резкость краёв с лучшим воспринимаемым качеством, если окрестные области имеют более высокий контраст.

Заключение

Электронная микроскопия с помощью электронных пучков для сканирования образца позволяет наблюдать объекты с разрешением почти атомного уровня. В работе обсуждаются возможности использования фильтров пост-обработки для улучшения ка- чества получаемых изображений по характеристикам шума и резкости.

Множество подходов разработано для коррекции влияния передаточных функций в процессе восстановления изображений электронной микроскопии. Большинство существующих в настоящее время методов допускают, что весь образец подвергнут размытию одной однородной передаточной функцией. Это предположение приемлемо в случае малости времени получения изображения по сравнению с процессами скапливания заряда, малости разрешения восстановленного изображения, однородности образца по материальному составу и топографии. Изменение размытия в пределах образца становится всё более очевидным с увеличением достижимого разрешения. Поэтому существует необходимость в методах коррекции изображений, учитывающих зависимость передаточных функций от положения в пространстве.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракты № 02.740.11.0805 и № 14.740.11.0016).