Формирование изображений дифракционной многоуровневой линзой

Дифракционная линза имеет ряд преимуществ перед линзой рефракционной по таким параметрам, как масса, размер, простота тиражирования линзы для формирования несферического сходящегося волнового фронта. В связи с этим дифракционная линза интересна как оптический прибор для различных приложений. Большинство имеющихся работ, как правило, рассматривают дифракционную линзу либо как дополнительный элемент для компенсации хроматической аберрации рефракционной изображающей системы [1, 2], либо для фокусировки [1–11], например в [3, 4] рассматривается осевое распределение интенсивности для когерентного случая. В [5] рассматривается процесс фокусировки плоской волны на линзе Френеля. Много работ посвящено частным случаям использования дифракционных линз в узкоспециализированных задачах [6–11]. В частности, в работе [6] изучаются спектральные свойства дифракционной линзы. Синтез многофокусных дифракционных линз исследуется в работах [7, 8]. В статье [9] рассматривается возможность использования дифракционной линзы в конфокальном микроскопе. Новая модификация бинарной дифракционной линзы предлагается в [10]. В работе [11] рассматривается использование дифракционной линзы для формирования световых пучков.

Исследований применения дифракционной линзы для формирования изображений значительно меньше. При этом, как правило, основное внимание уделяется особенности изготовления такой линзы [12– 14], а не качеству формирования изображения. Кроме того, существенно ограничивается спектральный диапазон [14].

В настоящей работе рассматривается формирование изображений в некогерентном свете с помощью дифракционной линзы. В некогерентном случае объект во входной плоскости представляется как набор точечных источников, от которых в параксиальном случае распространяется параболическая волна, а в непараксиальном – сферическая.

1.    Моделирование: непараксиальный случай

В этом случае от каждого точечного источника на объекте идёт сферическая волна до оптического элемента, расположенного на расстоянии z 1 от объекта:

exP ( ^ik'l ( S^- x nm У + ( n^- У пт ^ + ^Z 12 )         (1)

^A nm        /            Z                Z             ,

V(^-Xnm ) +(П-Упт ) + Zy

где (xnm, ynm) – координаты (m,n)-го точечного источника в объектной плоскости, Anm – соответствующая амплитуда.

Если оптический элемент является дифракционным, то его фаза рассчитывается с учётом базовой длины волны % 0 . При освещении дифракционного оптического элемента (ДОЭ) излучением с длиной волны % комплексная функция пропускания ДОЭ рассчитывается следующим образом:

Поле в плоскости изображения на расстоянии z ₂

от оптического элемента вычисляется с помощью интегрального преобразования Рэлея–Зоммерфельда:

Fnm ( u, v, z 2 ) = —   J JT% (^, П) Snm (^ П)Х%

exp x---

i 2- Й- u ) 2 + ( П- v ) 2 + z 2 %

^Г ( ^- u )² + ( n- v ) 2 + z 2 ¹

d ^ d n ,

где Q - область определения поля в плоскости оптического элемента.

Интенсивность в плоскости изображения:

A     Г 2 п 7

P nm ^{( S} , n , Z 1 ) = — exp I i— Z 1 I x

Z 1       I A   7

Функция Ф принимает любые значения, причём

mod _2п Ф периодичен по 2 п и также Q [mod _2п Ф] перио

^{X eX}P Г     ^[ ( ^S- x nm ) ^{2 +} ( n^- У пт ) ^{2 ]}

I A z A                    ^J

дично по 2 п . Следовательно, (10) можно разложить в ряд Фурье [16]:

Поле в плоскости изображения на расстоянии z ₂ от оптического элемента вычисляется с помощью интегрального преобразования Френеля:

T q ( S , n ) = exp { iQ [ mod 2n Ф ] } =

= E C p exp [ i Ф P ] = E C p exp [ i ф ( S , n ) P ] , pp

^F nm ( u , v , z 2

) =^- A ^eXP [ i ^ z 2 I^X J J T A^ , П ) ^{A z} 2     V ^A 7 q

^{X P} nm ( ^S , П , ^z 1 ) ^eXP

^Ц ( £- u )² + ( n- v )² ) d S d n . A z,

C p = 2 П 2 [ exp { iQ [ mod 2n ° ] } exp [ - i Ф P ] d Ф .    <12)

После освещения ДОЭ (10) волной A ( S , n ) поле на

расстоянии z ₂ от оптического элемента вычисляется с помощью интегрального преобразования Френеля (6):

Выражение (6) удобно как для теоретического

анализа, так и в вычислительном плане, так как позволяет применить алгоритм быстрого преобразования Фурье (БПФ).

В частности, если подставить P nm ( S , n , z 1 ), то лучим:

по-

F ( u , v , z ₂

x i        [.2п

) = ^-г" ^ex p I ^Z V A z 2     V A

x JJ a ( S , n ) T q ( S , n ) x q

F nm ( U , V , ^Z 2 ) =— ,

1 z 2

. 2п / x exp i -(Zi + z2 ) x

i п / _{2      2} x          i п

^X exp AZ ⁽ x nm ⁺ y nm ) exp AZ

( u ² + v ² ) ^x

^                  IГ 1^1

xj [Ta(S,n)exp' —(S +n )I +Itx

A

—^                                     \ 12

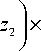
^{x ex}p ^^ ( ^{( S —} u ⁾² + ⁽ n^- v ⁾² ) d ^S d n . A z.

С учётом (11) выражение принимает следующий вид:

Г. 2 п

F ( u , v , ^z 2 ) = ^exp I I— ^z 2 | E c p G p ( u , ^V , ^z 2 ) ,      ⁽¹⁴⁾

V ^A 7 P

где G p ( u , v , z 2 ) = - -i - J J A ( S , n ) exp [ i ф ( S , n ) P ] x

Az r 2 q n                    (15)

x exp

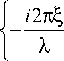
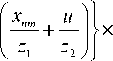
^{x ex}p ^(й^- u ^{)2 + (} n^{- v )2} ) d ^S d n . A z.

x exp

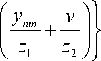
d S d n .

В случае аналитического задания T _A ( S , n ) это ^вы" ражение можно приближённо вычислить методом стационарной фазы [15]. Если же функция ДОЭ (2) представляет собой квантованный (дифракционный) аналог гладкой аналитической функции, то для вычисления интеграла (7) можно воспользоваться разложением в ряд Фурье, как показано ниже.

2.1. Квантованные ДОЭ

Запишем фазу тонкого (дифракционного) элемента в виде:

ф t ( S , n ) = mod 2n ^ ( S , n ) ,

где ф t ( S , n ) e [ 0,2 п ] .

Тогда квантованную фазу обозначим:

ф q ( S , n ) = Q [ф t ( S , n ) ] ,                             (9)

где преобразование Q такое, что Q [0] = 0, Q [ 2п ] = 2п, причём монотонно возрастающее.

Комплексная функция пропускания оптического элемента в этом случае:

T q ( ^S , n ) = ^exp ^[ i ф q ( ^S , n ) ] =

= ^eXp { iQ [ ^mod 2n ф ( ^{S ,} n ) ] } = ^exp { iQ [ ^mod 2n ^ф ] } .

Так как выражение (15) содержит под знаком интеграла гладкие аналитические функции, то его можно вычислить методом стационарной фазы.

Фаза быстроосциллирующей функции в (15) имеет следующий вид:

f_P ( S , n ) = ф ( S , n ) P + 7^"^[ ( S- u ) ² + ( n- v ) ^2] =

A z 2

2 п[         . ^{[( S- u )2 + (} n^{- v )2 ]}

= T I *    -- 2 z-------

z_s X ф ( S , n ) A P где * p ( ^S , n ) = ^X '

2 п

.

Определим стационарную точку:

' d f p ( ^S , n ) = dy P ( ^S , n ) ₊ ( S- u )

dS

^{dS         z} 2

= 0,

'

^d f p ^(S , n ) = ^d* P ^(S , n ) ₊ ( n- v ) = ₀.

dn dn

Из (17) следует:

"u, ( S,n )- . 2. ^Э* ^Р^

' v , ( S , n ) = z 2 5*^

z ₂

+ S ,

+ n .

,

Выражение (15) приближённо равно:

i        I i п I

Gp (u.v,z2) =--expl — Ix z 2     V 4 I

x

2 п

A ( ⁵ s . n s ) exp l H-f p ( ⁵ s . n s ) I

V 1          у

d 2 f p ( 5 . П ) d ² f p ( 5 . n ) I d ² f p ( 5 . n ) Y d^ ² dn ² V ^n ,

№ s .n s )

где ( 5 s . n s ) - стационарная точка из (17).

Используя (18), выразим знаменатель в (19) через координаты выходной плоскости.

Из (18) имеем следующее соотношение.

'^d u p ( ^ . n )       ^d 2 V p ( ^ . n )

d5z2

sv^=z 2 a2 v, ..-+, dndn

Тогда вторые производные в (19) с учётом (17) и (20):

d ² f p ( 5 . n ) = d 2 V p ( 5 . n ) + £ = £ d U p ( 5 , n ) d^ ²     = d5 ^{2     +} z ₂ = z ₂ d5

d2fp (5,n) = Э2Уp (5,n) + X = X 5vp (5,n) dn2          dn2      z2 z2

Соответственно, смешанные производные:

d ² f p ( 5 . n ) = d ² V p ( 5 . n ) = I d U p ( 5 , n )

d5dn        d5dn     z 2    d5

^d 2 f p ( ⁵ . n ) = 5 ² v p ( ⁵n ) = X ^{d v} p ( ^n )

dnd5       dnd5     z 2   dn

Таким образом, выражение (19) принимает следующий вид:

I i ^п I., G p ( u . v . z 2 ) =- i exp I — I x

I F ( ^u . ^v . ^z 2 )|² = E| cp |² Gp ( ^U . ^V . ^z 2 )|² .                ⁽²⁵⁾

p

• 2. 2. Освещение ДОЭ монохроматическим излучением

Фазовый дифракционный оптический элемент, изготовленный в подложке с показателем преломления n для базовой длины волны 1 0 . имеет глубину микрорельефа, связанную с фазовой функцией (8):

h _{(? n)} = ¹ o ^mod 2n V ( ⁵ . n ) = ^ о Ф t ( ⁵n ) .          2 п ( n - 1 )         2 п ( n - 1 )

.

При освещении такого элемента монохроматическим излучением с длиной волны 1 фазовая функция прошедшего поля будет следующей:

2 п

ф ( 5 . n . 1 ) = f ( n — 1 ) ^h ( 5 . n ) =

,          ¹                                      (27)

=     m^od ;n ^ ( 5 . n ) .

Для квантованного ДОЭ аналогично:

Ф q ( 5 . n . 1 ) = - QQ [ mod 2п ф ( 5 . n ) ] .             (28)

В этом случае также комплексную функцию пропускания можно представить через ряд Фурье:

T q ( 5 . n . 1 ) = exp I i ^{1 1} Q [ mod 2n ф ( 5 . n ) ]l =

L ¹                     J (29)

= E c p ( ¹ ) exp [ i ф ( ⁵ . n ) p ] .

p

Найдём коэффициенты разложения для фазовой функции Ф = ф(5.n) :

1 2?    I 1I c (1) = — fexp l i—Ф | exp (-ipФ) dФ.(30)

2п0    V 1I

x

( 2П , V

A ( ⁵ s . n s ) exp l i^f p ( ⁵ s . n s ) I

V ^          |

1 2п     Г cp (1)=t" J exp i l у

2 п 0     [ V 1

p IФ d Ф =

d U p ( 5 . n ) d V p ( 5 . n ) -1 d U p ( 5 . n ) I \ d5 dn V dn J

(⁵ s .n s )

= ^exp i ^п V _T^- P

sin

п

1 o

p

Интенсивность поля (14):

п

1 o

p

.

| F ( u . v . z ₂ )| ² =

E c p G p ( ^U . ^V . z 2 )

p

= E I c p |² G p ( ^U . ^V . z 2 )|^{2 +                            (24)}

p

⁺ E c i c m G ( ^u . ^v . z 2 ) G m ( ^u . ^v . z 2 ) . l , m

При освещении объекта частично-когерентным светом вклад перекрёстных членов в (24) будет мал, поэтому

Из (31) следует, что при освещении ДОЭ излучением с длиной волны, отличной от базовой, число дифракционных порядков будет зависеть от отношения длин волн.

В частности, пусть оптическим элементом служит параболическая линза с фокусным расстоянием f 0 :

ф ( 5 . n )

2 п ( 5^+22)

1 o 2 f o

Тогда поле (6) примет следующий вид:

i      Г.2n )

^F nm ( u , V , z 2 ) = -T— exP I ' V z 2 I ^X

AZ 2    V A 7

^X Z cP ( ^X ) JJ exP ^- i P n

2n (^2 +П2)

A o 2 f , p

X

^{X P} nm (^ П , z 1 ) exP ^⁽ Й^- u ) 2 ^{+ (} П^{- V} ) 2 ) <7 M A z 2

Рассмотрим первую экспоненту под интегралом в (33):

exp

2 n ( ^ 2 ⁺П ² ) ip

A o    2 f ,   ^P

= exp

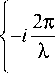
(52 +n2)

2 f , /(A p /Ao )

Рассматривалось освещение лазерным излучением с тремя длинами волн: A 1 = 400 нм, A ₂ = 550 нм и A 3 = 700 нм. Базовой считалась средняя длина волны A _o = A 2 . Изображение рассчитывалось на различных расстояниях от линзы размером 0,5 X 0,5 мм.

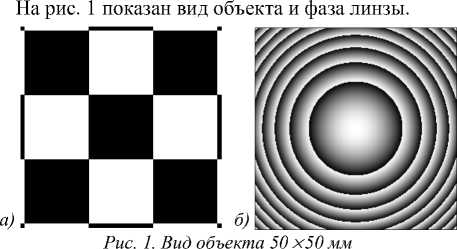
и фаза линзы диаметром 5 мм

Из выражения (34) очевидно появление кратных фокусов fp = f> /(Ap/Ao).

3.    Результаты численного моделирования

Моделирование выполнялось как в рамках непараксиальной модели (3), так и параксиальной модели (6) на основе алгоритма БПФ.

При моделировании были использованы следующие параметры. Объект общим размером 50 X 50 мм имел характерные детали размером 16 X 16 мм. Для формирования изображения использовалась линза с фокусным расстоянием f =320 мм и диаметром 5 мм, расположенная на расстоянии z ₁ =50000 мм от объекта.

• 3.1.    Дифракционная многоуровневая линза

В табл. 1 показаны результаты моделирования для идеальной линзы (действует аналогично рефракционной).

В первой строке таблицы приведены результаты расчёта на основе выражения (3). Как видно из результатов табл. 1, в этом случае идеальная линза примерно одинаково хорошо изображает объект при освещении излучением с различными длинами волн. Некоторое различие в резкости связано с изменением функции рассеяния точки при изменении длины волны. Хроматическая аберрация, связанная с изменением показателя преломления материала, из которого изготовлена линза, в этом случае не учитывалась.

Табл. 1. Сравнение моделирования формирования изображения в параксиальной и непараксиальной моделях для идеальной линзы на расстоянии 322 мм от линзы

Расчёт с использованием алгоритма БПФ по формуле (7), показанный во второй строке табл. 1, качественно совпадает с более точным расчётом, однако несоответствие геометрии изображения и дискретизации (необходимость выполнять интерполяцию) приводят к расплыванию формируемых изображений.

На рис. 2 и в табл. 2 показаны результаты моделирования построения цветных изображений для 256уровневой дифракционной линзы, рассчитанной для базовой длины волны A 2 .

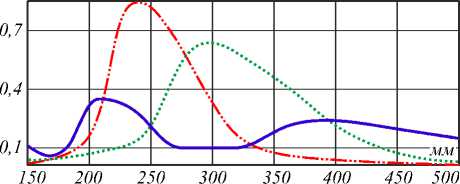
Рис. 2. Распределение интенсивности на оптической оси для многоуровневой дифракционной линзы (синий цвет для Л1 400 нм, зелёный цвет для А2=550 нм, красный цвет для А3=700 нм)

Из рис. 2 хорошо видно смещение фокуса и появление дополнительных фокусов при изменении длины волны освещающего излучения по сравнению с базовой длиной волны, для которой изготавливается ДОЭ.

В соответствии с (35), фокусные расстояния вычисляются по формуле:

f . p = f , 1 0 /( 1 p ) .                                 (36)

Для рассматриваемых параметров расчёта фокусы: f 7oo, _p = 320 мм • 550 нм/( р • 700 нм) = 250 мм/ p , f_{4 00}, p = 320 мм • 550 нм/( p • 400 нм) = 440 мм/ p .

На рис. 2 хорошо виден смещённый фокус для красного излучения f_{7 00},1 = 250 мм и два фокуса для синего: f_{4 00},1 = 440 мм, f_{4 00},₂ = 220 мм.

Табл. 2. Сравнение моделирования формирования изображения в параксиальной и непараксиальной моделях для многоуровневой дифракционной линзы на расстоянии 322 мм от линзы

1 1 =400 нм

1 2 = 550 нм

Непараксиальный расчёт

Параксиальный расчёт (БПФ)

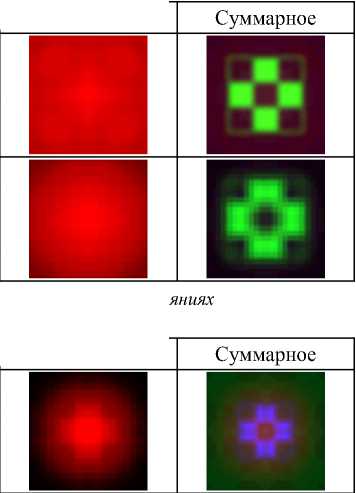
Табл. 3. Моделирование формирования изображения на различных рассто от многоуровневой дифракционной линзы (расчёт на основе БПФ)

z =220 мм

1 1 =400 нм

1 2 = 550 нм

1 ₃ = 700 нм

1 ₃ = 700 нм

z =250 мм

z =294 мм

z =322 мм

z =440 мм

Из результатов табл. 2 следует, что дифракционная линза подвержена существенным хроматическим аберрациям. Учитывая качественное согласование результатов расчёта на основе алгоритма БПФ с более точной моделью при значительном сокращении времени расчёта, будем использовать этот алгоритм для предварительных оценок.

Ниже показан расчёт формирования изображения на различных расстояниях от линзы.

• 3.2.    Квантованная линза

4.    Эксперимент

Изготовление многоуровневых дифракционных элементов довольно сложно. На практике чем меньше уровней квантования, тем проще технологический процесс. Наиболее простыми в изготовлении являются бинарные элементы.

На рис. 3 показаны результаты моделирования для бинарной дифракционной линзы. Из рис. 3 видно, что расположение фокусов для различных длин волн осталось примерно таким же, как и для многоуровневой линзы, однако интенсивность в фокусах упала более, чем в 2 раза (теоретически остаётся 41,5 %). Это произошло из-за перераспределения энергии в дополнительные дифракционные порядки (локальные фокусы) [4].

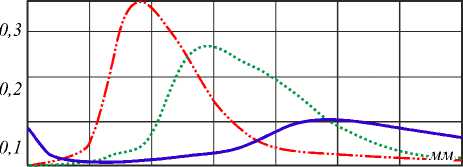
150   200   250   300    350   400   450 500

Рис. 3. Распределение интенсивности на оптической оси для бинарной дифракционной линзы (синий цвет для λ ₁=400 нм, зелёный цвет для λ ₂=550 нм, красный цвет для λ ₃=700 нм)

Для проведения экспериментов по формированию изображений дифракционными линзами было изготовлено методом фотолитографии несколько вариантов дифракционных линз. В частности, были изготовлены бинарные линзы с фокусным расстоянием 50 мм и четырёхуровненевые линзы с фокусными расстояниями 16 мм, 50 мм, 160 мм, 320 мм. При этом для формирования четырёхуровневого микрорельефа осуществлялась последовательная запись трёх фотошаблонов на одной подложке с промежуточным плазмохимическим травлением [17–19]. Глубина сформированного микрорельефа менялась от 800 нм до 1000 нм, в зависимости от того, на какую основную длину волны рассчитана изготавливаемая линза.

На рис. 4 представлены восстановленная форма микрорельефа центральной области (рис. 4 а ) и сечение профиля одной из таких линз (рис. 4 б ).

Как видно из рис. 4, получившийся микрорельеф хорошего качества без сбоев и неоднородностей. Чтобы проверить работоспособность изготовленных линз, была собрана оптическая схема, представленная на рис. 5.

Для исследования хроматических аберраций дифракционной линзы было использовано несколько специальных цветных таблиц, которые либо распечатывались на бумаге, либо непосредственно выводились на монитор компьютера (рис. 6). Затем в оптической схеме, представленной на рис. 5, осуществлялось формирование изображения, причём настройка на резкость осуществлялась по зелёному цвету.

Как видно из рис. 7, качество изображения весьма невысокое, т.к. в дополнение к хроматической аберрации такая линза обладает ещё и высоким коэффициентом светорассеивания. При использовании четырёхуровневой линзы качество изображения заметно меняется в лучшую сторону (рис. 8).

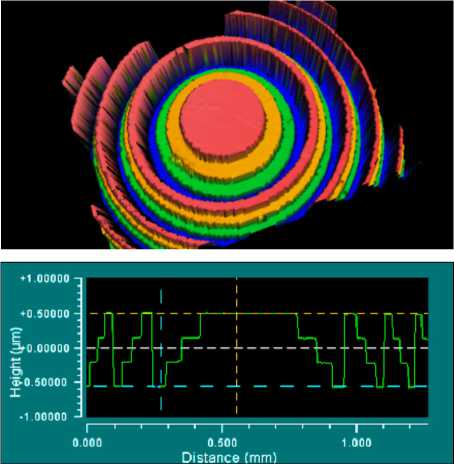
Рис. 4. Восстановленная форма микрорельефа центральной области (а) и сечение профиля одной из таких линз (б), полученные на интерферометре белого света New View Zygo 5000

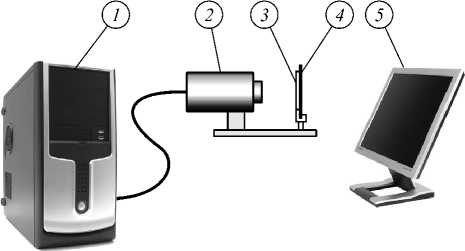
Рис. 5. Оптическая схема, позволяющая строить изображения с помощью дифракционных линз:

1 – компьютер, 2 – CCD-камера, 3 – диафрагма,

4 – дифракционная линза, 5 – монитор

На рис. 7 представлена картина, полученная с помощью бинарной дифракционной линзы.

Несмотря на несомненно высокую хроматическую аберрацию, качество изображения, получаемого на 4–уровневой линзе, существенно выше, чем у бинарной линзы. Ещё более качественным получается изображение при уменьшении спектрального диапазона для формируемого изображения. Так, на рис. 9 представлено изображение рабочего окна программы Windows Comander, снятое с экрана монитора дифракционной четырёхуровневой линзой с фокусным расстоянием 50 мм с расстояния в 1 м.

Как видно из рис. 9, качество полученного изображения близко к качеству изображения, которое получается при использовании хорошего рефракционного объектива. На рис. 10 приведены отдельно цветные квадраты для красного, синего и зелёного цветов.

Как видно из рис. 10, при чётком изображении одной из трёх цветовых компонент две другие существенно размываются.

Рис. 6. Цветные таблицы для контроля хроматической аберрации дифракционной линзы

Рис. 7. Изображение, полученное с помощью бинарной дифракционной линзы

1 2014_06_19_02 а

2014_06_19_02 b-posl 2014_06_19_03 а 2014_06_19 03 .b-posl 2014_06 2Б01 а

; 2014_06_26_01_b

2014_07_03_01 а 2014 07 03 П1 ы^1К

Рис. 8. Изображения цветных таблиц (рис. 6), полученные с помощью дифракционных четырёхуровневых линз

Рис. 9. Изображение рабочего окна программы Windows Comander, снятое с экрана монитора дифракционной четырёхуровневой линзой с фокусным расстоянием 50 мм с расстояния в 1 м

Рис. 10. Увеличенное изображение участка цветной таблицы

Заключение

Методом вычислительного и натурного экспериментов рассмотрено формирование цветных изображений с помощью дифракционных бинарных и четырёхуровневых линз. Теоретически и экспериментально показано, что:

• 1)    изображения, полученные с помощью бинарной линзы, имеют качество совершенно недостаточное для формирования цветных изображений;

• 2)    изображения, полученные с помощью четырёхуровневой линзы, формируют существенно более качественное изображение, однако качество сформированного изображения из-за сильного хроматизма также недостаточно для использования в изображающих системах, кроме случая построения изображения в узком спектральном диапазоне;

• 3)    для работы с цветными изображениями необходимо использование квазидифракционных или гармонических линз [20–22].

Работа выполнена при поддержке Министерства образования и науки РФ и РФФИ (грант № 13-07-13166-офи_м_РЖД).