Формирование эффективного портфеля проектов предприятия машиностроительной отрасли

Введение. Общие вопросы математического моделирования в проектном менеджменте

На сегодняшний день теория управления проектами является быстро развивающимся разделом теории управления социально-экономическими системами. Выделяются несколько направлений в управлении проектами:

– модели календарно-сетевого планирования и управления, с появлением которых и началось управление проектами;

– «качественный» подход к управлению проектами, близкий по своей методологии к менеджменту организаций и развиваемый в основном зарубежными учеными;

– «количественный» подход, основанный на анализе и синтезе математических моделей механизмов управления проектами (процедурах принятия управленческих решений) и развиваемый в основном отечественными учеными [12].

Моделирование является систематизированным способом увидеть варианты будущего и определить потенциальные последствия альтернативных решений, для последующего их сравнения.

Под математическим моделированием понимается процесс установления соответствия реальному объекту некоторого математического объекта, называемого математической моделью, и последующее исследование модели для получения характеристики реального объекта. Вид математической модели зависит от природы реального объекта, задач исследования, требуемой достоверности и точности решения. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности [10; 14].

В научной литературе выделяются следующие этапы построения математической модели:

• 1.    Формализация предмета и цели моделирования, определение границ исследования, основных характеристик предмета исследования.

• 2.    Выбор языка (аппарата) моделирования.

• 3.    Выбор переменных, описывающих состояние системы и существенные параметры внешней среды, включая шкалу их измерения и критерии оценки.

• 4.    Выбор ограничений, как множества возможных значений переменных, и начальных условий (начальных значений переменных).

• 5.    Определение связей между переменными с учетом всей имеющейся о моделируемой системе информации, а также известных законов, закономерностей и т. п., описывающих данную систему. Этап называется «построение модели».

• 6.    Исследование модели, как имитационное, с возможным применением методов оптимизации, решение задач управления. Этап называется «моделированием».

• 7.    Изучение устойчивости и адекватности модели [14].

При управлении проектом могут быть использованы несколько математических моделей, вид и структура которых определяются задачами проекта и наличием информации для принятия решений. Применение математических моделей в проектном менеджменте позволяет:

• –    упорядочить систему информации о проекте на каждом этапе его реализации;

• –    выработать требования для подготовки и корректировки информации с целью решения задач по оптимальному управлению проектом;

• –    обеспечить повышение точности расчетов;

• – обеспечить проведение углубленного количественного анализа проблем и факторов, влияющих на эффективность реализации проекта;

  – оценить последствия изменения условий функционирования проекта и своевременно выработать корректирующие воздействия.

В последнее время в литературе все больше внимания уделяется особенностям управления проектами с позиций различных заинтересованных сторон. Использование данных моделей направлено на повышение эффективности деятельности стейкхолдеров, генконтрактора, заказчиков, что должно обеспечить системность, целостность и адекватность принимаемых решений [1–5].

Используемые математические модели в проектном менеджменте можно разделить на следующие виды:

– организационные – применяются при разработке организационных структур проектов, описывают организационные связи и отношения между участниками проекта в виде систем математических уравнений и неравенств;

– сетевые модели (графики) – известно более 200 сетевых моделей, различающихся по назначению, элементам описания, алгоритмам и др. Созданные в 1960-х гг. модели являются графоаналитическими, позволяют описывать весь процесс от зарождения идеи проекта до его реализации. Наибольшей ценностью обладает метод критического пути, позволяющий оптимизировать график производства работ во времени с учетом ограничений на выбранные ресурсы [6];

– управление ресурсами – позволяет определять оптимальный уровень закупок материальных ресурсов по проекту. Задачам распределения ресурсов уделяется особое внимание, так как они относятся к сложным многоэкстремальным задачам. Наиболее известной моделью оптимизации оптимального размера и оптимального времени заказа является модель оптимизации объема поставок [7];

– управление рисками проекта – модели позволяют провести анализ рисков и определить их влияние на эффективность проекта;

– управление стоимостью – используются для оценки стоимости проекта, распространение получили модели прогноза стоимости на основе функционально-стоимостного анализа;

– управление портфелем проектов – исследуют возможность эффективного управления портфелем проектов при заданных ограничениях и соответствию стратегическим целям организации [8].

Математические модели используются для решения следующих задач:

• –    оценка проектов и хода их реализации с точки зрения достижения стратегических целей организации;

• –    формирование эффективного портфеля проектов;

• –    планирование реализации портфеля проектов;

• –    распределение ресурсов организации между проектами портфеля;

• –    оперативное управление портфелем проектов с учетом изменяющихся внешних условий и целей организации [11].

Получили известность следующие математические модели управления портфелями проектов: оценка эффективности проектов, формирование портфеля проектов, планирование процесса реализации портфеля проектов, распределение ресурсов между проектами портфеля, оперативное управление портфелем проектов.

При оценке эффективности проектов первоочередной задачей является выбор критериев, по которым должны оцениваться проекты и их совокупность. Критерии должны отражать существенные и измеримые характеристики проектов и определять степень достижения стратегических целей организации.

В соответствии с утвержденной стратегией организации, по каждому прогнозируемому портфелю проектов разрабатывается максимальное количество вариантов проектов. Этап оценки эффективности проектов предшествует формированию портфеля проектов: на нем отбрасываются заведомо неэффективные проекты, и сокращается число альтернатив по каждому направлению деятельности. Альтернативные варианты проектов могут отличаться друг от друга стратегиями реализации, используемыми активами, участниками и т. д. Таким образом, задача выбора проектов из множества альтернатив сводится к задаче максимизации целевого критерия эффективности.

Модели формирования портфеля проектов разделяются на два класса: однокритериальные и многокритериальные. Однокритериальные модели принятия решений об отборе проектов в портфель по учету неизвестных факторов можно подразделить на детерминированные, стохастические и модели с элементами неопределенности. Модели формирования портфеля в зависимости от вида целевой функции и ограничений разделяются на четыре вида: 1) линейные; 2) нелинейные; 3) динамические; 4) графические.

Общие проблемы проектного менеджмента на предприятиях машиностроительной отрасли

Выделим основные проблемы при управлении проектами на предприятиях машиностроительной отрасли.

Одной из главных проблем является отсутствие ранжирования проектов по степени их влияния на стратегию развития как отрасли, так и предприятия. Проекты, не влияющие или влияющие отрицательно на стратегию, необходимо исключать из портфеля проектов предприятий. Необходима интеграция проектов в стратегический план, что предполагает наличие стратегического плана развития отрасли и предприятия, а также механизма определения приоритета проектов по степени их соответствия стратегии [14–16].

Следующей проблемой является определение критериев оценки проектов, их совокупности в виде портфелей, условий принятия решения о включении проекта в портфель. Критерии должны удовлетворять требованиям: отражение существенных и измеримых характеристик проектов; определение степени достижения стратегических целей организации; учет прогнозной и экспертной информации; возможность согласования мнения различных субъектов (руководителей, подразделений и т. д.), представления которых о значимости проектов и стратегических целях организации могут различаться.

Проблемой является и отсутствие перечня и конкретизированного объема ресурсов, в рамках которых может быть реализован определенный набор проектов. Задача оптимизации портфеля проектов значительно усложняется при наличии ограничения на ресурсы: финансовые, материальные, трудовые и временные. Как правило, такие ограничения присутствуют всегда.

К проблемам необходимо отнести и отсутствие критериев закрытия проектов, что связано с недостаточностью информации при принятии решения о приостановке, продолжении и прекращении проектов.

Таким образом, основной проблемой на предприятиях машиностроительной отрасли является отсутствие методологии портфельного управления проектами, используются лишь некоторые методы проектного менеджмента.

Использование портфельного управления проектами позволяет эффективно управлять ресурсами для реализации стратегически необходимых проектов. Правильный выбор и успешная реализация портфеля проектов является связкой между стратегическим планированием и проектным менеджментом. Использование математических моделей позволит обосновать выделение ресурсов только на те проекты, которые продвигают организацию к достижению стратегических целей [9; 13].

Далее в статье авторы, на основе существующих математических моделей управления портфелем проектов, проведут выбор портфеля проектов для условного предприятия машиностроительной отрасли. Подходы, использованные авторами, могут применяться в качестве образца для предприятий других отраслей.

Сравнение подходов к моделированию портфеля проектов

Для расчета эффективного портфеля проектов примем усредненные значения реализуемых проектов по отрасли. Отбор проектов осу- ществляется в соответствии со следующими признаками:

• –    направленность на достижение конечных, количественно измеримых целей;

• –    ограниченность во времени (наличие начала и окончания);

• –    уникальность и неповторимость целей и работ;

• –    ограниченность по ресурсам;

• –    координированное выполнение взаимосвязанных работ.

Основными направлениями деятельности, при реализации которых целесообразно использование методов проектного управления, являются:

• –    строительство;

• –    реконструкция;

• –    разработка новой продукции/технологии;

• –    развитие социальной сферы;

• –    развитие информационных технологий;

• –    совершенствование методов управления;

• – энергосбережение;

  – инновационное развитие.

Для достижений стратегических целей развития отрасли и предприятия необходимо реализовывать «правильные» проекты, то есть управлять эффективным портфелем проектов. Существующие подходы поддержки принятия решений по отбору проектов в портфель ориентированы на различные проблемы, имеют свои преимущества и недостатки. Кроме того, каждое предприятие обладает своими особенностями, что затрудняет выбор подходящей методологии.

Рассмотрим существующие математические модели формирования портфеля проектов и оценим возможность их применения для решения обозначенных ранее проблем предприятий машиностроительной отрасли.

Для оценки возьмем выборку из следующих восьми проектов и присвоим им следующие порядковые номера:

• 1.    Создание единого диспетчерского центра электроснабжения.

• 2.    Обеспечение конкурентоспособной заготовкой основных производств.

• 3.    Организация производства новых моделей дорожной техники.

• 4.    Освоение производства новых моделей малогабаритной техники.

• 5.    Модернизация централизованной системы пневмоснабжения.

• 6.    Разработка строительной техники с уменьшенной массой кузова.

• 7.    Создание участка обработки крупного стального литья.

• 8.    Комплексная модернизация заготовительного и сварочного оборудования сборочного производства.

Рассмотрим простейшую модель ранжирования проектов на основе экономико-математического подхода к формированию портфеля, где используются финансовые показатели проектов. При использовании данной модели ранг проекта определяется по каждому из его показателей. Как правило, при ранжировании проектов используют следующие показатели:

– чистый дисконтированный доход ( NPV );

– внутренняя норма доходности ( IRR );

– период окупаемости ( PP );

– индекс окупаемости ( PI );

– рентабельность инвестиций ( Р ).

В таблице 1 представлены указанные показатели рассматриваемых проектов.

В качестве критерия оптимальности принятия решения принимается максимум комплексного показателя. Под максимальным значением комплексного показателя понимается такой на- бор показателей, в котором каждый из них достигает своего наилучшего значения (максимум или минимум в зависимости от своего качества).

Для получения значения комплексного показателя по результатам оценки проектов разрабатывается сравнительная таблица. При ее составлении одноименные показатели разных проектов ранжируются, причем наименьшая ранговая значимость присваивается проекту с наилучшим значением данного показателя. Обобщенная оценка каждого проекта осуществляется на основе суммирования ранговой значимости всех рассмотренных показателей эффективности. Лучшим по обобщенному критерию является проект с минимальной суммой рангов.

В таблице 2 отображена полученная ранговая значимость, а также суммарное ранговое значение.

Таким образом, наилучшим оказался проект № 7, наименьшие ранги получили проекты № 2 и № 8. Согласно данному подходу эти проекты следовало бы исключить из портфеля.

В основе принятия решений при использовании экономико-математических методов лежат

Таблица 1

Показатели проектов

№ проекта	NPV (млн руб.)	IRR (%)	PP (лет)	PI (%)	Р (%)
1	12,5	26,67	5,3	1,12	11,72
2	6,5	21	2,7	1,04	4,1
3	48	78,33	4,4	2,13	120,56
4	63	21,15	3,5	1,1	9,61
5	44	23,5	5,4	1,18	23,31
6	21	98,8	3,0	2,29	128,7
7	1 228	606,9	1,1	2,3	423,93
8	23	13,7	7,4	1,07	8

Примечание . Рассчитано авторами.

Таблица 2

Ранговая значимость проекта

№ проекта	NPV (тыс. руб.)	IRR (%)	PP (лет)	PI (%)	Р (%)	Сумма
1	8	4	7	6	6	31
2	9	8	3	9	9	38
3	3	3	6	3	3	18
4	2	7	5	7	7	28
5	4	6	8	5	5	28
6	7	2	4	2	2	17
7	1	1	1	1	1	5
8	6	9	9	8	8	40

Примечание. Рассчитано авторами.

количественные показатели проектов, что повышает объективность выбора, но не учитывает влияние качественных показателей проектов на достижение стратегических целей.

Учет качественных показателей осуществляется в экспертно-аналитических моделях. Простейшим подходом является применение опросных листов с последующим анализом экспертных оценок.

Проведем анализ рассмотренных ранее восьми проектов по степени их влияния на достижение стратегических целей предприятия. В таблице 3 приведены ранги восьми проектов, присвоенные им каждым из десяти экспертов в соответствии с собственным представлением экспертов о целесообразности включения проекта в стратегический план фирмы. Эксперт присваивал ранг 1 самому лучшему проекту, который обязательно надо реализовать, ранг 8 – наиболее сомнительному проекту, который реализовывать стоит лишь в последнюю очередь.

Представим полученные результаты расчетов по методу средних арифметических и методу медиан в таблице 4.

Сравнивая два метода в таблице 4, отметим, что общая тенденция ранжирования сохра- няется – наиболее приоритетными являются проекты 3, 4, 6, 7, наименее приоритетными – 1, 5, 8.

Подводя итог сравнению использования экономико-математического и экспертно-аналитического методов, следует отметить, что итоговые результаты данных методов могут различаться. Кроме того, методы представляют результаты субъективных оценок, не учитывают множество факторов, необходимых для получения достоверных данных. Оценка соответствию проектов стратегии в целом не является правильной, так как стратегия включает в себя цели, обладающие собственной приоритетностью. Проекты могут соответствовать всем целям стратегии, либо только одной, либо вообще не оказывать никакого влияния, что также необходимо учитывать в модели.

Одним из инструментов, позволяющих наглядно отображать количественные и качественные характеристики проектов, являются графические подходы. Наиболее популярны пузырьковые диаграммы, отображающие несколько параметров.

Используя результаты ранее проведенного анализа проектов, на рисунке 1 представлена

Таблица 3

Экспертные оценки стратегической значимости

№ эксперта	№ проекта
	1	2	3	4	5	6	7	8
1	7	5	2	1	8	3	4	6
2	7	5	1	3	8	4	2	6
3	6	1	4	5	8	7	2	3
4	5	6	2	2	8	4	1	7
5	7	8	6	4	3	2	5	1
6	8	5	3	4	2	6	1	7
7	7	6	3	2	5	1	4	8
8	8	5	2	3	7	1	4	6
9	8	6	2	3	5	1	4	7
10	7	5	1	2	8	3	4	6

Примечание . Составлено авторами на основе экспертных оценок.

Таблица 4

Сумма рангов

	1	2	3	4	5	6	7	8
Сумма рангов	70	52	26	29	62	32	31	57
Среднее арифметическое рангов	7	5,2	2,6	2,9	6,2	3,2	3,1	5,7
Итоговый ранг по среднему арифметическому	9	5	1	2	7	4	3	6
Медианы рангов	7	5	2	3	7,5	3	4	6
Итоговый ранг по медианам	7,5	5	1	2,5	9	2,5	4	6

Примечание . Рассчитано авторами.

пузырьковая диаграмма «стратегия – выгоды», где ось Х характеризует показатель соответствия проектов стратегическим целям, ось У отражает чистый дисконтированный доход NPV , диаметр соответствует периоду окупаемости проекта РР .

Однако, несмотря на наглядность и удобство применения графических методов, они не могут использоваться как основной инструмент управления портфелем. К тому же возрастание количества проектов ограничивает наглядность использования диаграмм.

Разработка модели формирования портфеля проектов предприятия машиностроительной отрасли

Для построения модели портфеля проектов необходимо учесть следующие факторы:

– определение входных величин проектов, существенных для данной организации, например, потребность в ресурсах, различные виды эффективности реализации проекта;

– определение синергетических параметров проектов, входящих в портфель, связи и зависимости между проектами, а также ожидаемое значение выходных величин проекта и их изменение в случае возникновения синергетического эффекта.

Учет указанных факторов затруднителен в случаях даже небольшого количества проектов. Поэтому необходимо разработать модель, позволяющую одновременно учитывать имеющиеся параметры, требуемые характеристики и ограничения как каждого проекта, так и всего портфеля в целом, составив при этом максимально эффективный портфель.

Определим характеристики математической модели формирования портфеля проектов.

Пусть P_j – проект, реализуемый в рамках организации и соответственно входящий в портфель проектов. Тогда для каждого проекта Р будем использовать следующие характеристики:

– минимальные требуемые инвестиции в проект ( W_i );

– чистый приведенный доход ( NPV_i );

– ресурсоемкость проекта ( HR_i );

– время реализации проекта ( T_i );

– «обязательность» проекта ( Ob_i ). В случае если Ob_i = 1, проект должен быть включен в портфель проектов, если Ob_i = 0, включение проекта не является обязательным;

– индекс соответствия стратегическим целям организации ( Str_i );

– риск проекта ( U ( w ));

– взаимозависимость проекта. Inf_i = { Inf_ij } – вектор влияния i -го проекта на j -й проект, где j ∈ 1, n ( n – количество проектов в портфеле);

– индекс улучшения качества бизнес-про-цессов в организации Bp_i ;

– индекс улучшения имиджа организации Im .

В итоге, определив параметры для потенциальных проектов, можем представить каждый проект как вектор значений:

P_j = { W_i , NPV_i , HR_i , T_i , Ob_i , Str_i , U ( w ), { Inf_ij }, Bp_i , Im }. (1)

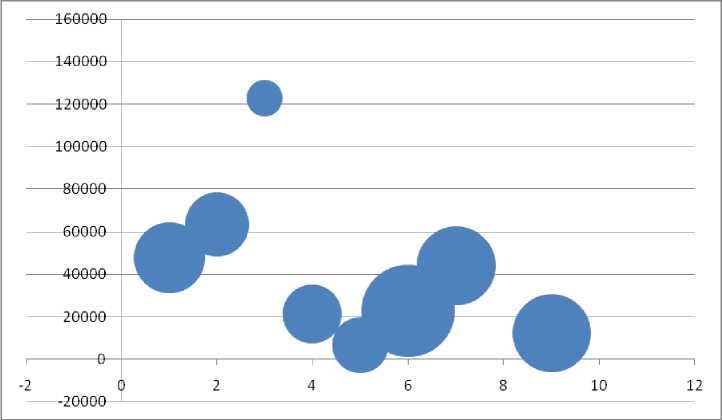
Рис. 1. Пузырьковая диаграмма

Примечание . Диаграмма построена авторами на основе данных таблицы 2.

Если проект не приносит измеримый доход, он должен иметь очень высокую степень соответствия стратегическим целям. Если проект приносит доход, то эта степень может быть ниже. Поэтому, при оценке привлекательности проектов целесообразно использовать как финансовые показатели, так и более широкий показатель – «полезность» проекта.

Полезность является субъективной оценкой, что усложняет ее формализацию. Можно выделить следующие факторы, определяющие полезность проекта:

– финансовый результат, измеряемый при помощи показателя NPV_i ;

– улучшение имиджа организации, измеряемое при помощи индекса Im (в баллах от 0 до 10);

– улучшение качества бизнес-процессов BP_i , измеряемое в баллах от 0 до 10.

Тогда функцию полезности можно представить следующим образом:

Y ( P ) = F ( Str , NPV_i , Im , BP_i ).              (2)

И измеряется она в условных единицах.

В результате получаем множество P ^* = { J_k } эффективных портфелей, которые обладают следующими свойствами:

P <  B

У HR, <  HR

= P

S

NPV ( J k J 6 P) >  NPV ( J k ,J k e P) .      (3)

_CT( J k ,J k 6 p ) <_CT( J k ,J k e p )

В результате моделирования должен быть получен портфель проектов, удовлетворяющий следующим условиям:

• 1.    Сумма минимальных инвестиций не превышает бюджет.

• 2.    Сумма по человеческим ресурсам не превышает ограничения.

• 3.    В максимальной степени соответствует стратегическим целям.

• 4.    Нет другого портфеля, у которого:

• –    выше NPV с тем же риском;

• –    ниже риск с тем же NPV .

Модель, удовлетворяющая указанным условиям, позволяет выбрать эффективный портфель проектов, который будет максимально способствовать достижению стратегических целей организации.

Далее, используя предложенную математическую модель, решим задачу формирова- ния портфеля для рассмотренных ранее восьми проектов.

Из исследуемой модели следует, что исходными данными для формирования эффективного портфеля являются:

• –    стратегические цели предприятия;

• –    бюджет на проектную деятельность предприятия;

• –    наличие свободных человеческих ресурсов.

На момент формирования портфеля проектов множество рассматриваемых проектов равно

P = J {1,1,1,1,1,1,1,1},                 (4)

каждый из проектов описывается десятью характеристиками, большая часть из которых определяется методом экспертных оценок.

Используя метод экспертных оценок, для каждого проекта определим значение полезности как функцию

Y ( P ) = F ( Str , NPV_i , Im , BP_i ).              (5)

Значения полезности задаются экспертами по балльной системе, и полезность принимает значения от 0 до 100.

Совокупный риск проекта определяем следующим образом: для каждого рискового j -го события ω ⁱ _j определяется вероятность наступления события P ( ω ⁱ _j ) и влияние, которое событие оказывает на полезность проекта U ( ω ⁱ _j ) . После определения вероятности всех элементарных событий и влияния их на результат проекта, получаем вероятностную величину совокупного риска проекта, характеризующего общее влияние рисков на проект. Условные риски рассматриваемых проектов представлены в таблице 5.

В таблице 6 приведены расчетные характеристики проектов.

Определим множество возможных портфелей проектов, с учетом того, что чем большее количество проектов включено в портфель, тем в большей степени портфель соответствует стратегическим целям организации. Для каждого портфеля из множества возможных портфелей определяется индекс соответствия стратегическим целям организации. В результате расчетов из возможных 33 портфелей были отобраны 8, у которых достигается наибольшее значение индекса соответствия стратегическим целям. Для определения эффективности портфелей проектов рассчитывается их полезность и совокупный риск. В таблице 7 представлены значения по ото-

Таблица 5

Риски проектов

Номер проекта	Риски
1	1.    Недостаточный уровень подготовки обслуживающего персонала 2.    Невозможность отключения потребителей по плановым работам 3.    Ошибки в оформлении отчетной документации
2	1.    Несоблюдение сроков поставок и монтажа 2.    Увеличение стоимости бюджета проекта из-за роста цен 3.    Отсутствие специалистов требуемой квалификации
3	1.    Изменения конъюнктуры рынка 2.    Недостижение заданных технико-экономических параметров 3.    Нарушение сроков изготовления опытных образцов
4	1.    Государственная поддержка конкурентов 2.    Нарушение сроков поставок 3.    Отсутствие поддержки руководства и прекращение финансирования проекта
5	1.    Недостаточная квалификационная подготовка обслуживающего персонала 2.    Несвоевременная поставка запасных частей 3.    Задержка монтажа и поставки
6	1.    Государственная поддержка конкурентов 2.    Сложность изготовления опытного образца в условиях действующего производства 3.    Снижение прогнозируемой величины сэкономленного металла
7	1.    Государственная поддержка конкурентов 2.    Рост цен на материалы и покупные изделия 3.    Ошибки в расчете бюджета проекта
8	1.    Увеличение цен на оборудование 2.    Увеличение тарифов на электроэнергию 3.    Увеличение сроков согласования и оформления договоров

Примечание. Составлено авторами.

Таблица 6

Характеристики проектов

Номер проекта	W	HR	Str	NPV	Im	Bp	Ob	T	Y ( P )	U ( w )
1	132	A	2	12,5	0	5	0	3	8	0,51
2	148	A	4	6,5	5	2	0	1,5	12	0,22
3	59	B	8	48	8	2	0	2,5	23	0,1
4	38	B	7	63	8	2	0	1	23	0,09
5	234	C	2	44	0	4	0	1,6	10	0,095
6	23	C	9	21	7	2	0	2	20	0,095
7	535	D	6	1228	2	3	0	1,5	23	0,09
8	359	D	6	23	1	2	0	3	11	0,095

Примечание. Составлено авторами.

бранным портфелям проектов, на рисунке 2 представлен график, где ось Х соответствует значениям риска портфеля, ось Y – ожидаемой полезности портфеля.

В результате расчетов были отобраны 3 портфеля проектов, каждый из которых показал наибольшую эффективность, это портфели 1, 7, 8. С точки зрения достижения стратегических целей организации предпочтительным является портфель проектов № 8, в который вошли все проекты из заданного списка, за исключением первого.

В итоге можно сделать вывод, что применение математических моделей является необходимым для деятельности современных предприятий. Модели позволят обеспечить связь между стратегическим и проектным управлением, обеспечат выделение ресурсов только на проекты, продвигающие предприятие к достижению стратегических целей.

Применение предложенной в работе математической модели формирования эффективных портфелей проектов, а также инструментарий на основе модели, позволит предприятиям обеспе-

Таблица 7

Совокупные значения для портфелей проектов

№	Состав портфеля	Бюджет	Индекс соответствия стратегическим целям	Ожидаемая полезность портфеля	Риск портфеля
1	{1,1,1,1,1,1,1,0}	1170	38	93,39	9,17
2	{1,1,1,1,1,1,0,1}	990	38	86,23	8,76
4	{1,1,1,1,0,1,1,1}	1300	42	92,56	9,89
7	{1,0,1,1,1,1,1,1}	1380	40	73,28	8,32
8	{0,1,1,1,1,1,1,1}	1400	42	86,37	8,59
9	{0,0,1,1,1,1,1,1}	1250	38	71,86	8,78
18	{0,1,1,1,0,1,1,1}	1160	40	63,99	8,78
23	{1,0,1,1,0,1,1,1}	1140	38	65,32	8,51

Примечание. Составлено авторами.

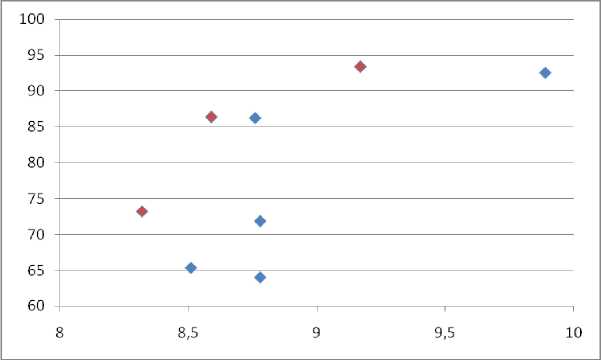
Рис. 2. Множество эффективных портфелей

Примечание. Построен авторами на основе данных таблицы 7.

чить достижение стратегических целей с минимальным риском.

По данным Международной Ассоциации Управления Проектами (IPMA) использование современной методологии и инструментария управления проектами, в том числе математических моделей, позволяет сэкономить порядка 20–30 % времени и около 15–20 % средств, затрачиваемых на осуществление проектов и портфелей проектов. Таким образом, использование математических моделей в управлении проектами является эффективным методом, позволяющим оперативно реагировать на изменения внешних требований и достигать стратегических целей с минимальными затратами ресурсов.