Формирование эталонных волновых фронтов с использованием дифракционных оптических элементов

Традиционно расчет оптических элементов -формирователей волнового фронта - проводился методами цифровой голографии или методами лучевой оптики[1]. Однако, оптический элемент, созданный голографическим способом, работает в некотором порядке дифракции, что приводит к низкой энергетической эффективности. Лучевой же подход не учитывает эффекта дифракции света в свободном пространстве, что приводит к искаженному формированию требуемого распределения фазы. В данной работе рассматривается итеративный алгоритм для расчета формирователей волновых фронтов, работающий в рамках дифракционной оптики, и, следовательно, свободный от перечисленных недостатков. Этот алгоритм является модификацией известного алгоритма Герчберга-Секстона (ГС), использовавшегося для расчета дифракционных элементов, формирующих заданное распределение интенсивности, - киноформов [2-4]. Результаты численных экспериментов подтвердили эффективность предложенного метода.

Обсуждается, также, модификация алгоритма ГС для расчета амплитудных линз. Приведенные численные результаты демонстрируют хорошую работоспособность таких оптических элементов.

где у ₀( 5 , п ) - требуемое распределение фазы в плоскости, находящейся на расстоянии z от элемента, A ( x , у ) - амплитуда освещающего пучка (для плоской волны A ( x , у )=1), ф ₀( x , у ) - искомая фаза.

Алгоритм решения уравнения (2) следующий [5]. Начальное приближение искомой фазы ф ₀( x , у ) выбирается случайным. От функции A ( x , у ) е ' ^ф ° ⁽ x ^{, у} ) вычисляется преобразование Френеля. Полученная функция F_n ( 5 , п ), где n - номер итерации, заменяется на функцию F_n ( 5 , п ) по правилу:

F n '(5, П ) = | F „ ( 5 , П )| e" " ^{0 5п} )

От функции F_n ( 5 , п ) вычисляется преобразование Френеля и полученная

обратное функция

f_n ( x , у ) в плоскости элемента заменяется на функцию f_n ' ( x , у ) по правилу:

fn'( x, У ) =

A ( x , у ) I ^{fn (} x , ^у ) , ( x , у Fⁿ

I f n ⁽ x , у )| ^V ' (4)

Алгоритм расчета фазового ДОЭ

Если плоскость наблюдения ( 5 , п ) расположена в зоне дифракции Френеля, то комплексные амплитуды света в плоскости оптического элемента f ( x , у ) и в плоскости наблюдения F ( 5 , п ) связаны преобразованием Френеля:

[        0, (x, у )<й

Сходимость этого процесса контролируется по среднеквадратичному отклонению:

5 =

от

J J[w0 (5,п)-Wn (5,п)]2 d5dn

-от

_ 1/

/2

где

F ( 5 , п ) = k JJ f ( x , у ) H ( x - 5 , у - п ) dxdy ,    (1)

z n

от

J J[w0 (5,п)]2 d5dп

-от

у ₀ и y _n - заданная и рассчитанная на n -й итерации фазы светового поля на расстоянии z .

А ik 2 2       2.

H ^{( x} , у ) = ^exp —⁽ x + у ) 2 z

- функция оптического отклика свободного пространства, k=2 n / X - волновое число света с длиной волны X , z - расстояние между плоскостями, Q -форма апертуры оптического элемента.

Для расчета фазового формирователя волнового фронта необходимо решить методом последовательных приближений нелинейное интегральное уравнение скалярной дифракции света:

У 0(5, п) = arg {JJ A(x, у) еф 0< x,У) Q хH(x - 5, у - п)dxdy}

Результаты численного эксперимента

Алгоритм (3)-(4) использовался для расчета фазовых оптических элементов, формирующих заданные распределения фазы полиномиального типа на некотором расстоянии. Были выбраны следующие параметры расчета: число отсчетов 128x128, радиус круглой диафрагмы Q равен 0.3мм, дискретность по переменным (x,y) и ( ^ , р ) равна 0.01 mm , k = 10 ⁴ mm ¹ , z ₀=20 mm - расстояние до плоскости наблюдения. Амплитуда пучка, освещающего элемент, была гауссовой:

,

A o ^{( x} , У ) = exp -

2       2

x + у w

Количество итераций равно 10. Дальнейшее увеличение числа итераций не приводило к замет- ному изменению результатов.

На Рис.1 показаны результаты расчета для случая формирования волнового фронта следующего вида:

У 00^, П ) = а

a)

, а = 300 mm

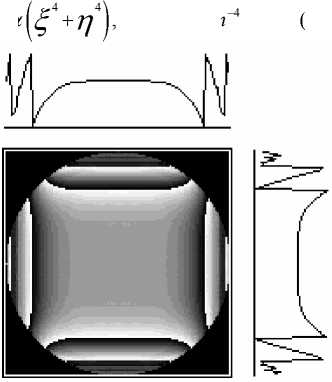
На рис. 1 показаны: фаза ф (x,y) оптического элемента (а), ее центральные сечения по осям x и y ; и фаза, сформированная на расстоянии z 0 (б), ее центральные сечения по осям ^ и п (сплошная линия на рис.1б - рассчитанная фаза, пунктирная линия - заданная фаза (5)). Отличие рассчитанной фазы (рис.1б) от заданной составило 0,1%.

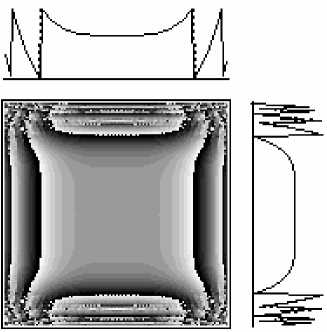
Рис. 1. Формирование волнового фронта: а) - распределение фазы на элементе, освещаемом гауссовым пучком; б) - распределение фазы на расстоянии z o .

Затем дополнительно была введена на каждом шаге операция квантования функции распределения фазы по M уровням значений фазы: Затем дополнительно была введена на каждом шаге операция квантования функции распределения фазы по M уровням значений фазы:

2 n m

^$ k ⁽ x-y ) = MT¹

2nm      2п( m +1)

- ^ф к - —47—

Mk    M

где k - номер итерации.

На рис. 2 и рис. 3 приведены результаты квантования для предыдущего случая формирования волнового фронта у ₀ ( £ , п ) по 10 и 5 уровням фазы соответственно.

При этом отличие рассчитанной фазы от заданной составило в среднем 7,7% для рис.2 и 15,7% для рис.3.

к = 1, N , m = 0, M - 1,

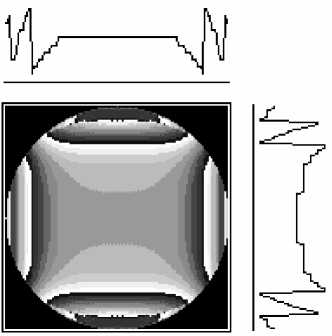
Рис. 2. Формирование волнового фронта с квантованием фазы по 10 уровням. а)- распределение фазы на

б)

элементе, освещаемом гауссовым пучком

Приведенные результаты говорят о том, что, применяя предложенный алгоритм, за небольшое число итераций удается рассчитать фазовые оптические элементы, которые на некотором расстоянии формируют волновые фронты типа

у ( ^ , П ) = +а ( ^ ^к ± П ) ,

; б)-распределение фазы на расстоянии z₀ отличающиеся от заданных не более, чем на 7-8% при не менее, чем 10-ти уровнях квантования.

Амплитудные линзы

Рассмотрим еще один вариант модификации алгоритма ГС, позволяющий решить задачу расчета амплитудных линз. В данном случае методом по- следовательных приближений решается интегральное уравнение вида:

I ( 5 , п ) = ^П ⁵ ( x , У ) H ( x - 5 , У - п ) dxdy (6) 2 n z "

n

а)

Решение уравнения (6) ищется из условия минимизации функционала:

- ,                                           2

M = JJ W ( 5 , п ) [ 44 - F ( 5 , п )| ] d ^ d n +

-да да

+а ² J J \F ( 5 , п )|² d 5 d n

-да

где 10 = I (50, По) - пиковое значение интенсивности в точке (50,п0), W(5,п) - весовая апертурная функ- ция:

W ( 5 , п )

[ 1, ( 5 , п ) е S [ 0, ( 5 , п ) ^ S ^,

S - малая область вблизи точки, а - постоянная, регулирующая уровень энергии рассеянного света. Первое слагаемое в (7) показывает отклонение рассчитанного поля от пика интенсивности в точке (50, п0). Максимальная дифракционная эффектив- ность достигается при условии примерного равенства энергии шума и сигнала:

да

1 0 ~ а ² JJ | F ( 5 , п )|² d 5 d n                    (8)

-да

Алгоритм минимизации функционала (7) аналогичен алгоритму ГС (3)-(4), но вместо замены (3) используется замена:

F© (5, п ) = (44W (5, п) + а F (5, п )|) |F51, (9)

а вместо замены (4) используется замена f'(x, У ) =

If(x,У)|, (x,У^О О, (x,У)^Q

где I ( 5 , п ) - требуемое распределение интенсивности на расстоянии z от амплитудного транспаранта, 5 ( x , y ) - искомое распределение амплитуды транспаранта.

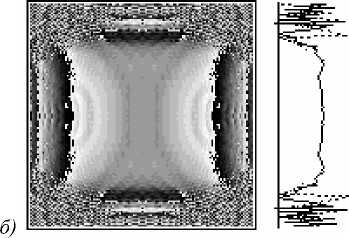
Рис. 3. Формирование волнового фронта с квантованием фазы по 5-ти уровням. а)-распределение фазы на элементе, освещаемом гауссовым пучком; б)-распределение фазы на расстоянии z 0

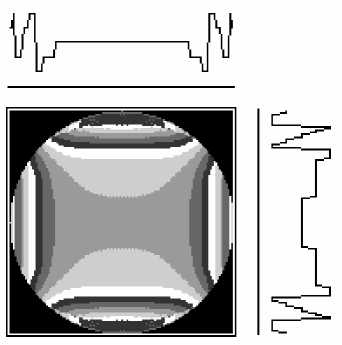
На рисунке 4 представлены результаты численного эксперимента, моделировавшего работу амплитудной линзы, рассчитанной при помощи алгоритма (9)-(10). Рис. 4(а) демонстрирует амплитудный элемент, освещавшийся плоским пучком и его центральное сечение, а рис. 4(б) - распределение интенсивности на расстоянии z ₀=160 mm . Диаметр линзы равен 3 mm , волновое число k = 10 ⁴ mm "1 . Число итераций равно 15. Дифракционная эффективность полученной линзы составила 18,2%.

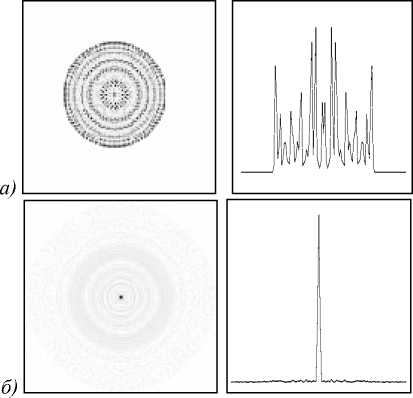
Рис. 4. Расчет амплитудной линзы: а) рассчитанный элемент и его центральное сечение; б)распределение интенсивности на расстоянии z 0 .

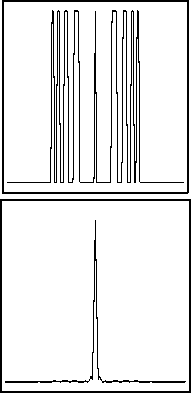
На рисунке 5 приведены результаты работы амплитудной зонной пластинки Френеля с параметрами, аналогичными параметрам рассчитанной линзы. Рис. 5(а) демонстрирует распределение амплитудных зон на пластинке, а рис. 5(б) - распределение интенсивности светового поля на расстоянии z0 и его центральное сечение. Дифракционная эффективность зонной пластинки составила 20,9%, но ширина центрального пика интенсивности была несколько больше, чем для амплитудного элемента, рассчитанного итеративным методом.

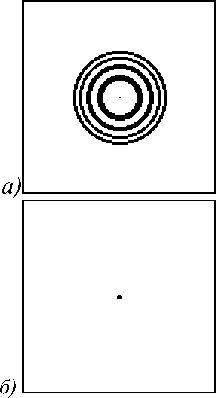
Рис. 5. Амплитудная зонная пластинка: а) - амплитудное пропускание зонной пластинки; б) -распределение интенсивности на расстоянии z0 и его центральное сечение.

Заключение

Таким образом, в данной работе были представлены итеративные алгоритмы расчета дифракционных оптических элементов, формирующих заданные распределения фазы когерентного светового поля, и амплитудных линз, основанные на модификациях алгоритма Герчберга - Секстона. Приведены численные результаты, демонстрирующие возможность успешного применения предложенных алгоритмов.