Формирование кластерных агрегатов с пентагональной симметрией в пластически деформированных образцах Ni51Ti49

Введение. Известно [1], что сплавы системы «никель– титан», обладающие эффектом памяти формы, широко применяются при изготовлении разнообразных изделий ракетно-космической и авиационной техники. В связи с этим актуальным является исследование особенностей структурно-фазовых превращений в сплавах с эффектом памяти формы Ni 51 Ti 49 , происходящих при пластических деформациях.

Многие исследователи [2–5] наблюдали возникновение монокристаллов линзовидной формы, которые содержали большое количество изгибных экстинкци-онных контуров, свидетельствующих о значительной кривизне кристаллической решетки, возникающей из-за концентрации напряжений в локализованных областях [6].

В нашей работе [7] в образцах сплава Ni51Ti49, подвергнутых растяжению, обнаружены линзовидные кристаллы, отличающиеся составом и структурой от структуры матричного сплава. Сделанные оценки внутренних напряжений показывают, что в зонах локализации деформации могут создаваться напряжения, превышающие предел прочности для всего материала [7].

В работе была показана возможность появления ГЦК-решетки в массивных образцах никелида титана после растяжения [8]. На основании расшифровки дифракционных картин нами показано, что процесс мартенситного превращения структуры B2 может проходить по схеме Курдюмова–Закса. Описание превращений при помощи моделей относительных смещений плоских сеток затруднено в связи с различными обозначениями атомных плоскостей и векторов прямой и обратной решеток для структур с различной симметрией.

Одной из активно развивающихся концепций структурообразования является концепция кластерного

моделирования трехмерных структур. В этом методе полиморфное мартенситное превращение описывается не как относительное смещение плоских атомных сеток, а как реконструкция трехмерных координационных полиэдров, составляющих кристаллические структуры фаз-партнеров по фазовому превращению с сохранением их связности [9–12]. Метод основан на представлении каждого структурного состояния в виде комбинации элементарных кристаллических кластеров. Кластер – это система атомов, (частиц) свойства которой зависит от их числа [13]. Кластеры собираются на основе кристаллических модулей и/или симплексов. Кристаллический модуль – однозначно выделенная только по химическим связям в структуре кристаллов пустота в виде полиэдра, заполняющего при параллельном переносе все пространство. Модуль может быть образован несколькими симплексами. Симплекс – полиэдр, образованный атомами структуры, лежащими на поверхности пустой сферы, ребрами которого являются кратчайшие межатомные расстояния (химические связи) [10]. Таким образом, кластерные агрегаты – это комбинация кластеров, порожденных симплексами и/или модулями различных кристаллических решеток.

Нам удалось показать возможность существования фазы с ГЦК-решеткой в никелиде титана [14] при помощи кластерного моделирования. С помощью кластерного моделирования предложена схема мартенситных превращений в никелиде титана из структуры В2 (ОЦК-решетка) в структуру В19´ (ГПУ-решетка) через промежуточную фазу с ГЦК-решеткой.

В работе [15] предложена модель кристаллической структуры мартенситной R -фазы в системе Ni–Ti, основанная на кластерном подходе: ромбододекаэдр исходной ОЦК-структуры превращается в конечный кубооктаэдр через промежуточные конфигурации

кластера особой фазы и икосаэдра. Автор [16] допускает, что наблюдаемые структуры с пентагональной симметрией на самом деле периодические и обладают не икосаэдрической, а близкой к икосаэдрической кубической симметрией. В [17] показано, что повышение точечной симметрии кристалла может быть вызвано несоразмерной деформацией исходной периодической структуры, обладающей более низкой точечной симметрией. Несоразмерная деформация приводит к атомным смещениям, в работах В. Г. Пушина, например [18], показана возможность значительных атомных смещений, превышающих несколько десятых долей ангстрема, при мартенситных превращениях в никелиде титана.

Проблема структурообразования в никелиде титана при пластической деформации является предметом широких дискуссий и нуждается в дополнительных исследованиях.

Цель работы – исследование микроструктуры линзовидных кристаллов, возникающих при пластической деформации образцов Ni 51 Ti 49 .

Задачи работы:

• 1.    Методами электронной микроскопии исследовать микроструктуру утоненных массивных образцов сплава Ni₅₁Ti₄₉, подвергнутых растягивающей нагрузке на испытательной машине.

• 2.    Методами дифракции электронов исследовать структурно-фазовые превращения при формировании линзовидных кристаллов в области шейки растянутого образца.

• 3.    Объяснить с помощью представлений о кристаллических модулях возможности формирования в зонах локализации деформации кластерных агрегатов с пентагональной симметрией.

Образцы и методы. Термически обработанные образцы сплава Ni₅₁Ti₄₉ подвергались статическому растяжению до разрыва на испытательной машине WDW-5E. Для исследования образцов методами просвечивающей электронной микроскопии (ПЭМ) на микроскопах Hitachi 7700 и JEOL-2100 подготавливали

образцы с помощью ионного травления на установке PIPS (Gatan). Подробнее методика изложена в [7].

Экспериментальные результаты. На рис. 1. приведено электронно-микроскопическое изображение утоненного образца Ni 51 Ti 49 , растянутого до разрыва в области шейки. Наблюдается линзовидный кристалл с многочисленными экстинкционными контурами внутри [7].

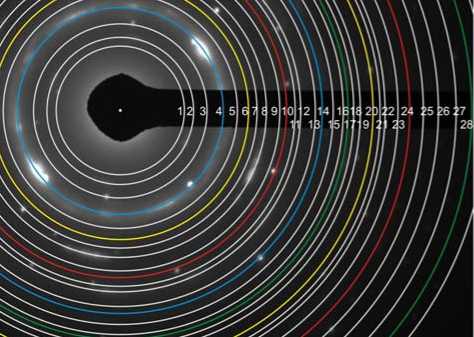
Картина дифракции электронов, полученная от линзовидного кристалла, показанного на рис. 1, приведена на рис. 2. Особенностью дифракционной картины является наличие пентагональной симметрии, о которой свидетельствуют десять рефлексов, расположенных с шагом 36° на наиболее интенсивном дифракционном кольце (рис. 2, а ). Схема расшифровки показана на рис. 2, б , а данные сведены в таблицу.

При составлении таблицы исходили из того, что параметр решетки В2 а = 3,01 Å [19]. Значение d ₁₁₀ ячейки В2, равной d ₁₁₀ = 3,01/√2 = 2,13 Å [20], присвоили линии 4 (см. рис. 2, а , таблицу). Исходя из этой величины, были получены остальные линии ОЦК-решетки В2, соответствующие исходной матрице, окружающей линзовидный кристалл (см. таблицу).

В нашей работе [14] было показано, что при мартенситном переходе в никелиде титана возможно формирование фазы с ГЦК-решеткой, причем рефлекс [110] ОЦК близок к рефлексу [111] ГЦК . Исходя из этой предпосылки, мы присвоили индекс [111] ГЦК линии 4 и, сделав необходимые расчеты, выявили рефлексы ГЦК-решетки (см. таблицу) с параметром а = 3,68 Å. Оставшиеся линии расшифровывались как индексы примитивной кубической решетки с параметром а = 2,13 Å, причем индекс [100] ПК оказался также лежащим на линии 4 (основном дифракционном кольце).

Обсуждение результатов. У. Пирсон [9] описывает структуру ОЦК-решетки (рис. 3) как систему, состоящую из 6 неправильных октаэдров (рис. 3, а ). Согласно [10] ГЦК-решетка может быть представлена как комбинация одного правильного октаэдра, окруженного правильными тетраэдрами, связанными общими треугольными гранями (рис. 3, б ).

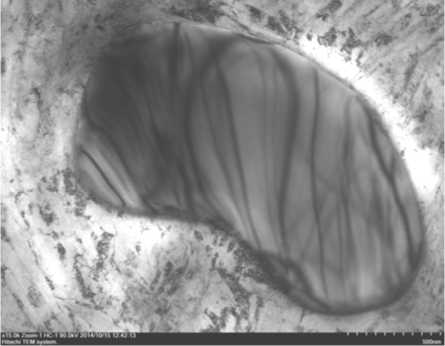
Рис. 1. ПЭМ-изображение линзовидного кристалла, выросшего в зоне локализации напряжений деформированного образца Ni51Ti49

Fig. 1. TEM image of lens-shaped crystal grown in the zone of electric porential location of deformed sample Ni51Ti49

а

Рис. 2. Дифракционная картина, полученная от линзовидного кристалла, представленного на рис. 1: а – десять рефлексов, расположенных с шагом 36° на дифракционном кольце с наибольшей интенсивностью; б – схема расшифровки дифракционной картины, представленная в таблице

б

Fig. 2. Diffraction pattern received from lens-shaped crystal, shown on fig. 1:

a – ten reflexes situated in increments of 36° on the diffraction circle with the utmost intensity; b – scheme of decipher of diffraction pattern shown on table

Результаты расшифровки дифракционной картины, приведенной на рис. 2

Номер линии	Межплоскостное расстояние d , Å	Объемно-центрированная кубическая решетка	Гранецентрированная кубическая решетка	Примитивная кубическая решетка
1	3,44	½ ½ ½ *(+0,04)
2	2,99	100* (+0,02)
3	2,53		110*(+0,07)	½ ½ ½*(–0,07)
4	2,13	110	111	100(–0,01)
5	1,86		200(–0,02)
6	1,71	111*(+0,03)
7	1,63		210*(–0,02)
8	1,50	200(+0,01)	211*(0,00)	110(+0,01)
9	1,37	210*(–0,02)
10	1,31		220(+0,01)
11	1,25			111(–0,02)
12	1,22	211(+0,01)	221*(+0,01)
13	1,12		311(–0,01)
14	1,09		222(–0,03)	200(–0,02)
15	1,03	220(+0,03)
16	0,98	300*(+0,02)
17	0,96			210(–0,01)
18	0,94	310(+0,01)
19	0,91		400(+0,01)
20	0,87			211(0,00)
21	0,84	222(+0,03)	331(0,00)
22	0,83		420(–0,01)

Окончание таблицы

Номер линии	Межплоскостное расстояние d , Å	Объемно-центрированная кубическая решетка	Гранецентрированная кубическая решетка	Примитивная кубическая решетка
23	0,79	321(+0,01)
24	0,75	400(0,00)	422(0,00)	220(0,00)
25	0,71	411(0,00)	511(0,00)	221(0,00)
26	0,68	420(–0,01)		310(–0,01)
27	0,65	332(–0,01)	440(0,00)	311(+0,01)
28	0,62	422(–0,01)	531(0,00)
29	0,60	511*(–0,02)	442(+0,01)