Формирование кластеров в процессе колонизации ареала двухвозрастной популяции

Как известно, многие популяции характеризуются неравномерным или мозаичным распределением по ареалу, и существует множество гипотез такого распределения. Часто его связывают с географическими особенностями ареала. Например, естественные барьеры типа гор, рек и т.п. определяют то, куда особи популяции в принципе способны распространиться, т.е. предполагается, что особи достаточно подвижны и за непродолжительное время (за небольшое число поколений) способны перераспределиться по ареалу [5, 6]. Кроме того, пространственная приуроченность популяции к тому или иному местообитанию может быть связана с распределением по территории пищевого ресурса, необходимого для жизнедеятельности. В результате особи в большом числе локализуются на территориях с богатыми ресурсами, а на бедных территориях численность оказывается минимальной. С другой стороны, существует гипотеза о «внутренних» механизмах формирования неоднородного распределения, связанного с конкурентными взаимодействиями особей между собой или другими видами. Например, особи разных стадий развития могут отличаться своей подвижностью, конкурировать между собой или представителями другого вида. В результате, если существует несколько местообитаний, то особи мигрируют между ними вследствие этих взаимодействий или особенностей жизненного цикла, т.е. происходит вытеснение представителя той или иной стадии развития на другую территорию из-за конкурентных взаимоотношений. Взаимодействие же с другими видами может выражаться, например, в том, что происходит миграция хищника за жертвой (таксис) [3, 16].

Одним из методов изучения неравномерного распределения является математическое моделирование. В данной работе исследуется модель пространственной динамики структурированных популяций с дискретным временем и пространством, которая представляет собой систему или решетку связанных двумерных отображений (двух рекуррентных уравнений) [15]. Рассматривается популяция с двумя возрастными классами – младшим и старшим. Предполагается, что существует несколько местообитаний с проживающими там локальными популяциями с возрастной структурой, между которыми наблюдаются сезонные миграции особей старшего поколения [9, 10].

В рамках данной модели рассматриваются механизмы синхронизации (в том числе кластерной) и формирования неоднородного распределения в процессе расселения или колонизации одномерного линейного ареала (кольца) из единственной субпопуляции с ненулевой численностью. Подобная форма ареала возникает для популяций животных, у которых ареал вытянут вдоль какого-либо природного объекта, например, русла реки, долинного комплекса, берега острова или озера, склона горы, границы между лесом и лугом [2, 4, 7]. Заселение ареала из единственной локальной популяции наблюдается, например, в случае катастрофического уничтожения популяции почти на всем ареале и последующего его восстановления из единственной выжившей популяции. Кроме того, такая ситуация характерна для новых и пионерских для данной территории видов, заселяющих территорию [11].

Вместе с тем вопросы расселения и формирования неравномерного распределения в данной модели тесно связаны с вопросами пространственной синхронизации и десинхронизации, т.е. тем, как особенности динамики популяции на удаленных территориях связаны между собой, и тем, как это влияет на формируемые пространственные структуры. Данный вопрос, в частности, предполагает, что динамика популяции носит колебательный характер, т.е. численность не постоянна и периодически или апериодически изменяется во времени, или сложным образом флуктуирует. В этой связи интересны разнообразные нелинейные феномены, характерные для связанных колебательных элементов. Это, например, такие явления, как синхронизация, в том числе хаотическая и кластерная, пространственно-временной хаос, пространственно-временная перемежаемость, химеры и др. [1, 12–14]. Данная работа посвящена исследованию таких явлений в структурированных популяциях методами математического моделирования и теории синхронизации.

Модель пространственной динамики популяции с возрастной структурой В работе исследуется следующая математическая модель с дискретным временем и пространством, предложенная в [10]:

( i )             ( i )                   ( i )        ( i )

x n + 1 = a y n exp — ^X^n — y n )

i + P

(i)          (i)        (i) m v          (j)       (i) , yn +1  s xn + v n +     ^\yn   yn )

• ^{2 P} j = i - P

( i = 1,2, _ , N ). (1) где x_n ^{( i )} и y_n ^{( i )} – численности младшего и старшего возрастных классов в i -м локальном участке в n -й сезон, a – репродуктивный потенциал или максимальный коэффициент рождаемости, s и v – коэффициенты выживаемости соответствующих возрастных групп, параметр N определяет степень участия младшего возрастного класса в плотностно-зависимой регуляции рождаемости [9, 10]. Рассматривался ареал в форме одномерного кольца, а это значит, что имеется N связанных местообитаний с проживающими там субпопуляциями.

Связь в системе (1) представляет собой нелокальную миграцию старших особей, а это означает, что доля взрослых, равная величине m, один раз в сезон покидает свое родное местообитание и мигрирует не только на соседние участки, но и на P удаленных от него территорий, соответственно слева и справа от его родного участка. Если P =1, то связь локальная и связанными оказываются только соседние субпопуляции. Например, первая связана со 2-й и с N- й. Если P= 2, то первая популяция связана со 2-й и 3-й, а также N- й и N- 1-й, и т.д. В этом смысле расстояние между субпопуляциями определяется их расположением на кольцевом ареале, т.е. номером i , а также радиусом связи, равным величине P . Такое модельное описание миграции предполагает, что особи явно отличаются своей мобильностью (при P> 1), т.е. одна их часть способна мигрировать лишь локально (в соседние местообитания с номерами i ± 1 ), а другая часть перемещается на более отдаленные территории (с номерами i ± 2 , i ± 3 и т.д., но не далее чем i ± P , где P <  N /2).

Надо заметить, что в отсутствии связи (т.е. m = 0) каждая локальная популяция, которая описывается этой моделью, демонстрирует весьма сложное поведение [9]. Например, в зависимости от соотношений демографических параметров системы (1) возможна потеря устойчивости по двум сценариям. Во-первых, через образование предельной инвариантной кривой, во-вторых, через удвоение периода, и, соответственно, при определенных популяционных параметрах формируются квазипериодические, а при других хаотические режимы динамики численности. Кроме того, в этом случае наблюдается мультистабильность, т.е. в зависимости от начальных численностей взрослых y ₀ и детей x ₀ формируются принципиально разные динамические режимы, например, колебания численностей с разными периодами. В этой связи особый интерес вызывает то, к чему приводит миграционная связь между популяциями со столь сложным динамическим поведением.

Синхронизация, кластеризация, химеры в ходе колонизации

Основные феномены, которые возникают в модели (1), связаны с явлением синхронизации динамики соседних и удаленных субпопуляций [8–10]. Если все субпопуляции оказываются синхронными, т.е. их динамика максимально близка друг к другу (совпадают периоды, близки фазы и амплитуды колебаний), то говорят о полной синхронизации. Если же можно выделить две или бо- лее группы синхронных элементов, то говорят о кластерной синхронизации или, просто, кластеризации. Кроме того, возможна ситуация, когда среди синхронных элементов могут начать появляться одиночные несинхронные элементы, которые выбиваются из общего ритма колебаний. В этом случае говорят о химерных состояниях или, для простоты, о химерах [13]. И, наконец, все элементы могут быть несинхронными друг другу, и тогда говорят о несинхронном или о некогерентном поведении. Кроме того, несинхронные элементы сами могут образовать кластер, о котором можно говорить, если одновременно с ним существует кластер с синхронной динамикой.

Рассмотрим особенности формирования неоднородного пространственного распределения по ареалу при следующих начальных условиях:

• (1)                (100)        (1)                (4 9)        (51)

x 0    ”• x 0       y 0    ”• y 0       y 0

которые приводят к задаче заселения или колонизации изначально пустого ареала. Здесь существенно, что ареал имеет кольцевую форму и поэтому не столь важно, какую именно ненулевую субпопуляцию рассматривать.

В этом случае пространственно-временную динамику системы (1) при начальных условиях (2) удобно представить тремя способами, показанными на рис. 1, где у 05⁰⁾ = 1.6 . Выбранные популяционные параметры a , s , v и ρ в данном случае соответствуют устойчивым колебаниям периода 2 (2-цикл) локальной популяции.

На рис. 1, во-первых, приведены профили (снизу) асимптотических пространственно-временных режимов, на которых по оси абсцисс отложен номер субпопуляции i , а по оси ординат значения переменной y за достаточно большой период времени. В результате численность i -й субпопуляции в n -й сезон, равная у Пi ) ( i = 1,2, ^ , N ),

= y 01⁰⁰) = 0, y 0^{5 0)} >  0,              (2)

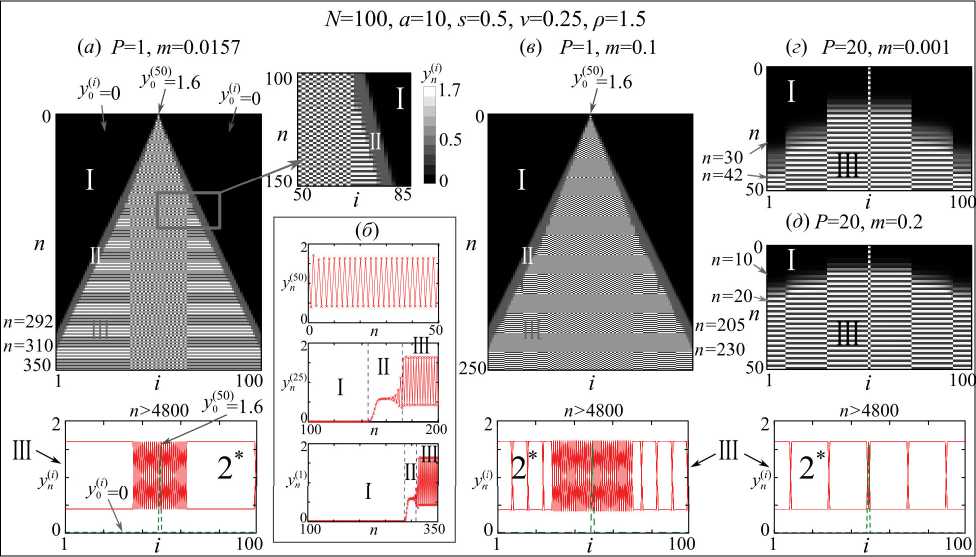
Рис. 1. Кластеры и химеры, возникающие в процессе колонизации кольцевого ареала, состоящего из 100 местообитаний, из единственной ненулевой субпопуляции с численностью y ₀ ^{(5 0)} при различных параметрах связи, а также профили (снизу). I–III – этапы колонизации, число – регистрируемый период колебаний, 2^* – химера

Fig. 1. Clusters and chimeras arising at colonization of the ring-shaped area, consisted of 100 habitats, of a single non-zero subpopulation with the number equal to y ₀ ^{(5 0)} , at various couple parameters; and profiles, as well (below). I–III – the stages of colonization, figure – a detected period of fluctuation, 2^* – chimera

соответствует одной точке на профиле, соединив которые, для всех N субпопуляций получаем одну из линий профилей для n -го сезона. Вычислив достаточное число итераций ( n = 0,1,2,..,5000) уравнений (1) и отбросив большую их часть от начала (оставив n = 4800,4801,..,5000), получаем несколько линий, изображенных на профилях, которые полностью характеризуют асимптотическую пространственную динамику. Например, часть этих линий сливается, что, с одной стороны, говорит о том, что имеет место точная повторяемость значений численностей через определенное число итераций (проверено численно с точностью 10^-9), а, с другой, по их числу легко судить о периоде колебаний (с точностью 10^-9), который отмечен для каждого профиля. Если такой повторяемости нет, то имеет место нерегулярная или хаотическая динамика во времени. Кроме того, видно, что некоторые линии пересекаются, а это значит, что когда численность субпопуляций в одной группе (кластере) достигает максимальных значений, другие субпопуляции демонстрируют минимальные значения, и наоборот, т.е. их динамика оказывается несинхронной (не совпадают фазы). Таким образом, по виду профилей легко судить о наличии кластеров синхронных субпопуляций, у которых полностью совпадает фаза и период колебаний.

Во-вторых, на рис. 1 (сверху) показана динамика субпопуляций во времени, где по оси абсцисс отложен номер субпопуляции i , по оси ординат дискретное время n сверху вниз, а значению численностей соответствует яркость точек на пересечении номера i и времени n . Черной точке соответствует нулевая численность субпопуляций, белой – максимальная, а серой – некоторые промежуточные значения (легенда показана на выноске в рис. 1 а ). Такое представление, в отличие от профилей асимптотических пространственно-временных режимов, позволяет проследить динамику с первых итераций модельных уравнений и в деталях изучить процесс колонизации.

Наконец, динамика отдельных субпопуляций на рис. 1б представлена в виде графиков численностей, т.е. показана зависимость y(i) от дис-n кретного времени n для фиксированных номеров местообитаний i.

Численные эксперименты позволяют заключить, что модельный процесс расселения состоит из трех этапов, обозначенных на рис. 1 латинскими цифрами I, II и III.

• (I)    На первом этапе происходит начальное заселение ареала из единственной непустой

субпопуляции с выбранным в соотношениях (2) номером i = 50 ( y ₀ ⁽⁵⁰⁾ >  0 ). На рис. 1 а это начальное состояние расположено на вершине полосатого треугольника, а справа на рис.1 б показана динамика численности именно этой субпопуляции, которая представлена колебаниями с периодом 2 практически с самых первых итераций модельных уравнений (рис. 1 б ). Благодаря миграции пустые местообитания постепенно заполняются мигрантами, и чем дальше местообитание расположено от начального, тем позже оно заполняется. Следует ожидать, что это произойдет ровно через N /2 сезонов. Однако этого не происходит, что связано с несколькими обстоятельствами.

Во-первых, помимо механического движения по типу диффузии (миграционный член в системе (1)), в популяции присутствует смертность особей старшего возрастного класса (член vy ), в том числе вновь прибывших, а также выживаемость неполовозрелых особей (член sx ). В результате прирост численности на колонизируемых территориях оказывается значительно ниже того, что имел бы место при простой диффузии и отсутствии смертности ( s= 1, v= 1). Таким образом, за N /2 сезонов «края» ареала никто не достигает (модельная численность меньше10^–32). Во-вторых, модельные темпы воспроизводства на колонизируемых территориях оказываются значительно ниже темпов смертности и миграции на сопредельные территории, что, вероятно, связано с небольшими численностями мигрантов и/или с низким репродуктивным потенциалом. В результате, например, 24-ю субпопуляцию мигранты достигают примерно через 150 сезонов, а 1-ю лишь через 292 сезона (рис. 1 б ). В данном случае мы считаем, что местообитание колонизировано, если плотность населения там значительно больше нуля (больше 10^–6). Графически этот этап на рис. 1 а изображен в виде двух черных треугольников, где численность субпопуляций примерно равна нулю (меньше 10^–6).

• (II)    На втором этапе, после того как численность начинает превышать некоторое критическое значение (более 10^–6) и можно считать, что в местообитании проживает достаточное число особей, происходит качественная смена типа динамики – от монотонного роста очень малых величин к ограниченному (логистическому) росту со скоростями порядка репродуктивного потенциала a . Этот рост указывает на то, что рождаемость на этом этапе полностью компенсирует смертность и эмиграцию и происходит активное заселение территории. Вместе с тем ограниченный рост

продолжается до тех пор, пока эмиграционный отток полностью компенсирует рост внутренней конкуренции, однако при достижении некоторых критических плотностей включаются плотностно-зависимые механизмы регуляции, описываемые экспонентой в системе (1), и динамика переходит к устойчивым колебаниям с периодом 2. Соответственно этот этап на рис. 1 а показан серой полосой, где динамика субпопуляций оказывается квазистационарной.

• (III)    На третьем этапе динамика всех субпопуляций становится колебательной и в ряде случаев наблюдается синхронизация. Вместе с тем популяции, близкие к начальной 50-й популяции, часто оказываются не синхронными друг другу, а удаленные могут образовывать кластеры синхронных элементов. Данный факт подтверждается профилями снизу, которые показывают асимптотическую динамику системы (1) через достаточно большое число сезонов ( n >4800).

Вместе с тем время начала второго этапа колонизации существенно определяется радиусом связи и коэффициентом миграции. Причем эта зависимость довольно нетривиальная. Например, увеличение коэффициента миграции m примерно в 6 раз ( m= 0,0157 на рис. 1 а и m= 0,1 на рис. 1 в ) приводит к тому, что полное заполнение ареала произойдет на 80 сезонов позже (230 сезонов на рис. 1 в против 310 на рис. 1 а ), а с ростом радиуса связи P в 20 раз ( P= 1 на рис. 1 в и P= 20 на рис. 1 г ), это произойдет примерно от 6 до 10 раз быстрее, в зависимости от коэффициента миграции (рис. 1 в и рис. 1 г - д ). Кроме того, с ростом радиуса связи второй этап расселения становится короче и практически не наблюдается для больших значений P .

По всей видимости, второй этап, в принципе, возможен лишь в случае сценария удвоения периода, а при сценарии Неймарка-Сакера он не наблюдается и после первого этапа расселения субпопуляции демонстрируют квазипериодиче-ские колебаний либо формируется один из резонансных или мультистабильных режимов. В этом смысле это обобщает ранее полученные результаты в исследованиях расселения в системе связанных популяций с непересекающимися поколениями, описываемых системой локально связанных одномерных отображений Рикера [8].

Серия других вычислительных экспериментов показала, что асимптотический пространственно-временной режим существенно зависит от параметров связи. В частности, при очень слабой связи, как в первых двух случаях на рис. 1, получить хоть какой-нибудь режим синхронизации очень проблематично. В этом случае преимущественно возникает множество небольших кластеров, сосуществующих с кластером несинхронных элементов, т.е. наблюдаются прежде всего фазовые химеры, а полная синхронизация, в том числе кластерная, возможна при довольно большой связи, как в последних двух примерах (рис. 2г-д).

Кроме того, начальная популяция с ненулевой численностью, из которой идет заселение ареала, часто становится неким центром, вокруг которого располагаются несинхронные субпопуляции, и профили на рис. 2 демонстрируют это утверждение. Здесь 50-я субпопуляция, в ряде случаев, оказывается несинхронной соседним, которые, в свою очередь, образуют кластеры довольно причудливых форм.

Помимо прочего, на рис. 2 показано, как усложняются пространственно-временные режимы при разных значениях параметров. Если в первом случае наблюдаются преимущественно синхронные колебания с периодом 4 (за исключением несинхронной начальной популяции и некоторых других), то по мере того как происходит каскад удвоения периода и формируется развитой хаотический режим, все субпопуляции оказываются несинхронными. Причем они окончательно теряют свою синхронность и формируется пространственно-временной хаос лишь после того, как ареал полностью заполнится. Например, в первом и втором случаях (рис. 2 а - б ) сразу после заполнения ареала формируется семь кластеров и один несинхронный элемент, представленный начальной субпопуляцией. Но только в первом случае кластеры оказываются устойчивыми и существуют продолжительное время (на время счета), в то время как во втором они быстро десинхронизируются и уже через 20 итераций имеют абсолютно несинхронное поведение.

Аналогичная ситуация наблюдается и в других примерах, где сразу после колонизации ареала наблюдается один несинхронный элемент и три кластера, расположенные примерно на тех же местах во всех шести случаях (рис. 2 в - з ). Однако в зависимости от параметров связи и начальной численности асимптотические пространственные режимы оказываются принципиально разными. Это, например, несинхронный режим на рис. 2 в , режим сосуществования кластеров с синхронной и несинхронной динамикой на рис. 2 г - е и, наконец, когерентная динамика с разным числом кластеров на рис. 2 ж - з .

Интересно, что разрушение кластеров, которые всегда образуются после полного заполне-

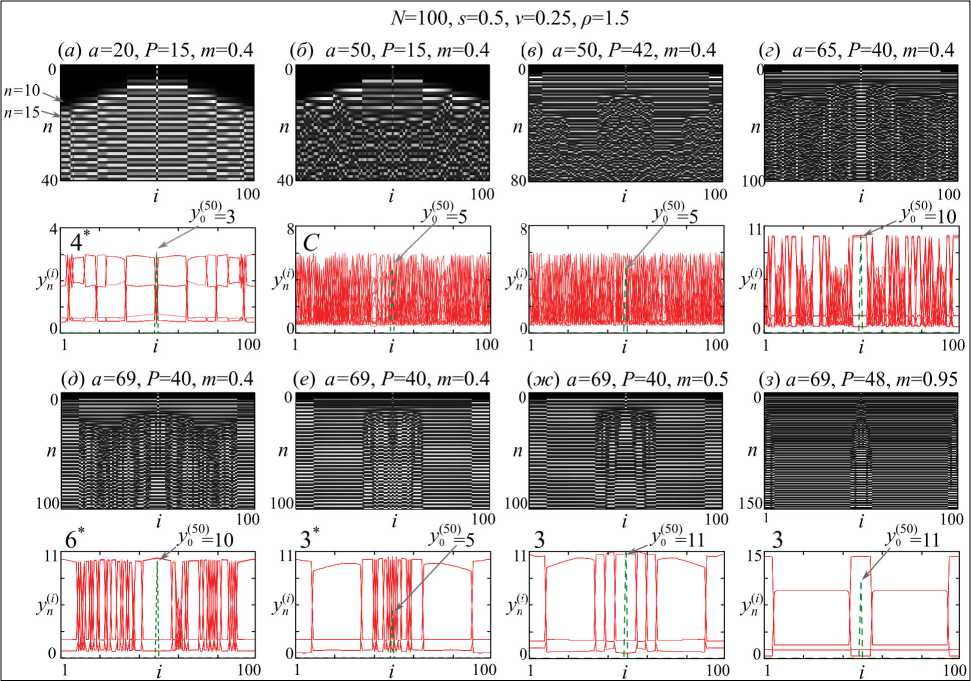
Рис. 2. Ход колонизации (сверху) и профили асимптотических пространственно-временных режимов (снизу) при разных популяционных и миграционных параметрах, а также начальных численностях. Число – регистрируемый период колебаний, C – хаотическая динамика, верхний индекс «*» – химера

Fig. 2. Process of colonization (at the top), and profiles of asymptotic spatial-temporal regimes (below), at different population and migration parameters and the initial population numbers Figure-a detected period of fluctuation, «*» – chimera ния ареала, происходит по-разному. Например, в последних трех примерах (рис. 2е-з) в окрестности начальной популяции, из которой происходит заселение, несинхронными оказываются довольно большое число субпопуляций. Однако в первом (рис. 2е) они остаются несинхронными навсегда, но в последних двух примерах они все же синхронизируются через довольно продолжительный период времени (более 100 и 150 сезонов соответственно) и образуются один (рис. 2ж) или несколько (рис. 2з) кластеров синхронных элементов.

Выводы

Таким образом, в работе обнаружено, что тип пространственно-временной динамики популяций с возрастной структурой существенно определяется управляющими параметрами, а так- же начальными численностями особей в разных частях ареала. Основные типы динамики связаны с когерентным или синхронным поведением связанных популяций, частным проявлением которого является кластерная синхронизация, а также химеры как переходное состояние между синхронным и несинхронным поведением. В этом смысле динамика структурированных популяций демонстрирует мультистабильность в самом широком смысле, которая проявляется в следующем: различные начальные численности приводят не только к кластерам, элементы которых отличаются лишь фазами колебаний («классическая» когерентная динамика), но также разными амплитудами и периодами в смежных кластерах («смешанная» кластерная синхронизация). Например, кластер с хаотической динамикой сосуществует с кластером, испытывающим регулярные колебания, либо кластер синхронных элементов реализуется одновременно с кластером некогерентных элементов. Кроме того, в рамках данной модели описан режим, известный как уединенные состояния [14], интересный тем, что на фоне слабых синхронных или несинхронных колебаний возникают одиночные некогерентные элементы с много большей амплитудой.

С использованием предложенной модели в работе изучен процесс расселения или колонизации изначально пустого ареала из единственной субпопуляции с ненулевой численностью. Показано, что это проходит в три этапа.

На первых двух происходит первичное заполнение ареала, которое сопровождается ограниченным ростом численностей в разных местообитаниях. Выявлено, что колонизация кольцевого ареала с N потенциальными местообитаниями и локальной связью (миграцией на смежные территории) невозможна за короткое время (всегда больше N /2). Кроме того, колонизация идет быстрее при больших коэффициентах миграции и радиусах связи.

На последнем этапе формируются устойчивые колебания, которые в ряде случаев оказываются синхронными, и образуются кластеры. Показано, что существует сложная связь между параметрами связи, начальной численностью и формируемым режимом. В частности, кластеры возможны при сильной связи (радиусе и силе), а при слабой связи возникают преимущественно несинхронные или «смешанные» режимы. Кроме того, оказалось, что после первичного заполнения ареала, до выхода на устойчивый режим, кластеры возникают практически всегда. Однако в зависимости от параметров связи они либо существуют продолжительное время, т.е. оказываются устойчивыми, либо десинхронизируются и формируются некогерентные режимы.