Формирование лазерных пучков Эйри с помощью бинарно-кодированных дифракционных оптических элементов для манипулирования микрочастицами

Благодаря компактной концентрации световой энергии в области малого размера и сохранению такого распределения на значительных расстояниях (т.е. существенное увеличение глубины фокуса по сравнению с гауссовыми лазерными модами) без-дифракционные пучки широко используются в различных приложениях: обработка медицинских изображений, неразрушающее исследование материалов, измерение скорости движущ егося предмета – во всех этих задачах важно свойство инвариантной протяженности бездифракционного пучка, т.к. производятся измерения параметров движущегося или протяженного предмета.

Бездифракционные пучки, дополнительно обладающие орбитальным угловым моментом, привлекают особое внимание. Эффективность их применения уже продемонстрирована в таких областях как оптический захват и многофункциональное манипулирование микро- и нанообъектами (от биологических клеток до атомов), в задачах н елин ейной оптики и физики плазмы . Одним из перспективных направлений является их применение в квантовых вычислениях – бесконечное число ортогональных состояний орбитального углового момента значительно увеличивает количество информации, которая может быть передана одним фотоном.

После того как в конце 80-х годов прошлого века были физически сформированы бесселевые лазерные пучки [1, 2] и была показана эффективность их разнообразного применения, научное сообщество занялось поиском других бездифракционных решений волнового уравнения: параболические пучки [3], гипергеометрические пучки [4, 5], пучки Эйри [6], круговые пучки [7], рассчитывая обогатить без-дифракционные пучки новыми свойствами .

И действительно, например, гипергеометрические пучки , в отличие от бесселевых, имеют более протяженный спектр, что позволяет им на большем расстоянии сохранять бездифракционные свойства при их физической реализации и неизбежном ограничении апертурой [8].

Также было продемонстрировано, что одномерные и двумерные пучки Эйри, в отличие от других бездифракционных пучков, обладают баллистическими свойствами [9], что открывает новые возможности в оптическом манипулировании, напри мер, возможность обойти непрозрачное для лазерного излучения препятствие.

Интерес к ф ункциям Эйри , возникший в конце семидесятых годов прошлого века в контексте квантовой механики [10], был реанимирован в последнее время в связи с новыми возможностями, которые предлагает дифракционная оптика в физической реализации математических абстракций.

Как и бесселевые, функции Эйри являются бесконечно протяженными: экспоненциально спадая при положительных значениях аргумента, при отрицательных значениях демонстрируют осциллирующий характер с плохо затухающей амплитудой [11], поэтому для их физической реализации требуется усечение. В статье [12] были рассмотрены пучки Эйри с конечной энергией, представляющие собой произведение классической моды Эйри и экспоненциальной функции, а в работе [13] получена обобщенная формула, описывающая параксиальное прохождение Эйри-Гауссовых пучков через оптическую ABCD-систему.

Хотя умножение на гауссовую или экспоненци-альн ую функцию (в последнем случае Ф урье-образ пропорционален гауссовой функции) позволяет достаточно просто формировать такие пучки с помощью пространственного модулятора света, освещенного лазерным излучением, в обоих случ аях формируемые пучки фактически п ерестают быть бездифракционными, хотя приблизительно сохраняют свой вид до некоторого расстояния.

В работе [14] был рассмотрен иной способ усечения бесконечной моды Эйри – прямо уголь ной апертурой: от некоторого знач ения d0 в положительной части аргумента (например, значение Ai(x=d0=3) практически равно нулю) и до n-го нуля в отрицательной части. Такое «ограниченное» распред еление Эйри формируется в поперечном сечении мод лазеров «шепч ущей галереи» [15-17]. В статье [14] проводилось сравнение ст епени расходимости трех типов усеченных пуч ков Эйри: экспоненциальных, гауссовых и просто ограниченных диафраг мой и было численно показано , что в последнем случ ае осциллирующая структура пучка и узкий четко выделенный максимум интенсивности сохраняется гораздо дольш е, ч ем в двух первых.

В данной работе также приведены результаты экспериментального формирования одномерных пучков Эйри иным, чем в [6, 12] способом, а именно: с помощью бинарно-кодированных фазовых дифракционных оптических элементов (ДОЭ). При этом с помощью параметров кодирования [18, 19] варьируется энергетический вклад высокочастотных составляющих формируемого пучка и продемонстрирована генерация распределения, бесконечно долго сохраняющего концентрацию энергии в узком боковом лепестке. В дальней зоне к боковому пику добавляется симметричный. Именно такой пучок был использован для захвата полистироловых шариков в спектральной области в двух локализациях и выстраивания их в ряд.

1. Расчет бинарно-кодированных ДОЭ, формирующих ограниченные пучки Эйри

В работе [14] было предложено вместо экспоненциальных пучков Эйри [6] и пучков Эйри-Гаусса [13] формировать ограниченные пучки Эйри:

Эйри-Гауссовый пучок сохраняет свое распределение несколько дольше экспоненциального, но все равно очень быстро вырождается по сравнению с (1). Это связано с сохранением осциллирующего характера структуры функции Эйри, аналогично тому, как моды Бесселя «сопротивляются» дифракции за счет системы периферийных концентрических колец.

Интересно, что если не только отказаться от подавления высокочастотных составляющих при усечении функции Эйри, но даже усилить их, как показано на рис. 1, то такое предискажение исходного распределен ия позволяет сконцентрировать в узком боковом лепестке бесконечно долго (т.е. и в пространственном сп ектре) сохраняющуюся эн ергию. На рис. 2 показано сравнительное распространение в свободном пространстве интенсивности ограниченной функции Эйри (1) и ее аналога с усиленными высокими частотами. Хорошо видно, что в то время как обычная функция Эйри стремится в дальней зоне к прямоугольному распределению, ее искаженный вариант сохраняет четко выраженный боковой пик, к которому добавляется симметричный, как и следовало ожидать в пространственном спектре действительной функции.

Формировать ограниченные пучки Эйри (1) предлагается иным, чем в [6, 12] способом, а именно: с помощью фазовых бинарно-кодированных ДОЭ.

V n ( x , z = 0)

I Ai ( x ) , Y _n <  x < d 0 , [ 0, иначе,

где d о = ⁷ , Y n = ^-

2/3

³^4 n ^- 1 )

– корни ф ункции

Эйри [20], которые в расчетах численно уточнялись.

В [14] было показано, что пучок (1) значительно меньше подвержен дифракции, чем другие типы усеченных пучков.

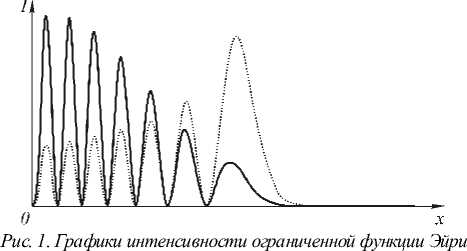
(1) при n=7 (точечная линия), и эта же функция с усиленным вкладом высоких частот (сплошная линия) при z=0

а)

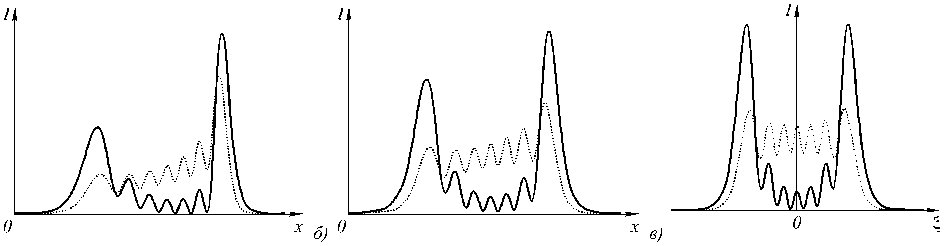
Рис. 2. Графики интенсивности ограниченной функции Эйри (1) при n=7 (точечная линия), и эта же функция с усиленным вкладом высоких частот (сплошная линия) на расстоянии z=0,2z0 (а), z=0,5z0 (б) и Фурье-спектр (в), z0 - расстояние Рэлея

Для выполнения кодирования функции (1) в комплексное распределение с единичной амплитудой и бинарной фазой был применен метод частичного кодирования [18, 19]. Этот метод позволяет варьировать параметры формируемого поля – дифракционную эффективность и погрешность фор- мирования поля – в широких пределах и выбирать для конкретной задачи лучшее их соотношение, т.к. данные параметры являются конкурирующими.

Похожий подход к применению вспомогательных (parity) элементов [21] был рассмотрен в [22]. При кодировании Фурье-образа функции можно ограни- чивать радиус частот, участвующих в кодировании, и тогда при максимальном радиусе выполняется наиболее точное воспроизведение, но и наибольшее «отбрасывание» энергии из полезной области.

Суть метода частичного кодирования [18] в следующем: вводится некоторое пороговое значение a e [0,1] кодируемой амплитуды, выше которого амплитуд а заменяется постоянной величиной, а кодированию (например, двухфазным методом) подвергаются только те точки, где амплитуда светового поля ниже выбранного порога (см. рис. 3). Изменением величины пороговой амплитуды a можно плавно изменять значения погрешности и эффективности при формировании световых полей .

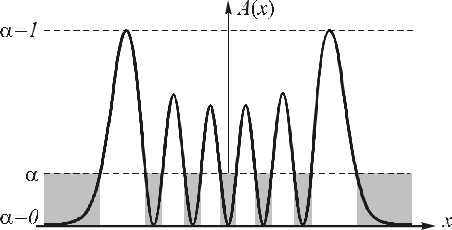
Рис. 3. Иллюстрация к методу частичного кодирования

В таблице 1 показаны кодированные бинарные фазы ДОЭ с различными значениями параметра кодирования a , предназначенные для формирования пучков Эйри (1) при n =7, и их пространственные спектры. При a = 0 кодирование вырождается в метод киноформа, обеспечивающий высокую дифракцио нную эффективность при грубой аппроксимации формируемого распределения. При a = 1 выполняется полное кодирование двухфазовым методом, обеспечивающим высокую точность формирования за счет отбрасывания части энергии из полезной области. Промежуточное значение a = 0,5 соответствует случаю умеренного усиления высоких частот, что подтверждается картиной пространственного спектра.

На рис. 4 приведены распределения интенсивности на различных расстояниях ( z 0 – расстояние Рэлея), формируемые каждым из рассмотренных ДОЭ.

Из табл. 1 и рис. 4 видно, что при a = 1 формируется близкое к идеальному распределение, которое сохраняется на длительном расстоянии, но имеет невысокую дифракционную эффективность . При a = 0 расстояние, на котором пучок Эйри сохраняет выраженный узкий боковой пик, значительно меньше (на расстоянии Рэлея уже происходит полное разрушение структуры), хотя в этом случае в полезную о бласть попадает более 60% падающей энергии. При a = 0,5 распределение также близко к идеальному за исключением высокочастотных составляющих – это хорошо видно как на рис. 4 а , так и в реконфигурации спектральной картины. Данное значение параметра кодирования представляет собой оптимальный компромисс между энергетической эффективностью и точностью формирования.

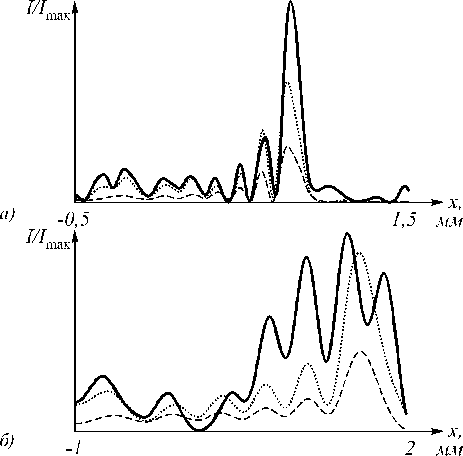
Рис. 4. Графики интенсивности при n=7

для параметров кодирования a = 1 (пунктирная линия), a = 0,5 (точечная линия) и a = 0 (сплошная линия) на расстоянии z=0,4z₀ (a) и z=z₀ (б)

На основании приведенных выше рассуждений для изготовления были выбраны бинарные ДОЭ, рассчитанные при a = 1 и a = 0,5 .

2. Изготовление бинарных ДОЭ

По синтезированным изображениям ДОЭ был изготовлен фотошаблон на стеклянной подложке с напыленным слоем хрома толщиной 100 нм (рис. 5).

Рис.5. Фотошаблон нескольких ДОЭ

Запись фотошаблона производилась на станции лазерной записи CLWS-200 путем создания защитной окисной пленки окиси хрома на засвечиваемых участках с последующим удалением слоя хрома в жидкостном травителе. Точность позиционирования засвечивающего лазерного луча со ставляла 20 нм, а минимальный размер элемента изо бражения составлял 0,6 мкм. Микрофотографии участков фотошаблона представлены на рис. 6.

Рис. 6. Фрагменты фотошаблона для реализации функций Эйри

Изготовление самого ДОЭ про изводило сь стандартными методами жидкостной фотолитографии с использованием фоторезиста ФП-351В на стеклянной подложке толщиной 2,5 мм и показателем преломления 1,51. После процессов нанесения (центрифуга Poloz), сушки и засвечивания (через фотошаблон) фоторезиста подложка подвергалась травлению в растворе плавиковой кислоты с ингибитором из фтористого аммония. Глубина травления составила 0,5 мкм с неравномерностью по площади около 2 %. Погрешность травления по высоте составила около 50 нм. С учетом того , что ДОЭ изготавливался для использования при освещении лазером с длиной волны 532 нм, погрешность отклонения от оптимальной глубины травления 521 нм составляет более 10%. На рис. 7 показан участок изготовленного ДОЭ под микроскопом.

Таблица 1. Кодированные ДОЭ с различными значениями параметра кодирования а , предназначенные для формирования пучков Эйри (1) при n=7, и их пространственные спектры

I

f

I

Рис.7. Участок изготовленного ДОЭ под микроскопом

3.    Экспериментальное формирование модовых пучков Эйри с помощью бинарных ДОЭ

Для проведения экспериментов использовалась оптическая схема, представленная на рис. 8.

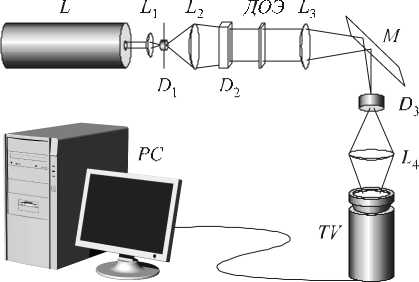
Рис.8. Оптическая схема для формирования пучков Эйри:

L -лазер, L 1 - микрообъектив (20 x ), D 1 - точечная диафрагма, L₂ - коллимирующая линза, D₂ - щелевая диафрагма, DOE - дифракционный оптический элемент, L 3 - линза, выполняющая преобразование Фурье, M -поворотное зеркало, D 3 – диафрагма, отсекающая высокие частоты в фурье –спектре, L₄ – линза, формирующая изображение, TV – CCD камера, PC – персональный компьютер

Световой пучок, выходящий из твердотельного лазера L (длина волны 532 нм), фокусировался микрообъективом (20 x ) на точечной диафрагме D 1 ; пучок, выходящий из диафрагмы, коллимировался линзой L 2 . Размер пучка после коллимации составлял 30 мм. Затем пучок обрезался щелевой диафрагмой D 2 шириной 1 мм. После этого сформированный пучок попадал на ДОЭ (размер 10 x 10мм), фаза которого представлена на рис. 5 (выбирался для освещения соответствующий участок оптического элемента).

Экспериментально зафиксированные распределения интенсивности, формируемые изготовленными бинарными ДОЭ, показаны на рис. 9.

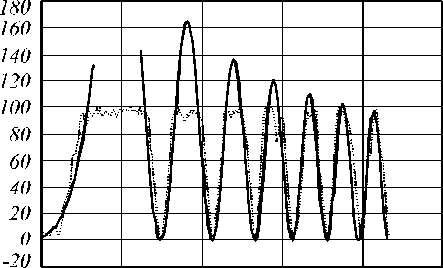
При регистрации интенсивности произошла засветка (перенасыщенность) из-за высокой чувствительности камеры, поэтому о качестве сформированных пучков можно судить только по соответствию нулей экспериментальной функции. На рис. 10 показано наложение аналитической функции на экспериментальные распре-

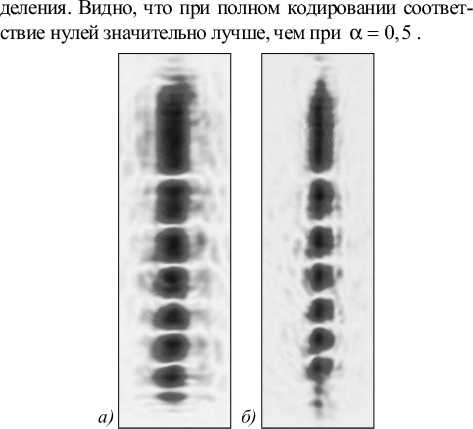
Рис. 9. Экспериментальные распределения интенсивности, сформированные бинарными ДОЭ при уровне частичного кодирования а = 1 (а) и а = 0,5 (б)

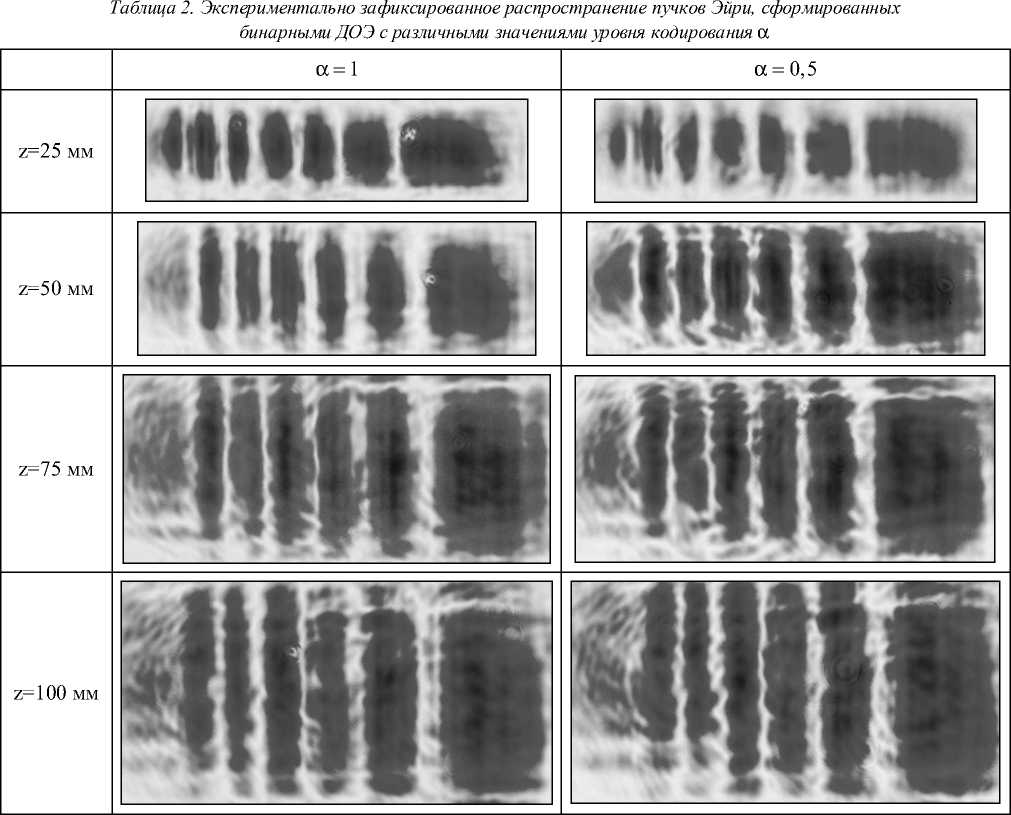
Однако результаты распространения каждого из пучков, показанные в таблице 2, очень похожи с той небольшой разницей, что высокочастотная компонента при а = 0,5 сохраняется немного лучше.

Распро стран ение пучков Эйри фиксировалось в расходящемся пучке линзы L 3 с фокусным расстоянием 400 мм.

Из таблицы 2 видно , что пучки примерно сохраняют одномерную структуру при небольшой расходимости – исходный пучок, имеющий продольный размер 1,5 мм за расстояние в 100 мм, увеличился менее чем на 10%. Поперечное уширение пучка связано с дифракцией на одномерной щели, которая была использована при освещении квадратных ДОЭ.

4.    Оптический захват микрообъектов в пучках Эйри

Для оптического захвата микрообъектов был использован бинарный ДОЭ, формирующий в пространственном спектре два четко выраженных максимума интенсивности (т.е. с усиленными высокочастотными со ставляющими).

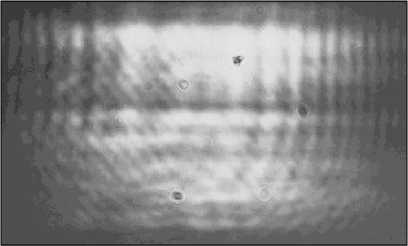
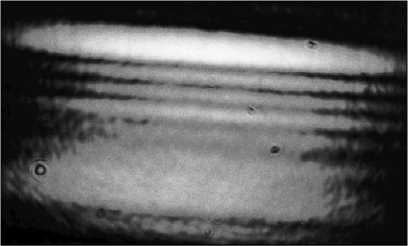
Сравнение распределения интенсивности в фокальной плоскости линзы и вблизи от нее для ДОЭ с различными уровнями кодирования показано в таблице 3. Видно, что полностью кодированный ДОЭ формирует пространственный спектр с распределением, близким к прямоугольному, а частичное кодирование ( а = 0,5) приводит к усилению высоких частот, как и было предсказано при численном моделиро вании (см. раздел 1). При этом даже в случае значительной дефокусировки сохраняется четко выраженный боковой пик интенсивности. Таким образом, пучки Эйри с усиленной высокочастотной со ставляющей позволяют осуществлять уверенный захват микрообъектов в спектральной области. При захвате микрообъекты группируются в двух максимумах.

а)

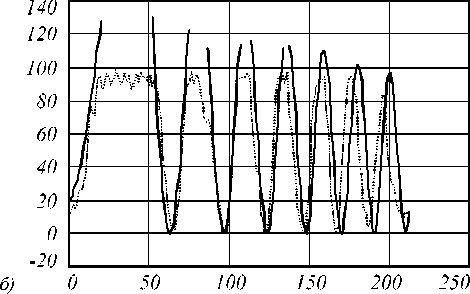
Рис. 10. Соответствие нулей для экспериментального распределения интенсивности при а = 1 (а) и а = 0,5 (б)

Для проведения эксперимента использовалась оптическая схема, представленная на рис. 11.

В данную схему устанавливался ДОЭ, фаза которого представлена рис. 5 для параметра кодирования а =0,5.

Для захвата были использованы полистироловые шарики диаметром 5 мкм. На рис. 12 представлены различные стадии захвата микрообъектов с интервалом 3 с.

Как видно из рис. 12, наблюдается стабильный захват нескольких полистироловых шариков в двух локализациях и выстраивание их в ряд.

Заключение

В работе рассмотрено формирование лазерных пучков Эйри с различными характеристиками дифракционной эффективности и точности с помощью бинарных фазовых дифракционных оптических элементов. Кодирование фазы выполнено методом частичного кодирования при различном значении параметра кодирования а .

Показано, что при а =0,5 происходит формирование пучка Эйри с усилением высокочастотных составляющих.

Таблица 3. Распределения интенсивности, зафиксированное в плоскости фокусировки (фокус линзы равен 400 мм) и на некотором расстоянии от нее, сформированные бинарными ДОЭ с различными значениями уровня кодирования а фокус

а =1                                         а =0,5

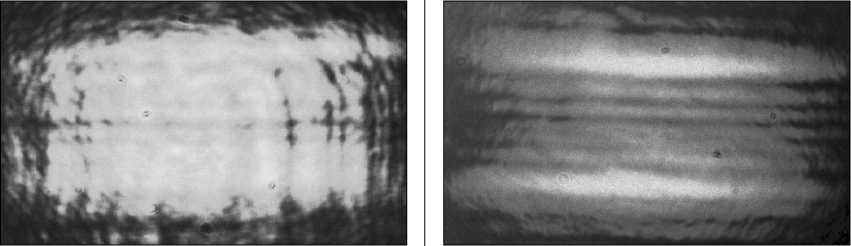
дефокусировка

N z= 50 мм

а)

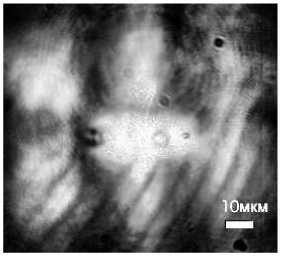
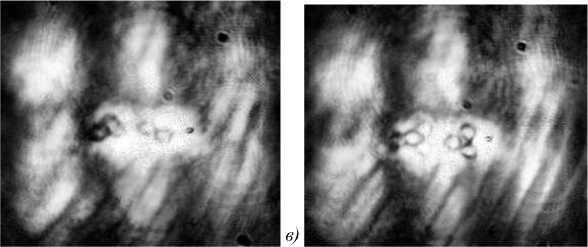
Рис. 12. Захват микрообъектов в пучке Эйри

б)

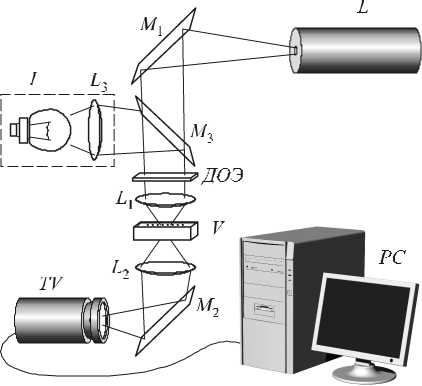
Рис. 11. Оптическая схема для микр ома нипулир ования в пучках Эйри: L -лазер, L 1 - микрообъектив (20 х ), DOE - дифракционный оптический элемент, L₂ - линза, формирующая изображение, M₁, M₂ - п овор отные зеркала, TV – CCD камера, PC – персональный компьютер

На основе синтезированных фазовых распределений при а =1 (полное кодирование) и а =0,5 методом жидкостной фотолитографии изготовлены дифракционные оптические элементы с различным шагом дискретизации.

Экспериментальное исследование сформированных изготовленными ДОЭ пучков показало качественное согласование с численными результатами: примерное сохранение одномерной структуры пучка при небольшой расходимости - исходный пучок, имеющий продольный размер 1,5 мм за расстояние в 100 мм, увеличился менее чем на 10%.

Существенное выделение высокочастотной составляющей для частично-кодированного ДОЭ происходит в спектральной области. Эксперимен-тально показано формирование двух боковых пи -ков интенсивности, в отличие от прямоугольного распределения обычной функции Эйри. При этом даже в случае значительной дефокусировки со -храняется четко выраженный боковой пик интен-сивности.

Таким образом, пучки Эйри с усиленной высокочастотной составляющей позволяют осуществлять уверенный захват микрообъектов в фокальной плоскости линзы, что и было продемонстрировано для полистироловых шариков.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки вед ущих научных школ (НШ-3086.2008.9) и гранта РФФИ 08-07-99007.