Формирование микрорельефа дифракционных оптических элементов с использованием достижений микроэлектроники

Дифракционный оптический элемент (ДОЭ) представляет собой зонную пластинку с дифракционным микрорельефом, отображающим фазовую функцию [1]. С точки зрения практической реализации ДОЭ наибольшее распространение получили два типа фазового микрорельефа (рис. 1): ступенчатый (бинарный и многоуровневый) и кусочнонепрерывный.

Рис. 1. Профили микрорельефов ДОЭ:

• (а)    — бинарный; (б) — многоуровневый;

• (в) — кусочно-непрерывный

Особое внимание специалистов в области дифракционной оптики привлекают технологии формирования микрорельефа, основанные на достижениях и оборудовании микроэлектроники [1], в частности, использование фотолитографических методов.

Перенос рисунка микрорельефа ДОЭ в поверхностный слой подложки с использованием метода фотолитографии [2, 3] происходит в четыре стадии (рис. 2): 1) экспонирование слоя фоторезиста через шаблон и образование скрытого изображения; 2) проявление и задубливание рисунка, т.е. формирование защитной маски; 3) травление поверхностного слоя подложки на незащищенных участках; 4) очистка поверхности подложки от остатков фоторезиста [4].

На каждой из стадий процесса действуют факторы, искажающие исходный рисунок шаблона. При экспонировании имеют место явления дифракции, преломления и отражения света, приводящие к изменению размеров элементов рисунка и размытости их краев. Искажения размеров на втором этапе (проявления и задубливания) обусловлены набуханием слоя фоторезиста и усадкой фотомаски при тепловой обработке. При травлении негативным фактором является боковое подтравливание под маску. Условия, в которых происходит обработка на разных стадиях, изменяются как от пластины к пластине, так и в пределах одной пластины. Это приводит к разбросу геометрических параметров микрорельефа и, соответственно, характеристик оптического элемента, что следует учитывать при отработке технологии изготовления ДОЭ.

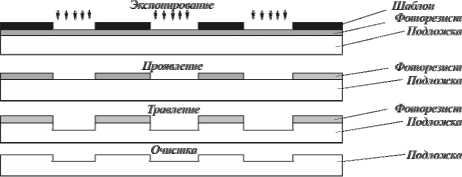
Рис. 2. Процесс формирования микрорельефа в подложке

С конструктивной точки зрения ДОЭ следует рассматривать в качестве сложного изделия, состоящего из чрезвычайно большого количества конструкционных микроэлементов субмикронных размеров. Как правило, для получения высокой дифракционной эффективности ДОЭ с многоуровневым микрорельефом рассчитанный профиль зон микрорельефа аппроксимируют не менее чем восьмью градациями, что приводит к необходимости совмещения как минимум трех шаблонов. Требования к точности изготовления каждой части изображения аппроксимированной зоны при этом возрастают на порядок по сравнению с требованиями к точности целиком изображенной зоны, что резко повышает требования к технологическому оборудованию.

Оценка преемственности использования микротехнологий при создании ДОЭ

Для оценки возможности использования технологического оборудования микроэлектроники проанализируем взаимосвязь конструктивных размеров микрорельефа с параметрами, которым должен удовлетворять ДОЭ как оптический элемент.

Трудности практической реализации ДОЭ обусловлены необходимостью создания поверхностного микрорельефа [1], максимальная высота которо- го, исходя из длины волны λ и коэффициента преломления среды n, определяется:

hmax = λ/(n - 1).(1)

Менее важной, но существенной, является величина ширины зоны:

∆J = rJ -rJ-1, j = 1,2,…k ,(2)

где j – порядковый номер зоны; r j - радиусы Френеля дифракционной линзы, определяемые приблизительно как:

rj =(2λf j)1/2,(3)

где f – фокусное расстояние элемента.

Из выражений (2) и (3) следует, что ширина зон является переменной и уменьшается к периферии линзы. Присутствие в выражениях (1) и (3) параметра λ свидетельствует о том, что основополагающие параметры микрорельефа h max и ∆ j min могут достигать весьма малых значений (см. таб. 1 при n=1,5).

Таблица 1.

Зависимость параметров микрорельефа от длины волны для различных фокусных расстояний оптического элемента

Фокусное расстояние, мм	λ , мкм	∆ 1, мм	∆ 50, мм	h max, мкм
500	1,0	1,0	0,07	2,0
	0,5	0,71	0,05	1,0
	0,1	0,32	0,02	0,2
100	1,0	0,46	0,03	2,0
	0,5	0,32	0,02	1,0
	0,1	0,14	0,01	0,2

Значимость размерных факторов микрорельефа ДОЭ еще более возрастает, если принять во внимание необходимость обеспечения точностных параметров последних. Предельно допустимые отклонения характеристических параметров микрорельефа ДОЭ в зависимости от принимаемого допуска η при его изготовлении с учетом фокусного расстояния приведены в таблице 2.

При реализации фазовой функции ступенчатой аппроксимацией сложный профиль поверхности ДОЭ заменяется совокупностью микроуступов рав- ной толщины hmax/m, где m – число уровней квантования фазовой функции. В рамках настоящей работы квантование предполагает построение ступенчатого профиля фазовой функции ДОЭ с помощью набора элементарных кубиков. Для оценки объема подобного кубика примем размер его ребра равным:

L = h _max / m .                                    (5)

В этом случае количество элементарных кубов, образующих ДОЭ, составит:

N = π D ² m ³ /8 h m ² ax .                         (6)

В частности, для ДОЭ оптического диапазона ( λ =0,5 мкм; D =10мм; m =4; n =1,5) значение параметра N =2,5∙10⁹.

Согласно основополагающим представлениям статистической физики все термодинамические параметры макроскопических объектов испытывают флуктуации от своих средних значений. Актуальность учета флуктуационных процессов в рассматриваемом случае обусловлена:

• а)    малым количеством атомов рабочей среды, содержащихся в пределах элементарного куба, - порядка 10⁸;

• б)    большим количеством элементарных кубов (около 10⁹).

Учитывая широкое разнообразие термодинамических параметров рабочих сред и элементарных физико-химических процессов, составляющих основу технологии создания ДОЭ, можно принять, что флуктуационные процессы являются гауссовыми. В этом случае, абстрагируясь от эффектов корреляции индивидуальных термодинамических параметров, для частот отказов в реализации элементарных кубов по линейному размеру имеем [5]:

2 ^∞

S = 1 -      ∫ exp( - γ ² / 2) d γ ^,             (7)

2π γ

где γ = ηλ / ma ; η - допуск на линейный размер элементарного куба; a – математическое ожидание размытия края топологического элемента. В выражении (7) параметр a выступает в качестве фактора, определяющего разрешающую способность технологического процесса (в случае использования микротехнологий a = 0,01 ÷ 0,1 мкм [2]).

Таблица 2.

Зависимость допустимых отклонений параметров микрорельефа от длины волны для различных фокусных расстояний оптического элемента

Фокусное расстояние, мм	λ , мкм	∆ 1 (мкм)		∆ 50 (мкм)		h max (Å)
		η	η	η	η	η	η
		0,01	0,1	0,01	0,1	0,01	0,1
500	1,0	10,0	100	0,7	7	200	2 x 103
	0,5	7,1	71	0,5	5	100	103
	0,1	3,2	32	0,2	2	20	200
100	1,0	4,5	45	0,3	3	200	2 x 103
	0,5	3,2	32	0,2	2	100	103
	0,1	1,4	14	0,1	1	20	200

Таблица 3.

Частота отказов S в зависимости от предполагаемого допуска п и безразмерного параметра Л / та

п	X / т a
	5	10	50	100	500
0,01	0,9602	0,9204	0,6170	0,3174	6x10-8
0,02	0,9204	0,8414	0,3174	0,0456	<    10-8
0,05	0,8026	0,6170	0,0124	6x10-8	<    10-8
0,10	0,6176	0,3174	6x10-8	<    10-8	<    10-8
0,20	0,3174	0,4560	<   10-8	10-8	<    10-8

В таб. 3 представлены численные значения частоты отказа в зависимости от предполагаемого допуска п и безразмерного параметра Л / та

Данные таб. 3 свидетельствуют о том, что получение микрорельефа ДОЭ с высоким разрешением и малой частотой отказов ( п® 0,01; количество дефектных элементарных кубиков менее 10) весьма проблематично. В то же время снижение требования к качеству микрорельефа в целом (до уровня 70– 90 % бездефектных кубиков от общего числа) может обеспечить приемлемость использования современных микротехнологий. В последнем случае (при X =0,5 мкм; т =4; N =10 9 ) значения технологического фактора a должны удовлетворять условию:

a =

2,5 х 10 - 3 мкм , при п = 0,01;

5,0 х 10 - 3 мкм , при п = 0,05;

2,5 х 10² мкм , при п = 0,10.

Приведенные данные подтверждают, что технологические трудности создания микрорельефа существенно уменьшаются при увеличении рабочей длины волны ДОЭ. Это обусловлено как уменьшением значения параметра ( N =10⁶), так и увеличением характеристического параметра X / ma . В частности, для ДОЭ ИК–диапазона обеспечивается необходимое качество микрорельефа (при Л =10 мкм) на уровне 99,9 % .

Влияние технологических ошибок на качество работы ДОЭ

Параметры ДОЭ определяются конструктивными параметрами микрорельефа, трудности формирования которого обусловлены не только предельными возможностями технологического оборудования, но и технологическими ошибками, возникающими непосредственно при изготовлении ДОЭ . Наиболее значимыми являются ошибки, возникающие при травлении подложки на определенную глубину и при совмещении очередного шаблона с ранее сформированной структурой. Впервые оценка допустимого рассовмещения рассмотрена в работах [6, 7], где предложена методика оценки, состоящая в вычислении фактора Штреля на основе расчета функции зрачка реальной дифракционной линзы (ДЛ). Влияние ошибок, возникающих при травлении микрорельефа на определенную глубину, рассматривалось в работах [8, 9]. В данных работах путем аналитического решения оценена взаимосвязь дифракционной эффективности ДЛ с относительным отклонением глубины микрорельефа в пре- делах ±30%. В работе [10] предложен метод оценки влияния технологических ошибок при формировании микрорельефа ДЛ на световое поле в дальней зоне дифракции, продолжением которой является данная работа. В настоящей статье на примере аксикона моделируется взаимосвязь интенсивности в рабочей зоне элемента и числа уровней квантования, а также анализируется влияние перетрава на среднеквадратичное отклонение распределения интенсивности от идеального на примере четырехуровневой структуры ДОЭ .

Влияние квантования

Влияние квантования фазовой функции на качество работы фокусирующих ДОЭ подробно разобрано в главе 5 монографии [1]. В качестве характеристик, используемых для оценки качества работы фокусирующих ДОЭ, в [1] используется дифракционная эффективность фокусировки и среднеквадратичное отклонение полученного распределения интенсивности от требуемого. Для других типов дифракционных оптических элементов в работе [10] предложено использовать среднеквадратичное отклонение распределений интенсивности, полученных для идеального и исследуемого оптических элементов. Для таких оценок использовалось рассчитанное световое поле в рабочей области ДОЭ. Результаты моделирования, демонстрирующие влияние числа уровней квантования на параметры дифракционных элементов на примере аксикона, представлены на рис. 3-5. Все рисунки относятся к аксикону нулевого порядка диаметром 0,5 мм и с периодом линий 0,05 мм, работающего как дополнение к линзе.

Анализ рис. 3 (б, в) показывает, что кроме главного центрального кольца в дифракционной картине также присутствует набор дополнительных колец, сопоставимых по энергии с главным. Если сравнивать данную картину дифракции с картиной дифракции от идеального аксикона с бесконечным числом уровней квантования, то мы получим среднеквадратичное отклонение (с.к.о.) σ распределений интенсивности около 0,65. Здесь [10]

- = 1!

m 2 i , j          i , j

( I i , j )²

где Ii,j - распределение интенсивности в фокальной плоскости идеального аксикона, Im - распределение i,j интенсивности в фокальной плоскости квантованного аксикона с числом уровней квантования m.

а)

в)

GR

б)

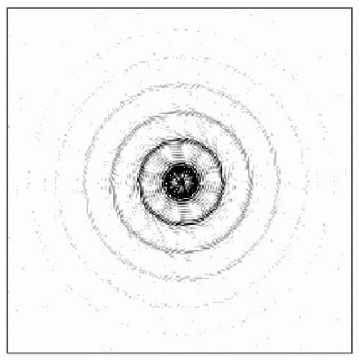
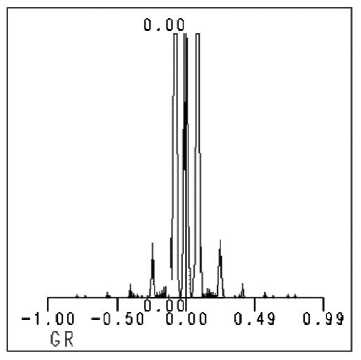
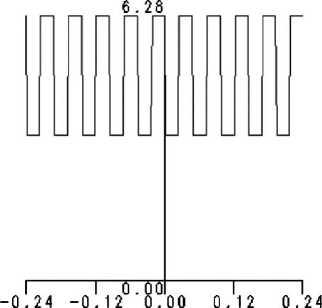
Рис. 3. Параметры бинарной структуры:

(а) - профиль микрорельефа, (б) - дифракционная картина в фокальной плоскости,

(в) - распределение интенсивности в радиальном сечении фокальной плоскости

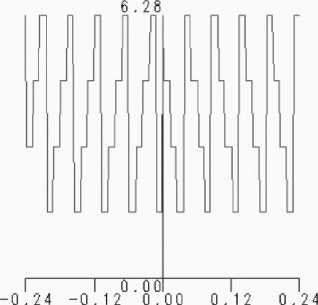
На рис.4 (б, в) также кроме главного центрального кольца в дифракционной картине присутствует набор дополнительных колец. Если сравнивать данную картину дифракции с картиной дифракции от идеального аксикона с бесконечным числом уровней квантования, то мы получим с.к.о. σ около 0,25.

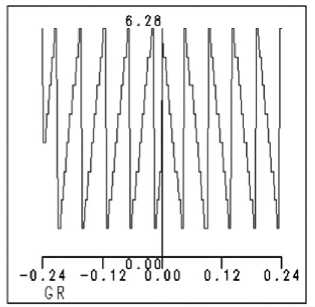
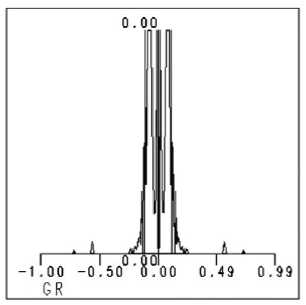
Картина дифракции, представленная на рис . 5 (б), более близка к картине дифракции от идеального акси-кона, значение с.к.о. σ составляет всего 0,07.

а)

в)

GR

б)

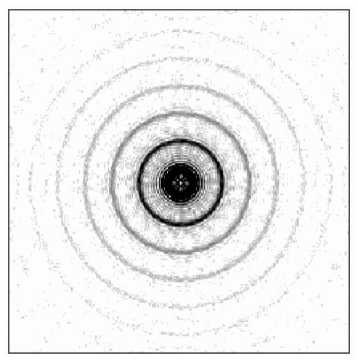
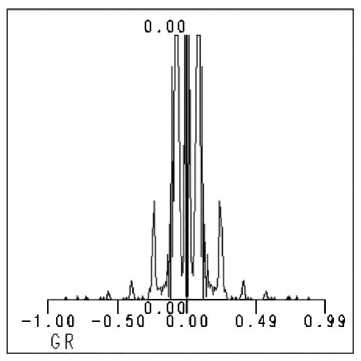
Рис. 4. Параметры четырехуровневой структуры: (а) - профиль микрорельефа, (б) - дифракционная картина в фокальной плоскости, (в) - распределение интенсивности в радиальном сечении фокальной плоскости

Представленные на рис. 3-5 результаты моделирования, позволяют наглядно продемонстрировать влияние числа уровней квантования на параметры элемента. Однако особенно интересным представляется изменение дифракционной картины в фокальной плоскости при отклонении параметров многоуровневого микрорельефа от расчетных значений, в частности, зависимость качества работы ДОЭ от ошибок в глубине степенного травления на каждом этапе.

а)

б)

• в)

Рис. 5. Параметры восьмиуровневой структуры: (а) - профиль микрорельефа, (б) – дифракционная картина в фокальной плоскости,

(в) – распределение интенсивности в радиальном сечении фокальной плоскости

Влияние ошибок глубины травления

Влияние технологической ошибки, связанной с глубиной травления, на параметры интенсивности в фокальной плоскости аксикона можно проследить на рис. 6.

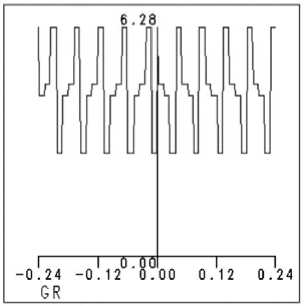
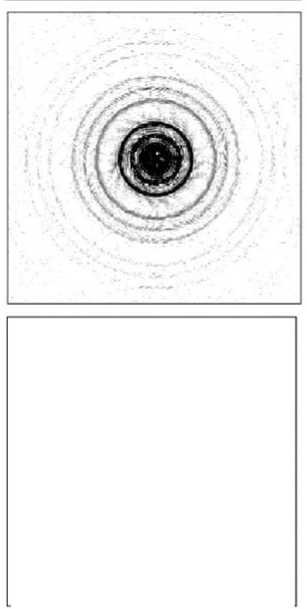
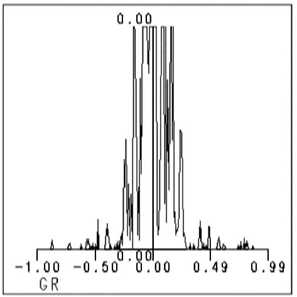
При моделировании ошибок глубины травления микрорельефа предполагается, что на l -той стадии изготовления допущена ошибка размером 5 _l • h i , где hi=h max /2^l - глубина травления на l -том этапе степенного формирования многоуровневого микрорельефа, h max - максимальная высота непрерывного микрорельефа ДОЭ, l - этап травления (достигаемое на нем число уровней квантования фазовой функции m =2 ¹ ). На рис. 6 (а) представлен профиль рельефа ДОЭ, в котором на второй стадии изготовления (для рис. 6 - l =2) была допущена ошибка размером 0,6^/[4( n -1)], где 5₂=0,6; h max =А/( n -1); l =2; m =4. Вследствие этого

5 2 =0,6; h max =Х/( n -1); l =2; m =4. Вследствие этого картина дифракции, представленная на Рис.66, заметно отличается от картины дифракции идеального аксикона, значение с.к.о. о составляет 0,43.

а)

б)

в)

Рис. 6. Четырехуровневая структура, моделирование влияния ошибок травления при выполнении второй технологической операции: (а) - профиль микрорельефа - перетрав,

• (б)    – дифракционная картина в фокальной плоскости, (в) – распределение интенсивности в радиальном сечении фокальной плоскости)

Дальнейшее исследование проведем на примере изменения распределения интенсивности в дальней зоне дифракционной линзы. В качестве критерия оценки, характеризующего качество работы ДОЭ, используется среднеквадратичная ошибка формирования интенсивности в зоне дифракции Фраунгофера, рассчитываемая по формуле (9), где I i j - интенсивность, регистрируемая для линзы с гладкой фазой, I m. - интенсивность, регистрируемая для линзы с квантованной или искаженной фазой.

Пользуясь той же методологией можно привести результаты оценки влияния ошибок травления на среднеквадратичную ошибку формирования интенсивности в зоне дифракции Фраунгофера при несоблюдении технологических режимов (рис. 7).

Для 4-х уровневой линзы σ зависит от ошибки δ 1 более существенно, чем от ошибки δ 2, а при изготовлении 8-ми уровневой структур ы δ 3 вносит наименьшую погрешность. В таб. 4 и 5 для сравнения приведены некоторые сочетания ошибок и их влияние на среднеквадратичную ошибку формирования интенсивности в зоне дифракции Фраунгофера.

Интенсивность, используемая в расчетах, определялась не по всему растру изображения, который был получен после преобразования Фурье, а в квадратной области, размер которой определялся исходя из положения первого минимума интенсивности в фокальной плоскости неискаженной линзы.

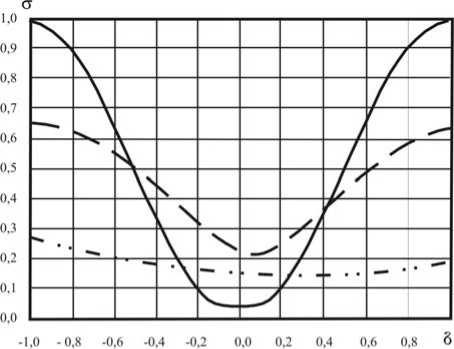
Рис. 7. Графики зависимости ошибки формирования светового поля в дальней зоне дифракции от технологических ошибок, возникающих при травлении: непрерывная линия (—) - первый шаблон ( δ 1 ), пунктирная линия (- - ) - второй шаблон ( δ 2 ), штрих-пунктирная (--ּּ –) - третий шаблон ( δ 3 )

Таблица 4

Зависимость среднеквадратичной ошибки формирования интенсивности в зоне дифракции Фраунгофера σ для сферической линзы при некоторых сочетаниях ошибок δ1 и δ2

δ 1 \ δ 2	-1	-0,9	-0,8	-0,7	-0,6	-0,5	-0,4	-0,3	-0,2	-0,1	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
0,00	0,651	0,644	0,623	0,589	0,543	0,487	0,424	0,357	0,294	0,245	0,226	0,245	0,294	0,357	0,424	0,487	0,543	0,589	0,623	0,643
0,10	0,641	0,632	0,611	0,579	0,536	0,483	0,424	0,363	0,305	0,262	0,247	0,268	0,316	0,380	0,449	0,516	0,578	0,631	0,674	0,705
0,20	0,617	0,608	0,591	0,563	0,525	0,479	0,433	0,398	0,389	0,420	0,489	0,588	0,706	0,833	0,962	1,088	1,206	1,314	1,408	1,485
-0,10	0,641	0,637	0,623	0,599	0,568	0,533	0,497	0,465	0,444	0,437	0,448	0,473	0,511	0,555	0,600	0,643	0,679	0,707	0,725	0,731
-0,20	0,617	0,620	0,622	0,631	0,652	0,691	0,748	0,824	0,914	1,012	1,115	1,217	1,314	1,401	1,476	1,535	1,577	1,599	1,601	1,583

Таблица 5

Значения среднеквадратичной ошибки формирования интенсивности в зоне дифракции Фраунгофера σ для сферической линзы при некоторых сочетаниях ошибок δ1, δ2, δ3

δ3 \ δ 1 δ2,	0 0	0,1 0	-0,1 0	0 0,1	0 -0,1	0,1 0,1	0,1 -0,1	-0,1 0,1	-0,1 -0,1
-1,0	0,286	0,312	0,519	0,284	0,315	0,306	0,343	0,478	0,573
-0,9	0,265	0,295	0,506	0,262	0,297	0,288	0,329	0,463	0,563
-0,8	0,246	0,281	0,493	0,241	0,282	0,272	0,317	0,448	0,552
-0,7	0,228	0,269	0,481	0,222	0,268	0,259	0,307	0,434	0,542
-0,6	0,213	0,259	0,469	0,205	0,256	0,247	0,299	0,421	0,531
-0,5	0,199	0,251	0,457	0,190	0,245	0,238	0,292	0,408	0,520
-0,4	0,188	0,244	0,445	0,176	0,235	0,230	0,287	0,395	0,509
-0,3	0,178	0,240	0,433	0,164	0,227	0,224	0,282	0,382	0,497
-0,2	0,170	0,236	0,421	0,154	0,220	0,220	0,278	0,369	0,485
-0,1	0,163	0,234	0,408	0,146	0,214	0,217	0,275	0,357	0,472
0,0	0,158	0,232	0,396	0,139	0,208	0,215	0,273	0,345	0,459
0,1	0,154	0,231	0,383	0,134	0,204	0,214	0,270	0,333	0,445
0,2	0,152	0,231	0,371	0,132	0,200	0,213	0,269	0,322	0,431
0,3	0,152	0,232	0,360	0,132	0,198	0,214	0,267	0,312	0,418
0,4	0,154	0,233	0,349	0,135	0,197	0,216	0,267	0,303	0,405
0,5	0,159	0,236	0,339	0,140	0,198	0,220	0,268	0,296	0,392
0,6	0,166	0,240	0,331	0,149	0,202	0,225	0,269	0,291	0,381
0,7	0,176	0,246	0,325	0,161	0,208	0,231	0,273	0,288	0,372
0,8	0,189	0,254	0,322	0,176	0,217	0,240	0,278	0,289	0,365
0,9	0,205	0,264	0,322	0,194	0,229	0,251	0,286	0,293	0,361

Ввиду этого в вычислительном эксперименте могут быть получены значения σ больше 1 (при большом отклонении глубины полученного микрорельефа от расчетного).

Следует обратить внимание, что в таб. 5 имеются одинаковые значения среднеквадратичной ошибки формирования интенсивности соответствующие различным значениям технологических погрешностей: например, о=0,286 при ( 5 1 = 5 2 = 0; 5 3 =-1) и при ( 5 1 = 0,1; 5 2 = -0,1; 5 3 =0,9) и др., что позволяет предусматривать и осуществлять корректировку некоторых параметров ДОЭ.

Моделирование смещения шаблонов

При формировании многоуровневого микрорельефа ДОЭ имеет место появление таких ошибок, как смещение и поворот относительно продольной оси для цилиндрической линзы и осевое смещение для сферической линзы, возникающих при наложении очередного шаблона на ранее изготовленный микрорельеф.

В ходе вычислительного эксперимента осуществлялись одно- и разнонаправленный сдвиги 2-ой и 3-ей виртуальных масок относительно друг друга и первой маски, а затем анализировалось световое поле в зоне дифракции Фраунгофера. Сдвиг осуществлялся не относительно реальных размеров масок, а по отсчетам дискретизации - для удобства проведения вычислительного эксперимента. В качестве примера на рис.8 приведены результаты вычислительного эксперимента для дифракционной сферической линзы, у которой вторая маска сдвигалась относительно «протравленного микрорельефа» до 5-ти отсчетов, а третья маска относительно второй -до 20-и отсчетов. Диаметр линзы – 1 мм, фокусное расстояние – 1000 мм, размер отсчета технологической маски – 2 мкм.

σ

2 1,75 1,5 1,25 1 0,75 0,5 0,25 0

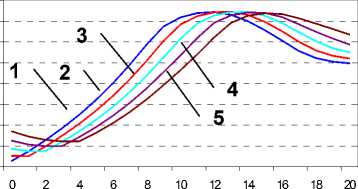
______________________ Сдвиг третьей маски

Рис. 8. Зависимость с.к.о. формирования интенсивности дифракционной сферической линзой в дальней зоне дифракции от сдвига третьей маски, при этом вторая маска сдвигается на 0 (1), 1 (2), 2 (3), 3 (4), 4 (5) отсчетов соответственно

Анализ результатов моделирования (рис. 8) также позволяет отметить возможность некоторой корректировки технологических ошибок соответствующим смещением масок.

Заключение

Проанализированы технологические трудности формирования микрорельефа ДОЭ и оценены предельно допустимые отклонения характеристик микрорельефа в зависимости от технологических допусков. На примере аксикона и дифракционной линзы с помощью моделирования и численного эксперимента исследовано влияние технологических ошибок формирования микрорельефа на параметры ДОЭ. Результаты моделирования были апробированы при создании бинарного дифракционного элемента, описанного в [11], и могут быть использованы для предварительной оценки параметров изготавливаемых ДОЭ.