Формирование мод Гаусса-Эрмита с помощью бинарных ДОЭ. I. Моделирование и эксперимент

В [1,2] показано теоретически, что для эффективного формирования одномерных мод Гаусса-Эрмита (ГЭ) можно использовать фазовые бинарные ДОЭ, которые получаются с помощью знаковой функции от соответствующего многочлена Эрмита. При освещении такого ДОЭ плоским пучком света с оптимально подобранной апертурой в дальней зоне дифракции формируется с эффективностью более 80% требуемая мода.

В [3 ] для формирования лазерной моды ГЭ (1,0) был изготовлен и исследован экспериментально фазовый 16-ти уровневый ДОЭ. Он был изготовлен по технологии электронной литографии с помощью травления поли-метилметакрелата, нанесенного на подложку из кварцевого стекла. Этот элемент был рассчитан с помощью итеративной процедуры, предложенной в [4]. Размерность массива была равна 2048x2048 отсчетов. Теоретическая эффективность равнялась 45.5%, а экспериментально измеренная - 37.7%.

В данной работе приведены результаты по безитерационному расчету и исследованию двухуровневых (бинарных) ДОЭ, формирующих моды ГЭ с номерами (1,0), (1,1) и (1,2) с теоретической эффективностью около 70%. Кроме того, результаты работ [1,2] обобщаются на двумерный случай формирования мод ГЭ.

С помощью технологии электронной литографии получены несколько фазовых бинарных ДОЭ. согласованных с модами ГЭ и проведена экспериментальная апробация их работоспособности.

2.    Расчетные формулы

Для эффективного формирования отдельных мод ГЭ предлагается использовать фаговый элемент с функцией пропускания:

^(^J')= sgn^m(x)x х sgn Нп (у) reel — rect —

где /^wCr),£fMCy) - многочлены Эрмита т-го и п-го f 1, х > 0 f х) fl,W^o порядков, sgn(x) = (         , rect - = ],

[-1,х<0 \а) [0,|х|>«

В [1] на основе разложения в ряд одномерной знаковой функции из уравнения (1)

sgnMAx) = i,C^H„W,(2)

р=0

где

^'^Т^^^m

2         -ад(3)

xexp(-x2)#p(x)dx

Из уравнения (5) получается, что с эффективностью около 86% бинарный ДОЭ с пропусканием sgn //, (х) сформирует моду ГЭ, пропорциональную многочлену Н_х (х).

Дтя двумерных ДОЭ с пропусканием (1) эффективность, очевидно, можно оценить как произведение одномерных эффективностей: 0.86x0.86x100% = 73.96%. Эта оценка подтверждается на основании результатов моделирования.

В Таблице 1 приведены значения среднеквадратичного отклонения 6 и эффективности ц, рассчитанных по следующим формулам:

J/{|з[г(х,у)]|2 -^Л^^ГР dxd.y

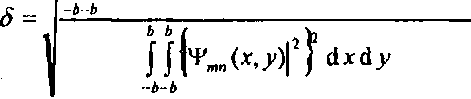
b b                                       2

f J 3[r(x, yofc (x, у') d xd у

-b b

77 ~ T"a ----------------П--

Jfl^x^))!2 dxdyj Л^Дх,^2 dxdy

-b-b                        -b-b

получены выражения в виде конечных сумм для коэффициентов С^, например, при p=2s:

где

( у2 + у2 I

TUx^exp -—к(х)ад ■   (9)

х (-1/ ехр(-х^ )Я₂,_Ч (х_и)

А=1

где xti - нули многочлена: ^2/4.](Ху) = 0 .

С помощью уравнения (4) можно получить конкретные значения коэффициентов для разложения в ряд (2) для каждой моды ГЭ.

Например, для моды ГЭ (1,1)

sgn Н_х i (х, у) = sgn(x) ■ sgn(y)

используя представление:

^’Х^Т^ТТ^"1"-1^    <5)

у Я л-0 2 (2Л4-1)Л!

можно записать:

sgn//n(x,.y)=—х xf^to-T-^to+^ffslx)-...^     <6)

x^to-^W+^/W'.J

Таблица 1.

Рассчитанные средние ошибки и эффективность при формировании мод ГЭ с помощью бинарных знаковых ДОЭ с квадратной апертурой оптимального размера

ТЕММ«>	(1,0)	(1Л)	(1,2)	(7,0)
5, %	28,8	14.4	30.6	62.4
И» %	63.8	72.3	68.5	33.5

Область интегрирования [-6,Ь]х[-й,Л] в уравнениях (7) и (8) выбиралась из условия, что |кРтл(х,у')|' ^ 10 ^. В уравнениях (7) и (8) использовано обозначение преобразования Фурье от функции пропускания ДОЭ:

З[т(х,у)]= J jr(x,y)x хехр

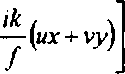
(Ю)

Однако, на практике часто используют не квадратную, а круглую диафрагму, в этом случае мы получим результат немного лучше или хуже, но примерно такой же (см.Таблицу 2)

Таблица 2. Рассчитанные средние ошибки и эффективность при формировании мод ГЭ с помощью бинарных знаковых ДОЭ с круглой апертурой оптимального размера

ТЕММл)	(1,0)	(1,1)	(1,2)	(7,0)
5, %	26.9	15.6	31.8	66.9
	70.1	69.5	65.4	40.7

3.    Изготовление ДОЭ

Бинарные фазовые ДОЭ, функция пропускания которых удовлетворяет уравнению (1), были изготовлены с помощью низковольтового электронного генератора изображений Leica LION LV1 в Университете Йоснсуу (Финляндия). Предельное разрешение этого электронного литографа около 0.04 микрона.

Амплитудная бинарная маска была рассчитана с размерами 1 мм х 1 мм (1000 х 1000 отсчетов) с дискретностью 1 микрон. Высота бинарного рельефа формировалась для длины волны X = 0.633 микрона.

Этапы изготовления бинарного профиля показаны на рис. 1. С помощью электронного луча в слое полиметилметакрелата (ПММА). толщиной 0.18 микрон, который был осажден на подложке из расплавленного оксида кремния SiO2, рисовалось изображение в соответствии с рассчитанной маской (этап 1 на рис.1). После проявления слой хрома толщиной 0.05 микрон осаждался в вакууме на поверхность структуры с бинарным изображением. Затем использовались процедуры вымывания для удаления оставшегося резиста ПММА вместе со слоем хрома из областей нс подвергшихся экспонированию (этап 2 на рис. Г). И наконец, с помощью реактивного ионного травления, при котором слой хрома выступал в качестве защитной маски, в расплавленном оксиде кремния создавался требуемый бинарный профиль (этап 3 на рис. 1). Так как показатель преломления SiO2 равен 1.46, то высота ступеньки бинарного профиля формировалась равной 0.675 микрон.          _____________

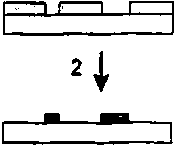
Рис.1. Этаны изготовления бинарного рельефа ДОЭ: I) экспонирование резиста электронным пучком;

• 2)    осаждение хрома и вымывание резиста;

• 3)    реактивное ионное травление

4.    Эксперимент

На рис. 2 показан увеличенный под микроско пом участок получившегося фазового бинарного

ДОЭ.

Рис. 2 Вид участка фазового бинарного ДОЭ под микроскопом

Изготовленные по литографической технологии бинарные фазовые ДОЭ исследовались на установке, оптическая схема которой показана на рис. 3. Луч света от He-Ne лазера малой мощности расширялся микрообъективом и фильтровался с помощью малой круглой диафрагмы. После коллимирования расходящегося пучка он ограничивался другой круглой диафрагмой радиусом примерно 1.1-1.2 мм. Ограниченный по радиусу плоский пучок попадал затем на бинарный ДОЭ. Дифракция света на ДОЭ в ближней зоне Френеля исследовалась с помощью регистрации распределения интенсивности света ПЗС- камерой. Приемное окно камеры имело размеры 6.6 мм х 4.78 мм, число фотоячеек равно 768 х 567. Зарегистрированные картины дифракции запоминались в компьютере. Для исследования дифракции Фраунгофера на ДОЭ в пространство за элементом вводилась линза с фокусным расстоянием 500 мм.

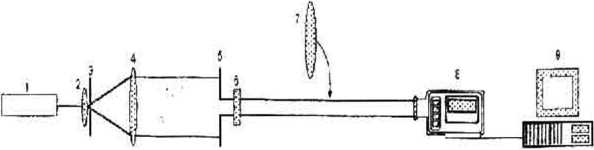
Рис. 3. Экспериментальная установка: He-Ne лазер (1), микрообъектив (2), фильтрующая диафрагма (3), коллимирующая линза (4), ограничивающая диафрагма (5), бинарный ДОЭ (6), добавочная линза для выполнения Фурье-преобразования (7), ПЗС-камера (8), компьютер (9)

На рис. 4-7 показаны результаты исследования для мод ГЭ с номерами (1,0), (1,1), (1,2) и (7.0), соответственно. На рис. 4а-7а показаны амплитудные бинарные фотошаблоны ДОЭ, ограниченные круглыми апертурами освещающего пучка с диаметром 1.2 мм. Фотошаблоны рассчитывались в соответствии с формулой (1). Однако, апертура была круглой и немного больше оптимального размера, что ухудшило результаты (в основном эффективность), которые могли быть получены в оптимальном случае (см. Таблицу 3).

На рис. 46-76 показаны рассчитанные по формуле (9) картины дифракции Фраунгофера на соответствующих фазовых бинарных ДОЭ.

■<

Рис. 4. Результаты моделирования и эксперимента для моды ГЭ (1,0): фотомаска, ограниченная круглой апертурой освещающего пучка (а); рассчитанная картина дифракции в дальней зоне (б); экспериментальная картина дифракции в дальней зоне (в) и ее трехмерное представление (г); экспериментальные распределения интенсивности на расстояниях 370 мм (д), 480 мм (е) и 620 мм (ж) от ДОЭ

Рис. 5. Результаты моделирования и эксперимента Для моды ГЭ (1Д); фотомаска, ограниченная круглой апертурой освещающего пучка (а); рассчитанная картина дифракции в дальней зоне (б); экспериментальная картина дифракции в дальней зоне (в) и ее трехмерное представление (г); экспериментальные распределения интенсивности на расстояниях 340 мм (д), 455 мм (е) и 640 мм (ж) от ДОЭ

Рис. 6 Результаты моделирования и эксперимента для моды ГЭ (1,2): фотомаска, ограниченная круглой апертурой освещающего пучка (а); рассчитанная картина дифракции в дальней зоне (б); экспериментальная картина дифракции в дальней зоне (в) и ее трехмерное представление (г); экспериментальные распределения интенсивности на расстояниях 260 мм (д), 400 мм (е) и 580 мм (ж) от ДОЭ

Рис. 7. Результаты моделирования и эксперимента д;ш моды 13 (7,0): фотомаска, ограниченная круглой апертурой освещающего пучка (а); рассчитанная картина дифракции в дальней зоне (б); экспериментальная картина дифракции в дальней зоне (в) и ее трехмерное представление (г); экспериментальные распределения интенсивности на расстояниях 360 мм (д) и 470 мм (ж) от ДОЭ.

На рис. 4в-7в показаны экспериментальные картины дифракции Фраунгофера (дальняя зона), которые были зарегистрированы в задней фокальной плоскости линзы с фокусным расстоянием 500

мм, дополнительно введенной в оптическую схему (рис. 3, позиция 3). На рис. 4г-7г показаны трехмерные представления экспериментальных картин дифракции Фраунгофера (рис. 4в-7в). Сравнивая рис. 46-76 и рис. 4в-7в, можно убедиться, что имеет место хорошее согласование теории и эксперимента.

На рис. 4д,е,ж-7д,е,ж показаны экспериментальные картины дифракции Френеля (ближняя зона) на разных расстояниях от ДОЭ. Из этих рисунков видно, что при распространении лазерный пучок проявляет модовые свойства - сохраняет свою структуру.

Таблица 3.

Рассчитанные средние ошибки и эффективность при формировании мод ГЭ с помощью бинарных знаковых ДОЭ с круглой апертурой немного больше оптимального размера

ТЕМ(т,л>	(М)	(1,П	(1’2)	(7,0)
8, %	24.7	42.7	31.5	64.2
Т], %	55.6	62.2	59.4	31.7

5.    Заключение

В работе получены следующие результаты.

• -    по технологии электронной литографии получены на кварцевом стекле бинарные ДОЭ для эффективного формирования отдельных мод Гаусса-Эрмита (1,0), (1,1), (1,2) и (7,0); функция пропускания таких ДОЭ равна знаковой функции от многочленов Эрмита;

• -    численное моделирование показало, что бинарные знаковые ДОЭ формируют первые моды ГЭ с эффективностью 64-72%;

• -    натурные эксперименты демонстрируют удовлетворительную работоспособность таких ДОЭ и согласие с теорией.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (№№ 96-15-96026, 98-01-00894).