Формирование модели выбора оптимального инвестиционного проекта по равновесию Нэша в рамках машиностроительного кластера

Теория игр имеет важную роль в экономике, и многие экономические явления моделируются как игры [1]. Есть много разных типов игр, и они могут отличаться по двум основным параметрам: игры могут различаться по количеству участников – например, игры с двумя или n игроками, и по тому, могут ли участвующие игроки достоверно выполнять набор действий, более известных как кооперативные и некооперативные игры [2]. Одна из основных проблем любой игры – это вычислить равновесие Нэша.

В рамках данной статьи мы использовали равновесие Нэша с целью построения эффективной инвестиционной стратегии в машиностроительном кластере [9]. Машиностроительный кластер представляет собой сеть из разных предприятий, которых объединяет одна общая цель – максимизация прибыли. Сформированная сеть между предприятиями, построенная с удовлетворением интересов предприятий, определяется целью развития инноваций и обмена знаниями [5]. В ряде примеров, предприятия, входящие в состав кластера, сокращают производственные издержки за счет кооперации, оптимизируют производственную цепочку поставок, снижают риски и повышают свой инновационный уровень [6].

В нашем случае игроки (предприятия) должны выбирать стратегии максимизации выигрыша в условиях сложной сети. В сетевой игре каждый агент рассматривается как участник некооперативной игры. Каждый игрок рационально выбирает стратегию, чтобы максимизировать функцию объекта (добиться максимального выигрыша). При этом все игроки могут достичь равновесия по Нэшу, при котором сеть достигает устойчивого состояния, и ни один игрок не может извлечь выгоду, отклонившись от своей оптимальной стратегии [13].

В этой статье мы представляем расширенную игру n игроков при неидеализированных условиях, а именно, когда игроки ограничены в ресурсах. В реальных социальных ситуациях фирмы не склонны инвестировать в своих союзников в соответствии с теоретическим решением неограниченного равновесия по Нэшу из-за финансовых, человеческих или других ограничений ресурсов [14]. Это означает, что фирмам необходимо изменить свои инвестиционные стратегии в зависимости от ресурсных ограничений, с которыми они сталкиваются.

Сотрудничество с другими фирмами может способствовать развитию инноваций в рамках кластера, но для формирования стратегических союзов требуются определенные инвестиции [15]. Требуемый уровень инвестиций зависит не только от самой фирмы, но также зависит от того, сколько предприятие-партнер планирует инвестировать – типичное игровое поведение. Нами расширена классическая игра делового партнерства для того, чтобы учесть различия в коэффициентах возврата их инвестиций.

Предположим, что два машиностроительных предприятия, №1 и №2, сотрудничают в совместном проекте. Предположим, что для того, чтобы этот проект был успешным, обе фирмы должны инвестировать, но сделав это, они делят любую прибыль поровну – своего рода беспроигрышные отношения. В классической партнерской игре коэффициент возврата инвестиций устанавливается равным 4. Устанавливаем этот параметр в своей партнерской игре. Мы устанавливаем этот параметр как переменную ã , дающую доход как уравнение (1)

I = y ( S 1 + S 2 + bS 1 S 2 ) (1)

S ₁ и S ₂ – это инвестиции обеих фирм соответственно. Пусть параметр b , известный как дополнительный коэффициент, не случайный и общеизвестный среди фирм. Кроме того, пусть дополнительный коэффициент будет ограничен значениями от 0 до 1/4, то есть пусть b e [ 0,1 / 4 ] .

Из уравнения (1) мы видим, что общий выигрыш, полученный двумя фирмами, зависит от стратегии обеих фирм S ₁ и S ₂ , а также от синергии, или кооперативного эффекта, определяемого bS ₁ S ₂ , который создается двумя работающими предприятиями вместе. В действительности фирмы имеют разные конкурентные преимущества и имеют опыт работы в разных проектах. Вот почему взаимные инвестиции и сотрудничество могут привести союзы к получению дополнительного дохода по сравнению с доходом, который они могли бы получить по отдельности. Предполагая, что доход I делится поровну между двумя фирмами и что инвестиционные затраты квадратичны по уровню инвестиций, выражения выигрыша P ₁ и P ₂ , соответствующие предприятию № 1 и № 2, задаются системой уравнений в (2).

P i = ¹ ■ y ( S + S 2 + bS i S 2 ) - S 12

- ² (2) P = 2 ■ y ( S i + S 2 + bS i S 2 ) - S 22

Учитывая свои функции выплат, компаниям необходимо выбрать оптимальные стратегии. Таким образом, чтобы стратегия любой фирмы была лучшим ответом на стратегию другой фирмы. Первой фирме необходимо найти лучшую стратегию реагирования на основе стратегии S ₂ , которую выбирает вторая фирма. Точно так же вторая фирма должна найти лучшую стратегию реагирования на основе стратегии S ₁ первой фирмы.

Чтобы найти наилучшие ответы для обеих фирм, давайте сначала вычислим частную производную первого порядка от P_i по S_i , получив

P = 2 ■ y ( 1 + bS j^ - 2 S i

Обнуляя производные в (3), Pi = 0 мы находим, что функция наилучшего отклика каждой фирмы опре- деляется выражением Si' = 1 ■ y■ (1 + bSj) - 2Si. Пусть BR, (Sj) обозначает наилучший ответ, который i при- нимает, когда j принимает стратегию Sj , тогда функции наилучшего отклика для 1 и 2 задаются формулой (4).

BR 1 ( s 2 ) = S 1 = ¹ ■ y - ( 1 + bS 2 )

⁴                             (4)

BR 2 ( S 1 ) = S 2 = -4 ■ y ' ( 1 + bS 1 )

Как видно из (4), если, у фирмы i нет ресурсов для достижения максимальной теоретической выплаты. С другой стороны, если S i >  ( 1 + bS j ) , фирма j может оказаться не в состоянии не увеличить свой уровень инвестиций S_j , и ресурсы, которые инвестировала фирма i, будут потрачены впустую. Это означает, что только если может уплотнить я добиться максимального выигрыша. Позволять обозначим равновесное решение по Нэшу, то мы легко можем проверить равновесие по Нэшу, заданное формулой (5).

S = S 2 =

Y

4 - y b

В этом состоянии ни одна фирма не может по- лучить выгоду, отклонившись от своей стратегии, учитывая стратегию другой фирмы и, следовательно, текущий набор стратегий. составляют равновесие по Нэшу.

Блок-схема расширенной игры для двух игроков показана на Рисунке 1.

Из этого результата мы видим, что, когда до- полнительный коэффициент b уменьшается, что оз- начает уменьшение отдачи от сотрудничества, выплаты будут уменьшаться для обеих сторон. Фирма, которая инвестирует больше, несет более высокие предельные издержки, но получает только половину предельной прибыли.

Увеличение коэффициента доходности ã имеет тот же эффект, что и увеличение коэффициента взаимодополняемости, поскольку увеличение доходности любой из фирм, участвующих в совместном про- екте, увеличивает уровень, с которым фирмы инвестируют в партнерство.

Далее рассмотрим расширенную сетевую игру n игроков в идеализированных условиях. В игре с n игроками есть определенное количество игроков, и мы будем использовать сеть, чтобы представить отношения между этими игроками. Пусть V = { 1,2,..., n } - множество узлов, а E = { e ij } ( i, j е V ) - множество ребер. Сеть можно рассматривать как неориентированный граф и представлять его как G = { V, E } . Множество V также является множеством игроков. Пусть e ij = { 0,1 } . Тогда e ij = 1 представляет собой ребро между узлами i и j. V ( i ) = {j | e ij = 1} показывает всех соседей, связанных с i, а количество прямых соседей называется степенью i, d i = |v ( i ) . В этой модели каждый узел представляет фирму. Фирма i использует стратегию X_i , где x_i , обозначает реализацию X_i , и является неотрицательным действительным числом. Прибыль фирмы i может быть представлена в виде вектора m i ( x i ,x V ( i ) ) , где x V ( i ) - вектор действий партнеров фирмы i. Как и прежде, выигрыш фирмы i зависит от действий ее партнеров и от ее собственных действий. Полагая d i = k, , вектор выплат фирмы i и вектор ее действий X_i , задаются уравнением (6).

k mi (Xi,x1,_,xk) = f(xi + A^xj) - c(xi)        (6)

j = 1

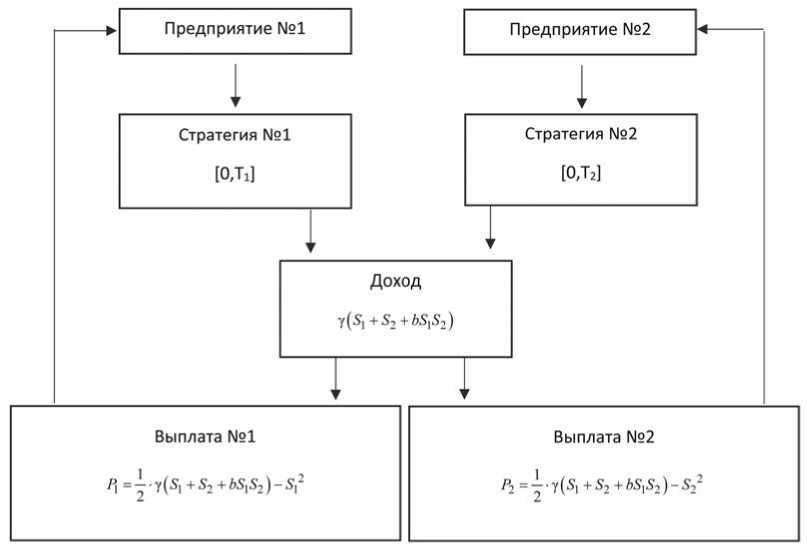
Рисунок 1. Блок-схема инвестиционного дохода двух фирм

В уравнении (6) пусть f ( • ) - неубывающая функция, а c ( • ) - функция затрат, связанная с инвестициями фирмы i. Параметр ц равен 1. Тогда сетевая игра полностью характеризуется ( G. X, m i ) .

Предположим, что в идеальных условиях каждая фирма имеет достаточно ресурсов и может полностью удовлетворить потребности своих партнеров. Эта сеть может достичь равновесия по Нэшу. Предположим, что фирма i и ее партнер j е V ( i ) могут достичь равновесия по Нэшу с неоднородными коэффициентами доходности ã_i j и дополнительными коэффициентами b ij . Как прежде, S ij* = ——   лучшая

4 - Yij bij инвестиционная стратегия в рамках каждого партнерства. Что касается фирмы Fi , обозначает равновесное решение по Нэшу между фирмой Fi и Fj. Следовательно, общий объем инвестиций Ri фирмы i определяется уравнением.

degree ( F i )

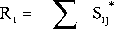
j = 1, j * i

degree ( F i ) z j = 1. j * i

Y j

^{4 -} Y ij b ij

Кроме того, выражение P i выигрыша дается формулой (8).

degree ( R i )

P. =  z Pj= j=1. j * i

degree ( R i )

j = 1. j * i

+ b ij S ij S ji ^)- S ij 2

Как показано на Рисунке 2, мы берем диаграмму сети инноваций. В качестве примера, и предприятия № 1-5 составляют полный граф из пяти элементов.

Давайте посмотрим на фирму № 1, степень d₁ которой равна 4. Предполагая, что коэффициенты доходности фирмы № 1 равны γ 12 ,…, γ 15, а коэффици-

енты дополнения равны b 12 ,…, b 15, мы можем рассчитать необходимые начальные вложения фирмы №1 R 1 = S₁₂ * + S₁₃ * + S₁₄ * + S₁₅ * и выигрыш P i = P₁₂ + P 13 + P₁₄ + P₁₅ при условии, что уровень начальных инвестиций является равновесным решением по Нэшу S₁₂*...S₁₅* .

Расширенная сетевая игра n игроков в неидеализированных условиях

В идеализированных условиях общие инвестиции R_i , которые фирма хотела бы инвестировать, представляют собой просто теоретическое значение, заданное равновесным решением по Нэшу, приведенным в (7). В действительности запасы ресурсов некоторых фирм не могут полностью соответствовать теоретическому R_i по разным причинам. Когда ресурсы фирмы i T_i не могут удовлетворить потребности партнеров в ресурсах в состоянии равновесия по Нэшу ( T i <  R i ), инвестиции фирмы в своих партнеров в соответствии с равновесием по Нэшу будут больше, чем ее собственные ресурсы. Такая ситуация называется нехваткой или ограничением ресурсов. Пусть степень нехватки ресурсов A i определяется, как в (9), а средняя нехватка ресурсов на градус 0 i , как в (10).

A . = Г - R i | (9)

0 i = A j I di (10)

В условиях нехватки ресурсов фирмы будут использовать разные стратегии, чтобы справиться с нехваткой ресурсов и контролировать общий уровень своих инвестиций. В процессе корректировки этих фирм их партнеры также будут корректировать свои стратегии, чтобы поддерживать наилучшие меры противодействия новому равновесию по Нэшу. Предположим, что две смежные фирмы i и j имеют начальные стратегии, заданные формулой S ij* = S ji* и что

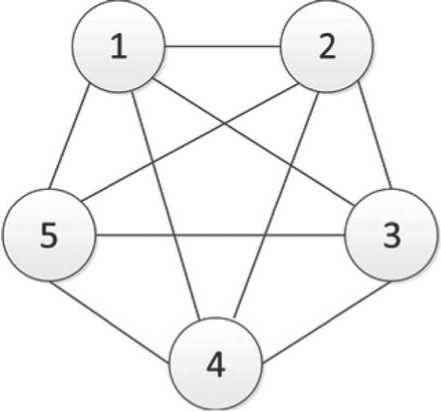
Рисунок 2. Сетевая диаграмма пяти предприятий

уровень ресурсов T каждой фирмы общеизвестен. Если фирма j меняет свою стратегию на новую инвестиционную стратегию S ji' из-за нехватки ресурсов, то, согласно уравнению (4), наилучшим ответом фирмы i с учетом новой стратегии является BR i ( S ji ' ) . Итак, для фирмы i требуемые общие инвестиции R i ' будут соответствующим образом скорректированы, как показано уравнением (11).

R i = R i - S ij* - BR i ( S ji) (11)

В рамках статьи мы предлагаем четыре инвестиционные стратегии, когда фирмы сталкиваются с нехваткой ресурсов, и с помощью моделирования реального машиностроительного кластера мы оцениваем результаты четырех стратегий, анализируя общие инвестиции, общую выплату, средний коэффициент доходности, степень среднего коэффициент возврата и оценку их общих преимуществ и недостатков.

Основываясь на приведенном выше анализе, в этой экспериментальной среде, в которой мы рассматриваем машиностроительные кластеры, мы можем сделать следующие выводы:

• 1.    Жадная стратегия – это наиболее подходящая стратегия распределения ресурсов для достижения максимальной отдачи для всего кластера. Это всегда приносит максимальную отдачу сети кластера. На втором месте – эффективность пропорциональной стратегии, которая также хорошо себя зарекомендовала. Эту стратегию также стоит учитывать при принятии решений о распределении. Хотя эффективность средней стратегии лучше, чем случайной стратегии, средняя стратегия все же хуже, чем первые две стратегии, и поэтому не рекомендуется.

• 2.    Когда общие инвестиции кластера имеют фиксированное значение или, что более важно, общий доход альянса является фиксированным значением, нам необходимо выбрать подходящую стратегию в соответствии с нормой прибыли. Если общая сумма инвестиций кластера является фиксированной, тогда выбор жадной стратегии, которая имеет наивысшую норму прибыли, может принести кластеру более высокие выплаты. Если общий доход альянса является фиксированным значением, то выбор жадной страте-

• гии, которая имеет наивысшую норму прибыли, может помочь свести общие инвестиции альянса к минимуму, чтобы у альянса было больше ресурсов, доступных для удовлетворения других потребностей.

• 3.    Чем больше партнеров имеет фирма, тем более высокийстатус получаетфирма. Нотем большеона должна инвестировать в кластер. Независимо от того, какая стратегия выбрана, фирмы с более высоким статусом всегда могут получить более высокую прибыль.

• 4.    Независимо от того, какая стратегия выбрана, фирмы с более высоким статусом всегда будут получать более низкую норму прибыли. Это связано с тем, что чем больше у фирмы партнерских отношений, тем выше затраты фирмы-инвестора, например, на поддержание партнерства. Следовательно, норма прибыли невысока. Однако для бизнеса достижение максимальной нормы прибыли, возможно, не обязательно, поскольку более важна более высокая отдача.

С точки зрения практического значения, средняя стратегия не так хороша, как пропорциональная стратегия или жадная стратегия. Последние два имеют более высокую тенденцию к максимизации выгоды, чем средняя стратегия. Жадная стратегия всегда направлена на выделение средств на проект с наивысшим коэффициентом доходности и соответственно сокращает инвестиции, чтобы получить наивысшую норму прибыли. Пропорциональная стратегия сохраняет те же отношения распределения, что и неограниченное равновесие по Нэшу, но она распределяет меньше партнерам с высокой доходностью, чем жадная стратегия. Таким образом, отдача от пропорциональной стратегии ниже, чем от жадной.

Для возможной будущей работы следует отметить, что хотя экспериментальная среда основана на примере машиностроительного кластера, некоторые параметры генерируются случайным образом. Таким образом, выводы, представленные в этой статье, могут быть применимы не для всех случаев. Кроме того, в партнерской игре между компаниями все еще есть много дополнительных факторов, которые необходимо учитывать, и эта модель дает только определенные экспериментальные выводы в нескольких теоретических экстремальных ситуациях, чтобы предложить теоретические основания для решений компаний о распределении.