Формирование номинальной программы управления космическим аппаратом с двигателями малой тяги при перелете между эллиптической и геостационарной орбитами

Для построения номинальных программ управления исследователями использовались методы теории оптимального управления, прежде всего принцип максимума Понтрягина, для систем точных или усредненных уравнений движения. Построение усредненных уравнений во многих случаях позволяет упростить поиск оптимального управления, а иногда получить аналитическое решение задачи, что является очень важным для формирования номинальных программ управления движением.

Так, в [1] для случая, когда вектор тяги располагается в плоскости местного горизонта, получены оптимальные зависимости угла отклонения вектора тяги от плоскости орбиты для перелетов между круговыми некомпланарными орбитами. Для монотонного изменения наклонения в моменты, когда аргумент широты u = ±п 1 2 , направление тяги меняется на симметричное. Позднее было получено оптимальное управление углом на витке для околокруговых орбит и оптимальные по быстродействию структуры совместного управления элементами (А, е, ω ) и ( Ω , i) эллиптической орбиты трансверсальным и бинормальным реактивным ускорением в пределах витка соответственно [2].

Совместное изменение большой полуоси, эксцентриситета и наклонения при перелете с эллиптической орбиты на ГСО подробно рассмотрено в [3]. В этой работе показано, что угол отклонения вектора тяги от плоскости орбиты на витке меняется по закону, близкому к релейному. Структура ориентации вектора тяги в плоскости орбиты также содержит разгонные и тор-

мозные участки или в частном случае только разгонный или тормозной участки.

В [2] приведены аналитические зависимости изменения большой полуоси и эксцентриситета при условии постоянства ширины активных и пассивных участков, что облегчает решение основной проблемы оптимизации [1] — найти такое управление тягой и выбрать такие значения параметров двигательной установки, которые позволяют выполнить заданный маневр за фиксированное время, обеспечивая максимум полезной нагрузки.

В данной работе рассматривается задача формирования номинальной программы управления космическим аппаратом (КА) с двигателями малой тяги (ДМТ) при перелете между эллиптической и геостационарной (ГСО) орбитами.

Эта задача возникает при оптимизации выведения полезной нагрузки на ГСО с последовательным использованием разгонных блоков с двигателями большой тяги (ДБТ) и ДМТ. Во многих работах было показано, что оптимальной является схема перелета через эллиптическую орбиту, сформированную после первого разгонного импульса ступени с ДБТ. Как показывают расчеты, эксцентриситет такой орбиты составит величину от 0,6…0,7, а радиус апогея 50000…150000 км.

Для перехода с такой орбиты на ГСО необходимо изменить как минимум три элемента орбиты: большую полуось, эксцентриситет, наклонение. Последовательное изменение этих элементов по сравнению с совместным изменением, как показывают расчеты, приводит к большим затратам характеристической скорости. В данной работе предлагается схема совместного изменения указанных элементов в рамках простых схем управления вектором тяги на витке в плоскости местного горизонта:

v = [ v -V 2 + ( v 1 + v 2 ) sign (cos( и )) ] • 0,5 . (1)

Здесь n , V 1 , V ₂ - углы отклонения вектора тяги ДУ от плоскости орбиты, u – аргумент широты.

Примем, что возмущения от несферичности Земли, атмосферы и других факторов отсутствуют, оси апсид начальной и конечной орбит совпадают с линиями узлов и лежат в плоскости экватора ( ГО ₀ = 0 и и = ^ ). Используя замену

ц - гравитационная постоянная.

Выражение (1) примет вид:

v =

V 1 - V 2 + ( V 1 + V 2 ) sign (

cos E - e

1 - e • cos E

)

• 0,5. (3)

Моменты изменения ориентации тяги и = ± n / 2 соответствуют эксцентрической аномалии точек переключения E_пер :

— = Е (1 — e •cos E Г dt А 3

перейдем в дифференци-

E „ _ep = arccos( e ) = arcsin V1 - e ² .    (4)

После усреднения на витке получим:

альных уравнениях движения [4] к новой независимой переменной – эксцентрической аномалии Е :

dA

dE n

ц

dA dE

2 • a • cos( v ) • — • V1 - ee ц

^ 2 • arccos( e ) • (cos у - cos v ₂) +) x l                                                                  I,

^+ 2 • n • cos v ₂                  J

de           A ²

= a • cos(v)•    • У1 -e "(2• cosE-e• cos E-e dE ’ ц v                       '

de

dE 2 n

di

di            A ²

— = a • sin( v )--- dE

cos E • (1 + e ² ) - e • cos ² E - e

^ [ cos у

ц

1 - cos v ₂ ] x

Ц

d Q

— = a • dE dro

sin( v ) A ²

•     • (sin E sin i ц

1 A ²

71-7

- ₂ e • sin 2 E ),

,

X

X

e ²

,

di

- 3 • n • e • cos v ₂

- 1

A ²

J

— = ax dE e ц

| cos(v) • (1 -e2)sinE +| xl

(+ sin E • (1 - e • cos E ) • (cos( v ) - e • sin( v ) • ctgi) J

— =-- a--, x dE 2 п   ц. -K-e

I [ sin v + sin v l • l (2 + e ²)V1 - e ² - 3 - e • arccos( e ) l +| _z__x xr ^{1      2}                                   L (5)

^+ 3 • n • e • sin v ₂                                      J

dV      A ³

-— = a •     -⁽1 ^- e • cos E )

dE у ц

где А, e, i, Q, ro, и - элементы орбиты; V x - характеристическая скорость; а – модуль ускорения;

dQ=0, dE dro dE

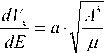
Vl. KTd/C

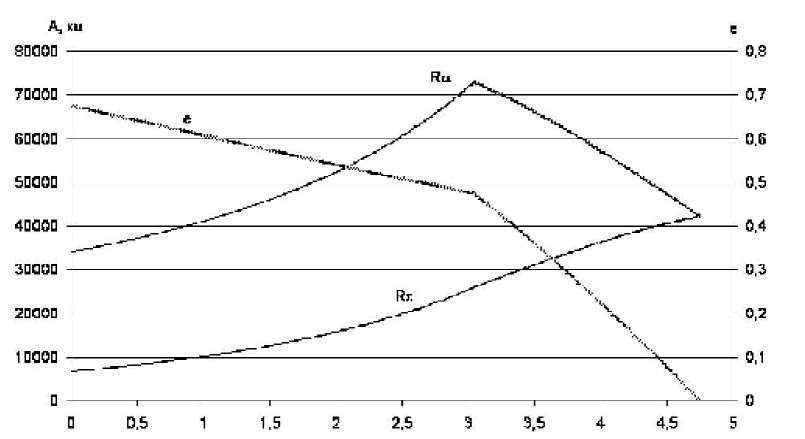
Рис. 1. Зависимости радиусов перигея R_p , апогея R_a , эксцентриситета е от затрат характеристической скорости V_x

Согласно (5) аргумент перицентра w и восходящего узла W остаются постоянными. Система не зависит от эксцентрической аномалии и может быть уменьшена на три уравнения. Перейдем к новой независимой переменной V_x :

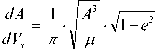
х (2 ■ arccos( e ) ■ (cos v 1 - cos v ₂) + 2 ■ n ■ cos v ₂),

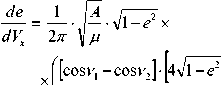
- 3 ■ n-e ■ cos v ₂

di -1 I A dVx ~ 2п Vц(1 -e2)

| [ sin r ₁ + sin v ₂ ] ■ (+ 3 ■ л-e ■ sin v ₂

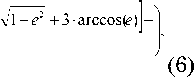
■ e ■ arccos e ) ] +)

,

Основываясь на анализе возможных структур управления, сформируем простое для технической реализации управление:

V, = const, 0 < V < V,, 1                       x xк fo 0

К у

,    ' x пер — ' x — ' xк *

Здесь V_xк – конечная характеристическая скорость, V_{x пер} – характеристическая скорость, начиная с которой разгонный участок в перигее заменяется на тормозной.

Граничные условия перелета между произвольной эллиптической орбитой и ГСО запишем в виде:

Vx =⁰ : A = A 0, e = e 0, i = i 0,

V = V : A = 42160км, e = 0, i = 0 .    ⁽⁸⁾

x xк

Решим краевую задачу для перелета КА начальной массы 780 кг с начальной орбиты, имеющей радиус перигея 6595 км, радиус апогея 34000 км, наклонение 63,17° и нулевые аргумент перигея и долготу восходящего узла. Тяга ЭРД КА принимается равной 0,166 Н, удельный импульс 1500с [3].

В результате решения краевой задачи наилучшее решение

A_K = 42170,03 км, е _к = 6 -10^-6, i_K = 0°,

Vx = 4,75 км / с достигнуто при n1=61,26°, Vx пер=3,04 км/с.

Для оценки ошибок усреднения проводилось интегрирование системы (2) с управлением (7). Интегрирование останавливалось по условию V_x = 4,75км / с . При этом элементы орбиты достигают следующих значений:

A = 42037,23 км, е, = 0,0015, i = 0,01° . к    кк

Максимальная ошибка по большой полуоси составляет около 130 км, что не превышает 0,3%

Зависимости радиусов перигея R_p , апогея R_a, эксцентриситета е, наклонения i и программы управления от затрат характеристической скорости V_x приведены на рис. 1 и 2.

Анализируя рис. 1, на графиках зависимостей радиусов апогея, перигея и эксцентриситета можно выделить по два характерных участка: изломы у радиуса апогея и эксцентриситета, перегиб у радиуса перигея соответствуют изменению направления тяги в перигее на противоположное. Эксцентриситет меняется по зависимостям, весьма близким к

Рис. 2. Зависимости наклонения i и углов отклонения вектора тяги от плоскости орбиты v1,v₂ от затрат характеристической скорости V_x

S

линейным, с характерным переломом. Радиус апогея возрастает до значения 73 тыс. км, что объясняется более эффективным изменением наклонения на большем удалении от притягивающего центра.

На рис. 2 можно отметить, что наклонение до момента переключения V_{x пер} меняется по линейной зависимости, в дальнейшем изменение наклонения уменьшается и принимает нелинейный характер.

Таким образом, можно сделать вывод, что сформированная номинальная программа обладает простотой, что позволит осуществить техническую реализацию управления с контуром обратной связи.