Формирование оценочных функций для решения задачи построения направленной динамической байесовской сети

Вероятностные модели являются достаточно хорошо апробированным инструментом для моделирования сложных стохастических процессов, в том числе имеющих переходные состояния во времени. Набольший интерес представляют вероятностные модели байесовских сетей (далее – БС), позволяющие определить вероятностные связи между узлами путем задания таблиц условных вероятностей.

Процедура получения направленной структуры требует формализации существующих подходов к обучению и определению тех оценочных функций, которые наиболее применимы для решения определенной практической задачи. Применение оценочных функций в процессе обучения тесно связано с операциями добавления, удаления и изменения направленности связей между ребрами. Для каждой из операций рассчитывается значение оценки, характеризующей вес каждого ребра, после чего выбирается значение

Полухин Павел Валерьевич кандидат технических наук, преподаватель кафедры математических методов исследования операций, Воронежский государственный университет, город Воронеж. Сфера научных интересов: машинное обучение, статистический и системный анализ данных, математическое и компьютерное моделирование, программные комплексы. Автор более 30 опубликованных научных работ.

оценки, имеющей максимальный вес. Процедура поиска экстремума оценочной функции направлена на получение корректной структуры графа БС с максимальными весами и на установление зависимости весов ребер графа от обучающей выборки, поступающей на вход данного алгоритма. Применение различных алгоритмов поиска минимаксного значения оценок обусловлено реализацией задачи повышения точности за счет исключения образования локальных оптимумов и как следствие получения некорректной структуры вероятностной сети.

Процедура формирования оценочных функций

Для задания оценочных функций предварительно определим семантику БС, представляющей собой граф G = ( X , E ) , где X = ( X 1 , X 2, . , X n ) - переменные, характеризующие узлы байесовской сети; D i = ( D 1 ¹, D 2¹,..., D ni ) - домен значений, который могут принимать переменные X_i . Каждой из переменных X соответствует условное распределение

P ( X | Parents ( X ) ) , формируемое с учетом присутствия родительских вершин Parents ( X ) . Если для вершины X отсутствуют родительские вершины, распределение P ( X ) = P ( X | Parents ( X ) ) будет являться безусловным. Полное совместное распределение БС будет иметь вид [1; 2] n

P ( X 1 , X 2,... X n ) = П P ( X i Parents ( X i ) ) • (1)

i = 1

Из общей формулировки БС следует, что процедура обучения структурно делится на два основных этапа: обучение структуры и параметров. Рассмотрим более детально обучение структуры сети и связанную с ней процедуру формирования определенных типов оценочных функций, участвующих в получении результирующей оценки каждой из дуг графа, и формирование БС с максимальным значением правдоподобия структуры. В этом случае задача поиска оптимальной структуры сводится к решению следующей экстремальной задачи:

G = argmax f ( G , D ) . (2)

Определим основные оценочные функции, применяемые в процессе решения задачи обучения структуры БС. Для формирования оценочных функций введем понятие локальной и глобальной условной независимости родительских вершин переменной X :

qi

P ( ® i^G G ) = П P ( ® i^i G ) ,

j = 1

Формирование оценочных функций для решения задачи построения направленной ...

где 0G =  0GGj - значения параметров для переменной Xi с учетом родительских вершин j=1

Parents ( X . ) для графа G .

На основании свойства условной независимости 0 . можно определить распределение Дирихле следующего вида [3]:

n q. A yr а     ri         „ , р (0 g g ■ НИ. f1. n(0g. k Г■             (4)

■=1 ^j = 1 П k = 1 ^{A ( а ,} j ^, k ^{) k} = 1

С учетом распределения Дирихле можно определить метрику Байеса – Дирихле следующего вида [4]:

n q .     Г ( У r a .js ) r _r N.. + а 1

bd = yy iu^-=k=-^L + У _L jj ) ,

«Г ( У r = 1 N , j.. +^, ) -     ^{Г (} а j . ■ )                    (5)

а.,j,к = a ( xi = k, P ( xi ) = j ) =     , r q где a.,j,k - параметр распределения Дирихле; r. - домен всех возможных значений для родительских вершин Parents(X.); q. - произведение по всем r.; Г(.) - гамма-функция.

Частным случаем оценки Байса – Дирихле является метрика K 2, формируемая из выражения (5) при а . , j , _k = 1 [5]:

n q-          ( r - 1 ) !          ^r

K ² = ln ^P ( ^G ) 11 ln     '       + У ln ⁽ N . , j , s ^!) .                   (6)

и # ( N . , j ⁺ r . ^{- 1} ) ^! 7=1

В реальных условиях вычисление параметра а . , j , к сопряжено со сложностями, в связи с этим необходимо установить его зависимость от размера эквивалентной выборки, определяемой для БС с учетом ее семантики:

а.,j,к = N® (xW",xn ), где а(x1,^,xn) - вероятность, соответствующая априорной структуре БС.

Вероятность P ( X|G ) с учетом положительной меры { 1, ^ , r ₁ } x_x { 1, _ , r_n } можно задать в следующем виде:

а( x1,^, xn )=     n .

H. 1 r

Перепишем параметр Дирихле (8) в виде а., j, к = а (x. =к. P (x. )=j )=—.

r q

Из выражения (5) с учетом (9) получим математическое описание эквивалентной метрики Байеса – Дирихле [6]:

BDe =

q

11 "

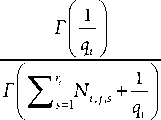
Наряду с метриками, построенными на основе метрики Байеса – Дирихле, рассмотрим формирование оценочных функций, реализованных на основе логарифма правдоподобия и взаимной информации. Оценочную функцию на основе логарифма правдоподобия можно записать в виде n qi ri

L (G ,0G, D )=111Ni, j, kl"-j.

i = 1 j = 1 k = 1

Чтобы определить критерии Шварца и Акаике, получаемые из выражения логарифма правдоподобия, найдем общее число параметров БС по формуле [7]

m=1 (ri -1) q.

Метрику минимальной длины описания (далее – МДО) получим из выражений (11) и (12):

n qi ri f ( M ) = E11Ni, j, " N   - 1MIn ( N ).

i = 1 j = 1 k = 1             N i , j ¹

Альтернативным подходом для формирования оценок структуры БС является использование теории информации. Данный подход позволяет получить наиболее качественную оценку структуры с учетом имеющейся обучающей выборки. Обобщая выражение (13), можно получить выражение для оценок Шварца и Акаике следующего вида:

n qi ri

Q ( m )=11 INijk" -j- - MF(N ).

i=1 j =1 k=1

Из выражения (14) при F ( N ) = 1 имеем метрику Акаике, F ( N ) = In ( N ) /2 - критерий Шварца.

Формулировку логарифма правдоподобия можно определить также на основе условной энтропии H ( X ) , устанавливающей связь между дочерней вершиной X i и ее родительскими вершинами [8]:

L ( G , 0 ^G , D ) = - N j^ H ( X i parents ( X i ) ) = - NH ( G ) , i = 1

r "

n

H ( G ) = 1 11 P ( x i Parents ( X i ) ) ^x l" 11 P ( x i parents ( X i ) )

x ^ i = 1

V i = 1

Vy

где H ( G ) - значение энтропии графа байесовской сети G .

Из выражения (15) следует, что оценки, построенные на основе логарифма правдоподобия, минимизируют значение условной энтропии для каждого из параметров БС с учетом всех родительских вершин. Это дает возможность найти те значения родителей, кото- рые вносят больше информации относительно интересующей вершины Xi . Наряду с условной энтропией сформулируем оценку на основе взаимной информации. Для этого

Формирование оценочных функций для решения задачи построения направленной ...

определим распределение для всех переменных сети графа P g ( X ) и распределение, соответствующее обучающей выборке D для параметров 9^е с учетом семантики БС:

P g ( X ) = № ( X i i Parents ( X i ) ) '                           (16)

i = 1

Тогда для распределений Pd (X) и Pd (X) можно определить выражение для расчета дистанции Кульбака – Лейблера как [9]

d kl =e P g ( X ) ln P^ .                     (17)

Используя формулировку энтропии H ( X ) , выражение (17) для расстояния Кульбака

– Лейблера перепишем в следующем виде:

nn dkl=- Hd (X )+EHd (Xi )+EHd (y)-Hd (Xi), i=1                i=1                                                    (18)

Yi = Xi и Parents( Xi), где Hd (X) - энтропия для параметров X с учетом имеющейся обучающей выборки d с D.

Определим взаимную информацию для двух распределений параметров X и

Z е Parents ( X ) :

P ( X I Z )

X          ^P ( X ) ^P ( Z ) .

Используя энтропию H ( X ) и H ( Z ) , можно переписать выражение (19) в терминах энтропии Шеннона:

MI ( X , Y ) = H ( X ) + H ( X и Z ) .

Отметим, что последовательное добавление переменных в оценку на основе взаимной информации приводит к ее постепенному росту в соответствии с неравенством

MI ( X, X и Parent 1 ( X ), Parent 2 ( X ))> MI ( X, X U Parent 1 ( X )) .

Установим связь между взаимной информацией MI ( X , Z ) и оценкой правдоподобия (11):

n 1 n

EMI(Xi,Parent(Xi ))= L(G,9G,D) + EH(Xi).

i=1

Тогда, максимизируя оценку логарифма правдоподобия, получим следующее выражение:

nnq i r i

EMI(Xi,Parent(Xi )) = NNEEENi,j,klnNnNk"..

i = 1                                               i = 1 j = 1 k = 1                  i , ^k i , j

Отметим, что аналогичным образом можно получить выражение для оценки условной взаимной информации при наличии переменных X , Z и V :

MI ( X , Z I V ) = Y p ( Z ) Y p ( X , Z I V ) ln— ^{P ( X} , Z | V ) —. M E X      Z^      \ ⁵ P ( X I V ) P ( Z I V )

Рассмотрим процедуру применения оценки на основе взаимной информации применительно к структуре динамической байесовской сети (далее – ДБС). Рассмотрим струк- туру двухслойной ДБС с множеством обучающих данных для двух временных срезов D0 и D1 . Тогда значение логарифма правдоподобия для графа, характеризующего начальный срез ДБС, можно определить с учетом выражения (11) следующим образом:

n r i

L о ( G о , ^ ^{5 о} , D о ) = ЕЕ ^N k ln^ .                      (25)

* = 1 ¹ = 1         N /

Аналогично получим оценку логарифма правдоподобия L 1 ( G 1 , p 1 , D 1 ) для графа G 1 с учетом обучающей выборки D ₁ . Тогда искомая оценка взаимной информации, соответствующая графам из двух смежных временных срезов, будет иметь вид

Е MI ( X * , Parent ( X * ) ) = ^A L ,

i = 1

A L = L ( G^ , D 1 ) - L о ( G о ^ 0 , D о ) .

Выражая разность оценок для двух срезов на основе взаимной информации, получим выражение для расчета A Q ( M ) [10]:

A Q ( M ) = ( ( L i ( G_v 9 ^G1, D i ) - M 1 F ( N ) ) - ( L о ( G о , ^ 0 , D о ) - M о F ( N ) ) ) =

1 ⁿⁿ

= 2 Е NMI ( X* , Parent ( X* ) ) — Е ( r ^X q — 1 ) .

Из выражения (27) следует, что мы можем получить универсальную оценку для метрик Шварца, Акаике и логарифм правдоподобия для двух смежных временных срезов с учетом взаимной информации между данными срезами. Отметим, что взаимная информация между вершинами, имеющими связи между срезами, формируется с учетом роди- тельских вершин Parent (X*) из начального среза на основе анализа обучающих выборок D0 и D1 . Чем больше значение метрики, тем больше вес ребра между родительской и дочерней вершинами двухслойной ДБС.

Для оценки достоверности получаемой структуры на основе вычисления метрик Байеса – Дирихле, логарифма правдоподобия, Шварца и Акаике воспользуемся вычислением максимума перекрестной энтропии (далее – МПЭ). Сформулируем МПЭ для двух графов ДБС, соответствующих срезам:

P ( H _о ( X _о, Parents ( X 1 ) ) |D _о ) <  P ( H 1 ( X 1 , Parents ( X 1 ) ) |D 1 ) .             (28)

Рассмотрим МПЭ применительно к семантике БС на основе подхода, предложенного ранее в работах Сузуки:

H о ( X * |, p * , j | k ) < H 1 ( X * | Y , p * , j | k ) , Y ' c Y " c Parents ( X * ) ,

p * , j | ^k

^a *jk + ^N *jk « *j ^{+ N} *j ’

BD ( X * | Y , a * ) > BD ( X * | Y , a * ) .

С ростом размерности обучающих выборок D ₀ и D ₁ устанавливаем сходимость p _{, j} | _k к a j _k . Тогда имеем

H о ( X * | Y , a *jk ) < H 1 ( X * | Y a jk ) , Y c Y ‘ .                             (30)

Формирование оценочных функций для решения задачи построения направленной ...

Заключение

Рассмотренные в работе процедуры формирования оценочных функций напрямую влияют на качество обучения структуры БС и ДБС. Применение различных оценочных метрик позволяет адаптировать процедуру обучения для решения конкретной практической задачи и определить ту метрику, которая позволяет получить наиболее правдоподобную структуру. Метрики Шварца и Акаике являются развитием логарифма правдоподобия за счет внесения дополнительной информации относительно родительских вершин, а также корректировки оценки с учетом размера данных N . В то же время метрики на основе условной и взаимной информации доказывают свою состоятельность применительно к семантике двухслойных моделей ДБС и достаточно просто могут быть выражены через оценку логарифма правдоподобия L ( G , 0^G , D ) . Применение оценок для ДБС позволяет установить факт изменения оценок для каждого из временных срезов, что особенно проявляется для переменных, имеющих транзитивные связи между вершинами. В этом случае общая оценка представляет собой разностную меру оценок для каждого из графов G ₀ и G ₁ . В процессе обучения БС и ДБС данные метрики могут быть использованы в алгоритмах восхождения к вершине, имитации отжига для поиска максимума оценки в результате процедуры добавления, удаления или изменения направленности графа сети. В этом случае вычисление метрики может выполняться рекурсивно для каждой переменной X сети после формирования узлов-кандидатов в родительские вершины Parent ( X ) . В случае ДБС в состав узлов-кандидатов попадают родительские вершины из предыдущего временного среза Parents ( X 0 ) , а формирование оценок происходит с учетом обоих наборов обучающих данных D ₀ и D ₁ .

Другой затронутой темой исследования является оценка достоверности структуры БС и ДБС. Применение оценки МПЭ позволяет определить тот граф сети, который в наибольшей степени отражает все параметры обучающих выборок D ₀ и D ₁ для двух срезов ДБС. Двухслойная модель ДБС может быть представлена в виде набора статических БС, связанных между собой ребрами. В результате МПЭ позволяет оценить наиболее согласованную структуру, где каждая дуга графа имеет правильную направленность, обусловливающую вероятностную семантику БС для каждой из вершин с учетом множества родителей.