Формирование оптического сигнала, согласованного со сфероидальными функциями, для передачи в линзовой системе без искажений

Понятие коммуникационных мод [1] широко изучается и применяется в оптике на протяжении нескольких последних десятилетий [25]. Вытянутые угловые сфероидальные функции, которые образуют коммуникационные моды для квадратных апертур и преобразования Френеля, также хорошо известны и были изучены аналитически в 60-х годах прошлого столетия [4, 6, 7].

Сфероидальные функции представляют собой полный набор функций с ограниченной спектральной полосой, которые ортогональны как на данном конечном интервале, так и на бесконечном интервале [6]. Суперпозиция данных функций, аппроксимирующая некоторое световое распределение, будет обладать инвариантным характером при прохождении через оптические линзовые системы с ограниченной апертурой.

В данной работе за основное интегральное преобразование принимается преобразование Фурье. Рассматривается разложение оптических сигналов по сфероидальным функциям, оцениваются погрешности аппроксимации, а также осуществляется применение оператора распространения к исходным полям и их аппроксимации. Демонстрируются инвариантные свойства оптического сигнала, согласованного с суперпозицией сфероидальных функций.

• 2.    ПРИМЕНЕНИЕ СФЕРОИДАЛЬНЫХ ФУНКЦИЙ ДЛЯ ЗАДАЧИ ДИФРАКЦИИ

Рассмотрим монохроматическое скалярное поле, полученное в результате дифракции световой волны на отверстии в плоском экране (рис. 1) [8].

Для плоского распределения вторичных источников значение поля в наблюдаемой точке может быть записано как:

U ( Г) = J G ( r , p > ) U „ ( p ) d ² p,      (1)

A где U0(r) - значение поля на апертуре A (на рис. 1), r = (x,y,z) - наблюдаемая точка, P = ( Px , Py ,0) — координаты апертуры, U(r) - значение поля в точке Г ,

• ^r 1 ^d exp⁽ ik | ^r — p I)

G ⁽ r , p ) =-—- --———--^- функция

2п dz     | r - p |

Грина описанной системы [9], k – волновое число.

После помещения апертуры в начало координат третья координата на ней обращается в ноль. Обозначим также наблюдаемую область O

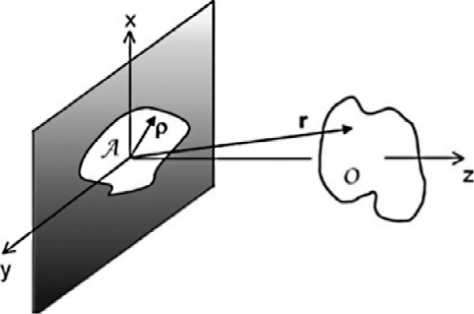
Рис. 1. Изображение геометрии системы и потребуем, чтобы она не перекрывалась с апертурой A . Разница между различными зонами дифракции определяется аппроксимацией функции Грина.

В дальнейшем будем рассматривать только физически реализуемые поля, т.е. такие поля, у которых амплитуды являются интегрируемыми в квадрате. В этом случае мы можем определить гильбертово пространство Н A .

Для задания гильбертова пространства определим скалярное произведение следующим образом:

^(U 0J , U 02 ) Н A = f ^U 01 ^{( р ) U} 0*2 ⁽ P ) d 2 ^p , (2)

A где U01, U02 - два исходных поля на апертуре, а звёздочкой обозначено комплексное сопряжение.

Комплексные амплитуды поля на апертуре будем рассматривать как вектора гильбертова пространства.

Аналогичным образом мы можем определить гильбертово пространство Н O амплитуд поля в рассматриваемой области O на рис. 1. Далее, введём оператор Г : Н A ^ Н O , который преобразует поле на апертуре A в поле на рассматриваемой области O . Другими словами, оператор переводит вектор из пространства Н A в пространство Н O :

U = Г U 0 ,             (3)

где Г определён как интеграл в выражении (1), U ₀ - исходное поле на апертуре, вектор-функция, U – поле в рассматриваемой области, вектор-функция.

Если задать апертуру и рассматриваемые области ограниченными и непересекающимися, то можно показать, что оператор Г является оператором Гильберта-Шмидта [10, 11], что говорит о существовании множества нормированных функций, являющихся решением задачи собственных значений и собственных функций

Г * ГТ = 1g I2 т n nn и другого множества нормированных собственных функций

ГГ * ф . = | g n |’ ф , .            (5)

где Т n и Ф n - собственные функции соответствующих операторов из уравнений (4) и (5), |g n | - собственные значения, Г * — оператор, сопряжённый к оператору Г .

Причём функции Т n и Ф n связаны следующими соотношениями [12]:

ГТ n = g n Ф n ;            (6)

Г * Ф = g * Т .          (7)

n nn

Можно показать, что множества { Т n } и

{ Ф n } являются полным базисом в пространствах Н A и Н O соответственно. Поэтому поле на апертуре можно представить следующим образом:

to

U 0 ^{( р} ) = Z a n ^Т n ^{( р} ) ,        (8)

n =0

где a n – это комплексные коэффициенты. Из (3) и (6), очевидно, следует, что результирующее поле в рассматриваемой области:

to

^{U ( r)} = £ a n g n ^Ф n ^{( r)} ,         (9)

n =0

Из последней формулы видно, что стоит лишь систему однажды определить, и задача о распространении поля становится несложной.

В случае параксиального распространения световой волны функция Грина имеет следующий вид:

- -X      k k

G ⁽ r , P ) ~   .   ^- i- ⁽ xPx + yp, )

2 nzz    z

Если предположить, что по оси y нет никаких изменений всех связанных величин, то мы имеет одномерный случай, где функция Грина запишется следующим образом:

x k f .k 1

G ⁽ x , P x ) = J ^ . ^exp|    i-xP x I . (11)

V 2nzzv

Тогда найдём оператор Г * Г :

Г * Г U ₀( x ') =

р

x 0

x 0

k ,0 xYk

= Ji J exP i_ px(x'-x) dPx iU o(x)dx ,(12) 2nzz

P x 0

- x 0

-

где x ₀ - половина ширины рассматриваемой одномерной области, p x 0 - половина ширины одномерной апертуры.

Возьмём внутренний интеграл в правой части и в качестве U ₀ ( x ) возьмём собственные функции:

| g n l ^{2 U} 0 n ⁽ x ')

^x 0

f

k sm z Px0(x'-x)

n ( x '- x )

U 0 n ( x ) dx , (13)

где U _{0 n} ( x ) - соответствующая собственному значению g n собственная функция. Полученное соотношение показывает, что данные собственные функции являются сфероидальными.

Собственные значения g n имеют следующее поведение: они приблизительно равны единице до некоторого критического значения

2 х_йкр

N = — 0 их 0

п

а затем все g n приблизительно

равны нулю [4].

Это число определяет количество сфероидальных функций – так называемых коммуникационных мод – по которым можно раскладывать произвольные оптические сигналы. Оно зависит от длины волны и геометрии системы и является числом степеней свободы системы.

С помощью формулы (13) можно найти модули g n , а аргументы вычисляются по следующей формуле:

у . _т ( х , у ) можно рассматривать как произведение двух одномерных сфероидальных функций:

У .т ( ^х, У ) = У . ( ^х ^ Ут ( У )'        (¹⁷⁾

Собственные значения в этом случае запишутся следующим образом:

|g.m | = | g .|| g m | .                  (¹⁸)

3. МОДЕЛИРОВАНИЕ ПРОХОЖДЕНИЯ СИГНАЛА И ЕГО СУПЕРПОЗИЦИИ

arg g_n

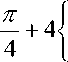
4 I 2 ’

n +11 п

где { } в данном случае - дробная часть от числа.

Разложение (8) одномерного оптического сигнала по сфероидальным функциям записывается в следующем виде:

Произведём расчёт сфероидальных функций, согласованных с параметрами оптической системы, состоящей из двух линз, и выполним разложения по ним оптического сигнала.

В качестве примера рассматривается случай, когда kPx ₀ / z = ²⁰ , х 0 = 1, а исходный сигнал

представляет собой гауссов пучок exp

- к

2^2)

^г и о ( х ) -f C . r ²⁾| g .^ у . [ x- X L | (15)

.=0               V' 0   < Рх 0 J где С. - коэффициенты разложения, у. (X) -сфероидальные функции.

Произвольная суперпозиция сфероидальных функций не будет обладать инвариантным характером.

Если мы имеем оптическую линзовую систему, осуществляющую двойное преобразование Фурье от исходного сигнала, можно получить следующее выражение:

Г г2 '

ГГ и 0 ( х ) « 1^0-и 0 - х^-Р х о    I ^Р у

Таким образом, после прохождения двух линз, как и следовало ожидать, оптический сигнал переворачивается и масштабируется.

В двумерном случае при квадратной апертуре двумерные сфероидальные функции

^ = 0.1. В этом случае количество сфероидальных функций, используемых для аппроксимации сигнала, равно 13. На рис. 2 показаны графики исходного сигнала (чёрный цвет) и его представления через сфероидальные функции (серый цвет). Погрешность аппроксимации составила 6%.

Сигнал, полученный после прохождения исходного гауссова пучка через линзовую систему в соответствии с (16), практически совпал с полученной аппроксимацией (среднеквадратичное отклонение составило 1%), т.е. искажение соответствовало погрешности аппроксимации.

Чтобы сигнал передавался без искажений, он должен быть согласован с суперпозицией набора сфероидальных функций, имеющих собственные значения, близкие к единице. Прохождение такой аппроксимации сигнала (см. рис. 2) произошло практически без искажений (среднеквадратичное отклонение составило 1,6%).

Таким образом, искажение сигнала можно оценивать без моделирования его прохождения

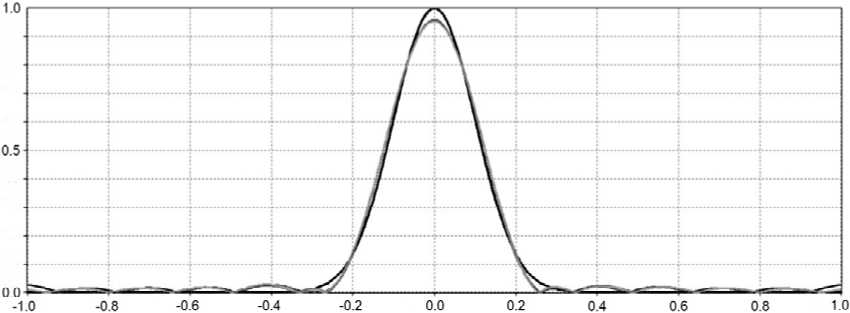
Рис. 2. Графики сигнала (черный цвет) и его аппроксимации (серый цвет)

через оптическую систему, а лишь на основе разложения по сфероидальным функциям, согласованным с параметрами этой системы.

• 4.    ЗАКЛЮЧЕНИЕ

В работе выполнен расчет собственных функций оператора прохождения оптического сигнала через систему из двух линз в соответствии с параметрами это системы. Произведено разложение одномерного гауссова сигнала по рассчитанным сфероидальным функциям. Показано, что аппроксимация сигнала набором сфероидальных функций, имеющих собственные значения, близкие к единице, передается практически без искажений (среднеквадратичное отклонение составило 1,6%). Причем оценивать искажение исходного сигнала при его прохождения через оптическую систему можно без моделирования, а лишь на основе погрешности аппроксимации, т.е. разложения по сфероидальным функциям.