Формирование оптического вихря сразу за сферической линзой при освещении ее светом с круговой поляризацией

Давно известны в оптике такие особенности острой фокусировки лазерного света, как формирование фокусного пятна эллиптической формы [1 – 4], если у света была линейная поляризация, или формирование в плоскости фокуса вращающегося потока энергии, если свет имел круговую поляризацию [5 – 8]. Последний эффект носит название спин-орбитальной конверсии [8]. Известно также, что с помощью неоднородной линейной поляризации (радиальной или азимутальной) можно сформировать круглое фокусное пятно с минимальным размером [9, 10]. Мы покажем, что хотя у света с круговой поляризацией и с радиальной поляризацией при фокусировке формируется круглое фокусное пятно, но форма фокусных пятен интенсивности отдельных поперечных декартовых компонент – эллиптическая. Также мы покажем, что эллиптическая форма фокусного пятна при фокусировке света с линейной поляризацией объясняется наличием оптического вихря второго порядка в каждой поперечной компоненте вектора напряженности электрического поля.

В [11] авторы впервые на основе теории Ричардса– Вольфа [2] показали, что при фокусировке света с круговой поляризацией у поперечных проекций вектора напряженности электрического поля в фокусе формируется оптический вихрь с топологическим зарядом +2 (правая круговая поляризация) или –2 (левая круговая поляризация). В [11] объяснили появление оптических вихрей в фокусе геометрической фазой Берри [12] и спиновым эффектом Холла [13]. Но детальной связи оптического вихря с геометрической фазой и оптическим эффектом Холла в [11] не показано. На основе работ [2, 14] мы покажем, что оптический вихрь формируется сразу после прохождения светом с любым состоянием поляризации через сферическую линзу. Будет видно, что в зависимости от азимутального угла φ декартовы компоненты начального поперечного светового поля будут четыре раза менять знак при одном обороте самого угла φ, то есть будут зависеть от sin(2φ) и cos (2φ).

В [15 – 17] рассматривался азимутальный поток энергии в фокусе когерентного света. Например, в [17] показано, что при фокусировке света с круговой поляризацией в остром фокусе формируется азимутальный (угловой) поток энергии в плоскости фокуса. В данной работе этот поток объясняется появлением поперечных и продольных оптических вихрей сразу после прохождения светом с круговой поляризацией сферической линзы.

В данной работе мы покажем, что:

• 1)    оптический вихрь второго порядка формируется в каждой поперечной декартовой компоненте сразу после прохождения света с круговой поляризацией через сферическую линзу;

• 2)    наличие этого оптического вихря сразу за сферической линзой объясняет, почему сразу за сферической линзой у света появляется орбитальный угловой момент;

• 3)    также этот оптический вихрь второго порядка объясняет эллиптическую форму интенсивности у декартовых компонент в плоскости фокуса;

• 4)    для света с линейной поляризацией после сферической линзы формируются два поперечных оптических вихря с топологическими зарядами +2 и –2;

• 5)    их наличием объясняется эллиптическая форма фокусного пятна для света с линейной поляризацией;

• 6)    обнаружить оптический вихрь у света с правой круговой поляризацией можно по наличию интенсивности на оптической оси в фокусе, при освещении сферической линзы оптическим вихрем с топологическим зарядом –2.

В (1) θ – это угол между оптической осью и отрезком, соединяющим точку геометрического фокуса с точкой на сходящемся сферическом фронте сразу за линзой (рис. 1). При этом точка на сферическом фронте, отстоящая от оптической оси на расстояние r , связана с фокусным расстоянием f соотношением: r = f sin θ, φ – азимутальный угол.

Далее мы найдем некоторые характеристики этого светового поля, если начальное поле описывается следующими векторами Джонса:

Е о ( ф )

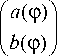
1 Г 1

22 ^ о i

Н о ( ф )

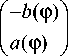
1 f-° i^

.

V211 )

То есть свет, освещающий сферическую линзу, имеет правую (σ = 1) или левую (σ = –1) круговые поляризации. Если начальное поле (2) подставить в (1), то получим следующие проекции векторов напряженности:

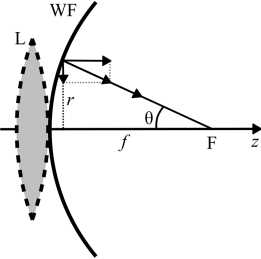
Рис. 1. Фокусировка света идеальной сферической линзой: L – линза, WF – сферический волновой фронт, F – геометрический фокус

E x = ' [ ( 1 + cos 0 ) - ( 1 - cos 0 ) e² ° ^{i ф} ] , 22

Ey = 1°_ [(1 + cos 0) + (1 - cos 0) e2°iф ],

E z = —^=sin 0 e ° ^{i ф} , 2

H_x - —~i= [( 1 + cos x     2^2 ^L(

H y ^- 212 ^{[( 1 +} cos ⁰

H z - -ⁱ ° sin 0 e ° ^{i ф} .

0 ) - ( 1 - cos 0 ) e² ° ^{i ф} ] ,

-

cos 0 ) e ² ° ^{i ф} J ,

Из (3) видно, что сразу за сферической линзой сформируется суперпозиция пучка с правой круговой поляризацией (σ = 1) и оптического вихря c топологическим зарядом 2σ и с левой круговой поляризацией:

E x | 1 + cos 0 f 1 ] 1 - cos 0 , f 1 —                            e 2°^ф

E y )     2^2 ^ ° i J    2^2       [ -о i

A ( 0 )sin(2 ф )

E x = (1 + A ( 0 ) cos ² ф ) a ( ф ) +----- 2—— b ( ф ),

A sin(2 ф )

E y —---2—- a ( ф ) + (1 + A ( 0 ) sin² ф ) b ( ф ),

E z =- sin 0 ( a ( ф )cos ф + b ( ф )sin ф ) ,

A ( 0 ) sin(2 ф )

H x =- (1 + A ( 0 )cos ² ф ) b ( ф ) + -^-2      a ( ф ),  (1)

Н у = - A sin(2 ^ ) b ( ф ) + (i + a ( 0 )sin 2 ф ) a ( ф ),

H z =- sin 0 ( - b ( ф )cos ф+ a ( ф )sin ф ) , A ( 0 ) = cos 0- 1.

Также оптический вихрь с топологическим зарядом σ сформируется у компоненты поля с продольной поляризацией E z . Причем оба вихря (поперечный и продольный) будут наиболее проявляться при больших углах наклона лучей, сходящихся в фокус, то есть при углах θ, близких к π/2. То есть оптический вихрь в основном будет на кольце, а в центральном круге сходящегося в фокус пучка оптического вихря не будет. Этот оптический вихрь, в свою очередь, создаст орбитальный угловой момент (ОУМ) у пучка сразу за сферической линзой, хотя до линзы у пучка не было ОУМ. Действительно, продольная компонента вектора ОУМ с учетом выражений (3) будет иметь вид [18]:

г т 1л ’ ЭEx. ЭEy      3Ez

L_z = Im I E x --+ E y —— + E z

Эф Эф     Эф

J a. В - f -^ f ] I" sin “⁺¹ [-'icos ³ “ [ cos ¹/² ( 0 ) X

I x J Jo       12)       12J (10)

= ° (1 - cos 0 ).

X B ( 0 ) e‘ k cos⁰ J p ( £ ) d 0 ,

А продольная компонента вектора спинового углового момента (СУМ) сразу за сферической линзой будет иметь вид:

S_z = 2 Im ( E X* E y ) = О cos 0 .

Из (6) видно, что, наоборот, продольная компонента спина максимальна вблизи оптической оси и спадает до нуля при увеличении угла θ до π/2. Из (5) и (6) можно найти полные СУМ и ОУМ сразу за сферической линзой:

L z = 2 л f ² J L_z sin 0 d 0 = 2W sin ⁴ ( 0 o / 2),

⁰                                                (7)

e2

Sz = 2 л f ² I Sz sin 0 d 0 = —sin ² (0_o), W = 2 л f 2 .

В (7) W – это мощность пучка света, прошедшего через линзу (интенсивность начального пучка считается единицей), f – фокусное расстояние сферической линзы. Из (7) видно, что максимальный ОУМ получается при числовой апертуре NA = sin θ 0 = 1 и равен половине мощности пучка, L_{z >max} = — / 2 . При этом продольная СУМ уменьшится на такую же величину, S z ,min - — - — / 2 - — / 2. Но это уменьшение СУМ не идет на увеличение ОУМ, а переходит в поперечный СУМ. Аналогично можно получить продольную проекцию вектора Пойнтинга сразу после сферической линзы:

P_z - Re ( E X H y - E y H_x ) - cos 0 .                  (8)

Сравнивая (6) и (8), можно видеть, что продольные проекции вектора спина и потока энергии совпадают с точностью до знака. Продольная проекция СУМ для левой круговой поляризации направлена против оптической оси z , а продольная проекция вектора Пойн-тинга всегда направлена вдоль положительного направления z .

• 2.    Свет с правой круговой поляризацией в плоскости фокуса

Световое поле (2) в плоскости фокуса будет иметь вид [2]:

^{E x} У/2⁽ J ^{0,0 +} e ■ J ²’'. ) .

^{Ey =} 72 ( J o’ - eJ '"° ) ’                      (9)

E z - - V е °^ф j i,° .

В (9) обозначены следующие функции от радиальной переменной r :

где k = 2π/λ – волновое число света с длиной волны λ, f – фокусное расстояние апланатической системы, ( r , φ, z ) – цилиндрические координаты, θ 0 – максимальный угол наклона лучей к оптической оси, определяющий числовую апертуру апланатической оптической системы NA = sin(θ 0 ), ξ = kr sin(θ). Из (9) получим выражения для интенсивностей по декартовым осям:

I x ^- E x ⁽ r , ф )|^{2 -}

- 2 ( J 0²,0 + J 2,2 + 2 J 0,0 J 2,2 cos(2 ф ) ) , Iу ^- | Ey ⁽ r , ф)Г ^-

^- 2 ( ^J 02,0 ^{+ J} 22,2 ^{- 2 J} 0,0 ^J 2,2 ^{cos(2 ф )} ) .

Причем выражения (11) будут одинаковыми и для левой, и для правой круговой поляризации. Из (11) видно, что интенсивности по декартовым осям имеют вид эллипса, который вытянут для I x вдоль оси x , а у интенсивности I y – вдоль оси y . Это эллиптическое распределение интенсивности можно измерить в эксперименте и тем самым убедиться, что в фокусе присутствует оптический вихрь с топологическим зарядом 2. Правда, как показано в [19], вклад в интенсивность вторых слагаемых в выражениях (9) много меньше, чем вклад первых слагаемых, поэтому этот эллипс будет слабо искаженным кругом.

Более эффективно использовать дополнительный вихрь, чтобы скомпенсировать оптический вихрь в (9) и получить слабую интенсивность в центре плоскости фокуса. Действительно, для начального поля вида pin ф

Е 0( ф ) - e 7=-

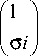
„ , . ein ^ф f -° i

^Н 0⁽ ф ) ^- , ,

в [17] получено выражение проекций электрического вектора в плоскости фокуса:

i n -i

E x ■ n - 72 e in ^ф ( J 0’ n + e ²° i^ J 2- n +2° ) ’

E y, _n - -i^e in ^ф ( J 0, n - e ²°^ф J 2,n +2° ) , y ’

E z , n --V i n e i^n ⁺°^)ф J 1, n +° .

Поэтому при n = –2σ в плоскости на оптической оси будет локальный максимум интенсивности, пропорциональный J ₂ ² _,0 . Этот максимум интенсивности доказывает наличие в фокусе поперечного оптического вихря с топологическим зарядом +2.

• 3.    Свет с линейной поляризацией в остром фокусе

Известно, что при фокусировке светового пучка с линейной поляризацией фокусное пятно приобретает эллиптическую форму. Как мы покажем, это объясняется тем, что после сферической линзы для линейной поляризации формируются два оптических вихря с топологическими зарядами 2 и – 2 с левой и правой поляризациями. Эти вихри вносят асимметрию в фокусное пятно. Действительно, вектор Джонса начального поля для оптического вихря с линейной поляризацией имеет вид:

E n ( ф ) = exp( in ф )

Проекции электрического вектора в плоскости острого фокуса для начального поля (14) имеют вид [20]:

n -1

E x = — e^{in ф} ( 2 J o, n + e^{2i ф} J 2n ₊ 2 + e-^{2i ф} J 2n - ₂ ) ,

E y = i ^ e in ^ф ( e ^-2 ‘^ф J 2, n -2 - e^{2i ф} J 2, n +2 ) ,                 (15)

E z = iⁿe^{in ф} ( e -‘^ф J 1, n -1 - e^ J 1, n + 1 ) .

В (15) максимальный вклад вблизи оптической оси дает слагаемое I 0, n . Остальные слагаемые в несколько раз меньше [19]. Из (15) видно, что в фокусе при n = 0 сформировались два оптических вихря с топологическими зарядами 2 и –2 у поперечных проекций поля и два оптических вихря с зарядами 1 и –1 у продольной компоненты поля.

C помощью (15) при n = 0 получим выражения для интенсивности отдельных компонент в фокусе для света с линейной поляризацией вдоль горизонтальной оси:

I x = E x ( r , ф)| ² =

= 2 ( 2 J 2,o + J 22,2 + 2 J 0,0 J 2,2 cos(2 ф ) ) ,

I y = E y ⁽ r , ф ) ² =

= 2 J 22,2 ( 1 ^{- cos(4} ф ⁾ ) ,

I Z = E z ⁽ r , ф)| ² =

= 2 J 121 ( 1 + cos( ф ) ) .

Из (16) видно, что все проекции интенсивности зависят от азимутального угла φ и не являются радиально симметричными. Но по величине основной вклад в интенсивность близи оптической оси, там, где расположено фокусное пятно, дает слагаемое J0,0, которое формирует круглое фокусное пятно. Вторым по величине слагаемым, дающим вклад в интенсивность, является слагаемое J0,0 J2,2 cos(2ф). Это слагаемое по форме является эллипсом, вытянутым вдоль горизонтальной оси, так как оно имеет два локальных максимума при φ = 0 и φ = π. По сумме этих двух слагаемых форма фокусного пятна для света с начальной линейной поляризацией будет иметь вид эллипса, вытянутого вдоль направления вектора поляризации. Таким образом, именно два оптических вихря с зарядами 2 и –2, которые сформировались при фокусировке, ответственны за эллиптическую форму фокусного пятна.

• 4.    Свет с радиальной поляризацией в остром фокусе

Вектор Джонса для светового поля с радиальной поляризацией имеет вид cos ф

Е ( ф ) = 1.2.                                   (17)

^ sin ф J

В плоскости фокуса проекции электрического вектора для начального поля (17) имеют вид [21]:

E x ( r , ф ) = cos( ф ) ( 1 0,1 - 1 2,1 ) ,

E y ( r , ф ) = sin( ф ) ( 1 0,1 - 1 2,1 ) ,                          (18)

Ez ( r , ф ) = 2 iI 1,0 .

Из (18) видно, что радиальная поляризация (17) сохраняется в фокусе, но модулируется функцией, зависящей от радиальной переменной ( 1 ₀,1 - 1 ₂,1 ) . Также видно, что интенсивность каждой поперечной координаты будет иметь форму эллипса, вытянутого вдоль соответствующей координатной оси, хотя полная поперечная интенсивность будет иметь круглую форму.

• 5.    Моделирование

Поперечные компоненты поля в фокусе (9) состоят из двух слагаемых, вторые из которых как раз описывают возникший оптический вихрь. Согласно [19], вклад вторых слагаемых в интенсивность много меньше, чем вклад первых слагаемых, если амплитуда начального поля постоянна или гауссова. Поэтому рассмотрим в этом параграфе ограничение поля кольцевой диафрагмой, блокирующей центральную часть пучка (рис. 2).

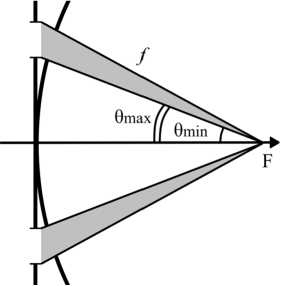
Рис. 2. Фокусировка света, ограниченного кольцевой диафрагмой с полярными углами θ min и θ max

Параметры моделирования: длина волны λ =532 нм, фокусное расстояние f = 20λ, диафрагма кольцевая, θmin = arcsin 0,95 ≤ θ ≤ arcsin 0,99 = θmax, амплитуда внутри кольца равномерная, т.е. A(θ) ≡ 1, поляризация правая и левая круговая, вектор Джонса [1, ±i]T, расчётная область |x|, |y| ≤ R =5 мкм.

На рис. 3 показаны распределения интенсивности в фокусе декартовых компонент (рис. 3 а , б ) и их суммы (рис. 3 в ).

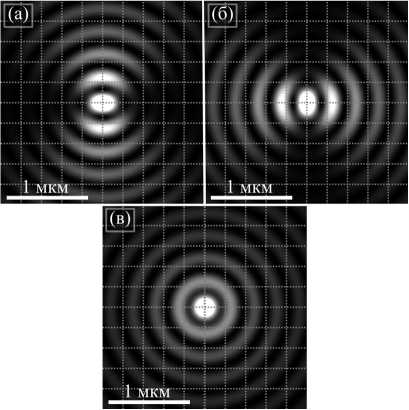
Рис. 3. Распределение интенсивности в фокусе для I x (а), I y (б) и I x + I y (в) для начального поля c круговой поляризацией (2)

Из рис. 3 видно, что фокусное пятно I x (без учета боковых лепестков) имеет вид эллипса, вытянутого вдоль горизонтальной оси, в соответствии с первой формулой в (11). Аналогично фокусное пятно I y (без учета боковых лепестков) имеет вид эллипса, вытянутого вдоль вертикальной оси, в соответствии со второй формулой в (11). При этом поперечное распределение интенсивности в фокусе (рис. 3 в ) имеет радиально симметричный вид.

На рис. 4 показаны поперечные распределения в фокусе для начального оптического вихря с топологическим зарядом n = 2 с левой (рис. 4 а ) и правой (рис. 4 б ) круговой поляризацией.

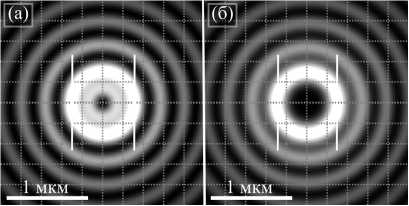
Рис. 4. Поперечные распределения интенсивности I x + I y в фокусе начального поля (12) при n = 3, и σ = –1, левой (а) и σ = 1, правой (б) круговой поляризации

Из рис. 4 видно, что на картине Ix + Iy основное кольцо (показано на рис. 4 вертикальными линиями) одинакового радиуса, но при левой круговой поляризации есть ещё кольцо внутри (тёмная область в центре мала) – это кольцо вихря с ТЗ n – 2 = 1. При правой круговой поляризации кольца внутри нет. Есть кольцо снаружи, это кольцо вихря с ТЗ n + 2 = 5, но оно не заметно из-за боковых лепестков вихря 3-го порядка.

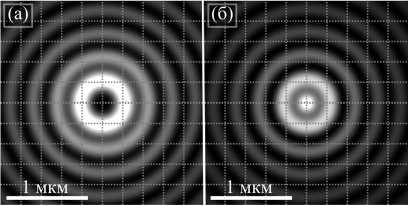
Рис. 5. Распределение интенсивности I x + I y в фокусе начального поля (12) при тех же параметрах, что и на рис. 4, но при n = –2 с σ = –1, левой (а), σ = 1, правой (б) круговой поляризацией

Из рис. 5 видно, что на картине поперечной интенсивности I x + I y при левой круговой поляризации формируется только кольцо, так как поле состоит из вихрей порядков –2 и –4. При правой круговой поляризации внутри кольца есть ещё пик интенсивности на оптической оси, так как поле состоит из двух слагаемых: вихревого I 0,2 e ^{–2 i φ} и радиально симметричного I 2,0 .

Рис. 3 – 5 доказывают, что при прохождении света с круговой поляризацией через сферическую линзу формируется оптический вихрь второго порядка ( n = 2σ). Хотя на распределении фазы в фокусе (рис. 6) этого вихря не видно. Виден только оптический вихрь первого порядка ( n = σ) в фазе продольной компоненты поля (9).

Рис. 6. Распределение фазы в плоскости фокуса начального поля (2): arg E x (а), arg E y (б) и arg E z (в). Черный цвет – фаза 0, белый цвет – 2π

На рис. 6 показаны фазы в фокусе для всех декартовых компонент электрического поля, полученные по формулам (9). Из рис. 6в хорошо видно, что у продольной компоненты вектора напряженности электрического поля в фокусе для света с правой круговой поляризацией формируется оптический вихрь с топологическим зарядом n = 1. А на рис. 6а, б трудно увидеть фазу оптического вихря с топологическим зарядом n = 2. Это объясняется малой величиной вторых слагаемых в первых двух уравнениях (9).

Заключение

В работе получены следующие результаты. Показано, что при фокусировке света с круговой поляризацией сразу за сферической линзой поперечное световое поле разделяется на два сходящихся в фокус световых поля, одно из которых по-прежнему является светом с той же круговой поляризацией, а второе (меньшее по величине) поле является оптическим вихрем второго порядка с круговой поляризацией противоположенного направления. Этот дополнительный оптический вихрь ответственен за появление орбитального углового момента светового поля сразу за сферической линзой. Но так как и оптический вихрь, и орбитальный угловой момент появляются не у всего поля, а только у некоторой части поля, то оба световых поля (и вихревое, и не вихревое) распространяются вместе, и по распределению полной интенсивности в фокусе их нельзя разделить. Оптический вихрь проявляется в эллиптической форме интенсивностей отдельных поперечных компонент поля в плоскости фокуса, а также он проявляется в появлении локального пика интенсивности на оптической оси, если в начальном поле присутствует оптический вихрь второго порядка с противоположенным знаком. В работе также показано, что при фокусировке света с линейной поляризацией у поперечных компонент светового поля формируются два оптических вихря второго порядка со знаками плюс и минус. Показано, что именно эти оптические вихри определяют эллиптическую форму фокусного пятна. Причем эллиптическое фокусное пятно определяется начальной поперечной проекцией и вытянуто вдоль той декартовой оси, по которой направлен вектор линейной поляризации.

Работа выполнена при поддержке гранта Российского научного фонда № 23-12-00236 (в части теории) и в рамках Государственного задания НИЦ «Курчатовский институт» (в части моделирования).