Формирование пленок в разряде в скрещенных полях

Тонкие пленки из различных материалов широко используются в технике [7]. В частности, представляют интерес пленки, создаваемые из графита. При некоторых условиях структура этих пленок имеет алмазоподобный характер [2], [5]. Одним из методов их получения является разряд в скрещенных полях. Этот тип разряда обладает высокой степенью ионизации газа и стабильностью, что обеспечивает достаточную скорость роста пленок и их однородность. В известных нам работах, связанных с получением тонких углеродных пленок, отсутствует четкое количественное сравнение результатов эксперимента и теории. Целью данной работы является создание простой модели образования пленок и сравнение расчетов, основанных на ней, с экспериментальными данными.

Для получения пленок использовался макет с системой коаксиальных электродов, представленный на рис. 1. Пленки формировались путем распыления внешнего электрода – катода. С целью исключения загрязнения пленок оба электрода были выполнены из графита. Подложкой служила стеклянная или кремниевая пластинка, установленная на шлифе. Такая конфигурация позволяла помещать в разрядный промежуток различные участки подложки. Пленки формировались в режиме постоянного тока. Макет устанавливался в соленоиде таким образом, чтобы разрядный промежуток находился в его центре, в области однородного магнитного поля, величина которого составляла 15 мТл.

В основу модели были положены следующие предположения:

• 1.    Атомы углерода появляются в разрядном промежутке вследствие эрозии катода под действием бомбардировки положительными ионами [1] и быстрыми атомами газа, образовавшимися в результате процесса перезарядки [6];

• 2.    Осаждение углерода на подложку происходит в результате диффузии атомов в газе; атомы углерода оседают на аноде и на подложке;

• 3.    Коэффициент прилипания атомов углерода к аноду и подложке равен единице;

• 4.    Имеет место неоднородный нагрев газа [4], [8].

Так как катод и анод обладают цилиндрической симметрией, уравнение диффузии и граничные условия записываем в цилиндрических координатах. На рис. 2 приведены система координат и обозначения основных параметров разрядного промежутка.

Коэффициент диффузии углеродных атомов зависит от температуры, поэтому для построения диффузионной модели необходимо учесть разогрев катода. Рассмотрим два случая. Первый случай: градиент температуры между анодом и катодом постоянен – T(r) . Второй случай: градиент температуры между катодом и анодом зависит от времени T(r, t) . Кроме того, во втором случае задача не будет стационарной, то есть интегральный поток атомов с поверхности катода по времени непостоянен

( ^{∂ с} ≠ 0).

∂ t

На рис. 3 приведено расчетное распределение толщины пленок по радиусу для 3 случаев. Зависимость температуры от времени в первом приближении выразим следующим образом:

T ( t ) = T a + (1 - e ^{- α t} ) ⋅ ( T k - T a ),

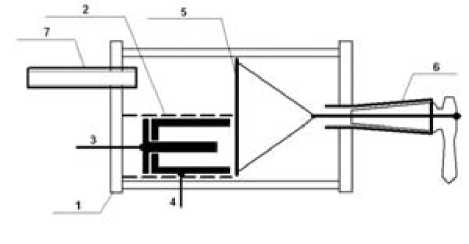
Рис. 1. Макет:

1 – стеклянный баллон, 2 – экран из стекла, 3 – анод, 4 – катод, 5 – подложка, 6 – шлиф для поворота подложки, 7 – откачка

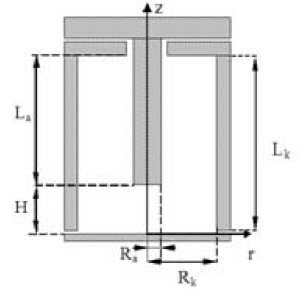
Рис. 2. Разрядный промежуток:

La, Ra – длина и радиус анода; Lk, Rk – длина и внутренний радиус катода; H – расстояние от торца анода до подложки. Lk= 54 мм, Rk= 9,5 мм, La= 45 мм, Ra = 2,5 мм, H = 10 мм

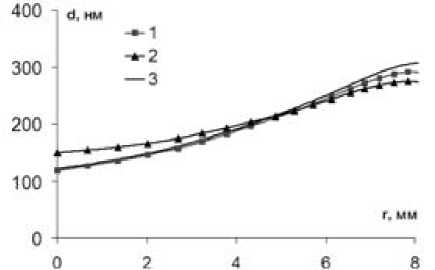
Рис. 3. Расчетное распределение толщины пленок по радиусу для пропущенного заряда q = 30 Кл, коэффициента распыления 0,5:

1 – интегральный поток атомов зависит от времени, температура изменяется по радиусу линейно, T(r) не зависит от времени; 2 – интегральный поток атомов зависит от времени, температура изменяется по радиусу линейно, T(r, t) зависит от времени; 3 – стационарная задача, интегральный поток атомов постоянен, температура T(r) по радиусу изменяется линейно

где T a – температура анода, Т к – температура катода, t – время, α – коэффициент насыщения температуры, который подбирался таким образом, чтобы к концу времени формирования пленок температура была максимальна.

На рис. 4 (а, б) приведена зависимость интегрального потока атомов углерода с поверхности катода от времени. Время установления потока в обоих случаях составляет порядка 10–3 с, рис. 4а. Из рис. 4б видно, что в случае, когда температура не зависит от времени, поток с течением времени остается постоянным, а когда температура изменяется со временем, поток атомов углерода с катода растет постепенно, но при этом изменяется в пределах малой величины, порядка

P = 6 - 10 14

ат .

с

Таким образом, учет зависимости градиента температуры по времени не вносит существенных изменений в расчеты толщины пленок, об этом свидетельствует рис. 3. Поэтому распределение температуры по радиусу T(r) будем считать линейным. При этом имеем стационарную задачу.

Уравнение диффузии, соответственно, имеет вид:

у ( D (T ( r )) I c ) + - D ( T ( r )) | c + D ( T ( r )) | 2 c = 0 , d r ^ d r ) r d r d z²

где c ( r , z ) и D ( T ) – концентрация и коэффициент диффузии атомов углерода в газе. Коэффициент диффузии бинарных смесей рассчитывался в соответствии с кинетической теорией [3]. Температуру газа непосредственно у поверхности анода считаем равной комнатной температуре. Температура у поверхности катода была измерена термопарой. Ее значение при условиях получения пленок составило 100 °C. Эта величина использовалась в расчетах. Учет зависимости температуры от z (по высоте катода) за счет нагрева торцевой части катода приводит лишь к несущественным изменениям (в пределах нескольких процентов). Поэтому температуру по высоте электродов считаем постоянной.

На оси цилиндра – условие симметрии:

| c (0, z ) = 0 , z e [0, H ] . d r

На распыляемой поверхности (катоде) задаем плотность потока:

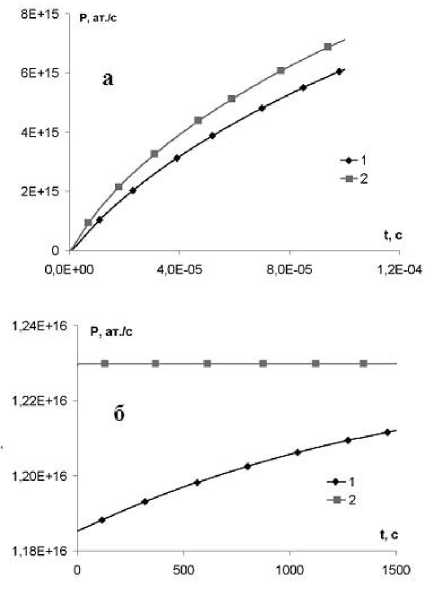
Рис. 4. Зависимость интегрального потока атомов углерода с поверхности катода от времени:

а – интервал установления потока 10^–4 с; б – время формирования пленки; 1 – температура изменяется по радиусу линейно, T(r, t) , зависит от времени; 2 – температура изменяется по радиусу линейно, T(r) , не зависит от времени

(1 +δ) ⋅γ⋅j D(T(r))∂c(r,Lk)=D(T(R))∂c=, ∂rk ∂re r∈ [Ra,Rk], z∈[0,Lk], здесь j – плотность разрядного тока, γ – коэффициент распыления (отношение числа выбиваемых атомов углерода к числу падающих ионов и атомов газа), δ – коэффициент перезарядки иона в собственном газе (отношение числа быстрых атомов газа, достигших катода после перезарядки, к числу ионов), e – заряд иона. Оценка показывает, что длина свободного пробега иона газа, соответствующая процессу перезарядки [1], в несколько раз меньше толщины катодного слоя; таким образом, большая часть ионов в пределах катодного слоя испытывает перезарядку. Поэтому коэффициент δ примем равным единице. При этом пренебрегаем эмиссией электронов под действием ионов, последние считаем атомарными и однозарядными. Для анода и подложки, где распыленное вещество оседает, примем условия:

c(Ra, z) = c(r,0) =0, z∈ [H,Lk], r∈ [0,Rk], то есть оседает все вещество. Решение этой краевой задачи позволяет определить поток на подложку, вычислить толщину пленки как функцию времени и распределение толщины пленки по радиусу.

Толщина пленки рассчитывалась в предположении плотной упаковки (простая кубическая кладка).

Для определения толщины пленки использовалась интерференционная картина, получаемая в отраженном свете при длине волны 546 нм. Она имела четкую круговую симметрию и содержала от 2 до 20 интерференционных колец в зависимости от пропущенного заряда. На рис. 5 приведена интерференционная картина для двух пленок, полученных при одинаковой величине прошедшего заряда и различных токах в неоне. Эксперимент показал, что основным фактором, определяющим распыление, является заряд, пропущенный через разрядный промежуток; при этом зависимость от тока незначительна (рис. 6).

На рис. 7 экспериментальные кривые распределения толщины пленки по радиусу, полученные при различных давлениях и одинаковом пропущенном заряде и токе в аргоне, сравниваются с расчетными, полученными при различных значениях коэффициента распыления γ. Кривая для большего давления соответствует меньшему эффективному коэффициенту распыления γ. Возможной причиной изменения эффективного γ является обратный возврат атомов углерода на поверхность катода. При большем давлении этот эффект должен проявляться сильнее.

На рис. 8 сопоставлен радиальный ход толщины пленки для двух газов. Опыт показывает, что при сравнимых давлениях и пропущенных зарядах эффективность распыления поверхности катода в неоне значительно больше.

Предложенная модель образования углеродных пленок с цилиндрической геометрией электродов охватывает основные аспекты процессов образования пленок и в достаточной мере согласуется с экспериментальными данными.

Рис. 5. Интерференционная картина пленок на кремниевой подложке: неон, λ = 546 нм, q = 30 Кл, ток 20 мA (слева), q = 30 Кл, ток 5 мA

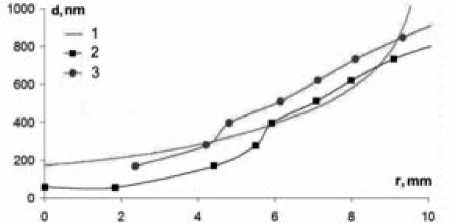
Рис. 6. Распределение толщины пленки по радиусу в неоне: 1 – модель, γ = 0,7, q = 30 Кл; 2 – I = 20 мА, q = 30 Кл, p = 0,2 Торр; 3 – I = 5 мА, q = 30 Кл, p = 0,2 Торр

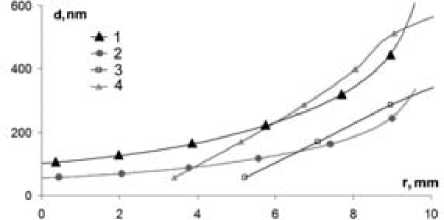
Рис. 7. Распределение толщины пленки по радиусу в аргоне при различных давлениях: 1 – модель, γ = 0,3, q = 48 Кл;

2 – модель, γ = 0,15, q = 48 Кл; 3 – I = 20 мА, q = 48 Кл, p = 0,16 Торр; 4 – I = 20 мА, q = 48 Кл, p = 0,04 Торр

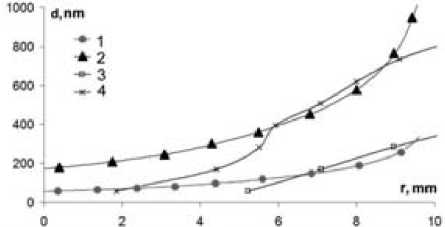
Рис. 8. Распределение толщины пленки по радиусу для двух газов (неон и аргон): 1 – модель, γ = 0,15, q = 48 Кл; 2 – модель, γ = 0,7, q = 30 Кл; 3 – аргон, I = 20 мА, q = 48 Кл, p = 0,16 Торр; 4 – неон, I = 20 мА, q = 30 Кл, p = 0,02 Торр