Формирование поляризационно-неоднородных лазерных пучков высокого порядка на основе пучков с круговой поляризацией

В последнее время всё большее внимание исследователей привлекают лазерные пучки с поляризационно-неоднородным распределением. Наибольший практический интерес представляют так называемые цилиндрические (с аксиальной симметрией) векторные пучки, которые имеют множество приложений, включая микроскопию, литографию, ускорение электронов, обработку материалов, высокоразрешающую метрологию, микроэллипсометрию и спектроскопию [1].

Известны различные схемы генерации аксиально-поляризованных пучков, использующие специальные устройства как внутри резонаторов, так и вне. Главным преимуществом внерезонаторных методов является универсальность. Внерезонаторные методы, как правило, основаны на когерентной суперпозиции пары обычных мод, например, с помощью интерферометра [2-4]. Таким способом можно формировать любые типы векторных пучков, и, в принципе, такой метод применим для любой длины волны.

Наиболее известный вариант интерференционного метода основан на сложении мод Эрмита-Гаусса (ЭГ) (0, 1) и (1, 0) с ортогональными линейными поляризациями. В этом варианте получается радиально-поляризованное распределение, соответствующее радиальной составляющей кольцевой моды Лагерра-Гаусса (ЛГ) (0, 1). Также может быть получена та же мода с азимутальным и смешанным типами поляризации в зависимости от знака и комплексного множителя при суммировании исходных мод. Исходные моды ЭГ получают разными способами. В работе [2] в качестве входного излучения использована одна мода, полученная внутрирезона-торным способом, из которой далее в специальной довольно сложной оптической схеме получена вторая мода, взаимно когерентная исходной, но с другой поляризацией. В работе [4] требуемая пара мод получается в специальном интерферометре из основной моды лазера, причём в каждом плече интерферометра установлены спиральные фазовые пла- стинки. Однако оптическая схема двойного интерферометра получается весьма сложной в сборке и юстировке, главной трудностью является реализация спиральной фазовой пластинки, работающей в нулевом порядке дифракции [5]. Из-за указанных трудностей экспериментальные результаты, представленные в работе [4], демонстрируют лишь удовлетворительное качественное совпадение с результатами численного моделирования.

Наконец, возможен вариант получения исходных мод при помощи дифракционных оптических элементов (ДОЭ). В работе [6] предложен специальный ДОЭ, выполненный на подложке из двулучепрелом-ляющего материала. Такой ДОЭ производит моду ГЭ (0, 1) в обыкновенном и ГЭ (1, 0) в необыкновенном лучах, которые формируются на определённом расстоянии. Далее моды подвергаются дополнительному фазовому преобразованию при помощи второго ДОЭ, после чего получается радиально-поляризованная мода ЛГ (0, 1). В качестве недостатков метода следует прежде всего отметить высокую сложность изготовления многоуровневого ДОЭ с максимальной высотой рельефа в несколько длин волн на кварцевой подложке. Видимо, по указанной причине в работе отсутствует натурный эксперимент с предложенными ДОЭ. Кроме того, такая пара ДОЭ предназначена лишь для формирования одной определённой моды с заданным типом поляризации и не допускает перестройки на другие типы поляризаций. Другой вариант использования ДОЭ был ранее предложен авторами данной статьи и состоит в использовании пары раздельных ДОЭ, производящих требуемые моды. Этот вариант был реализован авторами ранее в работах [7, 8] с использованием ДОЭ, формирующих лазерные пучки в нулевом порядке дифракции, а в работе [9] – с использованием бинарных ДОЭ с несущей частотой.

Кроме получения радиально-поляризованной моды ЛГ (0, 1), актуальной является задача получения радиально-поляризованных мод более высоких порядков, которые могут быть полезны в задаче ост- рой фокусировки и сверхразрешения. Однако получить ЛГ моды более высоких радиальных порядков, т.е. (n, 0), с помощью рассмотренного варианта интерференционного метода проблематично, так как в этом случае в суперпозиции участвует более двух мод ЭГ. В работе [4] был предложен и реализован метод преобразования цилиндрического пучка низкого порядка, полученного на выходе поляризационно-модового сумматора с помощью дополнительного аксикона, в моду Бесселя. Недостатком данного метода является, безусловно, наличие дополнительного оптического элемента. Кроме того, как было указано выше, сама схема получения цилиндрического пучка низкого порядка в работе [4] весьма сложна как в плане настройки, так и в плане изготовления элементов.

• 1.    Описание метода поляризационного суммирования на основе пучков с круговой поляризацией

• 2.    Экспериментальное формирование поляризационно-неоднородных пучков

Другой вариант получения радиально-поляризованных мод более высоких порядков [2] основан на суммировании двух пучков с круговой поляризацией. Один из пучков поляризован по правому кругу, а другой – по левому, причём пучки имеют фазовые сингулярности противоположных знаков. В зависимости от знака при суммировании пучков на выходе схемы получается либо радиальная, либо азимутальная поляризация. При этом никаких ограничений на радиальные распределения в суммируемых пучках не накладывается. Они лишь должны быть одинаковыми. Однако экспериментальная реализация указанного принципа в работе [2] натолкнулась на серьёзные трудности. Целью работы являлось преобразование гауссова пучка в пучок низкого порядка с радиальной поляризацией. Из-за несовершенства спиральных фазовых пластинок в работе [2] не удалось получить экспериментальных результатов приемлемого качества. Полученные распределения интенсивности как до анализатора, так и после него обладают сильной асимметрией, а интенсивность в центральной части пятна однородна и меняется в зависимости от положения анализатора. Всё указанное свидетельствует об отсутствии даже качественного совпадения экспериментальных результатов с результатами моделирования.

Трудности, связанные с изготовлением спиральных фазовых пластинок высокого качества, работающих в нулевом порядке дифракции, присутствуют и по сей день. Однако легко видеть, что реализация описанного принципа получения пучков с радиальной и азимутальной поляризацией очень хорошо укладывается в концепцию предложенной авторами схемы [9], где применяются ДОЭ с несущей частотой. Действительно, формирование пучков с вихревыми фазовыми сингулярностями в первом порядке дифракции хорошо известно [10, 11] и не вызывает никаких трудностей (в отличие от формирования их в нулевом порядке). Кроме того, образова- ние в плюс-минус первом порядках сопряжённых по фазе пучков полностью соответствует геометрии предложенной оптической схемы (рис. 1). Как легко видеть, складываться будут именно пучки с противоположными направлениями фазового винта, что и требуется в данном случае. Таким образом, ненужное или вредное в большинстве приложений свойство ДОЭ с несущей формировать сопряжённые порядки дифракции в данном случае является необходимым и полезным.

Применение ДОЭ даёт возможность решить одновременно и другую важную проблему, а именно: получение радиально-поляризованных мод более высоких порядков без дополнительных оптических элементов. Как отмечалось выше, никаких ограничений на радиальные распределения суммируемых пучков данный метод не накладывает. Это означает полную свободу в выборе формируемых данным методом цилиндрических векторных пучков, поскольку методы дифракционной оптики позволяют получать из основной моды лазера любые другие моды и пучки с высокой эффективностью.

Оптическая система для суммирования пучков с круговой поляризацией ничем не отличается от описанной ранее в [9], кроме наличия четвертьволновой пластинки перед каждым ДОЭ с несущей частотой вместо одной полуволновой пластинки перед первым ДОЭ. Также сформированные пучки дополнительно исследовались в фокусе Фурье-преобра-зующего объектива. Оптическая схема экспериментальной установки показана на рис. 1.

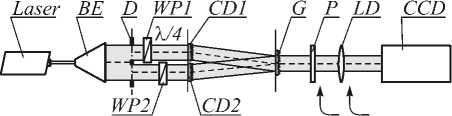
Рис. 1. Схема когерентного суммирования двух световых полей с круговыми поляризациями и фазовыми вихревыми пучками первого порядка с противоположными знаками.

BE – расширитель лазерного пучка, D – диафрагма, WP1, WP2 – четвертьволновые пластинки, CD1, CD2 – ДОЭ с несущей частотой,

G – дифракционная решётка, P – поляризатор-анализатор, L – Фурье-объектив, CCD – ПЗС-камера

Излучение лазерного источника оптического излучения с линейной поляризацией расширяется расширителем лазерного пучка ВЕ и освещает кодированные несущей частотой ДОЭ CD1 и CD2 через четвертьволновые пластинки WP1 и WP2, причём пластинки повёрнуты таким образом, чтобы один из ДОЭ освещался излучением, поляризованным по правому кругу, а другой – по левому. Каждый кодированный ДОЭ формирует пучки с фазовыми сингулярностями в +1-ом и –1-ом порядках дифракции, причём эти пучки являются комплексно-сопряжёнными. Пучки, сформированные в +1-ом порядке дифракции одного элемента и в -1-ом порядке дифракции другого элемента, распространяются в сходящихся направлениях и попадают на дифракционную решётку G, как показано на рис. 1. Решётка обеспечивает суммирование +1-го дифракционного порядка для одного ДОЭ и –1-го порядка для другого ДОЭ. Таким образом, обеспечивается суммирование комплексно сопряжённых пучков с противоположными направлениями фазовых вихрей, что и требуется для получения нужного результата. Изменение фазового сдвига между пучками в оптической системе осуществляется, как и ранее, за счёт сдвига дифракционной решётки поперёк оптической оси.

Для проведения экспериментов была реализована оптическая система в соответствии со схемой на рис. 1. На одну подложку были записаны три пары бинарно-амплитудных ДОЭ, формирующих фундаментальную гауссову моду, моду ЛГ (3, 0) и бессе-левый пучок (рис. 2) в ± 1-ом порядках. К каждому из пучков были добавлены вихревые фазовые составляющие первого порядка.

Бинарное кодирование элементов выполнялось с помощью метода частичного кодирования [12], позволяющего выдержать компромисс между точностью и дифракционной эффективностью формируемых пучков [13].

Запись амплитудных бинарных ДОЭ выполнялась при помощи кругового лазерного записывающего устройства CLVS-200. Каждый ДОЭ имел размер 2 x 2 мм с несущей частотой около 30 лин/мм, расстояние между парными ДОЭ составляло 10 мм. По той же технологии, но на другой подложке была изготовлена соответствующая дифракционная решётка.

В оптической схеме, представленной на рис. 1, в качестве лазерного источника использовался гелий-неоновый лазер ЛГН-215. Расширитель пучка включал 8× микрообъектив, диафрагму 50 мкм и коллимирующий объектив с фокусным расстоянием 300 мм. Параметры собранной оптической схемы были выбраны близкими к соответствующим параметрам оптической схемы, описанной в [7], для получения сравнимых результатов.

а)

Рис. 2. Вид бинарных кодированных ДОЭ, формирующих фундаментальную гауссову моду (а), моду ЛГ (3,0) (б) и бесселевый пучок с добавленными вихревыми фазовыми составляющими первого порядка (в)

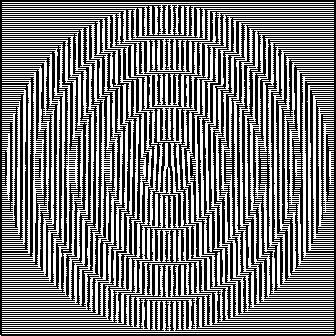
Сравнение с полученными ранее в [7] результатами показывает несколько более высокий уровень шумов на изображениях. Для борьбы с шумами, а также для проверки модовых свойств сформированных пучков были получены аналогичные распределения после прохождения Фурье-каскада, образованного объективом с фокусным расстоянием 750 мм. Такой выбор фокусного расстояния был обусловлен близостью размеров получаемых спектров к размерам исходных распределений.

На рис. 3 приведены распределения интенсивности, зафиксированные при отсутствии анализатора на выходе оптической схемы и в фокальной плоскости после введения дополнительной линзы.

Как видно из рис. 3, гауссовы пучки демонстрируют модовый характер – их распределение на выходе из конвертора и в дальней зоне (в фокусе линзы) практически не меняются. Бесселевый пучок также обладает присущими таким пучкам свойствами – при распространении в ближней зоне дифрак- ции имеется концентрация интенсивности в центральной части пучка, а в дальней зоне энергия переходит в периферийную зону. Явно выделяются два кольца, радиус которых связан с масштабом бесселевого пучка. Наличие двух спектральных колец вместо одного объясняется бинарной структурой оптического элемента, использованного для генерации бесселевого пучка [14].

На рис. 4 показано действие поляризационного анализатора при различных положениях на расстоянии 200 мм от решётки, а на рис. 5 – в фокальной плоскости линзы с фокусным расстоянием 750 мм. Структура распределений соответствует радиальной поляризации сформированных пучков, которая сохраняется при распространении пучков как в ближней, так и дальней зоне дифракции.

Возможность формирования широкого спектра радиально-поляризованных пучков полезна в задаче острой фокусировки и сверхразрешения [15].

В процессе юстировки данной оптической системы была также выявлена причина возможной асимметрии получаемых распределений интенсивности, которая кроется в кривизне волнового фронта пучка, освещающего ДОЭ. Только при точной юстировке коллиматора по картине интерференции пучков, отражённых от поверхностей наклонной плоскопараллельной пластины, расходимость освещающего пучка становится достаточно малой, чтобы были получены корректные результаты.

Заключение

Таким образом, предложен и экспериментально исследован новый подход к формированию пучков высшего порядка с радиальной поляризацией, основанный на сложении сформированных ДОЭ с несущей частотой пучков с противоположными направлениями круговых поляризаций и фазовых вихрей.

а)

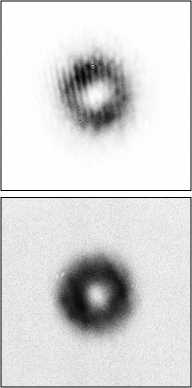
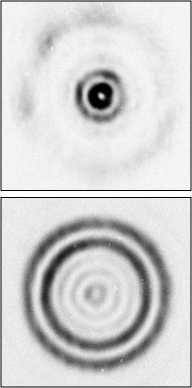
Рис. 3. Вид пучков низшего (а) и высшего порядка (б), (в) с радиальной поляризацией на расстоянии 200 мм от решётки (верхняя строка) и в фокальной плоскости линзы с фокусным расстоянием 750 мм (нижняя строка)

в)

а)

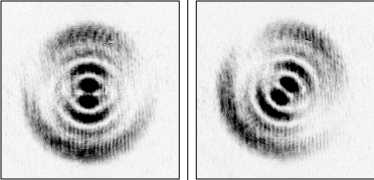
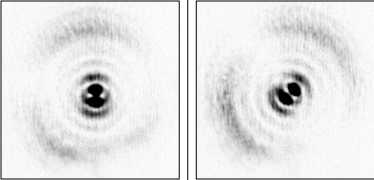
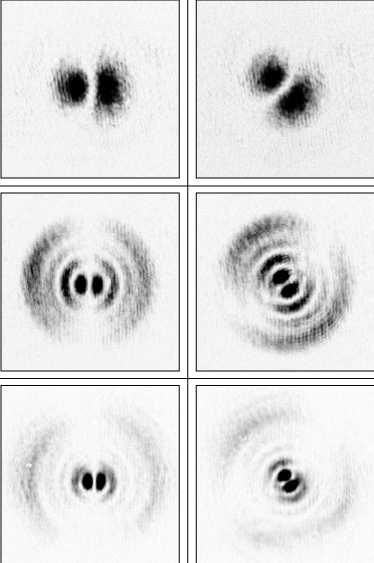
Рис. 4. Распределения интенсивности (негатив) на выходе оптической схемы при различных положениях анализатора (1 - вертикальное расположение, 2 - повёрнутое вправо на 45 ° 3 - горизонтальное положение, 4 - повёрнутое влево на 45 ° для радиально-поляризованного пучка низшей гауссовой моды (а), гауссовой моды высокого порядка (б), бесселевой моды (в), полученных суперпозицией пучков с круговой поляризацией

Рис. 5. Распределения интенсивности (негатив) в фокальной плоскости линзы, установленной на выходе оптической схемы при различных положениях анализатора для радиально-поляризованного пучка низшей гауссовой моды (а), гауссовой моды высокого порядка (б), бесселевой моды (в), полученных суперпозицией пучков с круговой поляризацией

Данный подход экспериментально реализован на основе доработки предложенной ранее системы когерентного сложения полей, включавшей ДОЭ с несущими частотами. Предложенная схема позволяет легко получать лазерные пучки с радиальной и азимутальной поляризацией и произвольным распределением радиальной амплитуды. Такие пучки могут быть полезны в задаче острой фокусировки и сверхразрешения.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов РФФИ 10-07-00109-а, 10-07-00438-а, 11-07-00153-а и гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.9.