Формирование признаков на основе методов вычислительной топологии
Автор: Чуканов Сергей Николаевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы и анализ данных
Статья в выпуске: 3 т.47, 2023 года.
Бесплатный доступ
Использование традиционных методов алгебраической топологии для получения информации о форме объекта связано с проблемой формирования малого количества информации: чисел Бетти и характеристик Эйлера. Центральным инструментом топологического анализа данных является метод персистентной гомологии, который суммирует геометрическую и топологическую информацию в данных с использованием персистентных диаграмм и баркодов. На основе методов персистентной гомологии может быть выполнен анализ топологических данных для получения информации о форме объекта. Построение персистентных баркодов и персистентных диаграмм в вычислительной топологии не позволяет построить гильбертово пространство со скалярным произведением. Возможность применения методов топологического анализа данных основана на отображении персистентных диаграмм в гильбертово пространство; одним из способов такого отображения является метод построения персистентного ландшафта. Его преимущества заключаются в том, что он обратим, поэтому он не теряет никакой информации и имеет свойства персистентности. В работе рассматриваются математические модели и функции представления объектов персистентного ландшафта на основе метода персистентной гомологии. Рассмотрены методы преобразования персистентных баркодов и персистентных диаграмм в функции персистентного ландшафта. С функциями персистентного ландшафта ассоциируется ядро персистентного ландшафта, которое формирует отображение в гильбертово пространство со скалярным произведением. Предложена формула для определения расстояния между персистентными ландшафтами, которая позволяет находить расстояния между изображениями объектов. Функции персистентного ландшафта отображают персистентные диаграммы в гильбертово пространство. Приведены примеры определения расстояния между изображениями на основании построения функций персистентного ландшафта этих изображений. Рассмотрены представления топологических характеристик в различных моделях вычислительной топологии. Расширены результаты для модулей персистентности с одним параметром на многопараметрические модули персистентности.
Распознавание образов, многопараметрический персистентный ландшафт, гильбертово пространство, топологический анализ данных
Короткий адрес: https://sciup.org/140300072
IDR: 140300072 | DOI: 10.18287/2412-6179-CO-1190
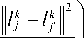
Список литературы Формирование признаков на основе методов вычислительной топологии
- Carlsson G. Topology and data. Bulletin of the American Mathematical Society 2009; 46(2): 255-308. DOI: 10.1090/S0273-0979-09-01249-X.
- Edelsbrunner H, Harer JL. Computational topology: an introduction. American Mathematical Society, 2010. ISBN: 978-0-8218-4925-5.
- Kusano G, Hiraoka Y, Fukumizu K. Persistence weighted Gaussian kernel for topological data analysis. Int Conf on Machine Learning (PMLR) 2016: 2004-2013.
- Hofer C, et al. Deep learning with topological signatures. NIPS'17: Proc 31st Int Conf on Neural Information Processing Systems 2017: 1633-1643.
- Hatcher A. Algebraic topology. Cambridge UP; 2005. ISBN: 978-0-521-79160-1.
- Zomorodian AJ. Topology for computing. Cambridge University Press; 2005. ISBN: 978-0-521-83666-1.
- Bubenik P. The persistence landscape and some of its properties. In Book: Topological data analysis. Cham: Springer; 2020: 97-117. DOI: 10.1007/978-3-030-43408-3_4.
- Pun CS, Xia K, Lee SX. Persistent-homology-based machine learning and its applications--A survey. arXiv preprint. 2018. Source: https://arxiv.org/abs/1811.00252. DOI: 10.48550/arXiv.1811.00252.
- Ghrist R. Barcodes: the persistent topology of data. Bulletin of the American Mathematical Society 2008; 45(1): 61-75. DOI: 10.1090/S0273-0979-07-01191-3.
- Mischaikow K, Nanda V. Morse theory for filtrations and efficient computation of persistent homology. Discrete & Computational Geometry 2013; 50(2): 330-353. DOI: 10.1007/s00454-013-9529-6.
- Xia K. A quantitative structure comparison with persistent similarity. arXiv preprint. 2017. Source: https://arxiv.org/abs/1707.03572. DOI: 10.48550/arXiv.1707.03572.
- Chukanov SN. Comparison of objects' images based on computational topology methods. Informatics and Automation 2019; 18(5): 1043-1065. DOI: 10.15622/sp.2019.18.5.1043-1065.
- Chukanov SN. The comparison of diffeomorphic images based on the construction of persistent homology. Automatic Control and Computer Sciences 2020; 54(7): 758-771. DOI: 10.3103/S0146411620070056.
- Vipond O. Multiparameter persistence landscapes. J Mach Learn Res 2020; 21(61): 1-38.
- Botnan MB, Lesnick M. An introduction to multiparameter persistence. arXiv preprint. 2022. Source: https://arxiv.org/abs/2203.14289. DOI: 10.48550/arXiv.2203.14289.
- Adcock A, Carlsson E, Carlsson G. The ring of algebraic functions on persistence bar codes. arXiv preprint. 2013. Source: https://arxiv.org/abs/1304.0530.
- Kwitt R, et al. Statistical topological data analysis-a kernel perspective. NIPS'15: Proc 28th Int Conf on Neural Information Processing Systems 2015; 2: 3070-3078.
- Sriperumbudur BK, Fukumizu K, Lanckriet GRG. Universality, characteristic kernels and RKHS embedding of measures. J Mach Learn Res 2011; 12(7): 2389-2410.
