Формирование пространства признаков для обнаружения живых объектов в здании на основе экологических факторов

Работа выполнена при государственной поддержке Министерства образования и науки РФ (грант № 074-U01).

ПОСТАНОВКА ЗАДАЧИ

Проблема обнаружения живых объектов в здании является актуальной для энергосбережения и обеспечения безопасности в помещениях. Как показывают результаты предыдущих исследований [1-7], более точное решение данной проблемы связано с анализом экологических факторов, что позволило повысить энергосбережение с 30% до 42% [1-3]. С другой стороны такие системы точного обнаружения позволяют определить поведение и перемещение живых объектов без использования камеры, что представляет значительный интерес из-за необходимости соблюдения конфиденциальности информации.

работе результаты показали наибольшую точность для метода LDA по сравнению с результатами аналогичных исследований.

В свою очередь, логистическая регрессия имеет ряд достоинств по сравнению с LDA [8-14], в частности, даёт лучшие результаты, поскольку основана на менее жёстких гипотезах. Кроме того, логистическая регрессия предпочтительнее, так как не вводит избыточную сущность как LDA, который сводит задачу классификации к более сложной задаче восстановления плотностей вероятностей [8].

Однако в работе[4]отмечается, что реализация модели логистической регрессии на используемом наборе данных невозможно, так как алгоритм расходится для линейно разделимых классов. Следовательно, было бы интересно оценить возможности логистической регрессии в контексте задачи, описанной в [4], более детально, проанализироватьуказанное ограничение и попытаться реализовать модель логистической регрессии при решении задачи обнаружения живых объектов в здании.

ОПИСАНИЕ НАБОРА ДАННЫХ

Исходные наборы данных для решения поставленной задачи доступны в UCI Machine Learning Repository по ссылке datasets/Occupancy+Detection+. Данные наборы могут быть использованы как для обучения, так и для тестирования моделей. Для сбора данных было использовано помещение 5,85 х 3,50 х 3,53 м, в котором были измерены следующие экологические факторы: уровни температуры, влажности, света и CO2, с помощью датчиков, установленных в помещении. Кроме того, для формирования меток – отсутствия или присутствия живого объекта в помещении – была установлена цифровая камера, которая снимала изображения с заданным интервалом времени. Таким образом, представленны-евыше признаки, дополнены отсчетами времени и влагоемкостью. Результирующий показатель в наборах соответствует статусу – обнаружен, не обнаружен – и определяет метки классов. Более подробное описание процедуры сбора данных представлено в работе [4].

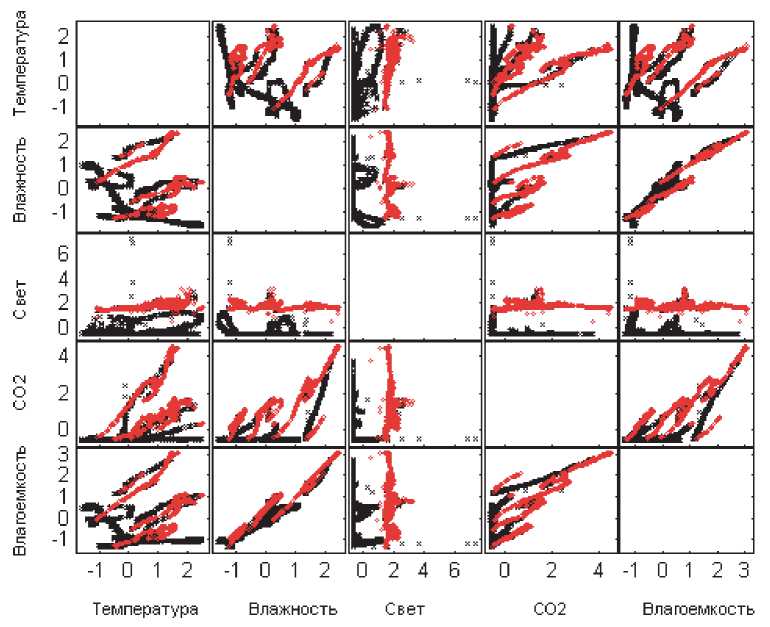
Обучающая выборка содержит 8143 реализации, которые были получены, когда дверь в помещение была закрыта. Два тестовых набора по 1998 реализаций каждая были сформированы для двух случаев: открытой и закрытой двери. На рисунке ниже представлены исходные наборы в зависимости от имеющихся признаков, исключая отсчеты времени. Метки классов размечены в виде черных крестиков в случае отсутствия объекта и красных точек в случае его присутствия в помещении (см. рис. 1).

Исходя из описания данных, представим задачу обнаружения объектов в здании как задачу бинарной классификации исходного набора данных с формированием пространства признаков. В качестве метода классификации определим нереализованный в проведенных ранее исследованиях [4] метод логистической регрессии и проанализируем его эффективность.

ФОРМИРОВАНИЕПРОСТРАНСТВА ПРИЗНАКОВ

Приведем основные понятия и определения, необходимые для решения поставленной задачи обнаружения объектов с помощью модели логистической регрессии.

Определение 1. Пусть X – множество объектов, Y – множество допустимых ответов. Объекты описываются числовыми признаками          ,

, где n – количество признаков. Тогда в русле работы [8] вектор               , где

, называется пространством признаков объекта x.

Определение 2. Пусть X – множество объектов, Y – множество допустимых ответов, а Θ – множество допустимых значений пространства параметров θ . Тогда в русле работы [10] параметрическим семейство                     , где

– фиксированная функция, называется моделью алгоритмов.

Задача 1. Пусть в качестве модели алгоритмов выбрана модель логистической регрессии 1

⁹^^Х’^ - 1 + exp (-9^тх)"

Тогда задача определения пространства параметров по выборке прецедентов , где           , сводится к минимизации логарифмической функции потерь [8]

i lnL(0,Xz) =

^ln(l + ехр(-О^тХ1уОУ

i=l

При этом в постановке Задачи 1 значение y_i=0 соответствует случаю отсутствия объекта, а y_i=1 – случаю присутствия объекта.

а)

б)

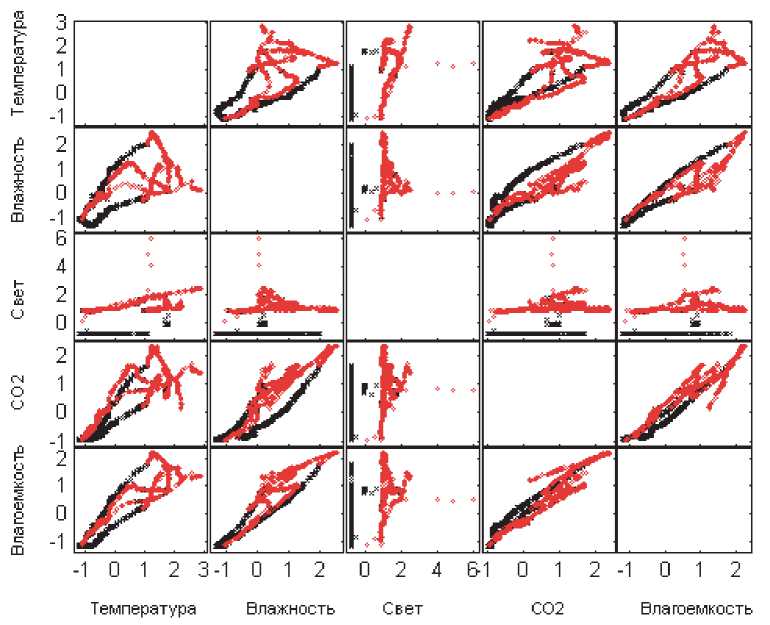
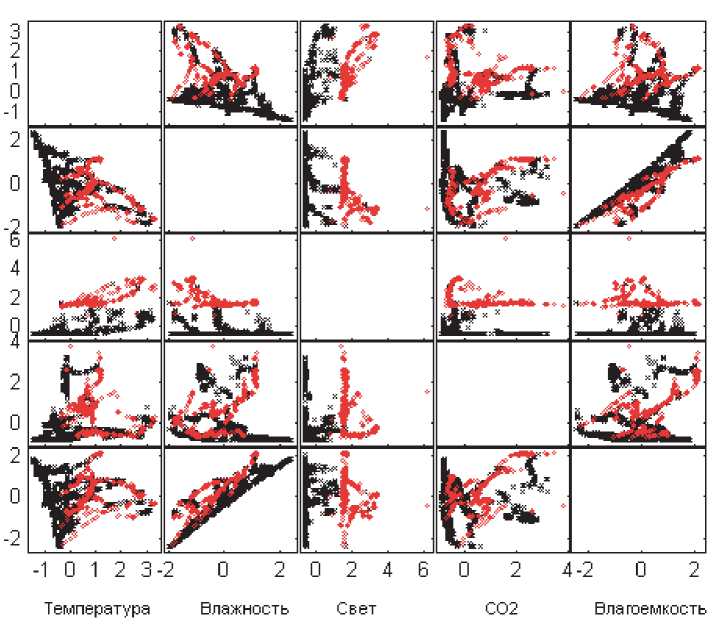
Рис. 1. Исходные данные:

а - обучающая выборка; б - тестовая выборка (закрытая дверь); в - тестовая выборка (открытая дверь)

Сформируем пространство признаков с учетом взаимной корреляции признаков. С этой целью построим таблицу корреляций признаков для обучающей выборки X l=(x.,у)=1 и тестовых выборок X ki=(x ,yi)ki=1 и X k2=(xt ,yi)k2=1. Согласно структуре исходных данных 1=6107, k1=1998, k2=1998; n=5, xj = {Температура, Влажность, Свет, СО2, Влагоём-кость}. Заметим, что часть данных из обучающей выборки было использовано для проведения кросс-валидации.

Зададим функционал для формирования пространства признаков x j = f(x) для пары { x p , x q }, где

Таблица 1. Коэффициенты корреляции между признаками x^j для выборок X ^l , X ^k 1 и X ^k 2

	xj с X1					xj с Xkl					xj с Xk2
j	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
1	1,00	-	-	-	-	1,00	-	-	-	-	1,00	-	-	-	-
2	-0,15	1,00	-	-	-	0,71	1,00	-	-	-	-0,48	1,00	-	-	-
3	0,65	0,04	1,00	-	-	0,77	0,56	1,00	-	-	0,70	-0,2	1,00	-	-
4	0,56	0,44	0,66	1,00	-	0,87	0,91	0,77	1,00	-	0,22	-0,1	0,23	1,00	-
5	0,15	0,96	0,23	0,63	1,00	0,89	0,95	0,70	0,96	1,00	-0,03	0,88	0,15	0,05	1,00

, , в следующем виде d m f^.x^d) = П Пор)™-71^9)11, m=l n=0

где              . При этом в данном исследо вании выбиралась пара {p,q} , соответствующая признакам с наибольшей корреляцией на обучающей выборке        (см. табл. 1).Исключени- ем являлась пара {2,5}, которая линейно зависима по определению [4].

Рассмотрим различные комбинации признаков          в виде наборов:

• 1.;

• 2.;

• 4.;

• 5.;

• 6.

РЕЗУЛЬТАТЫ РАСПОЗНАВАНИЯ

Проанализируем приведенные выше комбинации и исследуем возможность минимизации набора признаков. В таблице 2 приведены значения точности распознавания для наборов { Gr } ⁶ _r=1 при различных значениях величины d = {2,4,6} на обучающей выборке и двух тестовых выборках. Следует отметить, что при формировании наборов была проведена нормировка значений для повышения качества и скорости сходимости выбранной модели классификации [8]. Нормировка пространства признаков также необходима из-за выбора степенного функционала f ( x^p, x^q, d ) – возведение в степень слишком больших или слишком маленьких значений может привести к неадекватным результатам. Модель логистической регрессии была реализована в системе GNU Octave 3.8.2

и апробирована при проведении экспериментальных исследований на MacBookAir 11 OS X EI Captain с процессором 1.3 GHzIntelCore i5 и памятью 4 GB 1600 MHz DDR3.

Как видно из таблицы, повышение сложности пространства признаков не приводит к существенному повышению качества распознавания: точность классификации как среднее лучших показателей (выделено жирным) при d = 2 на 0,85% хуже, чем при d = 4, и на 0,25% хуже, чем при d = 6. Более того, обращает на себя внимание тот факт, что при d = {2,4} наилучшая точность получена для результатов, где при формировании признаков использовался функционал f ( x¹,x³,d ) с парой признаков {1,3} .

Согласно результатам исследований, приведенных в [4], хорошее качество классификации-было получены приполном наборе G₀ : x^j – 97,90% для тестового набора X^k 1 и 98,76% для тестового набора X^k 2 .Данные результаты были получены с помощью LDA.Тем не менее, отмечается, что наилучший результат для набора X^k 1 – 97,9% был также получен на паре признаков {1,3}, а для набора X^k 2 – 99,33% на полном наборе, но дополненном парой вновь сформированных признаков, учитывающих временную компоненту. Представленные результаты были тоже получены с использованием LDA.

Анализируя таблицу 1, можно заметить, что пара признаков {1,3} является единственной, которая имеет высокую корреляцию как всех выборках: X ^l , X ^k 1 и X ^k 2 . Следовательно, использование корреляции при формировании пространства признаков является целесообразным. Проведем серию дополнительных вычислительных экспериментов при d = 1, включив в рассмотрение полный набор признаков x^j без дополнительного преобразования. Кроме того, для сравнения

Таблица 2. Точность распознавания при формировании наборов { Gr } ⁶ _r=1 при d = {2,4,6}

	d = 2			d = 4			d = 6
	X1	Xk i	Xk 2	X1	Xk i	Xk 2	X1	Xk i	Xk 2
G	98,4608	92,8929	85,8359	99,1158	94,5445	89,0891	98,9520	90,8408	90,9910
G	98,4117	91,1411	89,0891	98,8701	94,4444	82,8829	98,6900	91,8919	97,9980
g 4	98,7392	93,2933	93,8438	99,1158	93,1932	91,0410	99,1813	89,8899	92,5926
G3	93,6794	73,7738	69,8699	95,2186	74,0240	54,8549	94,9894	75,7758	65,5656
G2	98,5754	91,7918	96,1962	98,8374	94,4444	92,2422	98,6573	92,9429	94,9450
G	98,6573	75,5756	97,1471	99,0175	76,4764	97,5976	98,9029	76,3763	94,8949

Таблица 3. Точность распознавания при формировании наборов { G_r }⁶_r=0 при d = 1

С нормировкой Без нормировки X1 Xk Xk X1 Xk Xk2 G6 98,4444 87,9379 94,3443 98,4444 97,3974 96,9469 G5 98,6737 89,5896 97,0971 98,6900 97,8478 99,1992 G. 98,6737 88,738739 97,1972 98,6737 97,9980 99,2492 Gs 92,6314 79,2793 70,7207 91,0431 86,9369 77,2773 G2 98,6900 89,7397 97,1471 98,7064 97,8979 99,1992 G^ 98,8701 79,3293 99,3493 98,8538 97,9980 99,3494 Go 94,0888 96,9970 85,8358 98,6737 97,8979 99,1992 результатов с результатами, представленными в [4], проанализируем качество классификации как с нормировкой, так и без нормировки пространства признаков (см. табл. 3).

Из представленной таблицы следует, что точность распознавания без нормировки пространства признаков значительно выше. Результаты, полученные в данном исследовании с помощью логистической регрессии – 98% для набора X^k 1 и 99,35% для набора X^k 2 ,– аналогичны представленным в [4] для LDA, но реализуют более простую и легко интерпретируемую модель.

ВЫВОДЫ

В данной работе:

• 1.    реализована модель логистической регрессии, являющаяся более простой и интерпретируемой по сравнению с рассмотренными ранее;

• 2.    предложен метод обучения классификатора на основе формирования признаков с учетом взаимной корреляции и выявлена пара наиболее информативных признаков.

Автор выражает благодарность д.т.н., профессору С.А. Прохорову и к.ф.-м.н., профессору Л.П. Усольцеву за ценные замечания и рекомендации, способствующие повышению качества представления результатов исследований.