Формирование пространственно-неоднородных оптических структур вследствие параметрической модуляции в широкоапертурных лазерах

Интерес к области исследования формирования оптических структур в широкоапертурных оптических системах обусловлен техническим прогрессом оптических информационных технологий. Активным элементом в них являются миниатюрные источники высококогерентного излучения, такие как полупроводниковые лазеры с вертикальным резонатором и твердотельные лазеры на микрочипах. Подобные лазеры обладают высокими коэффициентами усиления и могут обладать короткими продольными размерами активной среды. Усиление мощности в них осуществляется в том числе и за счёт увеличения ширины апертуры, т.е. числа Френеля. Таким образом, указанные источники излучения могут быть широкоапертурными. Однако именно в лазерах с большими числами Френеля теоретически предсказывается и наблюдается экспериментально сложное распределение оптического поля, пространственновременная динамика которого до сих пор изучена недостаточно.

Поскольку в оптических информационных системах источники излучения могут использоваться в режиме прямой токовой модуляции (параметр накачки), важно обладать средствами прогнозирования и управления поперечной структурой оптического поля в зависимости от различных параметров эксплуатации источников. Известно, что периодическая модуляция параметров в однородной распределенной системе может приводить к параметрической неустойчивости Фарадея и возникновению так называемой ряби Фарадея (пространственно-неоднородных структур) [1 – 3]. C точки зрения практического применения интересно исследовать влияние периодической модуляции накачки на формирование пространственновременных оптических структур в широкоапертурных лазерах, что и было осуществлено в настоящей работе.

Математическая модель

Система уравнений Максвелла–Блоха, моделирующая пространственно-временную эволюцию оптического излучения в плоско-параллельном резонаторе, заполненном усиливающей двухуровневой средой, имеет вид:

дE /д t = g( P - E) + ia А± E,дP/д t = -(1 + i 5) P + DE,дD/дt = -y [D - r + 0,5 (E*P + EP*)],

где E,P,D – безразмерные огибающие электрического поля, поляризации и инверсии населённости соответственно; о = к / у_ъ у = уц/ у_± ; к , уц, у_± - скорость затухания поля в резонаторе, скорости релаксации инверсии и поляризации соответственно; 5 = ( w a - w c )/ у ± - отстройка между центром линии усиления и частотой резонатора, нормированная на полуширину линии усиления; А_± - двумерный лапласиан, x , у - безразмерные поперечные координаты; a – дифракционный параметр; r – накачка, нормированная на пороговое значение.

При 5 <0 система (1) имеет стационарное решение системы в виде пространственно-однородного решения, соответствующего приосевой генерации поля (с поперечным волновым числом k =0):

Dst (к = 0) = 1 + (5/(а +1))2, |Est (к = 0)|2 = r — 1 -(5/(о +1))2,

Pst (к = 0) = E„ (к = 0).(1 - i5/(g + 1)),Q( к = 0 ) = -5а/(а +1).

Наиболее важно исследовать возникновение неустойчивости Фарадея в широкоапертурных лазерах динамического класса B (у << □ << 1), поскольку именно к данному динамическому классу относятся полупроводниковые и твердотельные лазеры, используемые в оптических каналах связи. Известно, что для узкоапертурных лазеров (работающих на фундаментальной поперечной моде) временная модуляция параметра накачки приводит к временной модуляции выходной интенсивности. Известно, что амплитуда колебаний выходной интенсивности зависит от частоты модуляции накачки. Данная зависимость имеет вид резонансной кривой. Максимальная амплитуда временной модуляции интенсивности наблюдается при частоте модуляции накачки, равной частоте релаксационных колебаний:

® rei = V 2oy| E_S1 2 d Ds, .                                (3)

Параметр накачки модулировался во времени по гармоническому закону:

r (t) = r0 (1 + m ■ sin (Qt)).                              (4)

Здесь m , Q - параметры модуляции: глубина и частота соответственно.

Результаты численного моделирования

Численное моделирование системы (1) проводилось с помощью псевдоспектрального Фурье-метода экспоненциального дифференцирования типа Рунге– Кутта (ETD3RK) третьего порядка точности по временному шагу с периодическими граничными условиями [4].

В настоящей работе исследовалось формирование структур в зависимости от параметров модуляции накачки, остальные параметры были фиксированы и соответствуют динамическому лазеру класса В: □ = 0,1, Y = 0,001, a = 0,0001. Была построена диаграмма устойчивости однородного решения при данных параметрах в зависимости от двух параметров накачки r и отстройки 5 (представлена на рис. 1).

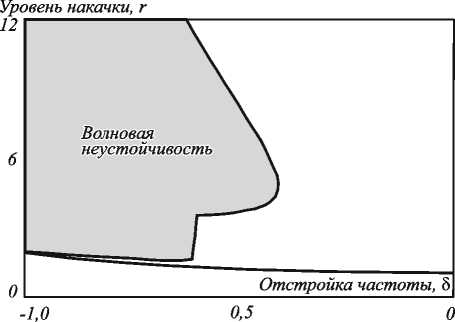
Рис. 1. Увеличенный фрагмент бифуркационной диаграммы при параметрах σ = 0,1; γ = 0,001

Значения параметров накачки r и отстройки 5 подбирались такими, чтобы оптическая система не попадала в область волновой неустойчивости [5–7]. Используя такие значения параметров, можно исключить спонтанное возникновение пространственно-временных оптических структур и изучать возникновение структур исключительно в результате развития параметрической неустойчивости. Пространственно-одно- родное решение зависит от параметра накачки r. Поэтому колебания во времени параметра (4) приводят также к колебаниям пространственно-однородного профиля (2) во времени. Стандартный линейный анализ устойчивости в данном случае оказывается неприменим для анализа механизмов формирования пространственных структур. Поэтому для исследования устойчивости колеблющегося пространственного однородного профиля интенсивности был адаптирован обобщённый метод Флоке, позволяющий исследовать устойчивость колебаний пространственно-однородного профиля по отношению к малым пространственно-временным возмущениям [8].

На рис. 2 приведены диаграммы устойчивости пространственно-однородных колебаний в плоскости параметров ( m , Q ) для параметров □ = 0,1, у =0,001, a = 0,0001, r 0 = 5 при различных отстройках. Серым цветом выделена область параметрической неустойчивости, в которой по крайней мере один показатель Флоке положительный. Это означает, что в данной области прогнозируется формирование пространственных структур вследствие временной модуляции накачки.

,ii/wrez

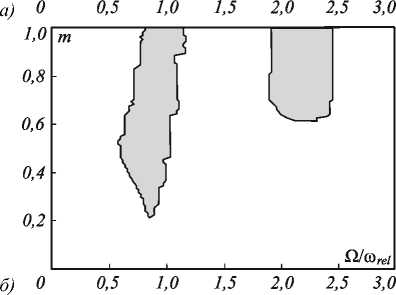
Рис. 2. Диаграмма устойчивости пространственнооднородных колебаний при параметрах σ = 0,1, γ = 0,001, a = 0,0001, r 0 = 5: δ = –0,1 (а), δ = –0,25 (б)

На рис. 2 а хорошо видно, что существует небольшая область параметров, локализованная вблизи частоты Ω=2ω rel , при которых режим колебаний пространственно-однородного профиля оказывается неустойчивым. На рис. 2 б присутствуют две области неустойчивости пространственно-однородных колебаний вблизи Ω 1 = 2ω rel и Ω 2 = 2ω rel . Области имеют вид характерных для параметрической неустойчивости языков синхронизации.

В области параметрической неустойчивости возможно формирование сложных регулярных оптических структур. При σ =0,1, γ =0,001, a =0,0001, r 0 =5, δ = –0,25, m =0,6, Ω =2 ω rel диаграмма экспонент Флоке в зависимости от волнового числа возмущения имеет вид, представленный на рис. 3.

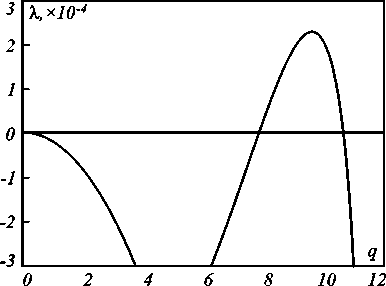
Рис. 3. Диаграмма экспонент Флоке в зависимости от волнового числа при σ = 0,1; γ = 0,001; a = 0,0001; r 0 = 5; δ = –0,25; m = 0,6; Ω = 2 ω rel

Из рисунка хорошо видно, что режим пространственно-однородных колебаний неустойчив по отношению к малым возмущениям, поскольку существует область волновых чисел с положительными показателями Флоке. Исходя из рис. 3, следует ожидать возбуждения на колеблющемся профиле пространственной структуры, аналогичной ряби Фарадея, с характерным волновым числом q max ≈9,7.

Результаты численного моделирования исходной модели (1) при выбранных параметрах были рассмотрены более подробно. Зависимость интенсивности оптического поля от времени в фиксированной точке пространства изображена на рис. 4.

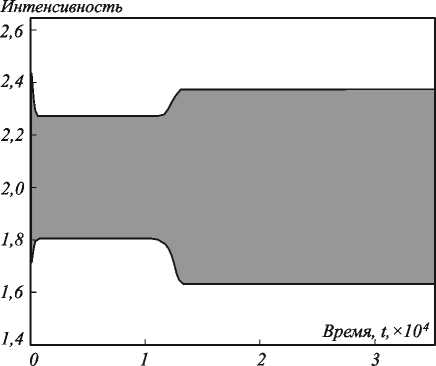
Рис. 4. Временная зависимость оптического поля в локальной точке при параметрах σ = 0,1; γ = 0,001; a = 0,0001; r 0 = 5; δ = –0,25; m = 0,6; Ω = 2 ω rel

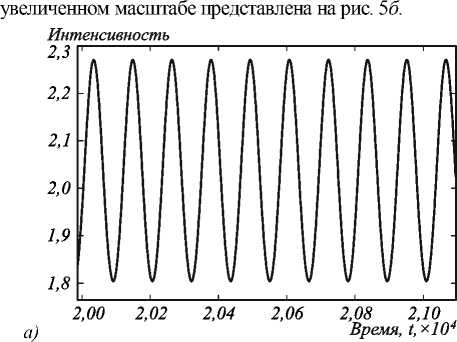
Можно выделить два этапа в формировании параметрически возбуждаемых оптических структур. На начальном этапе устанавливаются временные колебания квазиоднородного профиля. На рис. 5 а показан увеличенный фрагмент временной зависимости.

С течением времени неустойчивость колебаний однородного профиля приводит к возникновению пространственной моды, аналогичной ряби Фарадея. Нарастание данной неустойчивой моды приводит к формированию нелинейной оптической структуры. Зависимость интен- сивности от времени в случае развитой неустойчивости в

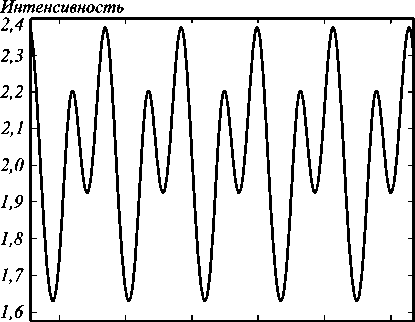
2,000 2,002 2,004 2,006 2,008 2,010

б)                                       Время, t.^lO5

Рис. 5. Колебания квазиоднородного профиля (а), колебания ряби Фарадея при параметрах σ = 0,1; γ = 0,001; a = 0,0001; r0 = 5; m = 0,6; Ω = 2ωrel (б)

На рис. 5 хорошо видно, что частота колебаний установившейся структуры вдвое меньше частоты колебаний однородного профиля, что находится в точном соответствии с другими результатами по ряби Фарадея, полученными для других физических моделей.

Моделирование в двумерном случае показало, что при выбранных параметрах реализуется структура в виде полос («страйпов») с дефектами (рис. 6 а ). В пространственном спектре доминируют гармоники с волновым числом q ≈ 10 (рис. 6 б ), что находится в хорошем согласии с волновым числом, предсказанным при помощи метода Флоке.

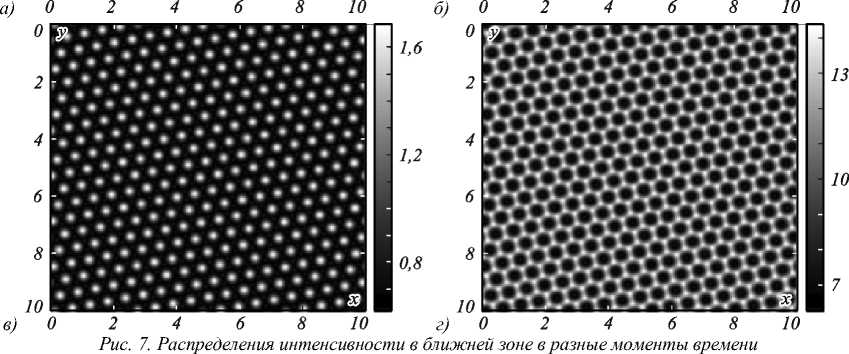
Численное моделирование показало, что возможно формирование также двумерных структур гексагональной формы. Пример такой структуры был получен численно при параметрах σ =0,1; γ =0,001; a =0,0001; r 0 =5; m =0,6; Ω =2 ω rel (рис. 7 а-г ).

Распределение интенсивности в дальней зоне, представленное на рис. 8а, показывает, что ха- рактерное волновое число сформированной гек- гласуется с результатами анализа Флоке сагональной структуры q ≈ 12,5, что хорошо со- (рис. 8б).

а) 0      2      4      6      8     10       б) -15 -10   -5    0     5    10   15

Рис. 6. Распределение интенсивности в ближней зоне (а) и пространственный спектр (б) при параметрах σ = 0,1; γ = 0,001; a = 0,0001; r 0 = 5; m = 0,6; Ω = 2 ω rel

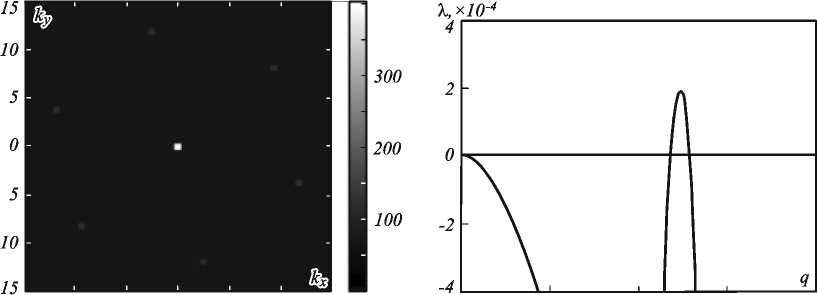
а) -15 -10   -5    0     5    10   15         б)   О         5        10        15       20

Рис. 8. Дальняя зона для гексагональной структуры (а) и диаграмма показателей Флоке (б)

При выборе параметров из области устойчивости диаграмм, изображённых на рис. 2 а-б , с помощью численного моделирования было подтверждено, что режим колебаний однородного профиля оказывается устойчивым, формирования пространственных структур не происходит. Любые малые возмущения режима колебаний пространственно-однородного профиля затухают с течением времени.

Заключение

Проведено исследование формирования оптических структур при параметрах из области устойчивости однородного решения для лазеров класса B в результате модуляции параметра накачки. Показано, что существуют небольшие области параметров (при частоте модуляции накачки, близкой к частоте релаксационных колебаний или к её удвоенному значению), в которых периодическая модуляция параметра накачки приводит к формированию поперечных пространственно-временных структур. Проведённое численное моделирование показало, что в широкоапертурных лазерах динамического класса В параметрическая неустойчивость приводит к формированию страйпов (полос) и гексагонов. Характерные размеры возбуждаемых структур хорошо согласуются с результатами проведённого анализа Флоке.

Работа выполнена при поддержке Министерства образования и науки РФ, Государственного задания вузам и научным организациям в сфере научной деятельности (проект 3.5139.2017/БЧ), а также гранта РФФИ 16-32-60151 мoл_a_дк.