Формирование пространственного воображения через решение задач на воображаемых чертежах

Развитие пространственного воображения учащихся - одна из главных задач школьного курса геометрии. Решение данной задачи обычно связывается с курсом стереометрии, изучаемым в 10-11-х классах. Однако заметно, какие огромные трудности появляются у школьников в начале изучения курса стереометрии, - ребята фактически " не наблюдают в пространстве". Удивляться этому не приходится. Ведь пространственной фантазии необходимо преднамеренно формировать и совершенствовать. И учиться этому необходимо заранее, в начале средней школы( а даже и в начальной).

При исследовании курса планиметрии нужно объяснять главные факты стереометрии. Например, рассказывая о плоских фигурах, вводить сведения о свойствах пространственных тел. Таким образом, основная мысль состоит в том, чтоб вводить учащихся с пространственными объектами до такого, как станет дано их формальное и серьезное определение.

Но до этого чем приступать к изучению стереометрии, что в соответствии с действующей программой по геометрии разрешено делать в 7-м классе, в 5-6х классах целесообразно готовить учащихся к восприятию стереометрического материала. Такая подготовка может содержаться в решении системы задач, включающей задачи на проекционном чертеже куба и его развертке.

Сформулируем задачу: определить как выглядит на чертеже куба линия, которая имеет заданный проекционный чертеж.

Ответом является рисунок с изображением искомой линии на чертеже куба.

Обязательно решается и обратная (более легкая) задача: определить, что представляет собой проекционный чертеж линии, которая данным образом изображена на чертеже куба.

Рассмотрим теперь эту задачу подробнее. Проекционный чертеж куба имеет три вида (спереди, слева и сверху), которые располагаются по правилам черчения (рис. 1). Чертеж куба - это хорошо всем известное его изображение на плоскости, один из вариантов которого представлен на рис.2.

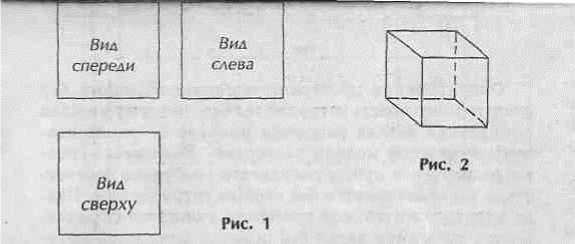
Итак, задача. Задан проекционный чертеж куба (рис. 3). Определить на чертеже куба выделенную (жирную) линию.

Ответ. Такой линией является линия, изображенная на рис. 4.

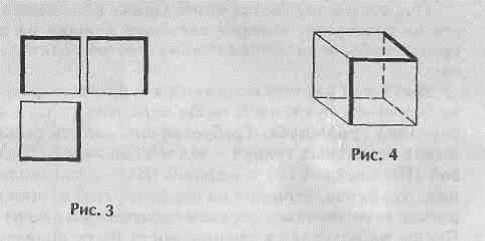
Приведем несколько заданий по данной теме (аналогичные задания легко составить самостоятельно). Каждую линию зададим соответствующим изображением на проекционном чертеже (рис. 5,а) и на чертеже куба (рис. 5,б).

Заметим, что в случае решения основной задачи позиция а) на рисунке является заданием, а позиция б) - ответом. В случае решения обратной задачи наоборот: позиция б) - на рисунке будет служить заданием, а позиция а) -ответом.

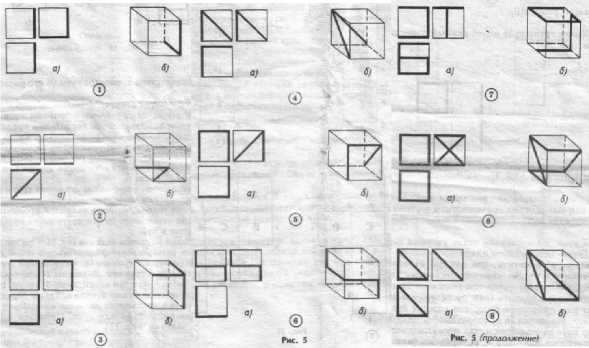
Остановимся теперь на содержании работы по обучению решению таких задач. Разумеется, первое замятие в 5-м классе не следует начинать с решения приведенных выше задач. Необходимо провести подготовительную работу, которую можно разделить на следующие этапы.

1-й этап. Ученики делают из бумаги модель куба. На этой модели изучаются элементы  куба:  вершины,  ребра  и грани. При этом рассматриваются следующие вопросы:

• 1)    Что представляет собой каждый элемент?

• 2)    Сколько элементов каждого типа?

• 3)    Что является границей двух элементов одного типа?

• 4)    Сколько и каких элементов «более низкого порядка» содержат в себе элементы «более высокого порядка»?

2-й этап. Ребята строят в тетради плоское изображение куба (чертеж куба -рис. 6); отмечают буквами вершины; учатся показывать и записывать все элементы куба по чертежу.

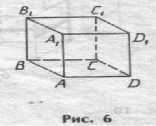
3-й этап. На бумажной модели куба определяются его виды: спереди, слева и сверху. Вводится понятие проекционного чертежа. На этом чертеже изображаются элементы куба и решаются простейшие задачи. Приведем примеры некоторых из них.

• 1.    Какая из вершин куба имеет данный проекционный чертеж (рис. 7)?

  

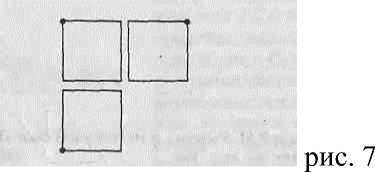
• 2.    Какое ребро куба имеет данный проекционный чертеж (рис. 8)?

Ответ: вершина A 1

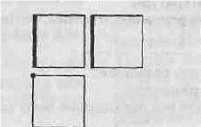
Рис. 8

Ответ: ребро ВВ 1

При этом обязательно решаются и обратные задачи: как выглядит на проекционном чертеже тот или иной элемент куба.

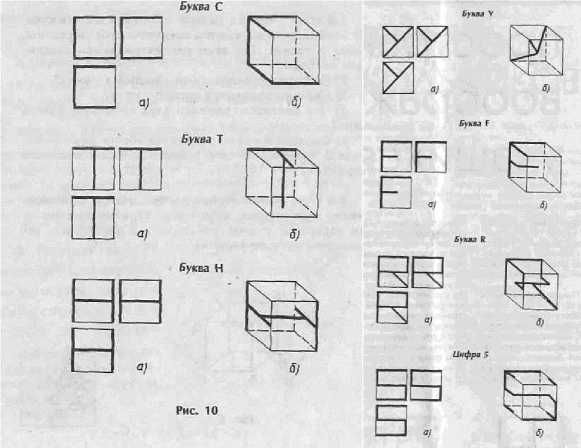
4-й этап. На последнем этапе ученики переходят к решению задач общего плана. Интересно отметить, что данные задачи можно представить в весьма «привлекательном» виде. Например, с большим интересом учащиеся занимаются составлением алфавита (как русского, так и латинского) или цифрового ряда, где каждая буква (или цифра) - это линия (или совокупность линий), которая на кубе на всех трех видах проекционного чертежа смотрится как одна и та же буква (или цифра). Подавляющее большинство таких задач было не только решено, но и составлено самими учащимися. В приведенных ниже примерах (рис. 10) на линию (или совокупность линий) накладывалось условие минимальности ее длины, поэтому линия может проходить не только по поверхности куба, но и внутри него.