Формирование псевдослучайных сигналов с управляемыми корреляционными характеристиками на основе систем с динамическим хаосом

Рассматриваются формирователи псевдослучайных сигналов с управляемыми статистическими характеристиками на основе нелинейных систем с динамическим хаосом. Показано, что оптимизации параметров временной дискретизации обеспечивает улучшение корреляционных характеристик и распределений вероятностей реализаций псевдослучайных сигналов. Исследовано влияние квазирезо-нансных управляющих воздействий на погрешности восстановления параметров систем Лоренца и Чуа в условиях действия комплекса шумов.

Формирование новых носителей информации для современных систем связи на основе эффектов хаотической динамики является актуальной задачей, выдвигаемой требованиями практики [1]. Известен целый ряд нелинейных систем с динамическим хаосом, порождающих хаотические сигналы. Системы Лоренца и Чуа являются в настоящее время наиболее широко исследованны- ми и реализованными в виде специализированных интегральных микросхем [1]. Управляющие воздействия на параметры систем с хаотической динамикой изменяют статистические характеристики формируемых ими сигналов. Одним из эффективных видов управляющих воздействий являются квазирезонансные воздействия [3].

Цель работы состоит в разработке метода и средств управления корреляционными характеристиками формирователей псевдослучайных сигналов на основе систем Лоренца и Чуа.

Система Лоренца была изначально получена при исследовании турбулентности и анализе конвективного движения [1]:

X = -aX + GY, Y = rX - Y - XZ,

. (1)

Z = -bZ + XY,

где X , Y , Z – переменные системы, r ,σ, b – параметры системы Лоренца.

Система Чуа описывает динамику автономной схемы, поведение которой становится хаотическим при определенных значениях параметров α , β [1]

X = a(Y - h(X)), Y = X - Y + Z, *

Z = -PY,

где кусочно-линейная аппроксимация ВАХ нелинейного элемента имеет вид:

bX + a - b , X >  1,

h ( X ) = ^

aX ,|X| <  1,

bX - a + b , X < - 1.

Для обеспечения воспроизводимости статистических характеристик формирователей хаотических сигналов необходимо использовать их цифровые реализации на основе процедур численного интегрирования систем дифференциальных уравнений (1)-(2). Поэтому, практи- чески важным является исследование влияния параметров временной дискретизации на корреляционные характеристики реализаций сигналов, порождаемых нелинейными системами с хаотической динамикой [2].

Оценку изменения шага временной дискретизации Δt по отношению к периоду T ₁ квазирезо-нансных колебаний около состояний равновесия динамических систем будем проводить по параметру K = T 1 / At . Аналитическое определение диапазона изменения параметра K при формировании псевдослучайных сигналов на основе систем Лоренца и Чуа выполнимо на основе анализа решений уравнений систем (1), (2), линеаризованных в окрестностях точек их устойчивого и неустойчивого равновесия [4].

Для системы Лоренца это точки C o ( 0,0, ( r - 1 ) ) и C _h2 = ± X oi , ± Y , Z _Oi , ( X oi = Y 01 = V ^b ( ^{r -} 1 ) , ^Z oi = ^{r -} 1 ) ; для системы Чуа - точки P o ( 0,0,0 ) и P _x2 = ( ± X 02 ,0, + Z 02 ) , где X 02 = Z 02 = ( b - a ) / ( b + 1 ) .

Спектры сигналов, полученные на основе решений линеаризованных систем уравнений Ло- ренца для характерных значениях параметров системы приведены на рис. 1.

Спектры, приведенные рис. 1-2, позволяют оценить верхние граничные частоты формируемых сигналов по уровням, соответствующим 95% энергии сигналов систем Лоренца или Чуа. Полученные оценки верхних граничных частот позволяют обосновать рекомендации по выбору параметра K при формировании псевдослучайных сигналов, порождаемых системами Лоренца и Чуа.

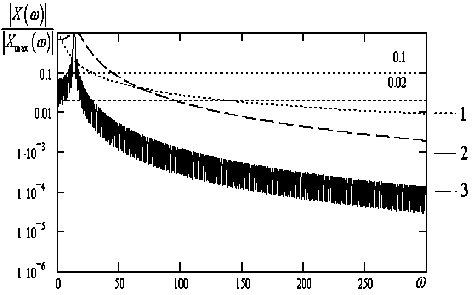
Рис. 1. Спектры сигналов линеаризованной системы Лоренца при r = 28 , ст = 10, b = 8/3 : 1; 2 - в окрестности C 0 ; 3 - в окрестности C 1 2

Спектры аналогичных сигналов, формируемых на основе системы Чуа, приведены на рис. 2.

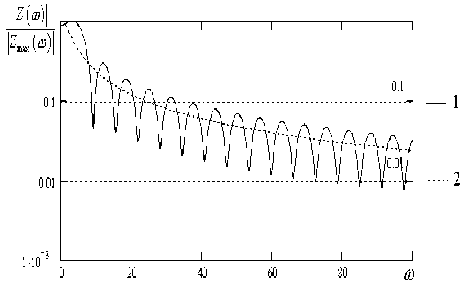
Рис. 2. Спектры сигналов линеаризованной системы Чуа при а = 9 ,8; Р = 110/7 : 1 - в окрестности P , ₂ ; 2 - в окрестности P 0

Диапазоны изменения K , полученные по аналитическим оценкам верхних граничных частот при вариации параметров систем, в работе сопоставлены с экспериментальными результатами, полученными путем математического моделирования систем с динамическим хаосом. Диапазон изменения K оценивался путем моделирования систем (1)-(2) при вариации начальных условий. Установлено, что для системы Лоренца при r = 28, о = 10, b = 8/3 аналитическая оценка K _A = 17,3…21,9; а по результатам моделирования K _M = 17,1…21,5; для системы Чуа при а = 9,8; в = 100/7 аналитическая оценка K _A = 39,6...41,0 а по результатам моделирования – K M = 39,4…42,2 [6].

Установленное качественное влияние параметра временной дискретизации K систем (1)-(2) на характеристики формируемых сигналов делает необходимым определение количественной взаимосвязи параметров временной дискретизации со статистическими характеристиками сигналов, формируемых на основе систем Лоренца и Чуа. Одной из основных характеристик хаотических сигналов является их автокорреляционная функция (АКФ), определяемая по реализациям сигналов систем (1)-(2) при вариации параметров систем.

Изменение АКФ сигналов, формируемых системами (1)-(2) оценивается по нормированным интервалам т(9)/т0 (9) до первого пересечения корреляционными функциями уровней 9 = 0,8; 0,6; 0,4; 0,2; т(9). Значение 9 = 1/e соот ветствует интервалу корреляции, по истечении которого происходит падение корреляционной функции в e раз по сравнению с максимальным значением, значение θ = 0 соответствует интервалу корреляции, определяемому по первому пресечения корреляционной функцией нулевого уровня, (см. рис. 3); т0 (9) - интервалы корреляции при K = 200 , выбранном в пределах аналитически определенного диапазона значений K [4].

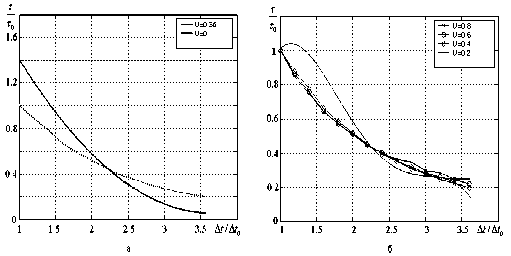
Рис. 3. Зависимости интервалов корреляции реализаций X системы (1): а - т ( е ) / т₀ ( е ) и т ( 0 ) / т ₀ ( 0 ) , б - т (0 , 8)/ т о ( 0 , 8 ) , т (0,6)/ т о ( 0,6), т (0,4)/ т о ( 0,4 ) , т (0,2)/ т о ( 0,2 )

Установлена взаимосвязь параметра К с динамическими характеристиками формируемых сигналов. При уменьшении параметра К временной дискретизации сокращаются интервалы корреляции сигналов, формируемых на основе систем Лоренца и Чуа с хаотической динамикой. Поэтому, параметры временной дискретизации при формировании псевдослучайных сигналов на основе систем с хаотической динамикой должны выбираться в пределах

^K min <  ^K <  ^K max , (3)

где нижняя граница диапазона изменения Kmin определяется максимальным значением шага временной дискретизации, при превышении которого фазовые траектории выходят за пределы ограниченной области фазового пространства, занимаемой странными аттракторами систем (1) и (2). Верхняя граница диапазона изменения Kmax ограничена значением шага временной дискретизации, при котором приращение переменных при численном интегрировании становится соизмеримым с погрешностью, вызванной конечной разрядностью вычислителя [5].

Важной особенностью нелинейных систем с динамическим хаосом является возможность смены регулярного режима хаотическим при квазирезонансных воздействиях на параметры систем [5]. Для формирования сигналов с воспроизводимыми статистическими характеристиками актуальным является решение задачи перевода нелинейных систем с динамическим хаосом из режима с преобладанием регулярной моды в режим с преобладанием хаотический моды. Сокращение интервалов корреляции сигналов, формируемых на основе систем с динамическим хаосом возможно путем введения управляющих воздействий на параметры системы. Эти воздействия должны обеспечить энергетическое преобладание моды, отвечающей за хаотическое поведение.

На основе анализа динамики системы Лоренца в окрестностях состояний равновесия предложены управляющие воздействия на параметры системы (1), определяемые знаком текущего отклонения переменных системы от состояния равновесия C ₁₂ [3]:

f(t) = sgn[(X - X01 )(Y -X)] , fr (t) = sgn (Y - Y01 ) , fb(t) = sgn ( Z - Z01 ) .

Управляющие воздействия вида (4) модифицируют исходную систему нелинейных дифференциальных уравнений Лоренца. За счет этой модификации происходит изменение динамики системы. По реализациям сигналов, формируемых системой (1) при квазирезонансных воздействиях (4) определены АКФ и интервалы корреляции. При использовании квазирезонансных воздействий на параметр r системы (1), нормированные интервалы корреляции сигналов X,Y,Z равны т(0)/т0(0) = 0,08...0,55; т(e)/t0(e) = 0,74…4,3 при глубине модуляции 0,1 ≤M ≤0,2 Воздействия на параметр b обеспечивают следующие значения нормированных интервалов т (0)/т0 (0) = 0,1^0,33, т (e) / т0 (e) = 0,69^4,5 при 0,8 < M < 0,9. Применение квазирезонанс-ных воздействий вида (4) на параметр σ системы (1) малоэффективно для сокращения интервалов корреляции формируемых псевдослучайных сигналов. При квазирезонансных воздействиях на параметры системы (1) интервалы корреляции формируемых сигналов сокращаются не менее, чем на порядок по сравнению с сигналами в отсутствии воздействий.

Новым эффективным способом управления поведением нелинейных систем с динамическим хаосом, позволяющим обеспечить требуемое изменение корреляционных функций формируемых псевдослучайных сигналов, являются предлагаемые квазирезонансные воздействия на параметры временной дискретизации, для системы Лоренца имеющие вид [6]:

X i + 1 = X i ⁺ ti ( - ° X i ⁺ ° ^Y i )

• * Y + i = Y, + t i ( rX , - Y i - X , Z , ) , (5) _ Zm = Z i + t i ( - bZ i + X i Y )

где t i = A t ( 1 + Mf i-1 ) , f_{t - 1} - временная функция

⎛Xi ⎞ управляющего воздействия, fi—i = sgn -лт ± a , ⎝X ⎠ a= X/ X01 , Δt – начальная величина шага. Отметим, что при этом пределы изменения ti = At (1 + Mfi-1) должны выбираться с учетом условия (3).

При использовании квазирезонансных воздействий на параметры временной дискрети- зации, нормированные интервалы корреляции сигналов, формируемых на основе (1), равны т(0)/т0(0) = 0,08^0,25; т(e)/т0 (e) = 0,25^0,3 при значениях глубины модуляции параметра временной дискретизации 0,33…0,5 ≤ M ≤ 0,75…0,8; 0,89 ≤ M ≤ 0,9…0,91 соответственно. Модуляция параметров временной дискретизации на основе квазирезонансных воздействий позволяет сократить интервалы корреляции сигналов не менее, чем в 20 раз по сравнению с сигналами в отсутствии воздействий. Поэтому квазирезонансные воздействия на параметр временной дискретизации системы Лоренца являются более предпочтительными по сравнению с квазирезонансные воздействиями на параметры системы.

Выводы

• 1.    Нелинейные системы с динамическим хаосом являются перспективным средством формирования псевдослучайных сигналов с управляемыми корреляционными характеристиками.

• 2.    Управление корреляционными характеристиками сигналов, формируемых системами Лоренца и Чуа, следует проводить путем выбора параметров временной дискретизации в пределах диапазонов, определяемых неравенством (3).

• 3.    Квазирезонансные управляющие воздействия на параметры систем с динамическим хаосом и параметры их временной дискретизации являются эффективными средствами сокращения интервалов корреляции псевдослучайных сигналов, формируемых на основе системы Лоренца.

• 4.    Квазирезонансные воздействия на параметры r и b системы Лоренца позволяют сократить интервалы корреляции псевдослучайных сигналов не менее, чем на порядок. Управляющие воздействия на параметры временной дискретизации дают двукратный выигрыш в сокращении интервалов корреляции по сравнению с квазире-зонансными воздействиями на параметры системы Лоренца.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант РФФИ №06-08-00848-а).