Формирование пучков Бесселя вихревыми аксиконами
Автор: Скиданов Роман Васильевич, Ганчевская София Владиславовна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.38, 2014 года.
Бесплатный доступ
Рассматривается формирование пучков Бесселя вихревыми аксиконами с разными топологическими зарядами структуры. Приводятся результаты вычислительных и натурных экспериментов.
Пучок бесселя, вихревой аксикон, топологический заряд
Короткий адрес: https://sciup.org/14059263
IDR: 14059263
Текст научной статьи Формирование пучков Бесселя вихревыми аксиконами
Пучки Бесселя имеют ряд свойств, которые определяют широту их использования: распространяются на некотором конечном отрезке без дифракции [1]; образуют световую полость, замкнутую по двум или трём координатам, в зависимости от условий фокусировки [2]; восстанавливают свою структуру после прохождения препятствия [3–5]; обладают орбитальным угловым моментом [6, 7].
Формировать пучки Бесселя можно с помощью ак-сикона [11], амплитудной цифровой голограммы [2], фазового дифракционного оптического элемента (ДОЭ) [12]. В [13] предложен элемент, который должен формировать пучки Бесселя с максимальной эффективностью. При этом в работах, посвящённых формированию пучков Бесселя, как правило, подразумевают, что формируется не пучок Бесселя, а его аппроксимация, которая похожа на пучок Бесселя, в небольшой локальной области и при распространении на коротком отрезке. Пучки Бесселя нашли широкое применение в оптической микроманипуляции [14–18]. Их использование для оптического захвата, перемещения и вращения микрообъектов определялось такими важными свойствами пучков Бесселя, как самовосстановление после препятствия [15, 16] и наличие орбитального углового момента. Орбитальный угловой момент пучка Бесселя растёт с увеличением его порядка. Существует ряд работ, в которых рассматривается формирование разными способами пучков Бесселя высоких порядков (порядок >> 10) [18, 19]. При этом возникают проблемы, связанные с технологическими ограничениями как пространственных модуляторов света [18], так и дифракционных оптических элементов на оптических подложках [19]. В результате формируемые пучки становятся с ростом порядка всё менее похожими на пучки Бесселя. Актуальной также в настоящее время является задача формирования суперпозиции пучков Бесселя в нулевом порядке дифракции [20]. Но предложенный в [20] метод будет плохо работать при близких константах распространения пучков Бесселя.
В настоящей работе рассматривается возможность формирования пучков, близких по структуре распределения интенсивности и фазы к пучкам Бесселя, с помощью вихревых аксиконов, содержащих топологический заряд структуры. По сути, такие элементы являются промежуточными между спиральными бинарными ак-сиконами и элементами, предложенными в [13]. Более того, и спиральный бинарный аксикон, и элемент [13] являются частными случаями рассматриваемых ДОЭ. В результате формирование пучков Бесселя одного порядка может быть осуществлено с помощью дифракционных оптических элементов, имеющих совершенно разную по структуре фазовую функцию, что позволит формировать на оптической оси суперпозиции пучков Бесселя с близкими константами распространения. Также предлагаемые элементы могут оказаться полезными при формировании пучков Бесселя высоких порядков, т. к. при их формировании происходит суммирование топологических зарядов структуры аксикона и топологических зарядов отдельных зон. Сочетание этих возможностей будет полезным при формировании световых пучков, предназначенных для вращения микрообъектов в разреженных средах.
1. Вихревые аксиконы
В [21] описываются дифракционные оптические элементы нового типа, которые имеют функции пропускания вида
т( r, ф) = —[exp (im^ + exp (im 2ф)] +
1 2 (1)
2. Моделирование
+ 2 [exp (im2ф) - exp (im^)] sgn [cos (2nvr + nф)], где m1, m2 – номера дополнительных вихревых составляющих, r, φ – полярные координаты, ν – пространственная несущая частота, n – топологический заряд бинарного дифракционного аксикона, который является основой структуры этого ДОЭ. С точки зрения геометрии ДОЭ с такой функцией пропускания выглядит как дифракционный бинарный аксикон, у которого в выступах записана вихревая составляющая m1, а во впадинах – вихревая составляющая m2, при этом расположение этих зон таково, что в ближней зоне также может формироваться световое поле с топологическим зарядом n. Будем в дальнейшем называть топологический заряд n топологическим зарядом структуры. В настоящей работе будем рассматривать элементы, у которых m1 = m2 = m, но при этом существует дополнительный поворот на π/m для разделения зон. Такие элементы, как было показано в [21], формируют пучки, очень похожие по распределению интенсивности на пучки Бесселя. Однако из-за общего характера работы [21] в ней подробно не рассматривался процесс формирования пучков Бесселя такими элементами. Формула (1) превращается для таких элементов в
т ( г , фф = 2 [ exp ( гтфф^ exp ( im ( ф + п ) ) ] +
+ 2 [ exp ( гтфф - exp ( im ( ф + п ) ) ] sgn [ cos ( 2 пи г + п ф ) ] .
Такой элемент при топологическом заряде структуры 0 очень похож на вихревой аксикон, предложенный в [13]. Визуально отличия видны только в центре элемента. Ширина линий же на краю элемента практически одинакова, и отличия можно обнаружить только при точном измерении. Как указывалось в [21], с помощью разных сочетаний топологических зарядов структуры и зон можно рассчитать фазовую функцию бесконечного количества элементов, каждый из которых будет формировать пучок с амплитудно-фазовым распределением, близким к пучку Бесселя.
В дальнейшем будем считать, что если на некотором отрезке пучок близок по амплитудно-фазовому распределению к пучку Бесселя (СКО < 10%), то он является некой аппроксимацией пучка Бесселя. Для краткости такие пучки будем называть пучками Бесселя.
В качестве эталона для сравнения будем использовать изображения со сформированным распределением интенсивности по функции Бесселя 7n2 ( а г ) , где параметр α подбирается таким образом, чтобы масштаб распределения интенсивности совпадал с масштабом пучка, который был получен путём численного моделирования дифракции на вихревых аксико-нах. На рис. 1 приведены два использованных эталонных изображения.

-
а) б)
Рис. 1. Изображения эталонных распределений интенсивности в пучках Бесселя 1-го (а) и 5-го (б) порядков
Моделирование дифракции на вихревых аксико-нах осуществлялось с помощью преобразования Френеля. Для некоторых из элементов распределение интенсивности было получено также с помощью интеграла Кирхгофа. Но т.к. существенных отличий в распределении интенсивности по сравнению с преобразованием Френеля выявлено не было, решено было интеграл Кирхгофа в моделировании не использовать. Для моделирования был выбран отрезок распространения исходя из двух условий:
-
1) дальний конец отрезка не должен превышать Rk / а где R — радиус вихревого аксикона, а - параметр функции Бесселя, k – волновое число;
-
2) на ближнем конце отрезка должно выполняться условие параксиальности, чтобы можно было использовать преобразование Френеля. Первое условие даёт при радиусе вихревого аксикона в 2,5 мм, длине волны 532 нм, α = 62831 максимальное расстояние 0,44 м. Из условия параксиальности следует, что правильное мо-
делирование с помощью преобразования Френеля будет на расстоянии более 0,25 м. В результате было принято решение слегка отступить от этих границ, и исследование формирования пучков Бесселя проводилось на отрезке от 0,3 м до 0,4 м. На рис. 2 представлен

в пучке Бесселя 1-го порядка на расстояниях
0,3 м (а), 0,33 м (б), 0,35 м (в), 0,38 м (г), 0,4 м (д)
Среднеквадратичное отклонение определялось по формуле
N2 8=^эт) Nn^ £1(I*- I”),
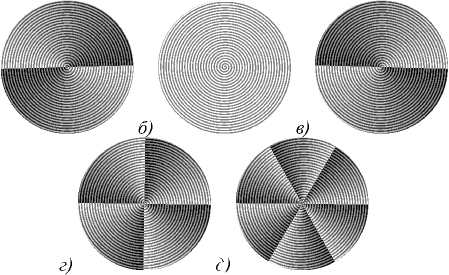
где Iij – значение интенсивности в ij пикселе изобра- жения, полученного в результате моделирования, Iijэт – значение интенсивности в ij пикселе эталонного изображения, N – размерность изображения. В качестве исследуемых распределений интенсивности, формируемых вихревыми аксиконами, были выбраны пучки Бесселя 1-го и 5-го порядков. Для формирования пучка Бесселя 1-го порядка были использованы элементы, приведённые на рис. 3.
а)
д)
Рис. 3. Вихревые аксиконы (а, в, г, д) и винтовой аксикон (б), формирующие пучок Бесселя 1-го порядка
В табл. 1 приведены значения полученных ошибок формирования пучка Бесселя 1-го порядка на отрезке от 0,3 м до 0,4 м разными вихревыми аксиконами.
В последней строчке в табл. 1 стоят средние величины СКО. Как видно, величина СКО изменяется весьма незначительно как с расстоянием, так и с видом элемента. Для визуальной оценки совпадения распределения интенсивности формируемого светового пучка и эталонного распределения рассмотрим центральное сечение распределения интенсивности, формируемого элементом с n = 0 и m = 1 на расстоянии 0,33 от элемента (максимальное для этого элемента СКО). На рис. 4 приведены центральные сечения для эталонного распределения интенсивности (рис. 4а) и сформированного распределения интенсивности (рис. 4б).
Табл. 1. СКО формирования пучка Бесселя 1-го порядка разными вихревыми аксиконами на отрезке от 0,3 м до 0,4 м
|
Расстояние, м |
n = 0, m = 1 |
n = 1, m = 0 |
n = 2, m = -1 |
n = 3, m = -2, |
n = 4, m = -3 |
|
0,4 |
0,015 |
0,028 |
0,030 |
0,006 |
0,020 |
|
0,38 |
0,037 |
0,031 |
0,044 |
0,037 |
0,027 |
|
0,35 |
0,043 |
0,035 |
0,044 |
0,054 |
0,057 |
|
0,33 |
0,053 |
0,027 |
0,019 |
0,030 |
0,034 |
|
0,3 |
0,020 |
0,020 |
0,039 |
0,018 |
0,022 |
|
0,034 |
0,028 |
0,035 |
0,029 |
0,032 |
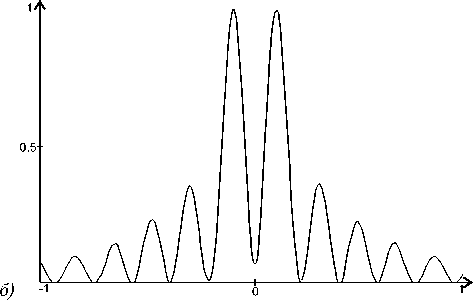
Рис. 4. Центральные сечения для эталонного распределения интенсивности пучка Бесселя 1-го порядка (а) и сформированного распределения интенсивности (б)
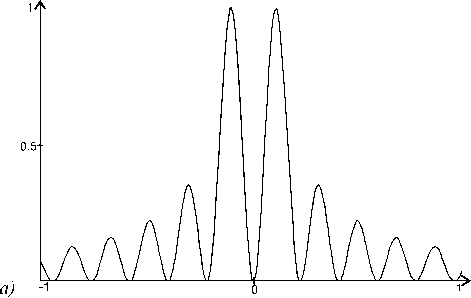
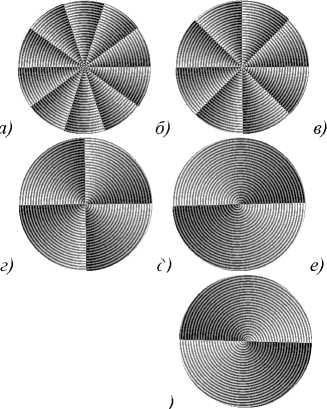
На рис. 5 приведены изображения распределения фазовой функции вихревых аксиконов, которые формируют пучок Бесселя 5-го порядка.
Как видно из рис. 4, отличия, которые можно визуально заметить, действительно невысоки и наблюдаются только на крайнем кольце. Для расширения диапазона исследуемых пучков Бесселя рассмотрим формирование пучков более высоких порядков, например пучка Бесселя пятого порядка.
д)
ж)
Рис. 5. Вихревые аксиконы(а, б, в, г, д, ж) и винтовой аксикон (е), формирующие пучок Бесселя 5-го порядка

В табл. 2 приведены значения полученных разными вихревыми аксиконами ошибок формирования пучка Бесселя 5-го порядка на отрезке от 0,3 м до 0,4 м.
Табл. 2. СКО формирования пучка Бесселя 5-го порядка разными вихревыми аксиконами на отрезке от 0,3 м до 0,4 м
|
Расстояние, м |
n = 0; m = 5 |
n = 1; m = 4 |
n = 2; m = 3 |
n = 3; m = 2 |
n = 4; m = 1 |
n = 5; m = 0 |
n = 6; m = -1 |
|
0,4 |
0,016 |
0,003 |
0,009 |
0,002 |
0,019 |
0,017 |
0,031 |
|
0,38 |
0,005 |
0,022 |
0,008 |
0,027 |
0,009 |
0,021 |
0,011 |
|
0,35 |
0,044 |
0,045 |
0,057 |
0,050 |
0,033 |
0,030 |
0,047 |
|
0,33 |
0,002 |
0,012 |
0,017 |
0,015 |
0,013 |
0,001 |
0,006 |
|
0,3 |
0,008 |
0,020 |
0,012 |
0,036 |
0,006 |
0,024 |
0,002 |
|
0,015 |
0,020 |
0,021 |
0,026 |
0,016 |
0,019 |
0,019 |
Как видно из табл. 2, величина СКО, так же как и в случае с пучком Бесселя 1-го порядка, изменяется весьма незначительно как с расстоянием, так и с видом элемента.
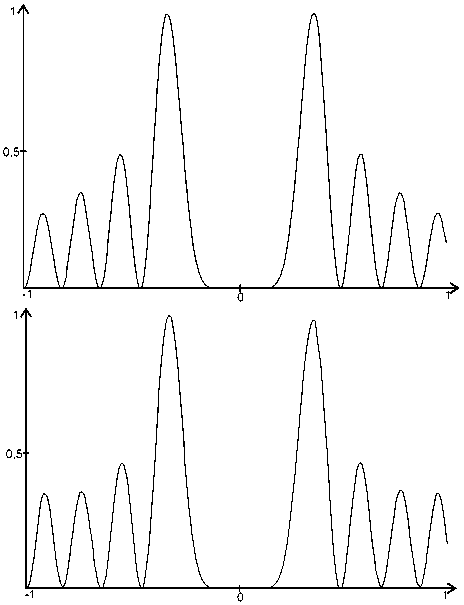
Для визуальной оценки совпадения распределения интенсивности формируемого светового пучка и эталонного распределения рассмотрим центральное сечение распределения интенсивности, формируемого элементом с n = 4 и m = 1 на расстоянии 0,35 от элемента (максимальное для этого элемента СКО). На рис. 6 приведены центральные сечения для эталонного распределения интенсивности (рис. 6а) и сформированного распределения интенсивности (рис. 6б).
Как видно из рис. 6, отличия, которые можно визуально заметить, действительно также невелики.
В табл. 1, 2 присутствует информация по величинам СКО формирования пучка Бесселя для элементов с m = 0, т.е. для бинарных винтовых аксиконов. Как видно из табл. 1, 2, величина СКО у винтовых акси-конов вполне сопоставима с величиной СКО вихре- вых аксиконов с ненулевым топологическим зарядом структуры. Для более корректного сравнения рассмотрим вихревой аксикон, построенный в соответствии с формулой (2), и элемент, описанный в [13], который, согласно [13], формирует пучок Бесселя с максимальной эффективностью. На рис. 7 представлены фазовые функции этих элементов.
а)
б)
Рис. 6. Центральные сечения для эталонного распределения интенсивности пучка Бесселя 5-го порядка (а) и сформированного распределения интенсивности (б)


а)
б)
Рис. 7. Фазовая функция элемента, предложенного в [13] (а), фазовая функция вихревого аксикона, рассчитанная по формуле (2) (б)
Как видно из рис. 7, элементы структурно почти не отличаются. Отличие заметно в центральной области, однако площадь отличающихся участков пренебрежимо мала по сравнению с площадью элементов. Вследствие этого формируемые этими элементами пучки также не будут существенно отличаться. Рассмотрим пучок, сформированный элементом, описанным в [13]. В табл. 3 приведены значения СКО для пучков 1-го и 5-го порядков, формируемых этим элементом.
Как видно из табл. 3, при сравнении с соответствующими данными в табл. 1 и 2 отличия действительно невелики. Более того, при формировании пучка Бесселя 5-го порядка элемент [13] формирует пучок даже с большей погрешностью, чем вихревой ак-сикон, рассчитанный по формуле (2).
Табл. 3. СКО формирования пучков Бесселя 1-го и 5-го порядков элементами [13] на отрезке от 0,3 м до 0,4 м
|
Расстояние, м |
1-й порядок |
5-й порядок |
|
0,4 |
0,041 |
0,020 |
|
0,38 |
0,012 |
0,027 |
|
0,35 |
0,013 |
0,022 |
|
0,33 |
0,031 |
0,037 |
|
0,3 |
0,011 |
0,006 |
|
0,022 |
0,23 |
3. Эксперимент
Распределения фазы элементов, рассчитанные по формуле (2), были сформированы на модуляторе Pluto Viz, который был установлен в оптической схеме, представленной на рис. 8.
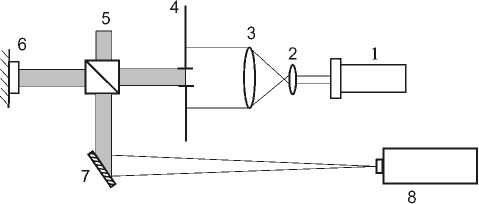
Рис. 8. Оптическая схема эксперимента по формированию пучков Бесселя: 1 – твердотельный лазер с длиной волны 532 нм, 2, 3 – коллиматор, 4 – диафрагма,
5 – светоделительный кубик, 6 – модулятор PLUTO VIS, 7 – зеркало, 8 – ПЗС-камера
ПЗС-камера была жёстко закреплена. Общая размерность модулятора составляет 1920×1080 пикселов. Фаза, сформированная на модуляторе, имела размерность 1024×1024 пиксела и формировалась в центре модулятора. Таким образом, точный размер сформированного фазового распределения составлял 8,2 мм. Перемещалась камера 8 так, чтобы сформировать на матрице изображение пучка Бесселя внутри отрезка от 600 мм до 800 мм от модулятора (с учётом того, что размер сформированного элемента на модуляторе почти в 2 раза больше размера моделируемых элементов). На рис. 9 представлены распределения интенсивности в пучке Бесселя 1-го порядка, сформированном вихревым аксиконом с n = 1, m = 0 ( а ), с n = 4, m = -3 ( в ), а также пучка Бесселя 5-го порядка, сформированного вихревым аксиконом с n = 5, m = 0 ( б ),

-го
Как видно из рис. 9, наблюдается качественное соответствие интенсивностей сформированных пучков Бесселя с интенсивностями пучков Бесселя, полученными в результате моделирования, что подтверждает возможность формирования пучков Бесселя вихревыми аксиконами с разными топологическими зарядами.
Заключение
Рассмотрено формирование пучков Бесселя вихревыми аксиконами. Методом вычислительного и натурного экспериментов показана возможность формирования пучков Бесселя, порядок которого определяется суммой топологических зарядов структуры вихревого аксикона и топологического заряда зон этого аксикона. За счёт этого формирование пучка Бесселя n-го порядка может быть осуществлено с помощью бесконечного количества вихревых аксиконов с разной фазовой функцией. Это расширяет возможности формирования суперпозиций пучков Бесселя, распространяющихся вдоль оптической оси и имеющих близкие параметры, такие как константа распространения, порядок. Предполагается использовать такие суперпозиции в задаче оптического вращения микрообъектов в разреженных средах, где необходимо выполнение двух условий, накладываемых на световой пучок: высокий орбитальный угловой момент и некольцевая структура пучка, что предположительно позволит избежать термического разрушения микрообъекта.
Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-19-00114).


