Формирование пучков в аподизаторе с квадратной зубчатой диафрагмой
Автор: Сизова Ирина Михайловна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.47, 2023 года.
Бесплатный доступ
Теоретически исследована трансформация профиля однородного монохроматического пучка с плоским фазовым фронтом после прохождения квадратного аподизатора, состоящего из зубчатой диафрагмы и пространственного фильтра, и при распространении за ним. Показаны основные отличия от случая круглой геометрии аподизатора. Рассмотрены роли формы углов квадратной зубчатой диафрагмы, фазы при дифракции Френеля, формы зубцов диафрагмы и отношения ширины зубцов к их высоте.
Дифракция, дифракционная оптика, компьютерная оптика, апертуры, аподизация
Короткий адрес: https://sciup.org/140300060
IDR: 140300060 | DOI: 10.18287/2412-6179-CO-1219
Текст научной статьи Формирование пучков в аподизаторе с квадратной зубчатой диафрагмой
Пионерской теоретической и экспериментальной работой по использованию аподизаторов с зубчатой входной диафрагмой (ЗД) для формирования в мощных лазерных системах пучков с плоской вершиной и заданным плавным переходом от плато к резко спадающим крыльям (платообразных пучков) считается работа Ауэрбаха и Карпенко [1]. По их утверждению, официальная история ЗД началась намного раньше, с предложения таких аподизаторов в 1978 г. для американской лазерной термоядерной установки Nova (частное сообщение). Упоминание о возможности применения ЗД встречалось и за 2 года до 1978 г. – в тезисах конференции [2] и 2 года позже [3]. Это направление аподизации получило широкое развитие и дальнейшее изучение [4, 5]. В большинстве работ и экспериментов речь шла о квадратных ЗД (включая [1]), а для круглых предлагались соответствующие поправки. Теоретическое рассмотрение делалось либо оценочно методом прямого и обратного Фурье-преобразований с применением теоремы о свертке в предположении дифракции Фраунгофера [1], либо упрощенными двухмерными расчетами параболического уравнения (ПУ) на сетке [4, 6].
Оптическая схема рассматриваемого аподизатора состоит из ЗД и пространственного фильтра (ПФ). В таком аподизаторе ЗД и сглаживает плато выходного пучка, и формирует профиль его крыльев.
В [7, 8] мы рассмотрели применение ЗД-ПФ в круглой геометрии аподизатора, в соответствии с задачами в гибридных фемтосекундных лазерных системах видимого диапазона [9– 13]. В предположении на входе ПФ у лазерного пучка плоского фазового фронта и радиальной симметрии амплитуды (Гаусс, однородный пучок) из известного точного решения ПУ было получено приближенное интегральное решение для поля на выходе ПФ, сводящее расчеты к вычислению однократного интеграла и позволяющее проследить за структурой полученного поля, подобрать для него адекватное аналитическое представление и разработать методы улучшения профиля пучка [14, 15]. Это представление позволяет аналитически рассчитать дифракционные искажения пучка за ПФ.
Здесь аналогичная методика расчета применена к аподизатору с квадратной ЗД. Особое внимание уделено различиям для круглой и квадратной ЗД.
Все расчеты делались с помощью программы Wolfram Mathematica.
1. Теоретическая модель
На рис. 1 показана схема аподизатора, состоящего из ЗД на входе и ПФ (фильтра нежелательных пространственных частот) в виде телескопа Кеплера с ограничивающей диафрагмой (ОД) в общем фокусе объектива и окуляра. ОД обрезает поперечную из-за ЗД структуру пучка. Полагаем на входе ЗД-ПФ монохроматическое поле с плоским фазовым фронтом.
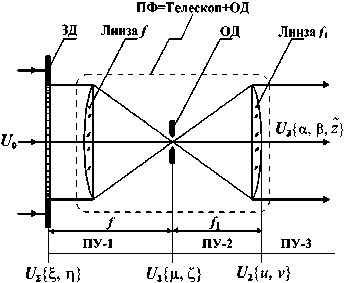
Рис. 1. Cхема аподизатора из ЗД и ПФ на базе телескопа Кеплера с ОД в общем фокусе объектива и окуляра.
Обозначены поля и их аргументы на границах ПУ и за ПФ
Поле в ПФ и за ним рассчитывается из интегральных решений ПУ (4πi / λ)(∂U / ∂z)+Δx,yU =0 в прямо- угольной декартовой системе координат {x, y, z} [16] (рис. 1; Δx,y – поперечный лапласиан, z – продольное направление, λ – длина волны излучения) и представлено в безразмерном по всем координатам виде. Решение U1 из ПУ-1 в фокусе телескопа (z = f) будет
U M Z , f ) _e Г.ц2 + Z2' — exp i ( - i о ) [ 4 no
JJ U z e - - , ц^+ y n ) d Z d n , (1)
где σ = a2 / λf – число Френеля ЗД в фокусе телескопа, амплитуды поля U1 и UΣ нормированы на максимум UΣ на входе ПФ; поперечные координаты {ξ, η} на входе ПФ (z =0), отсчитываемые от центра Σ ЗД, – на половину a внутренней части ЗД по краям зубцов; а координаты {μ, ζ} в фокусе ПФ (z = f) – по формулам ц — 2nxa / Xf; Z — 2nya / Xf.(2)
Тогда ограничение на (2) от ОД (2 x 0 ×2 x 0 ) будет
Цо — Z 0 — 2n ax о/ Xf.(3)
В (1) подставляем нормированное поле U Σ на входе ПФ, предполагаемое в виде
Uz — Uo(Z)Uo(n)exp [-i nc(Z2 +n2)],(4)
где U 0 (ξ) U 0 (η) – амплитуда U Σ в виде произведения одинаковых четных по ξ и η функций U 0 с максимумом 1, а фазовый множитель (4) учитывает прохождение первой линзы телескопа с фокусным расстоянием f. Линзу считаем абсолютно тонкой и совпадающей с плоскостью квадратной ЗД, симметричной по ξ и η; μ и ζ отсчитываем от центра квадрата ОД. Далее приведены расчеты для однородной амплитуды поля U 0 = 1. Обобщение на случай Гауссового пучка, как в [7, 8, 14, 15], полученных выводов не меняет.
Зубцы отверстия ЗД (будем далее говорить о зубцах именно отверстия для единообразия с зубцами в углах) полагаем одинаковыми, симметричными, одинаково расположенными на сторонах квадрата симметрично относительно их центров – рис. 2. Их безразмерные параметры равны l — L / a; h — H / a, (5)
где H и L – высота и ширина зубца отверстия.
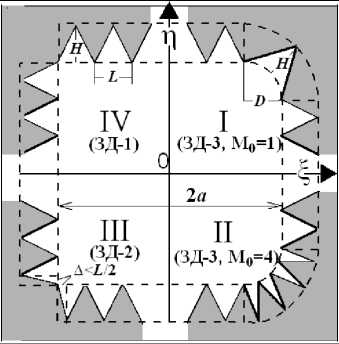
Отметим первое отличие круглой и квадратной ЗД. У круглой симметрия пучка за ЗД осевая порядка n (n – число зубцов). ОД обрезает поперечную структура пучка, возвращая ему входную радиальную симметрию. Из-за углов у квадратной ЗД и после обрезания ОД поперечной структуры пучок не восстанавливает форму в виде произведения одинаковых функций U (x, y) = U(x)U(y). Форма углов ЗД может влиять на детали выходного пучка. В описанном в [1] эксперименте в Ливерморской лаборатории [17] углы ЗД закруглены с зубцами по кругу. В [4, 5], судя по их картинкам, у металлической ЗД лазерной резки в углах зубцов нет, а у фотолитографической ЗД на стеклянной подложке в углах была сетка из скрещенных зубцов.
а)
б)
Рис. 2. (а) Варианты углов квадратной ЗД. В квадрантах III (ЗД-3) углы закруглены с равномерно вырезанными M 0 зубцами (от 0 до 5); показаны M 0 = 1 и M 0 = 4.
В квадрантах III-IV в углах нет зубцов и зубцы у углов смыкаются: в IV (ЗД-1) они симметричны, в III (ЗД-2) – нет (0 < Δ < L/2). Штриховыми линиями ЗД разбита для интегрирования в (1): на 5 частей в ЗД-1, на 13 – в ЗД-2, на 9 – в ЗД-3. (б) Определение формы ползубца по сторонам ЗД (не закрашен). Ордината отсчитывается от центра зубца
Рассмотрены 3 формы углов ЗД (рис. 2 а ): 2 варианта без зубцов и закругления (ЗД-1 и ЗД-2 в квадрантах III и IV) и с закруглением в четверть окружности, где вырезано разное число одинаковых симметричных зубцов, – как в [1, 17] (ЗД-3 в квадрантах I, II). У ЗД-1 зубцы у углов точно смыкаются (2 а равно целому числу L ). У ЗД-2 размеры а и L не согласованы и для смыкания в углах крайние зубцы несимметричны. У ЗД-3 в углах было от 0 (закругление без зубцов) до 5 зубцов. Форма зубцов (рис. 2 б ) бралась разной, в том числе разной по сторонам и в углах (если они там были). На схематическом рис. 2 а все зубцы треугольные. Подробно рассмотрен случай ЗД-1, дающий простой вид поля. Для ЗД-2, 3 рассчитаны поправки.
-
2. Поле на выходе аподизатора
-
2.1. Поле при аподизаторе с ЗД-1
-
Интегрирование в (1) с ЗД-1 дает для поля U 1
iU 1 ( ц , Z , f ) exp [- i ( ц 2 + Z 2 ) / 4 ло] / о — 1 1 + 1 23 , (6)
где I 1 – интеграл по квадрату 2 a ×2 a . При U 0 = 1 он равен (sinc( x ) = sin( x ) / x )
1 1 ( ц , Z ) = 4sinc ( ц ) sinc ( Z ) , (7)
а I 23 (μ, ζ) = I 2 (μ, ζ)+ I 3 (μ, ζ) – интегралы соответственно по верхнему с нижним и левому с правым прямоугольникам 2 a × H на рис. 2 а . I 2 (μ, ζ) = I 3 (ζ, μ) рассчитываются суммированием по пропусканию через все зубцы [18], и при U 0 = 1 каждый из них равен
I з ( ц ,0 =
1+h. sinc [Z 1 ф <^)/2l
= 4sinc(Z) f Ф©cos(ц^)---.L]
J1 sinc ( Z 1 /2 )
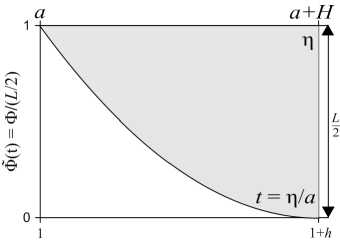
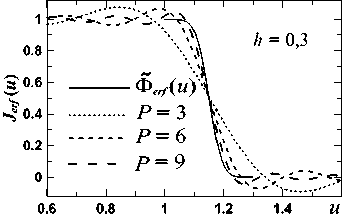
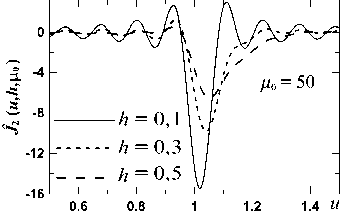
Ф Нормированную на максимум в (9) половину зубца Φ (t) (t = η или ξ; рис. 2б) назовем формой зубца. ОД обрезает колебательную структуру, обусловленную зубцами ЗД [1], и, очевидно, должна «убрать» зависимость (8) от l, т.е. обеспечить выполнение F (q) = sinc Г q Ф (t)] sinc (q) »1,0 <Ф( t) < 1, где q = ζl /2. Сравнив при Φ(t) ≤ 1 и разных q и h F(q) с 1 и интеграл в (8) с интегралом в предположении (10), мы получили, что F(q) – 1≤ 0,1 при q ≤ 0,75 и F(q) – 1 ≤ 0,01 при q ≤ 0,25. При q = 0,75 отличие интегралов – до 5 %, при q = 1 – до 9%, а при q = 1,5 возрастает до 20 %. Эти оценки не зависят от h. Т.е. вполне приемлемо ограничение q ≤ 1 – погрешность за счет (10) в (8) ниже 10 %. Отсюда вытекает ограничение на ОД (3) Цо =Zo < 2/1. (11) Условие (11) в 1,5 раза сильнее, чем ограничение на ОД в [1]. С учетом (10) получаем для поля U1 (6) в фокусе ПФ приближенное выражение iU1(ц, Z, f )exp [-i (ц2 + Z2) / 4nc] / 4g = = sinc ц sinc Z + 1+h sincц J Ф(t)cos(Zt)dt + 1+h + sincZJ Ф(t)cos(цt)dt которое подставляется как начальное в ПУ-2 на рис. 1 для расчета поля U2 на выходе ПФ. При (10) в (12) μ и ζ разделены в каждом слагаемом, а не во всей функции, как на входе ПФ. Из ПУ-2 поле на выходе ПФ (z = f + f1), с учетом набега фазы после линзы f1, будет Ho -U2(u,v, f + f1 )(п2 /4) = Jcos(цu)dцх xjiU1(ц,Z,f) exp(i5(ц2 + Z2))cos(ZV)dZ , G где к безразмерным координатам в фокусе (2) добавлены безразмерные координаты на выходе ПФ u = (f / af1) x; v = (f / af1) y, (14) а к безразмерным параметрам (3, 5) – параметр фазы 5 = (1 + f / f1)/(4nG). (15) Поле U2 (13) и его аргументы (u, v) (14) по сравнению с UΣ(ξ, η) дополнительно нормированы на коэффициент увеличения телескопа f / f1: U2 нормировано на поле U02f / f1, а аргументы – на поперечный размер пучка (af1 / f) в приближении геометрической оптики (ГО). Тогда U2(u, v) имеет платообразную форму с плато ≈ 1 и шириной ≈ 1 от центра; она симметрична и четна по u и v. Далее будем следить за u, v ≥ 0. Функция Φ и параметры h, μ0, δ (3, 5, 15) полностью определяют U2. Крылья U2 зависят от Φ, а детали плато – от h, μ0, δ. Как и с круглой ЗД [7, 8, 14], у U2 есть небольшие амплитудно-фазовые наросты на краю плато. В [1], согласно их данным, h = 0,25; l = 0,04; μ0=76, δ≈ 0,002; в [4] – h =0,17; l =0,05 и 0,033; μ0 = 15÷170. В расчетах будем ориентироваться на эти величины. Если в (13) (полагая μ0= ζ0) подставить (12), то получим для U2 -U2( U, V, f + fx) = J (v) J (u) -1 (v) I (u),(16) 2 цо I(u) = — Jcos(цu)e5" dц j" (t)cos(цt)dt,(17) п 01 2 цг, J(u) =— [sincц-cos(цu)e5ц dц +1(u),(18) п 0 где (18) хорошо описывает поперечный срез пучка (16) на плато по v. А произведение крыльев (17) I (u) I (v) в (16) вычитает из произведения (18) часть угловой структуры крыльев. Если положить 5 = 0, то интеграл, описывающий плато в (18), вычисляется [18] и дает (Si(x) – интегральный синус) J (u) = [Si(1 - u )ц0 + Si(1 + u )ц0 ] / п +1 (u). (19) Если в (16) положить μ0 →∞ и δ =0 (ГО), то -U2( u, v, f + f1) =[1, (u\,|v| < 1)] + + [(v|),(|u\< 1) n (1 < |v| < 1 + h)]+ (20) + [<ф (|u I), (| v| < 1)n (1 < |u| <1 + h)], т.к. при x → ∞ Si(bx) =(π /2) sign b [18] и lim (sin xy / y) = πδ ( y), где δ ( y) – дельта-функция [19]. У (20) квадратное плато 2×2, углы крыльев пучка полностью вырезаны в четверть круга и профиль крыльев по бокам совпадает с профилем Φ (u). В этом второе отличие круглых и квадратных ЗД: для круг- лых форма крыльев в приближении ГО совпадала с функцией Φ (u)/ u. При конечных μ0 вид (20) сглажен. Мы смотрели несколько видов Φ (t) в (12) – рис. 3. Часть Φ(t) взята из [8] – рис. 3а (треугольник, выпуклая и вогнутая параболы, косинус и треугольник со скосами острия и впадины). У треугольного зубца Φ (t) равно Ф l (t) = (1 + h -t)/h. И добавлены к этому (рис. 3б) еще зубец с профилем интеграла ошибок erf(x) [19] (c – крутизна спада) Фerf(t) = 2 + erf {c [1 - 2( t -1)/h ]/2} 2erf(c/2) , и прямоугольный зубец шириной 2 (1– с) (как в [4]) Ф rect (t) = 1 - c, 1 < t< 1 + h . а) б) Рис. 3. (а) Φ̃(t) при h = 0,6 из [8]. (б) Φ̃(t) (22, 23) при h = 0,3, где сплошные линии – модели зубцов ΦLmod (t) (см.(25)): для Φ̃erf (c = 6) l1 = 1,09, l2 = 1,21; для Φ̃rect (c = 1/3) l1 = 1,06, l2 = 1,34 Примеры J(u) (19) – срезов U2(u, v) (16) вдоль u при |v|< 1, когда [Si(μ0(1– v))+Si(μ0(1+v))] / π≈ 1, для Φ(̃ t) с рис. 3 и сравнение их с (20) показаны на рис. 4. Крылья (19) при 1 ≤ | u | ≤ 1+ h близки Φ (u). Чем больше μ0 и h, тем плато ближе к 1 и крылья – к Φ (u). Исследуем влияние μ0 и h на связь J (u) и I (u) с Φ (u). Интеграл ‘r X T=t - t 0 F (ц) = J f (‘)cos (ц ‘) d ‘ = t0 ‘ 1- ‘ 0 = cos(цtо) J f(tо +t)cos(цт)dt- (24) ‘1- ‘ о - sin (цtо) J f (tо +t)sin (цт) d t , 0 при μ → 0 приближенно равен (cos (μt) ≈ 1; sin (μt) ≈ μt) F (μ) ≈ I0 cos (μt0) – μ (I1– t0 I0) sin (μt0), где I0,1 – моменты 0 и 1 для f (t) от t0 до t1; а при μ→ ∞, опираясь на [20], F (μ) ≈ cos (μt0) f ʹ(t0) / μ2–sin(μt0) f (t0) / μ≈ – sin (μt0) f(t0) / μ. б) в) Рис. 4. J(u) (19) при разных P = μ0h для Φerf (22) при с = 6 (а); ΦTr (рис. 3а) (б) и Φrect (23) при с = 1/3 (в). Сплошные кривые – функции Φ(u). Штриховые кривые J(u) на (а) взяты при разных μ0; на (б, в) – при многих разных наборах μ0 и h из указанного диапазона (кривые с одинаковыми P слились) В [8] была исследована аналогичная (24) свертка с нулевой функцией Бесселя J0 вместо косинуса и показано, что для f (t) вида Φ на рис. 3 свертки хорошо воспроизводятся интегралами от похожей функции, имеющей с f (t) одинаковые нужные моменты и f (t0). В качестве такой функции удобно взять кусочно-линейную функцию. Расчеты при h ≤ 0,8 показали, что эта схема применима и к (24) для интеграла I(u) (17). Заменим (17) интегралом, где вместо Φ(t) стоит ΦLmod(t) – треугольный зубец с размерами l1 и l2 вместо 1 и 1+h (l2,1 = 1+I0 ± {3 [2(I1– I0)– I02]}½), сдвинутым вдоль t внутрь (l1 < 1) или наружу (l1 > 1). ΦLmod подбиралась из равенства с Φ её I0,1 и значения в начале интервала (l1 или 1). Выбор ΦLmod (t) продиктован простотой; можно взять функцию и другого вида. При l1 > 1 ΦLmod принимает вид Ф Lmod (‘) ={1,1 < ‘< 11} , l1< t< 12 При l1 < 1 левая граница по t у ΦLmod меньше, чем у Φ. Тогда при l1 ≤ t ≤ 1+h заменяется интеграл от f (t)= {1, l1 ≤ t ≤ 1}+{Φ̃ (t), 1 ≤ t ≤ 1+h} в (17) на интеграл от fmod (t)=(l2– t) /(l2– l1) при l1 ≤ t ≤ l2 (обе функции равны 1 при t = l1). Для (21) обе модели совпадают с (21). Для Φ̃p1,с l1> 1, для Φ̃p2,Tr l1< 1. Для (22) l1<(≥)1 при c < (≥) 2,17. Для (23) l1 < (≥)1 при c < (≥) 0,4. У плавных Φ (на рис. 3 это все, кроме ΦTr и (23)) функции ΦLmod (t) близки Φ(t). При изломах в Φ(t) отличие может быть даже качественным. Но важнее качество аппроксимации (17, 19) при замене Φ на ΦLmod. Для ФLmod интеграл (17) при 5 = 0 равен [18] Il mod (u) = -[Si (цо(1 - u)) + Si (цо(1 + u))] / п + J(12 ± u )Si (po( 12 ± u ))±[-( 11 ± u )Si (po( 11 ± u)) + ^--sin(M12 -li)/2)x (12 - 11)П Ц0 xSsin (ц0( 12+l1 ± 2 u )/2) а JLmod (u) в (19) равно (26) без первого слагаемого. Для плавных Φ (t) J(u) ≈ JLmod (u) при любых h и μ0, но вид их меняется: с ростом Р = μ0h крылья обоих J приближаются к Φ (u) (рис. 4а; все J ≈ JLmod). Для Φ (t) с изломами близкие при малых Р (на рис. 4в при Р =3) J расходятся с ростом Р: крылья JLmod (u) приближаются к ΦLmod (u), а у точной J (u) проявляются искажения, близкие изломам Φ (u) (рис. 4б, в). Разберем вид кривых на рис. 4. Перепишем I(u) (17) при 5 = 0 как I (u) = - j Ф (xh +1) п0 sin (цо(1 + h x + u)) + 1 + hx + u + sin (цо(1 + h x-u)) 1 + hx - u d x« 1 - , , sin (P(x- 5)) •'Ф(xh +1) dx , 0 (x-5 ) где χ =(t –1)/ h и s =(u –1)/h. Мы пренебрегли первым, заметно меньшим слагаемым в квадратной скобке (27), полагая u ≥ 1. В (27) появился параметр Р с рис. 4 P = ц0h. Для всех зубцов рис. 3, кроме Φp1, Φ(t), как и их ΦLmod(t), зависят лишь от χ. Поэтому (27) зависят лишь от P и s. Для Φp1 остается зависимость и от h. Тогда при данном P и Φ, зависящих лишь от χ , крыло пучка, описываемое J(u), имеет одинаковый вид от s ростом P у J и JLmod в крыльях проявляется отличие Φ и ΦLmod. Эти граничные P ≈ 5 ÷ 8 слегка зависят от Φ, а P, при которых спад J близок Φ, – десятки. Хотя и тогда некоторое отличие остается. Схожее поведение и у функций (19) для ΦP1(t), зависящей и от P, и от h. Здесь такая же картина примерно при тех же значениях P, но поведение J (u = sh + 1) (19) зависит отчасти и от h. Наличие параметра P и его роль в форме крыльев пучка на выходе ПФ – третье отличие для круглой и квадратной ЗД. Для круглой ЗД такого параметра нет. Если исходить из P ≥ 12 как условия приближения крыла J (sh +1) к Φ (sh +1) и отличия его от крыла для Jmod (sh +1), то вместе с (11) это будет H/L ≥ 6, что и фигурирует в [1] (по данным [1] P ≈ 19 и H/L= 6,25). Однако даже при бόльших P, когда крыло J(sh +1) близко Φ̃ (sh +1), а крыло Jmod (sh +1)– Φ̃Lmod (sh +1), отличие этих функций именно на спаде невелико. Оно проявляется на переходе от плато к крылу, внизу крыла и для зубцов с изломами типа ΦTr и (23) – в местах изломов. Поэтому при больших P зубцы должны быть плавной формы без дефектов, а при P ≤ 5 крылья пучка будут сглажены даже у простого треугольного зубца. Это видно в [4], где сравниваются крылья пучков с квадратным профилем зубцов и с профилем, подогнанным под супергаусс порядка 14, близкий (22) при h ≈ 0,17 и с ≈ 6,7. В обоих случаях у них H/L =5, h ≈ 0,17, и, полагая, что их угол дифракционной расходимости пучка отвечает x0 = λf /2a в (11), для него μ0=π и P меняется в диапазоне 2,5÷28,3. Итак, видно, что для квадратной ЗД-1, как и для круглой [7, 8, 14, 15], на выходе ЗД-ПФ образуется платообразный пучок с плавным переходом от плато к крыльям и профилем, при P ≤ 5 хорошо описываемым (19, 26) для модели треугольного зубца ΦLmod. Плавный профиль этого крыла можно подобрать под нужный вид. При P ≥ 12 профиль крыла близок Φ(sh +1); и тогда уже профиль зубцов ЗД надо подгонять под желательный профиль крыла. 2 .2. Поле при аподизаторе с ЗД-2 Оценим поправки к U2 в (16) при ЗД-2 (рис. 2а), также полагая падающее на ПФ поле однородным с плоским фазовым фронтом, δ =0 и срезом углов ЗД по прямым. У ЗД-2 зубцы в углах ỳже L /2. Обозначим Δ/a = kl /2, где 0< k< 1. Интеграл в (1) разбит на 13 частей. Интегрирование в квадрате 2a×2a дает (7), а вклад в (1) от боковых прямоугольников (4 по 2(a – Δ)×H и 8 по Δ×H) даст для I3(μ, ζ) вместо (8) J(u) = [Si(1 - u)ц0 + Si(1 + u)ц0 ] / п +1(u) ® «[Si( Ps)/п +1/2] +1 (u = sh +1). 13 (ц, ^, k) = 4 sinc(Z) x Расчеты это подтверждают (рис. 4): J(u) (19) (для u ≥ 0), представленные на рис. 4б, в от аргумента s, почти совпадают при одинаковых P. При P малых J и JLmod близки и их крылья не повторяют Φ и ΦLmod. С 1+h x j ®cos(ц^) sinc sinc q d ^ + где q = ζl /2, а G1,2(Φ̃(ξ), k, q) – поправки к (8). При k = 1 G1,2 =0; при k =0 ЗД-2 можно переделать в ЗД-1, сдвинув зубцы на полпериода. Точные функции G1,2 имеют громоздкий вид и мало информативны. Они хранят «память» о зубцах ЗД – зависят от l через q. Мы численно рассчитали при Ф = ФL, hе[0,1; 0,6], q ≤ 1 и всех k поправку от G1 в (30) и в поле на выходе ПФ. Вклад G1 в отличие квадратной скобки в (30) от 1 оказался малым по сравнению с первым слагаемым. Вклад от G2 был оценен подбором при Φ = ΦL хорошего приближения для G2 и явной зависимости второго слагаемого в (30) от параметров и аргументов 4cosZ1+8cosZ • —-— J G2 ■ cos (ц^) d Z« 3 sin q х Z 1 Z(31) (1 - к2)h [ Ас cos ц + As sin ц], где α = μh, Αc =– 1/(32/21+α3/70), Αs = α /(96/11+α3/35). Модуль (31) ≤ 0,23l(1– k2)h, учитывая (11), q ≤ 1 и затухающие колебания с амплитудой ≤ 0,7 в квадратной скобке (31) при всех μ и h. В поле U2 (u, v) (16) на выходе ПФ функция (31) дает добавку ΔUG2 AUg, « 8( , к )h J1(v,q,цо)J2(u,h,Цо), (32) 3n2 J1( v,q,Цо) = J 0 cosZ ( q | —— sin q sin21 2 I cos(Zv)d Z ® 11(ц, Z, d) = 4sinc ц^ sinc Z-111 +112, где d=D / a, 111(ц, Z, d) — интеграл по четырем вырезанным по углам квадратам D×D, I12(μ, ζ, d) – интеграл по четырем вставленным четвертям кругов. Расчеты показали, что разница (33) и (7) незначительна. б) Рис. 5. Функции Ĵ1 (v, q, μ0) / q3 (а) и Ĵ2 (u, h, μ0) (б) из (32). μ0 = 50 Вместо I23 в (6) будет теперь 123 (ц, Z, d) = 1231 (ц, Z, d) + 1232 (ц, Z, d), (34) где I231 – интегралы типа I23 в (6) по полоскам H×2(a – D) (вместо H×2a) (полагаем, ширина зубцов подогнана под 2(a – D)), а I232 – интегралы по зубцам в углах d+h 1232(ц,Z,d) = 4 J ^(P)^(ц,Z,d,P)dp, (35) d где Ψ(ρ) – аналог Φ(t) в (9) в углах ЗД: половина суммы всех зубцов в 1 /4 кольца на расстоянии ρ от центра кольца; оба pe[d, d+h] и T(p)e[nd/4,0] нормированы на a. Т.к. вид Ψ(ρ) мало влияет на I232, в основном использовалась линейная модель Ψ(ρ) Yl (p) = nd (d + h -p)/4h. Функция W (μ, ζ, d, ρ) в (35) – сумма интегралов по М0 угловым зубцам. При М0 =0 в углах зубцов нет и W =0. W и I232 в (35) растут с ростом d и заметно зависят от М0, влияя на отличие U1 в (6, 12) от суммы iU1(ц, Z, f, d)/ O = 11 -111 + 112 + I231 + I232 , (37) тем самым качественно влияя на профиль пучка U2 в (13). Подстановка (37) в (13) дает для U2 (u, v) при δ = 0 -U 2( u, v, f + fi) = Ud (u, v, f + fi) + A U, (38) где Ud – результат интегрирования в (13) без I232 (35) (т.е. при М0=0), а ΔU – вклад от I232 ∆U(u,v) =1 µ0cos(µu) dµζ0I232 ⋅cos(ζv)dζ. (39) π00 Срезы по v у (38, 39) в сравнении с U2 (16) рассчитывались для М0 =0÷5 при μ0∈[10; 40], d∈[0,1; 0,3] и h∈[0,2; 0,4]. Примеры приведены на рис. 6. Плато U2 мало зависят от вида Ψ(ρ) и Φ (t), поэтому в основном для них брались функции (36) и (21). Как видно, ΔU заметно проявляется в U2 на краю плато, где у U2 (16) для ЗД-1 имеется небольшой амплитудный нарост, роль которого не мала при круглых ЗД [14, 15]. В зависимости от μ0, h, d и М0 ΔU может уменьшить, увеличить или сдвинуть нарост, деформируя края плато. Вклад ΔU волнообразный по поперечной координате. При М0 =0 (нет зубцов в углах ЗД и ΔU = 0) у ЗД-3 вырез углов меньше, чем у ЗД-1, что тоже влияет на край плато, где с ростом d нарост может даже стать выемкой. При всех М0 все эффекты усиливаются с ростом d; роль μ0 и h слабее. Вклад ΔU в U2 обычно максимален при М0 = 1 и падает с ростом М0. б) а) Рис. 6. Срезы по v = 0 функций ΔU (u, v) (39) и – U2 (u, v, f+f1) (38) при ΨL (ρ) (36), Φ̃L (t) (21), h = 0,3, d = 0,1 Влияние зубцов в углах ЗД на пучок на выходе ПФ надо оценивать конкретно в каждом случае.
3. Разделение переменных у поля на выходе ПФ Для квадратных ЗД переменные пóля на выходе ПФ не разделяются, в отличие от входного поля. Оценим роль второго слагаемого в (16) у поля на выходе ПФ для ЗД-1 при δ =0 и зубцах вида (21). В приближении ГО поле (20) в углах крыльев пучка нулевое. Профили срезов по v совпадают при v ≤ 1 – единичное плато и крылья Φ(u), и прямоугольные с плато Φ(v) при v > 1. При конечном μ0 U2 в (16) – это промежуточное положение от произведения (19) к вырезу углов крыльев в (20). Типичные примеры срезов по v у U2 (16) при μ0∈[20, 60] и h∈[0,2; 0,4] показаны на рис. 7. Срезы нормированы на 1 в центре. При v< 1 (плато по v) все срезы от u почти сливаются и описываются (19). А на краю плато и на спаде по v это не так. Наибольшее отличие для абсолютных величин – при v ≈ 1 (край плато). При v ≥ 1 значения U2 (u =0) (на которые кривые нормированы на рис. 7) близки значениям (19) от v. На спаде (по крайней мере, до v ≤ 1+ h) относительные кривые сближаются, как на плато, иногда почти сливаются, но с более крутым спадом по u, чем в (19). Чем больше μ0, тем на меньшем интервале спада по v происходит переход от одного семейства близких по виду функций к другому. При μ0 ≤ 30 (рис. 7а) переход захватывает почти весь интервал v ≥ 1, а при μ0 ≥ 40 нормированные кривые, например, на рис. 7б слились уже при v ≥ 1,1. а) 0.4 0.6 0.8 1 1.2 1.4 И б) 0.4 0.6 0.8 1 1.2 1.4 И Рис. 7. Срезы по v нормированных кривых U2 (u, v, f+f1) (16) для ЗД-1 при δ = 0 и Φ̃ = Φ̃L
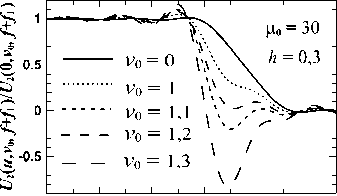
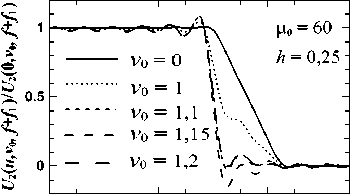
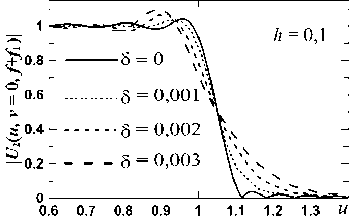
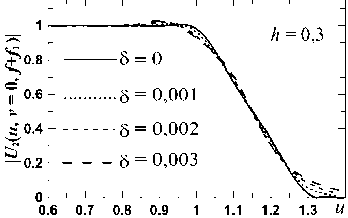
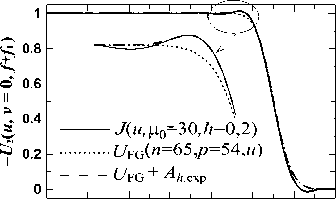
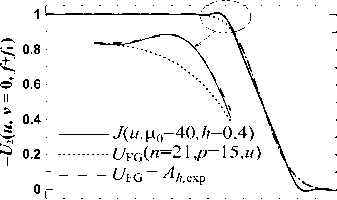
4. Приближение Френеля До сих пор мы пренебрегали фазовым параметром δ (15) и его влиянием на пучок U2 (13). Для данных [1] δ ≈ 0,002. В [7, 8] для круглой ЗД расчеты показали, что δ ≤ 0,005 мало влияет на амплитуду выходного пучка, и нулевой фронт на входе остается почти таким же на выходе. Для квадратной ЗД-1 мы рассчитали поправки за счет δ≤ 0,003 в (16) при h ≤ 0,5 и μ0 ≤ 60. При δ ≠ 0 у пучка на краю плато появляется фазовый нарост (до ≈ 10 ÷ 15% от π /2) и может измениться нарост амплитуды. Фазовый нарост растет с ростом μ0 и δ и уменьшением h. На плато фаза остается близкой нулю. Нарост амплитуды при δ ≠ 0 слабо увеличивается с ростом δ, сильно уменьшается с ростом h и почти не зависит от μ0 по величине. С ростом h и μ0 он сужается и сдвигается к краю плато. Расчеты показали, что эти изменения пучка почти не влияют на его искажение за ПФ и приближение δ =0 оправдано. На рис. 8 показаны примеры влияния δ на поперечный срез U2 (u, v) на плато (совпадающий с (18)). Из рис. 8 видно, что с ростом h уменьшаются и амплитудный нарост на плато, и его деформация, и увеличение наклона крыльев пучка (слабо зависящее от μ0) с ростом δ. Они мало заметны уже при h ≥ 0,2. а) б) Рис. 8. Зависимость |U2 (u, v = 0, f+f1)| (16) от δ при μ0 = 40, h = 0,1 (а) и h = 0,3 (б); Φ̃ = Φ̃L
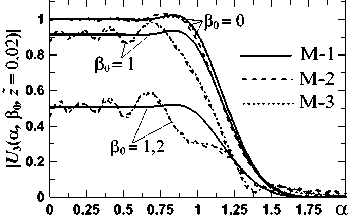
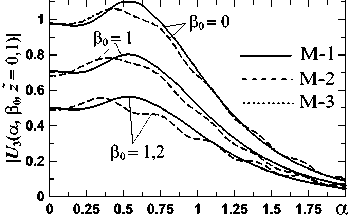
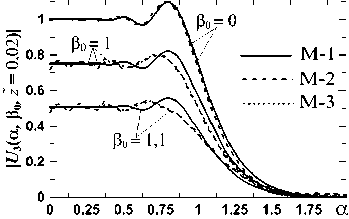
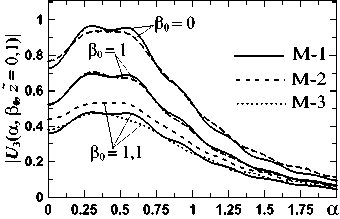
5. Распространение пучка за ПФ Как и для круглых ЗД в [14, 15], платообразные поперечные профили пучков U2 (u, v) (13) близки функциям сплюснутого Гаусса (flattened Gauss) [21], медленно искажающимся при распространении nk UFG(n, p,u) =e-pu2Pn(рu2) =e-pu2∑ u2k, (40) k=0 k! где Pn(рu2) – полином степени n из первых членов ряда Тейлора для exp (pu2). Это позволяет для расчета поля за ПФ моделировать поле на выходе ПФ из (40) с поправками. Сделаем это для ЗД-1 при Φ = ΦL и δ =0, поскольку в [14, 15] показано, что фазовый нарост у U2(u, v) при δ ≤ 0,003 дает малую поправку поля за ПФ. Мы сопоставили (40) с поперечными сечениями U2 на плато (в виде (19)). Были разобраны 3 примера подбора n и p в (40) под спад (19), определяемый в основном h: (n; p) = (65; 54) для (μ0; h) =(30; 0,2); (n; p) =(35; 27) для (μ0; h) =(20; 0,3) и (n; p) =(21; 15) для (μ0; h) = (40; 0,4). На рис. 9 показаны два из них. Заметим, что т.к. спад крыльев при квадратных ЗД близок Φ (u), а не Φ (u)/ u, как при круглых, то для равных μ0 и h спад в первом случае немного круче, т.е. n больше. Мы рассчитали поле за ПФ из ПУ-3 (рис. 1) без учета амплитудного нароста, определяемого как Ah = | J |– UFG, а потом оценили вклад Ah с помощью разных моделей поля U2 (u, v) и Ah. Из рис. 7 и (16) видно, что модель М-1 поля U2 (u, v) на выходе ПФ в виде UFG (n, p, u)×UFG (n, p, v) не учитывает уменьшения поля в углах на крыльях. Поэтому были взяты еще две модели: предельная М-2, в которой у крыльев поля М-1 полностью вырезаны углы, как в ГО (20); и промежуточная М-3 в виде UFG (u)×UFG (v)– I (u)×I (v) (как в (16)), где, согласно (19), I (u, μ0)= UFG (u)– [Si (μ0 (1 – u)) + Si (μ0(1+ u))] / π и для вычитаемого при u ≥ 0 и μ0 ≥ 30 использовано хорошее приближение из [22] в виде соединения 5 аналитических кусков. Срезы поля в углах М-3 оказались весьма близкими точным кривым типа на рис. 7. а) б) Рис. 9. Аппроксимация J (u, μ0, h) (19) при Φ = ΦL и δ = 0 как UFG (40) и UFG+Ah,exp. Для Ah,exp (42) в (а) b0 = 0,022; u0 = 0,96; k0 = 326,5; в (б) b0 = 0,037; u0 = 0,98; k0 = 285,71 В решении ПУ-3 U3(α, β, z̃)= Û(α, z̃)×Û(β, z̃) для поля М-1 переменные разделены, как в М-1, а Û (α, z̃) (одномерное решение ПУ для UFG; срез U3 по β) выражается аналитически через полиномы Эрмита [16, 18]. Это поле нормировано, как в (13), а из координат {x, y, z} за ПФ поперечные {x, y} – как {u, v} в (14): α = (af1 / f ) x, β = (af1 /f ) y, а z – на число Френеля за ПФ NF =(af1/ f )2/ λz z = Xz(f / af1)2/2п = 1/2nNF. (41) По данным [1], для z =50 м z̃ ≈ 0,02 (NF ≈ 8). В [14, 15] для круглых ЗД максимум был z̃ ≈ 0,1 (NF ≈ 1,6). В этом интервале и рассмотрим срезы U3 (α, β, z̃) по поперечной координате. Изменения Û (α, z̃) при разных (n, p) с ростом z̃ (41) качественно одинаковы и различаются количественно. Фаза (вначале нулевая) появляется и растет на краю плато и на спаде. Спад становится более пологим с почти локализованной при |Û | ≈ 0,5 точкой, и на краю плато растет выступ, сначала двигающийся к центру, а потом и ломающий плато на ряд провалов и выступов (сплошные линии на рис. 10). Сравнение срезов U3 (α, β, z̃) для М-1,2,3 показало, что при z̃ = 0,02 ÷ 0,1 отличия U3 (α, β, z̃) малы и на плато, и на крыльях. На рис. 10 это показано для двух вышеупомянутых примеров. Кривые для М-2 и М-3 почти везде неразличимы. Т.е. вид U2 (u, v, f +f1) в углах спадов от модели М-3 до нуля не сказывается на поле за ПФ. Вполне можно брать модель М-3 (даже М-1) для описания плато пучка за ПФ и влияния на него Ah. Для изучения влияния Ah мы добавили к (40) в моделях М-1,3 разные виды Ah, подобранные под разницу (40) и (19): Гауссоиду (рис. 9) и 2 модели с быстро и медленно затухающими колебаниями у Ah по обе стороны от основного максимума – в виде J0 и sinc Ah,exp(u ± u0) = bо exp[-kо (u ± uо)2 ],(42) Ah jo( u ± u о) = bо J [ kо( u ± u о)],(43) Ah,sinc(u ± uо) = bo sinc[kо(u ± uо)].(44) а) в) г) Рис. 10. Срезы |U3 (α, β = β0, z̃)| от α при разных β0 и моделях М-1,2,3 поля на выходе ПФ: (а),(б) – с Û (n = 21, p = 15) для (μ0; h) = (40; 0,4); (в),(г) – с Û(n = 65,p = 54) для (μ0; h) = (30; 0,2) Тогда для U2 (u, v, f +f1) в М-1,2,3 (40) меняется на UFG (n, p, u) +Ah (u – u0)+ Ah (u + u0). Для нароста Ah,exp интеграл в ПУ-3 рассчитывается аналитически [18]. Добавки Ah увеличивают отклонение фазы от нуля и искажения амплитуды на краю плато U3 (α, β, z̃). Мы рассчитали для трех вышеприведенных примеров в М-1,3 роль Ah на расстояниях z̃ =0,02÷0,1 при параметрах Ah, отвечающих реальным значениям и при b0 в (42-44) в 1,5 ^ 5 раз больше. Во всех случаях влияние Ah на U3(α, β, z̃) оказалось малым. Вид Ah (43, 44) с затухающими колебаниями по бокам основного экстремума позволяют оценить вклад наростов для ЗД-3, поскольку, как видно из поправок к амплитудам в этом случае, например, на рис. 6, амплитудный нарост может получить дополнительную колебательную структуру. Влияние таких Ah сильнее, чем (42), но все равно малó. Рассчитали мы вклад Ah вида (43, 44) и при b0 < 0, как это может быть с ЗД-3. Ah тогда уменьшает искажения в U3 (α, β, z̃), но тоже мало. В итоге оказалось, что наросты при квадратной ЗД меньше, чем при круглой с близкими значениями μ0 и h, и их влияние на пучок за ПФ слабее, даже если взять наросты близких размеров. Искажения пучка на рассмотренных z̃ определяются функцией (40), амплитудные экстремумы на плато лишь слегка увеличиваются при b0 > 0 или уменьшаются при b0 < 0, а фронт пучка остается близким к плоскому. Сами Ah и их вклад растут с ростом h (уменьшением n). Поэтому в отличие от случая круглой ЗД нет необходимости убирать амплитудный нарост: это мало изменит вид и глубину модуляции пучка на рассмотренных расстояниях. И вырезание зубцов в углах квадратной ЗД заметно не влияет на вид U3 (α, β, z̃). Заключение В продолжение работ [7, 8, 14, 15] для круглых ЗД путем последовательного решения трех ПУ рассчитано поле на выходе и за аподизатором, состоящим из квадратных ЗД и ПФ. Основное внимание уделено различию результатов для круглых и квадратных ЗД. Как и с круглой ЗД, с квадратной ЗД поле на выходе аподизатора при безразмерных параметрах: отношении высоты зубца ЗД к размеру ЗД hе[о,1; о,6], размеру ОД в фокусе ПФ рое[Ю;бо] и фазе, учитывающей дифракцию Френеля, δ ≤ 0,003, – близко платообразному пучку вида сплюснутого Гаусса [21], медленно искажающемуся при распространении. И отличается от него на краю плато небольшим амплитудным Ah и (при δ ≠ 0) фазовыми наростами. Различие здесь для круглых и квадратных ЗД в следующем: 1) При близких параметрах аподизаторов наросты с квадратной ЗД меньше и влияние их на искажение пучка за ПФ на расстояниях z =1/(2пNf)е[о,о2^о,1] (что отвечает числам Френеля за ПФ NF ≈ 8÷1,6) меньше даже при одинаковых размерах наростов. 2) Крылья пучка на выходе ПФ с круглой ЗД в приближении ГО выражаются через форму Φ(t) зубца ЗД функцией Φ (u)/ u, а с квадратной ЗД – Φ(u). Поэтому с квадратной ЗД при конечных μ0 спад крыла круче, менее плавен вблизи нуля и ближе форме зубца. 3) При круглых ЗД отношение ширины и высоты зубца ЗД H / L не определяет близость крыла пучка к форме зубца: внизу крыла знаменатель Φ (u) /u сглаживает Φ(u), а на переходе от плато к крылу сильно сказывается дифракция. При квадратных ЗД появляется параметр Р = μ0h. Граничное условие для близости формы крыла и Φ (u) – Р ≈ 8÷10. Вместе с ограничением на размер ОД у ПФ, требование Р > 12 трансформируется в H/L > 6, что совпадает с рекомендацией [1]. При выполнении обратного условия H/L ≤ 6 форма крыла пучка заметно отлична от Φ(u); нужного вида для нее можно добиться и с помощью простых, например, треугольных зубцов подбором его параметров. В круглых ЗД это возможно при всех H/L. 4) После обрезания ОД аподизатора поперечной структуры поля от круглых ЗД пучок обретает исходную радиальную симметрию. В квадратных ЗД это не так: из-за наличия у нее углов исходное поле в виде произведения одинаковых функций по поперечным осям приобретает в лучшем случае вид суммы таких произведений. От вида углов ЗД поле на выходе ПФ меняется как раз в области края плато, где находятся вышеупомянутые аплитудно-фазовые наросты, и на крыльях. Видом углов ЗД можно не только убрать амплитудный нарост (что в круглых ЗД требует дополнительных приспособлений), но даже получить вместо нароста выемку. Однако, т.к. при квадратных ЗД и наросты, и их роль в деформации пучков за ПФ слабее, чем при круглых, нет особого смысла подбирать специальные вырезы углов ЗД. Рассмотрев 3 варианта ЗД, с зубцами в углах и без них, мы показали, что и простой срез углов заметно не ухудшает качества выходного пучка и не сказывается на его деформации на расстояниях NF ≈ 8 ÷1,6 в числах Френеля.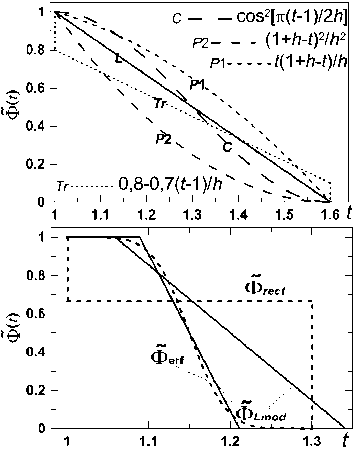
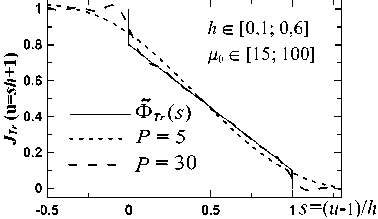
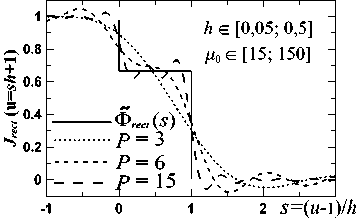
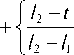
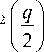
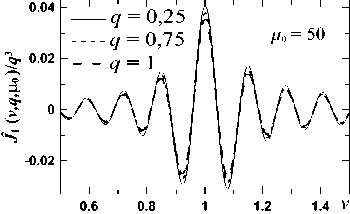
Список литературы Формирование пучков в аподизаторе с квадратной зубчатой диафрагмой
- Auerbach JM, Karpenko VP. Serrated-apertures apodizers for high-energy laser systems. Appl Opt 1994; 33(15): 3179-3183. DOI: 10.1364/AO.33.003179.
- Vinokurov GN, Gorbunov VA, Pavlov AV, Yashin VE, Serebryakov VA. Investigation of apodized apertures for elimination of self-focusing of smal scale perturbations in nonlinear media. In Book: Proc VIII USSR Conf on Coherence and Nonlinear Optics. Vol 2. Tbilisi: "Metsniereva" Publisher; 1976: 239.
- Alekseev VN, Jilin AN, Starikov AD, Chernov VN. Formation of a spatial profile of a beam in a laser amplifier by a system comprising a hard aperture and a spatial filter. Quantum Electron 1980; 10(9): 1186-1188. DOI: 10.1070/QE1980v010n09ABEH010738.
- Bel’kov SA, Voronich IN, Garanin SG, Zimalin BG, Rukavishnikov NN, Savkin AV, Sharov OA. Study of the apodization of a laser beam by serrated aperture stops for high-power installations of laser thermonuclear synthesis. J Opt Technol 2015; 82(6): 330-338. DOI: 10.1364/JOT.82.000330.
- Bel’kov SA, Voronich IN, Garanin SG, Zimalin BG. Toothed apodizing stops with high radiation strength. J Opt Technol 2016; 83(2): 113-118. DOI: 10.1364/JOT.83.000113.
- Epatko IV, Malutin AA, Serov RV, Solovyev DA, Chulkin AD. New algorithm for numerical simulation of the propagation of laser radiation. Quantum Electron 1998; 28(8): 697-702. DOI: 10.1070/QE1998v028n08ABEH001307.
- Sizova IM, Moskalev TYu, Mikheev LD. Laser beam shaping with circular serrated apertures. I. Spatial filtering. Appl Opt 2019; 58(18): 4905-4909. DOI: 10.1364/AO.58.004905.
- Sizova IM, Moskalev TYu, Mikheev LD. Laser beam shaping with circular serrated apertures. II. Theory of the beam profile formation. Appl Opt 2019; 58(18): 4910-4917. DOI: 10.1364/AO.58.004910.
- Aristov AI, Grudtsyn YaV, Zubarev IG, Ivanov NG, Konyashchenko AV, Krokhin ON, Losev VF, Mavritskiy AO, Mamaev SB, Mesyats GA, Mikheev LD, Panchenko YuN, Rastvortseva AA, Ratakhin NA, Sentis ML, Starodub AN, Tenyakov SYu, Utéza OP, Tcheremiskine VI, Yalovoi VI. Hybrid femtosecond laser system based on a photochemical XeF(C-A) amplifier with an aperture of 12 sm [In Russian]. Atmospheric and Oceanic Optics 2009; 22(11): 1029-1034.
- Mikheev LD, Tcheremiskine VI, Uteza OP, Sentis ML. Photochemical gas lasers and hybrid (solid/gas) blue-green femtosecond systems. Prog Quantum Electron 2012; 36: 98-142. DOI: 10.1016/j.pquantelec.2012.03.004
- Alekseev SB, Aristov AI, Grudtsyn YaV, Ivanov NG, Kovalchuk BM, Losev VF, Mamaev SB, Mesyats GA, Mikheev LD, Panchenko YuN, Polivin AV, Stepanov SG, Ratakhin NA, Yalovoi VI, Yastremskii AG. Visible-range hybrid femtosecond systems based on a XeF(C–A) amplifier: state of the art and prospects. Quantum Electron 2013; 43(3): 190-200. DOI: 10.1070/QE2013v043n03ABEH015096.
- Mikheev LD, Losev VF. Multiterawatt hybrid (solid/gas) femtosecond systems in the visible. In Book: Viskup R, ed. High energy and short pulse lasers. IntechOpen; 2016: 131-161. DOI: 10.5772/63972.
- Alekseev SB, Ivanov NG, Losev VF Mesyats GA, Mikheev LD, Ratakhin NA, Panchenko YuN. Attainment of a 40 TW peak output power with a visible-range hybrid femtosecond laser system. Quantum Electron 2019; 49(10): 901-904. DOI: 10.1070/QEL17050.
- Sizova IM, Moskalev TYu, Stavrovskii DB. Correction of shape distortions in laser beams apodized with circular serrated apertures. Appl Opt 2021; 60(16): 4861-4870. DOI: 10.1364/AO.423334.
- Sizova IM, Stavrovskii DB. Limits of the correction ring applicability in an apodizer with a circular serrated aperture. Computer Optics 2022; 46(3): 395-405. DOI: 10.18287/2412-6179-CO-1079.
- Vinogradova MB, Rudenko OV, Sukhorukov AP. Wave theory [In Russian]. Moscow: "Nauka" Publisher; 1979. ISBN: 978-5-9710-1558-1.
- Van Wonterghem BM, Speck DR, Norman MJ, Wilcox RB, Karpenko VP, Richards JB. Compact and versatile pulse generation and shaping subsystem for high-energy laser systems. Proc SPIE 1993; 1870: 64. DOI: 10.1117/12.154490.
- Prudnikov AP, Brychkov YA, Marichev OI. Integrals and series. Volume 1: Elementary Functions. New York: Gordon and Breach; 1998. ISBN: 978-2-88124-089-2.
- Korn M, Korn GA. Mathematical handbook: For scientists and engineers. New York: McGraw-Hill Book Company; 1968. ISBN: 978-5-458-25439-7.
- Willis HF. LV. A formula for expanding an integral as a series. Philosophical Magazine 1946; 39: 455-459. DOI: 10.1080/14786444808521694.
- Gori F. Flattened Gaussian beams. Opt Comm 1994; 107: 335-341. DOI: 10.1016/0003-4018(94)90342-5.
- Abramowitz M, Stegun IA, eds. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. New York: Dover Publications; 1965. ISBN: 978-0-486-61272-0.


