Формирование радиально-поляризованных пучков Бесселя нулевого порядка методами дифракционной и поляризационной оптики
Автор: Карпеев Сергей Владимирович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Короткое сообщение
Статья в выпуске: 4 т.40, 2016 года.
Бесплатный доступ
Предложена оптическая система для генерации азимутально- и радиально-поляризованных лазерных пучков Бесселя нулевого порядка. Формирование пучка Бесселя нулевого порядка осуществляется амплитудным дифракционным аксиконом, а преобразование поляризации основано на интерференции в многослойной структуре. Экспериментально получен радиально-поляризованный пучок Бесселя нулевого порядка с использованием бинарного амплитудного аксикона.
Амплитудный дифракционный аксикон, бесселевы пучки, радиальная поляризация, интерференционный поляризатор
Короткий адрес: https://sciup.org/14059499
IDR: 14059499 | DOI: 10.18287/2412-6179-2016-40-4-583-587
Текст научной статьи Формирование радиально-поляризованных пучков Бесселя нулевого порядка методами дифракционной и поляризационной оптики
Азимутально- и радиально-поляризованные лазерные пучки на сегодняшний день имеют множество приложений [1], в частности, для оптической манипуляции [2]. Методы формирования цилиндрических векторных пучков различаются как по параметрам сформированных пучков, так и по свойствам формирующих систем. Одновременно с поляризационным состоянием формируется и амплитудно-фазовое распределение пучка, которое также играет важную роль. Например, радиально-поляризованные моды высоких порядков позволяют получить более острую фокусировку [3, 4] и тем самым добиться сверхразрешения. Для оптического захвата и манипуляции требуются либо модовые пучки сложной формы [5], либо вихревые пучки высоких порядков [6, 7]. Таким образом, с практической точки зрения было бы интересно формирование требуемых поляризационных состояний при заданном амплитудно-фазовом распределении пучка.
Универсальным средством решения этой задачи представляются жидкокристаллические модуляторы света [8], однако разрешение и энергетическая эффективность этих устройств всё ещё недостаточны для решения определённого круга задач.
Когерентная суперпозиция пары обычных мод Гаусса–Эрмита [9, 10] даёт радиально- либо азимутально-поляризованное распределение, амплитуда которого соответствует кольцевой моде R-TEM (0,1) . Другой вариант метода, основанный на суперпозиции вихревых пучков, даёт возможность управлять распределением комплексной амплитуды с помощью ДОЭ [11]. Основным недостатком интерферометров, используемых для сложения мод, является низкая стабильность, а основным достоинством – высокое качество формирования пучков.
Секторные пластинки [12, 13] позволяют преобразовывать поляризационное состояние пучков с произвольным осесимметричным распределением ампли- туды, характеризуются высокой энергетической эффективностью (теоретически 100 %) и стабильностью. Однако качество формируемых пучков сильно зависит от качества изготовления пластинок, которые, по сути, всегда дискретны. В большинстве случаев такие пучки требуют дополнительной фильтрации, что снижает эффективность формирования и искажает распределение амплитуды.
Применение анизотропных материалов [14, 15] также даёт возможность управлять амплитудным распределением, если исходные пучки с вихревой фазой формируются при помощи ДОЭ [15]. Энергия исходного пучка делится между одновременно получаемыми пучками с радиальной и азимутальной поляризациями. Разделение этих двух пучков при помощи фильтрации, как и в случае секторных пластинок, может приводить к искажениям амплитудного распределения.
Поляризационное преобразование, происходящее при падении пучков на поверхность диэлектрика под углом Брюстера [16– 18], также может применяться для генерации неоднородных поляризаций. Такие системы могут быть как внутри- [16, 17], так и внерезона-торными [18] и основаны на использовании конических волновых фронтов, сформированных соответствующими оптическими элементами. Наибольшей эффективностью обладают внутрирезонаторные системы, поскольку обеспечивают многократное прохождение Брюстеровских окон или призм. Брюстеровские окна [16], обеспечивающие радиальную либо азимутальную поляризацию, представляют сложности в изготовлении. Более простой является система Брюстеровских призм [17], состоящая из двух аксиконов. Для повышения коэффициента отражения азимутальной поляризации в [17] применялось многослойное диэлектрическое покрытие конической поверхности призмы Брюстера. Такая система производит только радиально-поляризованное распределение с амплитудой, соответствующей кольцевой моде R-TEM (0,1) .
Генерация цилиндрических векторных пучков с необходимым амплитудным распределением может осуществляться внерезонаторными системами с падением света под углом Брюстера, включающими ДОЭ, например [18]. Для увеличения степени поляризации прошедшего излучения в системе [18] использовалась стопа Столетова. Однако диаметр пучка после прохождения стопы Столетова сильно увеличился из-за большого значения угла Брюстера. Демонстрация радиальной поляризации осуществлялась по изображению на матовом экране, а коллимация пучка не осуществлялась. В работе [19] был предложен и теоретически обоснован метод уменьшения угла расходимости поляризованного излучения путём замены стопы Столетова на интерференционный поляризатор, имеющий меньшие рабочие углы.
В данной работе предложена оптическая система для генерации пучка Бесселя нулевого порядка, поляризованного либо азимутально, либо радиально. Система включает амплитудный бинарный аксикон для генерации пучка Бесселя и интерференционный поляризатор, дающий возможность генерации как азимутальной, так и радиальной поляризаций.
Экспериментальное исследование
Пропускание многослойного интерференционного поляризующего покрытия отличается для p - и s -поляризаций излучения при ненулевых углах падения. Можно рассчитать толщины слоёв так, что для заданной длины волны λ0 при одном угле падения будет наблюдаться максимальное пропускание для p -поляризации и минимальное для s -поляризации, а при другом – наоборот. Интерференционный поляризатор состоял из 20 чередующихся слоев Ta2O5/SiO2 различной толщины, нанесённых на кварцевую подложку диаметром 12,7 мм и толщиной 5 мм. Поляризационные характеристики пропускания изготовленного поляризатора исследовались на спектральном эллипсометре J.A. Wollam V-VASE в диапазоне углов 0–45° с шагом 0,2°. Длина волны зондирующего излучения устанавливалась равной 632,8 нм, ширина спектра – не более 1,2 нм. Для большей точности перед каждым измерением определялся уровень излучения спектрального блока эллипсометра (базовая линия), а результаты измерений усреднялись во времени по 10 точкам. Зависимости пропускания p - и s -поляризованного излучения от угла падения приведены на рис. 1. Из измеренных характеристик следует, что интерференционный поляризатор обеспечивает отношение коэффициентов пропускания азимутальной и радиальной компонент Ts / Tp около 100:1 – 140:1 для углов падения 27-30°. При этом пропускание для Ts около 70%.
Расчёт показывает, что для получения таких углов дифракции кольцевая решётка аксикона должна иметь период 1,3– 1,4 мкм. Для создания пучка Бесселя нулевого порядка в работе использовался амплитудный дифракционный аксикон с периодом 1,4 мкм и диаметром 10 мм, изготовленный на круговом лазерном записывающем устройстве CLWS-200S мето- дом термохимического окисления маски хрома. Электронная фотография аксикона приведена на рис. 2.
Пучок, прошедший через интерференционный поляризатор, имеет меньшую расходимость, чем в работе [18] из-за значений рабочих углов меньших, чем угол Брюстера. Для получения изображения на ПЗС-камере в этом случае можно использовать изображающий высокоапертурный объектив 60×, который строит изображение на поверхности фотодетектора.
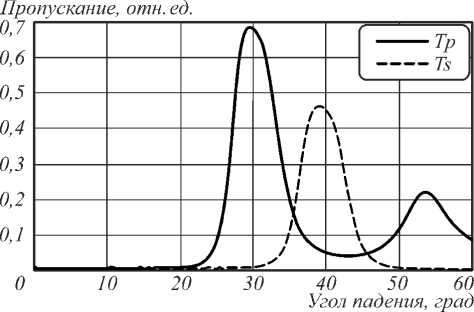
Рис. 1. Зависимости пропускания p- и s-поляризованного излучения от угла падения

Рис. 2.Электронная фотография фрагмента дифракционного аксикона
Исследование формирования азимутально-поляризованного излучения на основе интерференционного поляризатора осуществлялось на оптической установке (рис. 3). Она включала: линейно-поляризованный гелий-неоновый лазер ЛГН-208А, пространственный фильтр – расширитель пучка, четвертьволновую пластину (WP), дифракционный аксикон (DA), интерференционный поляризатор (IP), изображающий высокоапертурный объектив 60×, плёночный поляризатор (P), видеокамеру DCM310 (CCD).

Рис. 3. Схема экспериментальной установки для получения радиально-поляризованного пучка Бесселя нулевого порядка
На рис. 4 приведены полученные распределения интенсивности для различных положений оси поляризатора.
Из рис. 4 видно, что полученный пучок Бесселя нулевого порядка имеет радиальную поляризацию.

Рис. 4. Пучок Бесселя при различных положениях поляризатора: 0° (а), 45° (б), 90° (в), без поляризатора (г)

Заключение
Таким образом, предложена оптическая система для эффективного формирования радиально-поляризованного пучка Бесселя нулевого порядка, включающая бинарно-фазовый аксикон и интерференционный поляризатор. Система основана на преобразовании конического волнового фронта при прохождении через многослойную структуру. Формирование пучка Бесселя нулевого порядка с коническим волновым фронтом осуществлялось бинарным амплитудным дифракционным аксиконом, а изображение полученного неоднородно поляризованного пучка строилось при помощи высокоапертурного микрообъектива. Радиально-поляризованный пучок Бесселя нулевого порядка может применяться для оптической манипуляции.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, а также гранта РФФИ 14-02-97033р_поволжье_а.
Список литературы Формирование радиально-поляризованных пучков Бесселя нулевого порядка методами дифракционной и поляризационной оптики
- Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications/Q. Zhan//Advances in Optics and Photonics. -2009. -Vol. 1, Issue 1. -P. 1-57. - DOI: 10.1364/AOP.1.000001
- Shvedov, V. A long-range polarization-controlled optical tractor beam/V. Shvedov, A.R. Davoyan, C. Hnatovsky, N. Engheta, W. Krolikowski//Nature Photonics. -2014. -Vol. 8. -P. 846-850. - DOI: 10.1038/nphoton.2014.242
- Khonina, S.N. Experimental demonstration of the generation of the longitudinal E-field component on the optical axis with high-numerical-aperture binary axicons illuminated by linearly and circularly polarized beams/S.N. Khonina, S.V. Karpeev, S.V. Alferov, D.A. Savelyev, J. Laukkanen, J. Turunen//Journal of Optics. -2013. -Vol. 15(8). -085704 (9pp). -DOI: 10.1088/2040-8978/15/8/085704.
- Khonina, S.N. Strengthening the longitudinal component of the sharply focused electric field by means of higher-order laser beams/S.N. Khonina, S.V. Alferov, S.V. Karpeev//Optics Letters. -2013. -Vol. 38, Issue 17. -P. 3223-3226. - DOI: 10.1364/OL.38.003223
- Порфирьев, А.П. Оптический захват и перемещение микрочастиц с помощью асимметричных пучков Бесселя-Гаусса/А.П. Порфирьев, А.А. Ковалёв, В.В. Котляр//Компьютерная оптика. -2016. -Т. 40, № 2. -С. 152-157. - DOI: 10.18287/2412-6179-2016-40-2-152-157
- Морозов, А.А. Сложные вихревые пучки для вращения микромеханических элементов/А.А. Морозов, Р.В. Скиданов//Компьютерная оптика. -2013. -Т. 37, № 1. -С. 68-75.
- Rykov, М.A. Modifying the laser beam intensity distribution for obtaining improved strength characteristics of an optical trap/М.A. Rykov, R.V. Skidanov//Applied Optics. -2014. -Vol. 53(2). -P. 156-164. - DOI: 10.1364/AO.53.000156
- Čančula, M. Generation of vector beams with liquid crystal disclination lines/Miha Čančula, Miha Ravnik, Slobodan Žumer//Physical Review E. -2014. -Vol. 90. -022503. - DOI: 10.1103/PhysRevE.90.022503
- Khonina, S.N. Generating inhomogeneously polarized higher-order laser beams by use of DOEs beams/S.N. Khonina, S.V. Karpeev//Journal of the Optical Society of America A. -2011. -Vol. 28, Issue 10. -P. 2115-2123. - DOI: 10.1364/JOSAA.28.002115
- Khonina, S.N. Grating-based optical scheme for the universal generation of inhomogeneously polarized laser beams/S.N. Khonina, S.V. Karpeev//Applied Optics. -2010. -Vol. 49, Issue 10. -P. 1734-1738. - DOI: 10.1364/AO.49.001734
- Khonina, S.N. Polarization converter for higher-order laser beams using a single binary diffractive optical element as beam splitter/S.N. Khonina, S.V. Karpeev, S.V. Alferov//Optics Letters. -2012. -Vol. 37(12). -P. 2385-2387. - DOI: 10.1364/OL.37.002385
- Алфёров, С.В. Экспериментальное исследование фокусировки неоднородно поляризованных пучков, сформированных при помощи секторных пластинок/С.В. Алфёров, С.В. Карпеев, С.Н. Хонина, О.Ю. Моисеев//Компьютерная оптика. -2014. -Т. 38, № 1. -С. 57-64.
- Kawauchi, H. Simultaneous generation of helical beams with linear and radial polarization by use of a segmented half-wave plate/H. Kawauchi, Y. Kozawa, S. Sato, T. Sato, S. Kawakami//Optics Letters. -2008. -Vol. 33(4). -P. 399-401. - DOI: 10.1364/OL.33.000399
- Machavariani, G. Birefringence-induced bifocusing for selection of radially or azimuthally polarized laser modes/G. Machavariani, Y. Lumer, I. Moshe, A. Meir, S. Jackel, N. Davidson//Applied Optics. -2007. -Vol. 46. -P. 3304-3310. - DOI: 10.1364/AO.46.003304
- Khonina, S.N. Generation of cylindrical vector beams of high orders using uniaxial crystals/S.N. Khonina, S.V. Karpeev, S.V. Alferov, V.A. Soifer//Journal of Optics. -2015. -Vol. 17, Issue 6. -065001 (11p). -DOI: 10.1088/2040-8978/17/6/065001.
- Tovar, A.A. Production and propagation of cylindrically polarized Laguerre-Gaussian laser beams/A.A. Tovar//Journal of the Optical Society of America A. -1998. -Vol. 15, Issue 10. -P. 2705-2711. - DOI: 10.1364/JOSAA.15.002705
- Kozawa, Y. Generation of a radially polarized laser beam by use of a conical Brewster prism/Y. Kozawa, S. Sato//Optics Letters. -2005. -Vol. 30, Issue 22. -P. 3063-3065. - DOI: 10.1364/OL.30.003063
- Скиданов, Р.В. Дифракционные аксиконы для формирования радиально-поляризованного света на основе использования стопы Столетова/Р.В. Скиданов, А.В. Морозов//Компьютерная оптика. -2014. -Т. 38, № 4. -С. 614-618.
- Паранин, В.Д. Расчёт формирования радиально-поляризованных пучков на основе рефракционных элементов с интерференционными поляризующими покрытиями/В.Д. Паранин, С.В. Карпеев, С.Н. Хонина//Компьютерная оптика. -2015. -Т. 39, № 4. -С. 492-499. - References DOI: 10.18287/0134-2452-2015-39-4-492-499


