Формирование сечений телекоммуникационных сетей для анализа их устойчивости с различными мерами связности

1. Введение. Проблема анализа устойчивости является довольно востребованной как в области телекоммуникаций [1-6], так и в других отраслях, занимающихся разработкой и эксплуатацией сложно разветвленных сетей [7-9].

В современных телекоммуникационных сетях на первый план выходят услуги типа виртуальных частных сетей, для которых организуются многоточечные соединения, не укладывающиеся в понятие двухполюсной связности. В качестве типового примера можно рассмотреть магистрального оператора Ростелеком (рис. 1), которому обычно требуется предоставить услугу виртуальной сети для распределенного географически потребителя, что подразумевает его подключения сразу в нескольких вершинах графа (обычно более, чем в двух, например, в вершинах 2, 26 и 45). Тогда для оператора оказывается востребованной задача расчета надежности сети, в которой адресатами будут выступать данные вершины. В результате классический подход к анализу двухполюсной связности оказывается отчасти несостоятельным при подобной трактовке проблемы, поскольку потребует анализа сразу нескольких вероятностей (между 2 и 26, 2 и 45, 26 и 45 вершинами), каждая из которых будет характеризовать устойчивость лишь в конкретном направлении. В этой связи в работе предлагается расширить подобный подход для анализа многополюсной и всеполюсной связностей.

Рис. 1. Граф – модель магистральной сети Ростелеком

С точки зрения теоретических предпосылок существующий математический аппарат анализа надежности сетей достаточно хорошо описывает методы непосредственного расчета вероятности связности сети на основе сформированного множества типовых подграфов сети. Здесь можно упомянуть такие методы, как прямой перебор состояний элементов системы связи, прямой перебор состояний связности и несвязности системы связи, приведение к простейшим структурам, оценка на основе метода декомпозиции (теоремы разложения Шеннона–Мура), оценка на основе преобразований булевой алгебры (логико-вероятност-

_{_______}DIGITAL INFORMATIO_{_}N TELECO_{_}MM_{_}UNICATION TECHNOLOGIES_{_______} ный метод), объединение связных подграфов или сечений с поглощением, метод двудольных графов. Однако проблеме синтеза множеств типовых состояний (путей, деревьев, сечений) посвящено не так много работ. Кроме того, обычно рассматриваются алгоритмы формирования сечений и анализируется их вычислительная сложность, глубоко не вдаваясь в подробности их математического описания, что требует определенной интуиции при разработке и отладке программ. В этой связи в настоящей работе сделана попытка математической формализации алгоритмов формирования множеств сечения для различных мер связности при условии их некоторой модификации с целью снижения вычислительной сложности.

Наиболее подходящей моделью сети для подобного рода задач оказывается модель, использующая постулаты теории графов [10]. При этом предположение о случайном характере отказов отдельных звеньев телекоммуникационной сети позволяет ее рассматривать в виде обобщенной модели Эрдеша–Реньи [11]. В ней рассматривается случайный граф G , в котором жестко задано множество вершин V = { 1, _ , v } с мощностью v . Естественно, что случайными в нем являются только ребра, что вполне согласуется с предположением об абсолютной устойчивости сетевых устройств. В классическом подходе анализируются исключительно графы, в которых отсутствуют кратные ребра (мультиграфы), петли (псевдографы) и направленные ребра (орграфы). Всего потенциальных ребер в графе G l = С П штук. Вероятность существования ребра (работоспособности линии связи) между вершинами i и j обозначена через p i j е [ 0,1 ] и не зависит от всех остальных l - 1 ребер. Отметим, что данная вероятность может рассматриваться и как коэффициент готовности и коэффициент оперативной готовности [3], и как другие показатели, характеризующие работоспособность элементов телекоммуникационной сети [4]. Предполагая, что L – случайное множество ребер, существующее после реализации отдельного опыта, случайный граф G приобретает форму обобщенной модели Эрдеша–Реньи, т. е. G = ( V , L ) . Заметим, что вероятность p_G существования конкретного графа G в результате опыта есть:

pg = П p-j П (1- pj.

( - , j ) е L      ( i , j ) < L

Хорошо известно, что вероятность выхода из строя элементов может трактоваться в форме коэффициента готовности и коэффициента

_{_}ЦИ_{_}ФРОВЫЕ ИНФОРМАЦ_{_}ИОННО-ТЕЛЕКОМ_{_}МУНИКАЦИОННЫЕ ТЕХНОЛОГИИ_{_} оперативной готовности [12], а также в виде других показателей, характеризующих работоспособность элементов телекоммуникационной сети [13]. В результате вероятность p ( 5 ) обладания случайным графом G некоторым свойством трактуется как сумма вероятностей p_G существования графов, принадлежащих множеству S , для которого этого свойство выполняется, то есть

Р (5 ) = ЕPg .

G e S

При анализе устойчивости телекоммуникационной сети под рассматриваемым свойством обычно понимают связность сети. Следовательно, вероятность p ( 5 ) связности сети оценивается как сумма вероятностей существования p_G всех связных графов (на заданном множестве вершин), формирующих множество S .

Основываясь на представлении о понятии стохастической связности сети как соответствии некоторого случайного графа свойству связности между заданным набором вершин, традиционно выделяют три меры связности: двухполюсная, многополюсная и всеполюсная [10, 14]. Для всех данных мер множество S графов, для которого выполняется свойство связности, имеет следующий вид:

5 = { G: 3 Sic G}.

То есть множество S состоит из всех графов G , для которых существует хотя бы один подграф S_i , содержащийся в графе G .

Следует отметить, что процедуры определения множества S графов, для которого выполняется свойство связности, оказываются весьма нетривиальными задачами, иногда даже более трудоемкими, чем последующее вычисление вероятности связности. Кроме того, фактически случайный граф в данном контексте распадается на совокупность детерминированных составляющих, определяющих данное множество S . В настоящей работе предлагаются алгоритмы, позволяющие для произвольного графа телекоммуникационной сети и трех типов связности формировать подобное множество S , элементами которого являются соответствующие сечения. В последующем на их основе оказывается возможным рассчитывать вероятность связности сети.

• 2.    Формирование множества минимальных двухполюсных сечений. Сам по себе термин сечение, или разрез, обозначает набор

ребер, удаление которых приводит к нарушению связности исходного графа [10, 15]. Отметим, что здесь под связностью в общем случае понимается многополюсная связность, а в частных – двухполюсная и всеполюсная [16, 17]. Минимальное же сечение является, по сути, тем же самым сечением, но включение (работоспособность) любого из его ребер приводит к связности исходного графа. Таким образом, минимальное сечение – это набор ребер, только полное удаление которых приводит к нарушению связности исходного графа. Отметим, что в литературе, посвященной анализу надежности сложных систем, обычно слово "минимальное" опускают, считая это самим собой разумеющимся. Здесь и далее, если нет неоднозначности в толковании понятия минимальное сечение, также будем использовать термин сечение. Отдельно следует остановиться на термине вершинное сечение, являющимся минимальным сечением, приводящим к изоляции данной вершины от всех остальных элементов графа.

Рассматриваемый подход базируется на методе, использующем в качестве основы матрицу связностей, и предполагающем последовательный перебор всех сочетаний вершинных сечений, начиная с истока и стока [10, 18]. Отметим, что данный способ приводит к включению в общий состав сечений не минимальных, что потребовало введения дополнительной процедуры проверки добавляемого сечения на безызбыточность.

Формально процедуру формирования множества минимальных двухполюсных сечений целесообразно разбить на три этапа. На первом синтезируют v -1 множество вершинных сечений, выделяя в отдельный блок сечение истока и стока. На втором находят декартово произведение сечений, не являющихся истоком и стоком, вплоть до v - 3 по- лученного множества с учетом неповторяемости ребер, отсутствия ребер, принадлежащих истоку, и невключенности всех ребер сечения стока в получаемое множество. На заключительном третьем вычисляют декартово произведение полученных на втором этапе произведений на вершинное сечение истока, контролируя уникальность ребер.

Исходными стей A = 3

I ¹, ^jM , j = 1, v

данными является матрица смежно случайного графа G, на основе которой с исполь- зованием соотношений:

f j

' '     IEav, a,j = 1, aVj = aj ,1 = 1 Г =1

[0, a,- j = 0, j = 1,..., v,

Г i - 1 V            j

‘     ‘ IZE+ E air, a.,j= 1, ai, j = a J , i = 5 k =1 r = k        r=k

[c, ai,j = 0, i = 2, ..., v,j = 1, ..., v, достаточно легко вычисляется модифицированная матрица смежностей A '. Заданное направление связи образуется двумя вершинами: истоком с номером vs и стоком с номером vt.

Процесс формирования множества вершинных сечений разбивается на два этапа. Так, необходимо образовать две матрицы, одна из которых включает только сечения истока и стока, а вторая – все остальные. Таким образом, целесообразно первоначально образовать двухэлементный вектор, содержащий номера полюсных вершин (истока и стока):

k =

s

vt

Тогда вектор, содержащий номера оставшихся неполюсных вершин включает v - 2 элемента:

k ‘ = { { i } : i t k , i = 1, ..., v } .

Следовательно и матрица полюсных вершинных сечений

C ' = { c ,j } i = 1, . i , ^и неполюсных C = { c i , j } i = 1,..., i аналогичны по струк- j = 1,2                                              j = 1, v - 2

туре. Данные матрицы также формируются путем последовательной процедуры сравнения элементов модифицированной матрицы A ' смежностей с индексами образуемых матриц C или C сечений:

'

'

, i = 1, . , l ,      (1)

^a k , r ^{: a} k , r = i , k = 1, •., ^v , r =

C • = ci, j

'

j,j < min (v, v), ak, j = i, k = 1, .., v, r = 5 j -1, min (v,, vt )< j < max (v,, vt), ^, j - 2,j > max (v, v),

i = 1, . , l, j = 1, ..., v - 2.

Формирование декартовых произведений неполюсных сечений в случае матричного представления сечений несколько упрощается и формализуется в алгебраическом виде. Так, на первом шаге образуются вектора w _k , являющиеся, по сути, векторами неполюсных вершинных сечений, обязательно содержащие ребра сечения истока и невключающие все ребра сечения стока:

w k = { C :max ( C¹ + C ' ¹ ) = 2, min ( C¹ - C ' ² ) * 0, i = 1, . , v - 2 } .     (2)

Проверка тождества max ( C + C ¹ ) = 2 эквивалентна нию неуникальных ребер сечения истока C ^'1 в неполюсном C ¹ , неравенства min ( C¹ - C ² ) ^ 0 - присутствия в сечении

выявле-

сечении

C ⁱ всех

ребер сечения стока C ^'2.

На последующих шагах образуются вектора w _k , являющиеся декартовыми произведениями до порядка v - 3 неполюсных вершинных сечений C ⁱ . При этом дополнительно к контролю содержания ребер сечения истока и невключенности всех ребер сечения стока удаляются повторяющиеся ребра:

wk

= <  c ' : c ' = 1 ₁

- sign ( с - 1 1 ) О sign ( с - 1 1 ) ,

v-2 v-2 v-2 r c = Z Z . Z ZC1J, j^ v - 2,

i '1 =1 1 2 = 1 1 +1      1 r = 1 r - 1 +1 j =1

max (c + C1) = 2, min (c - C2) ^ 0, r = 2, ., v - 3 >, где x' = {Xj} = sign (x) = jxj- - вектор, полученный из исходного вектора x x = {Xj}, каждый элемент которого:

xi

xi xi ,

О - произведение Адамара [19].

Здесь вычисление вектора с' = 1 l - sign (c -1 l) О sign (с -1 l) экви- валентно удалению повторяющихся ребер из декартового произведения сечений, представленного в форме суммы всех возможных перестано- вок векторов сечений c =z z -

v -2 r

Z z c i j .

i '1 =1 i 2 = i 1 +1 i r = i r — 1 +1 j =1

Заключительный шаг состоит в вычислении декартового произведения полученных векторов w _k на вектор сечения истока C ^'1 с одновременным удалением неуникальных ребер и проверкой добавляемого сечения на безызбыточность и добавлении сечений истока и стока:

W = C ',

Wk+2 = lw :w = 1, -(w, + C'1 -1,)o(w, + C'1 -1Д lk l k l min(Wi - w) * 0, min(w - Wi) * 0,i = 1,-, k -1},          (5)

k = 1, ...,rows ( w ) .

Здесь проверка тождественности неравенства min ( W i - w ) * 0

эквивалентна выявлению факта принадлежности множества ребер добавляемого сечения w множеству ребер уже добавленного сечения

W i ,

а неравенства min ( w - W i ) * 0 - наоборот.

• 3.    Формирование множества минимальных всеполюсных сечений. Рассматриваемый подход базируется на методе, использующем в качестве основы матрицу связностей, предполагающем последовательный перебор всех сочетаний вершинных сечений, не включая одну из вершин, считаемую терминальной [10, 20, 21]. В отличие от процедур, используемых в данном методе, выполняющих проверки на инцидентность соседних вершинных сечений, а также на связность графа, полученного после

удаления заданной комбинации вершинных сечений, более простым решением оказался контроль добавляемого сечения на уникальность.

Формально процедуру формирования множества минимальных всеполюсных сечений целесообразно разбить на три этапа. На первом синтезируют v множеств вершинных сечений. На втором анализируют на уникальность полученные вершинные сечения и формируют исходное множество сочетаний вершинных сечений, состоящее из v - 1 множеств вершинных сечений, обычно удаляя из рассмотрения сечение первой вершины. На третьем образуют все сочетания отобранных v - 1 множеств вершинных сечений, последовательно сохраняя только уникальные сочетания сечений.

Исходными данными является матрица смежностей a=aai l 1' ГЦ, j=1, ■

случайного графа G ,

на основе которой вычисляется модифицированная матрица смежностей A'.

В рамках данного подхода множество вершинных сечений целесообразно представлять в виде вектора–строки номеров вершинных се- чений C1 = cT ={£,'},=

., v -1

состоящего из номеров вершин, образую- щих множество анализируемых сечений. Поскольку удобно не рассматривать сечение именно первой вершины, то:

C , = i + 1, 1 = 1,..., v - 1.

Первое уникальное всеполюсное сечение графа – это сечение этой первой вершины, т. е. первый столбец матрицы W всепо-люсных сечений формируется путем анализа первого столбца матрицы A смежностей:

W 1 = { a j ,1 : a j ,1 = i , j = 1, . , v } , i = 1, . , l .                   (7)

Оставшиеся v - 1 вершинных сечений образуют столбцы матрицы W всеполюсных сечений только в случае их уникальности. Для этого первоначально для каждого k -го сечения вычисляется вспомогательный вектор w = { w , } 1 l , являющийся вектором, идентифицирующем это вершинное сечение:

Wi = { a j , k : a j , k = z , j = 1,..., v } , z = 1, _ , l , k = 2,..., v ,               (8)

который и проверяется на неповторяемость:

W k = { w : min ( w - W¹ ) * 0, i = 1, ,..,k - 1 } .                (9)

Далее на каждом шаге образуются сочетания вершинных сечений в форме матриц C r сочетаний порядка r , r = 1, ,.. , v - 1. При этомразре-шенные комбинации не включают в себя потенциально не образующие минимальные сечения. Так для каждой вершины есть предел перебора номеров вершин, определяемый номером максимальной инцидентной вершины и задаваемый в виде вектора c = { c i } , = 1 - 1 , каждый элемент которого рассчитывается на основе матрицы A смежностей:

c , = { max ( j ) : a , + 1, j = 1, j = 1, .„, v } , i = 1, .„, v - 1.              (10)

В результате матрицы C _r сочетаний формируются на основе последовательного перебора сначала по номерам i столбцов предыдущих матриц, а затем по номерам j всех допустимых вершинных сечений:

^k C _r

- r - 1

' c j

: i = ^.„cols ( C r - 1 ) , [ C r - 1 ] r - 1

I r -1

>.

J r - 1 J

Также на каждом шаге проверяется уникальность добавляемого сечения. Для этого для каждого k -го сочетания вычисляется вспомогательный вектор w = { w i } , = 1 l , являющийся вектором, идентифицирующем это сочетание:

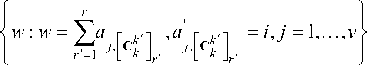
i = 1,,.., l , k = 2,,.., v ,

Далее из него удаляются повторяющиеся ребра:

w' = 1 l - sign ( 1 l - w ) О sign ( 1 l - w )

и выполняется проверка на неповторяемость:

W k = { w ' :min ( w ' - W ' ) ^ 0, i = 1,..., k - 1 } .              (14)

• 4.    Формирование множества минимальных многополюсных сечений. Рассматриваемый подход аналогичен использованному при формировании множества минимальных всеполюсных сечений и отличается лишь процедурой отбора используемых для образования матрицы сечений комбинаций. При этом из всего множества сечений сохраняются лишь содержащие полюсные вершины.

Исходными данными является также матрица смежностей A = { a ' , j } ' . = 1 случайного графа G .

В рамках данного подхода также рассчитывается вектор– строка номеров вершинных сечений C1 = c 'T = {c', } на ос-

нове соотношения (6).

Далее образуют вектор, содержащий номера вершин, не являющихся полюсами. Так, если номера вершин–полюсов v образуют век- тор k = {k'} .=1 v‘, то вектор k' = {k'}

’ - v '

k' = {{'}: ' ^ k, ' = 1, ..., v} включает номера только неполюсных вершин.

Первый столбец матрицы W всеполюсных сечений формируется путем анализа не только первого столбца матрицы A смежностей, но и в том случае, если первая вершина является полюсом:

w^ = { a . ,1 ^:1' ^G k , a j■ ,1 = ' , j = 1, • • •, v } , ' = 1,• • •, ¹ . (15)

Оставшиеся v - 1 вершинных сечений образуют столбцы матрицы W всеполюсных сечений только в случае их уникальности и принадлежности к множеству полюсов. Для этого аналогично формуле (8) первоначально для каждого k -го сечения вычисляется вспомогательный вектор w = { W ' } ' = 1 _l , идентифицирующий это вершинное сечение:

w, = { aj , k : i e k , a^k = i , j = 1, _ , v j , i = 1,.. . , l , k = 2, ,..,v ,

который и проверяется на неповторяемость в соответствии с равенством (9).

Процедуры (10)–(11) выполняются идентично и в результате формируются матрицы C _r сочетаний.

При расчете вспомогательного вектора w = { w J^j l дополнительно к выражению (12) необходимо проверять на принадлежность используемых вершин к множеству полюсов:

r i = 1,..., l, k = 2,^, v,

Удаление повторяющихся ребер и проверка на уникальность производятся по тем же соотношениям (13)-(14). В результате данных процедур формируется матрица многополюсных сечений W .

• 5.    Реализация предложенных процедур на примере простейшей сети. Рассмотрим реализацию предложенных процедур на примере формирования минимальных двухполюсных сечений. Структура сети представлена на рисунке 2. Источник и сток на рисунке также отмечены квадратами: v , = 1, v_t = 5. Таким образом, вектор полюсов k равен:

  k

  
  

Рис. 2. Двухполюсный граф исследуемой сети связи

Вектор неполюсных вершин равен:

	" 2 " 3
к ‘ =
	4
	_ 6 .

Матрица смежностей графа данной задается формулой:

"0 1 0 0 0 0" 1 0 1 0 0 1 0 1 0 1 0 1 A = 0 0 1 0 1 0 ,                           (18) 0 0 0 1 0 1 _0 1 1 0 1 0. а модифицированная матрица – выражением:

	" 0	1	0	0	0	0 "
	1	0	2	0	0	3
	0	2	0	4	0	5
A ' =	0	0	4	0	6	0	.                           (19)
	0	0	0	6	0	7
	_ 0	3	5	0	7	0 .

В соответствии с процедурой (1) рассматривается матрица полюсных вершинных сечений размером 7 х 2 :

"1 0" 0 0 0 0 с = 0 0 0 0 0 1 L0 1. и матрица неполюсных вершинных сечений размером 7 х 4 :

	10 0 0 110 0 10 0 1
C =	0 110 0 10 1 0 0 10 . 0 0 0 1 _

Согласно выражениям (2)-(3) порядок вычисляемых декартовых произведений равен трем:

	1		1		1		1		1		1
	1		0		1		1		0		0
	1		1		1		0		1		0
w 1 =	0	, w 2 =	1	, w 3 =	1	, w 4 =	0	, w 5 =	0	, w 6 =	1
	0		1		0		1		1		0
	0		0		1		0		1		0
	0		0		0		1		0		1

Отметим, что из всех исходных столбцов матрицы C сохраняется только первый {1} – w ₁ , поскольку все оставшиеся ({2}, {3}, {4}) не включают ни одного ребра сечения истока. Комбинации пар также остаются только те, в которых фигурирует первый столбец матрицы C , т. е. {1, 2} – w ₂ , {1, 3} – w ₃ и {1, 4} – w ₄ . Аналогично сохраняются оставшиеся комбинации из трех столбцов, включающие только первый столбец, за исключением комбинации {1, 3, 4}, которая полностью включает сечение сток, т. е. {1, 2, 3} – w ₅ , {1, 2, 4} – w ₆ .

Итоговая матрица двухполюсных сечений формируется в соответствии с соотношениями (4)-(5) и имеет размер 7 х 7 :

	1	0	0	0	0	0	0
	0	0	1	0	1	0	0
	0	0	1	1	0	1	0
W =	0	0	0	1	0	0	1
	0	0	0	1	1	1	0
	0	1	0	0	0	1	0
	_ 0	1	0	0	1	0	1

Отметим, что только вектор w ₃ оказывается избыточным, поскольку содержится в сечении W ³ ( w ₁ ). Все остальные сечения образуют столбцы матрицы W из векторов w _k путем обнуления элемента первой строки, идентифицирующего единственное ребро сечения истока W ¹ .

Множество двухполюсных сечений изображено на рисунке 3.

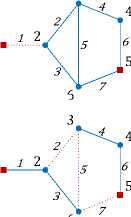
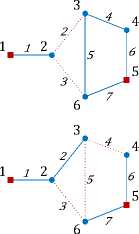
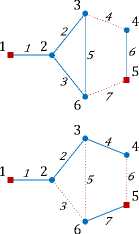
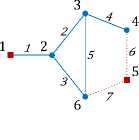
Рис. 3. Двухполюсные сечения в направлении 1-5 графа, представленного на рисунке 2

Далее рассмотрим реализацию предложенных процедур на примере формирования минимальных всеполюсных сечений. Структура сети представлена на рисунке 4. Матрица смежностей графа данной задается формулой (18), а модифицированная матрица – выражением (19). Вектор-строка вершинных сечений согласно выражению (6) имеет вид:

C 1 = c ' T = [ 23456 ] .

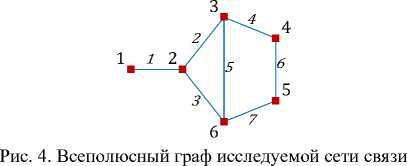
Первое уникальное всеполюсное сечение графа в соответствии с формулой (7) формирует исходную матрицу всеполюсных сечений, пока состоящую только из одного столбца:

W =

о

Далее в этому столбце добавляются только четыре из оставшихся пяти вершинных сечений, вычисляемых на основе соотношений (8)-(9), поскольку сечение второй вершины оказывается не минимальным и поглощается сечением первой вершины:

	1 0 0 0 0 0 10 0 0 0 0 0 0 1
W =	0 110 0 0 10 0 1 0 0 110 0 0 0 1 1

Вектор c пределов перебора рассчитывается с использованием выражения (10):

c =

Матриц C _r сочетаний согласно процедуре (11) образуется всего пять, причем первая из них C ₁ определена ранее как вектор-строка вершинных сечений:

C 2 =

^С з = 33

4 5

C 4 =

C

Отметим, что здесь перебор вариантов для четвертой вершины всегда заканчивается только четвертой, что существенно сокращает количество перебираемых комбинаций.

Далее в соответствии с выражениями (12)-(14) образуются оставшиеся столбцы матрицы всеполюсных сечений:

	" 1	0	0	0	0	0	0	0	0	0	0
	0	1	0	0	0	1	0	0	1	0	1
	0	0	0	0	1	0	0	1	0	1	1
W =	0	1	1	0	0	0	1	0	0	1	0
	0	1	0	0	1	1	0	1	1	1	0
	0	0	1	1	0	1	0	1	0	0	0
	0	0	0	1	1	0	1	0	1	0	0

Таким образом, W ¹ получено из первого вершинного сечения, т. е. из {1}, W ² – {3} ( C 1 ² ), W ³ – {4} ( C 1 ³), W ⁴ – {5} ( C 1 ⁴ ), W ⁵ –{6} ( C ₁⁵ ), остальные столбцы рассчитаны из комбинаций: W ⁶ из третьего и четвертого, т. е. {3, 4} ( C ⁵₂), W ⁷ – {4, 5} ( C ⁸₂), W ⁸ – {5, 6} ( C ⁹₂), W ⁹ – {3, 4, 5} ( C 3 ⁶), W ¹⁰ – {4, 5, 6} ( C ⁸ 3 ), W ¹¹ – {3, 4, 5, 6} ( C ⁴ 4 ). Отметим, что ни одна из комбинаций, содержащая сечение второй вершины, не порождает минимальное сечение, поскольку данное сечение включает в себя сечение первой вершины.

Множество всеполюсных сечений изображено на рисунке 5.

Наконец, рассмотрим реализацию предложенных процедур на примере формирования минимальных многополюсных сечений. Структура сети представлена на рисунке 6. Полюсами данного графа являются первая, четвертая и пятая вершины. Таким обра- зом, вектор полюсов:

k =

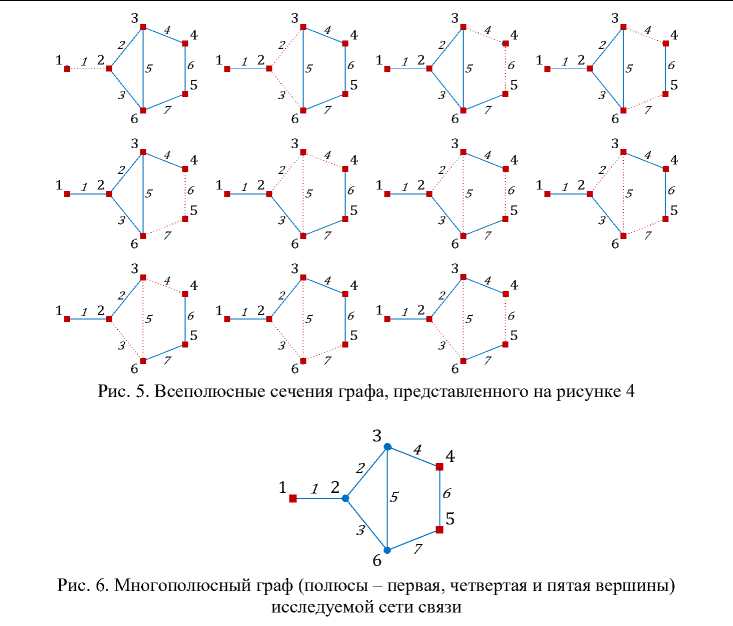
Матрица смежностей графа данной задается формулой (18), а модифицированная матрица – выражением (19). Вектор-строка вершинных сечений согласно выражению (6) имеет вид:

C 1 = c 'T = [ 23456 ] .

Первое уникальное многополюсное сечение графа в соответствии с формулой (15) формирует исходную матрицу многополюсных сечений, поскольку первая вершина является полюсом по условию:

W =

Далее к этому столбцу добавляются только две из оставшихся пяти вершинных сечений, вычисляемых на основе соотношений (16) и (9), поскольку вторая, третья и шестая вершины не являются полюсами:

	n 0 0 1 0 0 0 0 0 0
W =	0 1 0 0 0 0 0 1 1 _ 0 0 1 _

Вектор c пределов перебора рассчитывается аналогично с использованием выражения (10):

c =

Матриц C _r сочетаний согласно процедуре (11) также образуется всего пять:

C 2 =

	" 2	2	2	2	2	3	3	4
C 3 =	3	3	3	4	5	4	5	5
	_ 4	5	6	5	6	5	6	6

C 4 =

C 5 =

Далее в соответствии с выражениями (17), (13)-(14) образуются оставшиеся столбцы матрицы всеполюсных сечений:

	" 1	0	0	0	0	0	0	0	0
	0	0	0	1	0	0	1	0	1
	0	0	0	0	0	1	0	1	1
W =	0	1	0	0	1	0	0	1	0
	0	0	0	1	0	1	1	1	0
	0	1	1	1	0	1	0	0	0
	0	0	1	0	1	0	1	0	0

Таким образом, W ¹ получено из первого вершинного сечения, т. е. из {1}, W ² – {4} ( C ₁³ ), W ³ – {5} ( C ₁⁴ ), остальные столбцы рассчитаны из комбинаций: W ⁴ из третьего и четвертого, т. е. {3, 4} ( C ⁵₂), W ⁵ – {4, 5} ( C ⁸ 2 ), W ⁶ – {5, 6} ( C ⁹ 2 ), W ⁷ – {3, 4, 5} ( C ⁶ 3 ), W ⁸ – {4, 5, 6} ( C ⁸₃ ), W ⁹ – {3, 4, 5, 6} ( C ⁴₄ ). Отметим, что также ни одна из комбинаций, содержащая сечение второй вершины, не порождает минимальное сечение, а кроме того, вершинные сечения третьей и шестой вершины не порождают многополюсное сечение.

Множество многополюсных сечений изображено на рисунке 7.

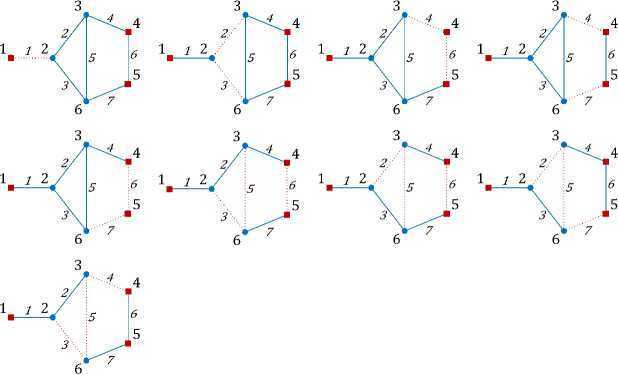
Рис. 7. Многополюсные сечения графа (полюсы – первая, четвертая и пятая вершины), представленного на рисунке 6

• 6.    Пример формирования множества сечений для магистральной сети Ростелеком. В качестве тестовой сети связи используется магистральная сеть Ростелеком, развернутая с целью формирования потоков в направлении "Европа – Азия" [16, 17]. Помеченный граф рассматриваемой сети связи представлен на рисунке 1.

Для двухполюсной связности оказывается возможным провести анализ для магистральной сети (рис. 1) целиком даже на основе сечений. На рисунке 8 представлены результаты формирования множества сечений для всех пар узлов, образующих направления связи. Здесь и далее на рисунках показаны все полученные величины в ходе расчетов, конкретные диапазоны изменения величин по оси абсцисс для каждого из рисунков детализируются в пояснениях. Нумерация n сечений задана сначала по номеру стока j при фиксированном истоке i , а затем и по номеру истока i , то есть номер сечения вычисляется по формуле:

, _x i ( i + 1 )

v - 1, j = i + 1, i + 2,..., v .

n = j + v ( i - 1 ) -    2^, i = 1,2,.

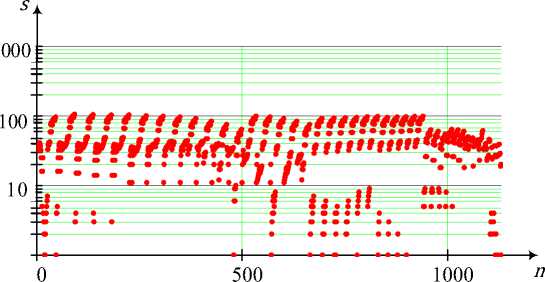
Рис. 8. Зависимость числа s сформированных сечений между заданными парами вершин от порядкового номера n сечения

Отметим, что максимальное количество сечений равно 105 в направлении связи 2 – 48 ( n = 92).

Оценка вычислительной сложности подобного рода алгоритмов является весьма неоднозначной задачей, вследствие зависимости числа выполняемых циклов от разветвленности графа. В связи с этим в настоящей работе приводятся оценки вычислительной сложности алгоритмов на основе анализа временных затрат на работу алгоритма для графа магистральной сети Ростелеком (рис. 1). Здесь и далее используется программная реализация алгоритмов в пакете MathCad, а расчеты проводятся в операционной системе Windows 8.1 на базе аппаратного обеспечения Intel® Core(TM) i5–3570 CPU @ 3.40GHz 3.80 GHz с оперативной памятью 4 Гбайт.

Временные затраты на формирование сечений представлены на рисунке 9. Стоит отметить, что здесь также время выполнения подобных вычислений не слишком велико и не превысило десяти секунд (максимальное значение характерно для наиболее богатых сечениями направлений связи) и составляет 8,238 с. Тем не менее, несмотря на почти в четыре раза меньшее число сечений, чем путей, максимальное время расчетов возросло более, чем на порядок, что связано, прежде всего, с более затратной процедурой перебора вершинных сечений.

Анализ временных затрат с точки зрения их зависимости от числа формируемых сечений (рис. 10) также показал наличие устойчивого тренда – с ростом количества сечений увеличиваются и требования к временным ресурсам. На рисунке отчетливо прослеживается тенденция возрастания не только минимального времени выполнения процедуры

_{_}ЦИ_{_}ФРОВЫЕ ИНФОРМАЦ_{_}ИОННО-ТЕЛЕКОМ_{_}МУНИКАЦИОННЫЕ ТЕХНОЛОГИИ_{_} для заданного числа формируемых подграфов при увеличении их количества, но и максимального времени для значительного числа сечений. Данное обстоятельство также связано с громоздкостью процедуры перебора вершинных сечений. Аналогично процедуре формирования путей, для незначительных по числу сечений направлений связи существуют отдельные выбросы, характеризующиеся значительным временем выполнения, определяемые как особенностями самого графа, так и порядком нумерации вершин [22–24].

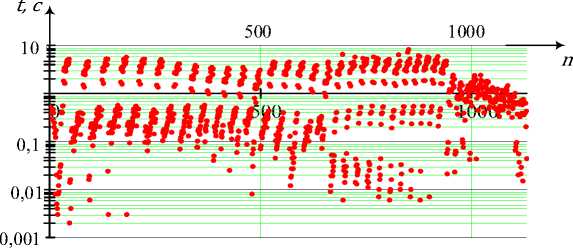
Рис. 9. Зависимость времени t выполнения процедуры формирования путей от их порядкового номера n

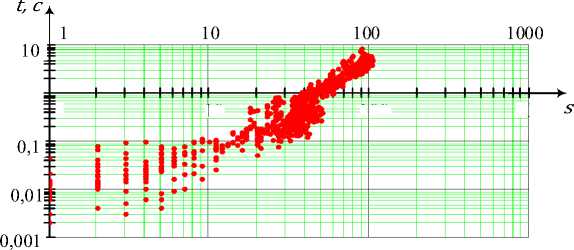
Рис. 10. Зависимость времени t выполнения процедуры формирования сечений от их количества s

Проведенный сравнительный анализ временных затрат формирования сечений показал существенные преимущества предложенного способа, поскольку для исследуемой сети выполнить расчеты оказалось невозможным на имеющихся вычислительных средствах с

_{_______}DIGITAL INFORMATIO_{_}N TELECO_{_}MM_{_}UNICATION TECHNOLOGIES_{_______} помощью известного подхода на основе матрицы смежностей [10, 18]. В результате для его реализуемости потребовалось разбивать граф (рисунок 7) на совокупность разрозненных подграфов, имеющих одинаковые точки сочленения. Только в этом случае оказалось возможным формировать сечения для каждого из подграфов в отдельности. На рисунке 11 показана зависимость выигрыша Δ t по времени, определяемая как разность между временем формирования сечений предложенным способом t r и методом поиска на основе матрицы связностей t t (cut sets enumeration using connection matrix), изложенным в [18], на основе выражения

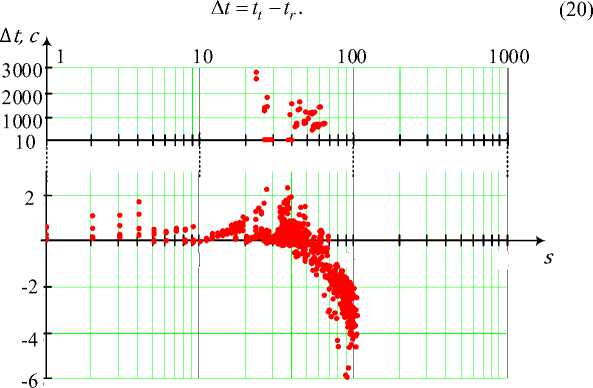
Рис. 11. Зависимость выигрыша Δ t по времени выполнения процедуры формирования сечений от их количества s

Отсюда наглядно подтверждаются существенные преимущества предложенного способа, поскольку лишь для значительного количества сечений наблюдается проигрыш по времени вычислений, что объясняется использованием дополнительных процедур разбиения графа на составляющие. Кроме того, для ряда наборов сечений характерны выигрыши, достигающие величин в несколько тысяч секунд. В данных случаях задействованные ресурсы практически приближаются к имеющимся в распоряжении.

В данном случае формирование сечений для всего графа (рис. 7) оказалось возможным только на основе предложенного способа. Для более подробного анализа рассматриваются также и усеченные случаи, когда исследуется подграф с заданным количеством ребер. На рисунке 12 представлены результаты формирования сечений. Исследования проводились для подграфов, составленных из первых n ребер до 57го включительно (n = 1,2,.,57 ), а также для подграфов, включающих только последние фиксированные ребра от 57-го до первого (n = 58,59,...,114). Отметим, что при n = 57,114 получаются идентичные исходные графы. Кроме того, для ряда подграфов (n = 64,65,86,87, ..,102 ) число сечений оказалось равным нулю, что свидетельствует о несвязности данных подграфов.

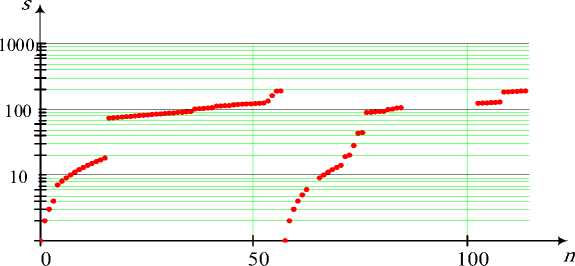
Рис. 12. Зависимость числа s сформированных всеполюсных сечений от порядкового номера n подграфа

Отметим, что максимальное количество всеполюсных сечений равно 190 для исходного графа магистральной сети ( n = 57,114).

Временные затраты на формирование всеполюсных сечений представлены на рисунке 13. Отсюда видно, что в зависимости от степени разветвленности графа (количества ребер) время выполнения операций варьируется в широких пределах – от близкого к нулю при числе сечений порядка единиц до величины в несколько минут (216 секунд) при максимальном числе сечений равным 190.

Анализ временных затрат с точки зрения их зависимости от числа формируемых всеполюсных сечений (рис. 14) показывает наличие устойчивого тренда – с ростом количества сечений увеличиваются и требования к временным ресурсам. Аналогично процедуре формирования двухполюсных сечений здесь прослеживается тенденция возрастания не только минимального времени выполнения процедуры для заданного числа формируемых подграфов при увеличении их количества, но и максимального времени для значительного числа сечений. Данное

_{_______}DIGITAL INFORMATIO_{_}N TELECO_{_}MM_{_}UNICATION TECHNOLOGIES_{_______} обстоятельство также связано, прежде всего, с громоздкостью процедуры перебора вершинных сечений. Следует также отметить наличие отдельных выбросов, характеризующихся сравнительно меньшими временами выполнения, определяемыми особенностями самого графа, а не его разветвленностью [25–27].

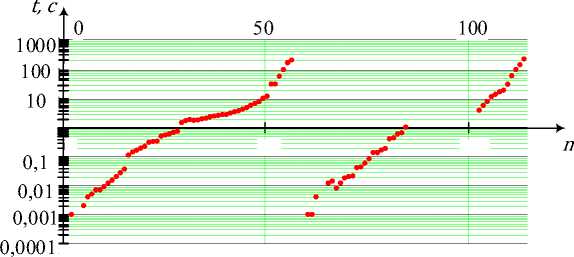
Рис. 13. Зависимость времени t выполнения процедуры формирования всеполюсных сечений от порядкового номера n подграфа

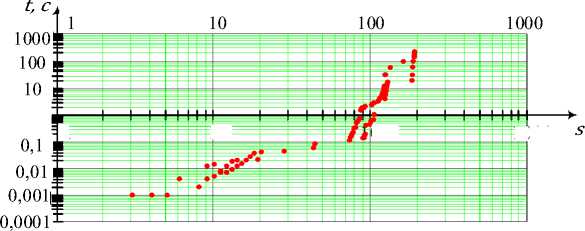
Рис. 14. Зависимость времени t выполнения процедуры формирования всеполюсных сечений от их количества s

Проведенный сравнительный анализ временных затрат формирования всеполюсных сечений показал преимущества предложенного способа для графов с числом сечений деревьев более ста. В качестве известного метода использован метод, генерирующий комбинации вершинных сечений из наборов меньшего порядка (generation of node set combination from its lower order node-sets [10, 20, 21]). На рисунке 15 показана зависимость выигрыша Δ t по времени, определяемая как разность между временем форми-

_{_}ЦИ_{_}ФРОВЫЕ ИНФОРМАЦ_{_}ИОННО-ТЕЛЕКОМ_{_}МУНИКАЦИОННЫЕ ТЕХНОЛОГИИ_{_} рования всеполюсных сечений предложенным способом t r и методом поиска, генерирующим комбинации вершинных сечений на основе наборов меньших порядков t t , на основе выражения (20).

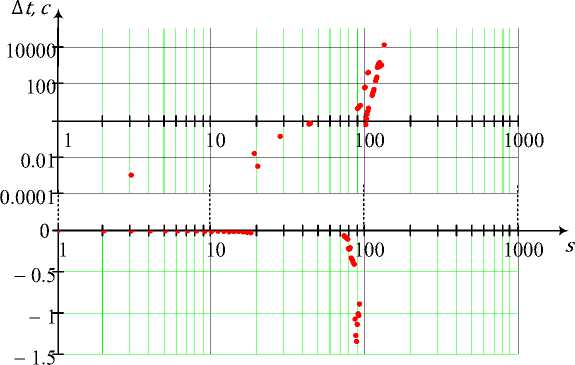
Рис. 15. Зависимость выигрыша Δ t по времени выполнения процедуры формирования всеполюсных сечений от их количества s

Отсюда следует, что для не слишком разветвленных графов, содержащих не более ста сечений, предложенный способ несколько проигрывает по времени вычислений (менее полутора секунд), вследствие необходимости проведения дополнительной процедуры проверки сечений на уникальность. В то же время за счет снижения избыточности неминимальных сечений для подграфов с числом сечений более ста выигрыш по времени оказывается весьма существенным (до нескольких десятков тысяч секунд). Кроме того, для подграфов с количеством всепо-люсных сечений более 133 ( n = 55,56,57,109,110,… ,114) вычисления на основе известного метода привели к превышению допустимого времени выполнения (более суток), в то время как предложенный способ успешно справился с задачей за приемлемое время, не превышающее четырех минут (рисунки 12-14).

В данном случае исследование всего исходного графа магистральной сети (рис. 1) оказалось доступным. На рисунке 16 представлены результаты формирования многополюсных сечений. Количество полюсов варьировалось от минимально допустимого числа, равного

_{_______}DIGITAL INFORMATIO_{_}N TELECO_{_}MM_{_}UNICATION TECHNOLOGIES_{_______} двум, и соответствующего случаю анализа направления связи до максимального, не эквивалентного остовому дереву, то есть 18. Для каждого фиксированного количества полюсов десять раз случайно выбрасывался набор вершин. Таким образом, всего рассмотрено 170 вариантов подграфов ( n = 1,2,...,170).

s

100          150 n

Рис. 16. Зависимость числа s сформированных многополюсных сечений от порядкового номера n подграфа

Отметим, что максимальное количество остовых деревьев сечений 164 для 17-ти полюсного подграфа ( n = 159). Однако результаты показывают, что количество сечений хотя и растет при увеличении номера рассматриваемого подграфа, но не столь стремительно, как для случая многополюсных деревьев.

Временные затраты на формирование многополюсных сечений представлены на рисунке 17. Видно, что время на выполнение данной процедуры проявляет тенденцию, отмеченную для количества сечений, – хотя временные затраты и возрастают, но рост оказывается незначительным. Данное обстоятельство является следствием необходимости проведения для всех типов подграфов процедуры отбора используемых для образования матрицы сечений комбинаций, вычислительные затраты на которую существенно снизить за счет уменьшения количества сечений практически не представляется возможным [28]. Отметим также, что временные затраты близки по абсолютным значениям к величине времени выполнения процедуры формирования всеполюсных сечений (рис. 12, 13).

Анализ временных затрат с точки зрения их зависимости от числа формируемых многополюсных сечений (рис. 18) показывает наличие устойчивого тренда – с ростом количества деревьев увеличиваются и

_{_}ЦИ_{_}ФРОВЫЕ ИНФОРМАЦ_{_}ИОННО-ТЕЛЕКОМ_{_}МУНИКАЦИОННЫЕ ТЕХНОЛОГИИ_{_} требования к временным ресурсам. Однако, очевидно, что относительный временной проигрыш оказывается весьма незначительным по причинам, описанным выше.

Время выполнения процедур формирования многополюсных сечений весьма слабо зависит от количества полюсов в исходном графе (рис. 19). Увеличение полюсности графа очень незначительно влияет на количество проверяемых комбинаций, что и приво-

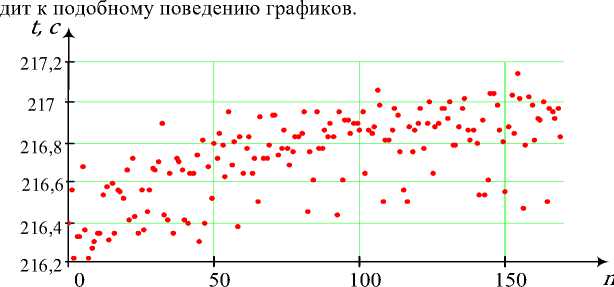
Рис. 17. Зависимость времени t выполнения процедуры формирования многополюсных сечений от порядкового номера n подграфа

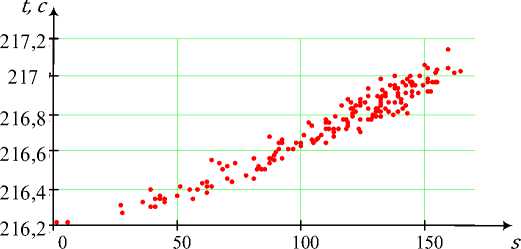
Рис. 18. Зависимость времени t выполнения процедуры формирования многополюсных сечений от их количества s

Подчеркнем, что приведенный подход аналогичен процедуре формирования всеполюсных сечений, с той лишь разницей, что для образования матрицы сечений комбинаций из всего множества сохраняются лишь те, которые содержат полюсные вершины [29–31]. По-

_{_______}DIGITAL INFORMATIO_{_}N TELECO_{_}MM_{_}UNICATION TECHNOLOGIES_{_______} скольку для известного метода, генерирующего комбинации вершинных сечений из наборов меньшего порядка (generation of node set combination from its lower order node sets [10, 20, 21]), получить результаты для графа магистральной сети (рис. 7) оказалось невозможным, то можно констатировать существенные преимущества предложенного метода с точки зрения вычислительных затрат.

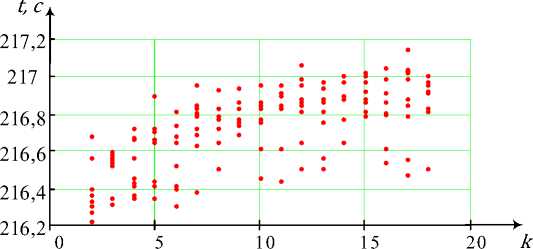
Рис. 19. Зависимость времени t выполнения процедуры формирования многополюсных сечений от количества их полюсов k

• 7.    Заключение. Следует отметить, что многополюсные сечения являются наиболее общим понятием относительно двухполюсных и всеполюсных [32, 33]. Несмотря на возможность подобного обобщения, в практических приложениях целесообразно рассматривать именно частные случаи вследствие их меньшей вычислительной сложности [3436].

Наиболее часто используемые методы анализа и синтеза сетей связи подразумевают рассмотрение вероятностного показателя устойчивости – вероятности связности. Основной упор при этом делается на исследовании влияния показателей надежности линий связи на устойчивость сети в целом. При этом в качестве технических параметров выступают коэффициент готовности для оценки надежности и коэффициент оперативной готовности для живучести. Значения этих двух параметров регламентируются действующим в настоящее время ГОСТ [12] и определяются характеристиками используемых систем передачи, среды распространения и категорией (приоритетом) пользователей. В результате при соответствующей замене вероятности связности на коэффициенты готовности или оперативной готовности оказывается воз-

_{_}ЦИ_{_}ФРОВЫЕ ИНФОРМАЦ_{_}ИОННО-ТЕЛЕКОМ_{_}МУНИКАЦИОННЫЕ ТЕХНОЛОГИИ_{_} можным применять существующие методы анализа вероятности связности для оценки устойчивости (надежности и живучести) реальных телекоммуникационных сетей, исходными данными для работы которых (методов) будут являться способы формирования сечений, предложенные в настоящей работе.