Формирование селеноцентрической орбиты космическим аппаратом с малой тягой

При осуществлении транспортных операций в системе Земля-Луна наиболее ответственным и сложным этапом перелета является этап формирования селеноцентрической орбиты. В данной статье предлагается подход к выбору управления с обратной связью позволяющий формировать управление на основе простых, известных законов управления. Предложенный закон управления обеспечивает формирование околокруго-вой селеноцентрической орбиты при достаточно широком изменении фазовых координат с учетом возмущений от гравитации Земли и Солнца.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ

Движение КА в системе Земля-Луна будем разделять на три участка. Этот подход описан в статье [1].

Геоцентрический перелет орбита выведения – промежуточная орбита. На этом участке учитываются возмущения от нецентральности гравитации Земли, атмосферы, притяжения Луны и Солнца. Управление рассчитывается по простым аналитическим зависимостям, полученным для центрального поля притяжения, и обеспечивает требуемый пространственный маневр.

Достижение сферы действия Луны. На этом участке определяется оптимальное управление в рамках круговой ограниченной задачи трех тел. Граничные условия перелета определяются параметрами промежуточной орбиты и целью миссии. Учитываются возмущения от притяжения Солнца, не учитываются от нецентральности гравитационного поля Луны (рис. 1).

После достижения сферы действия Луны фазовые координаты космического аппарата пересчитываются в селеноцентрическую систему координат (ССК). Центр ССК совпадает с центром Луны, главная плоскость ССК совпадает со средней плоскостью движения Луны. Ось Х направлена к точке весеннего равноденствия. В этом случае пересчет фазовых координат осуществляется по формулам (рис. 1):

r2 = 7rM2 -2rirM cos(A№)+ r2 , sin(a,2 )= rLSinf^^L)

r2        , cos(A^ 2 )= ricosW-rM r2            ,

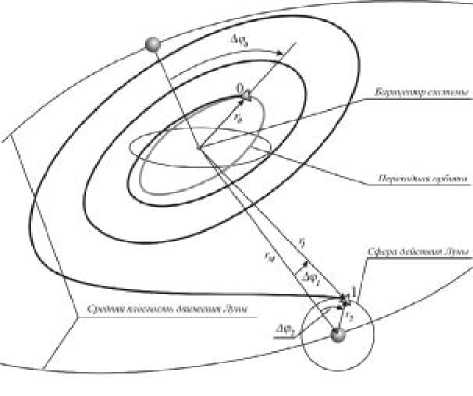
Рис. 1. Второй и третий участки траектории. Схема преобразования фазовых координат из одной системы в другую

Vr 2 = Vrp ^{cos ( A} , 2 ^{— A} , ) + V p sin ^{( a} , ^{— A} , ) , V₉ 2 = ^V, p CoS ^(A , 2 ^{— A} , ) - Vrp Sin ^(A , 2 ^{- A} , i ) .

Здесь ^Vrp

= Vr 1 ^-_A P M" ^Si n ^(A , 1 ) и r_M

VW = V , 1 — 1 PM^ COs ^(A , i ) r_M

– радиальная и

трансверсальная составляющие компоненты скорости относительно Луны в барицентрической системе координат, r ₁ – радиус-вектор, определяющий положение космического аппарата относительно барицентра системы, r ₂ – радиус-вектор, определяющий положение космического аппарата относительно Луны, r_M – радиус-вектор, определяющий положение Луны относительно барицентра системы (если принять орбиту Луны круговой, то радиус – величина постоянная), A,1 - угол между векторами r_M и r , A,2 - это угол между векторами r и — r_M .

После преобразования фазовых координат КА рассчитывается маневр формирования селеноцентрической околокруговой орбиты. Учитываются возмущения от гравитационных воздействий Земли и Солнца. Если считать плоскость орбиты постоянной уравнения движения имеют вид:

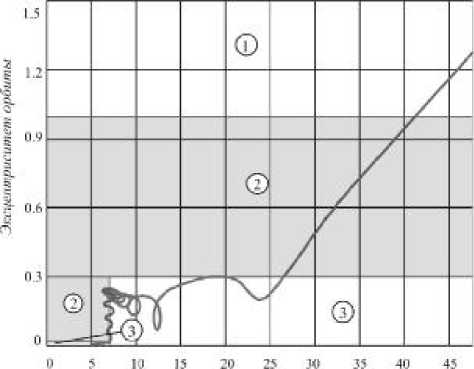
Ceieaotu'rimpMWMiu portuw, тыс kw

Рис. 2. Области действия законов управления на этапе формирования селеноцентрической орбиты: 1 – область торможения по закону (4); 2 – область уменьшения эксцентриситета по закону (5); 3 – область уменьшения радиуса перицентра по закону (6)

dr

r

dt

du _ V,

^, dt r ^,

dVr dt

,

^^^^^^в

r

"7 ⁺

a 0 §

-- COS X + f ,

dV, dt

^^^^^^в

к к r ,

+

r

a0 §

^{0 Sin X +} f, ,

dm _ a ₀ § dt c ^.

Здесь u – аргумент широты; r – радиус-вектор, определяющий положение КА относительно центра Луны; V_r , V, составляющие безразмерного вектора скорости космического аппарата относительно центра Луны; a ₀ – номинальное безразмерное ускорение двигателя; c – безразмерная скорость истечения рабочего тела; § -функция включения-выключения двигателя; m = т_РТ m0₀ относительный расход рабочего тела; f = f_z + f S - суммарное возмущающее ускорение, f_Z и f_S возмущающие ускорения от гравитационных полей Земли и Солнца.

Точное решение задачи оптимального управления на этом участке движения затруднительно, из-за сложности возмущающих ускорений и

значительных вариаций условий входа в сферу действия Луны. В данной работе предложен подход, связанный с интерактивным формированием закона управления в зависимости от отклонений текущих оскулирующих элементов орбиты от требуемых значений. Значения оскулирующих элементов орбиты: эксцентриситета e , радиуса перигея Г _п , большой полуоси A и угла истинной аномалии 3 в каждый момент времени могут быть рассчитаны при известных фазовых координатах КА по формулам:

e = /rV r ² — 1 ) 2 + ( rVV , ) 2 ,

2 r 2 _V

r п               ,

1 + e

г

A = —^

1 — e ’

sin 3 =

rV У r ,

cos 3 =

rV_r ²

e

e

Известны законы управления, полученные Лебедевым [2] для оптимальных по быстродействию маневров изменения одного их элементов орбиты. Используя комбинацию этих законов можно получить требуемые значения оскулиру-ющих элементов в конечный момент времени.

На начальном этапе движения, непосредственно после входа в сферу действия планеты (до достижения эксцентриситета меньше 0,95), используется тангенциальный закон управления, уменьшающий скорость аппарата:

tgX =

п

В дальнейшем, если велико отклонение эк-

сцентриситета от требуемого, то ускорение от тяги двигателей направлено так, чтобы обеспечить наибольшую скорость уменьшения эксцентриситета:

tg ^ = -

e cos ² 9 + 2cos 9 + e sin 9 (1 + e cos 9 )

если велико отклонение перицентра орбиты от требуемого, то используется закон управления, обеспечивающий наибольшую скорость уменьшения радиуса перицентра:

tg X =

1 + e cos 9 e sin 9

На рис. 2 показаны области действия этих законов управления, линии их переключения и пример фазовой траектории КА при формировании околокруговой селеноцентрической орбиты с требуемыми параметрами r _n = 5000 км, e = 0,05 .

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ

Моделирование движения КА сводится к решению задачи Коши для системы дифференциальных уравнений (2) с начальными условиями (1) и законами управления, определяемыми соотношениями (3) – (6). Для ее численного решения использовался метод Рунге-Кутты 4 порядка с постоянным шагом.

Проектные параметры выбраны близкими к параметрам исследовательского КА Европейского космического агентства “SMART-1”: масса на орбите выведения m ₀ = 600 кг, P = 0,1...0,2 Н, c = 15 км/с. Считается, что КА формирует селеноцентрическую орбиту с начальными условиями, полученными в результате решения задачи пролета Луны на заданном угловом расстоянии с не фиксированным вектором скорости [3].

После достижения сферы действия Луны фазовые координаты КА пересчитываются из барицентрической в селеноцентрическую систему координат по формулам (1).

Интерактивное управление на этом участке движения определяется в соответствии с описанной методикой (рис. 2), предполагается, что двигательная установка работает без выключений.

Движение КА моделируется до необходимого конечного радиуса перицентра окололунной орбиты.

Было проведено моделирование для большого диапазона расстояний от КА до Луны и селеноцентрической скорости в начальный момент времени. Были выявлены следующие закономерности селеноцентрического движения КА:

• -    попадая в сферу действия Луны КА быстро начинает тормозить по закону (4) до достиже-

• ния скорости, обеспечивающей замкнутую траекторию в сфере действия Луны;

• -    затем уменьшается эксцентриситет орбиты до значения e = 0,3 ;

• -    затем чередуются законы управления (5) и (6) и последовательно уменьшается эксцентриситет и большая полуось.

На рис. 3 показан один из вариантов такого закона изменения Л 1 ( t ) , обеспечивающего формирование селеноцентрической орбиты для не оптимального вектора скорости входа в сферу действия Луны. На рис. 4 показана соответствующая траектория движения.

Продолжительность формирования селено-

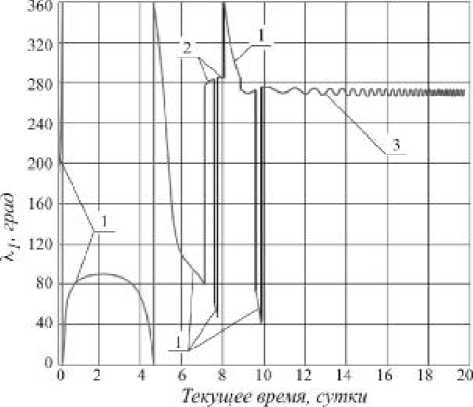
Рис. 3. Закон управления для формирования околокруговой селеноцентрической орбиты, T 3 = 19,5 сут, e = 0,09, r = 5000 км

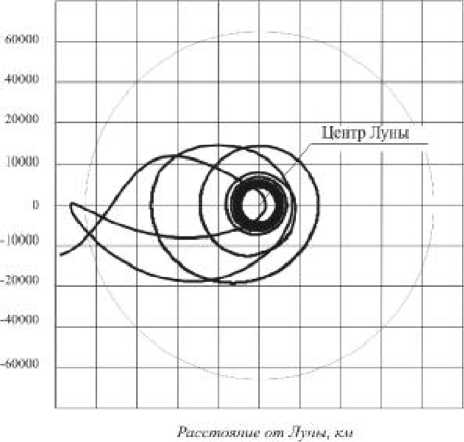
Рис. 4. Траектория селеноцентрического движения КА, соответствующая управлению на рис. 3. В начальный момент времени вектор скорости не оптимален

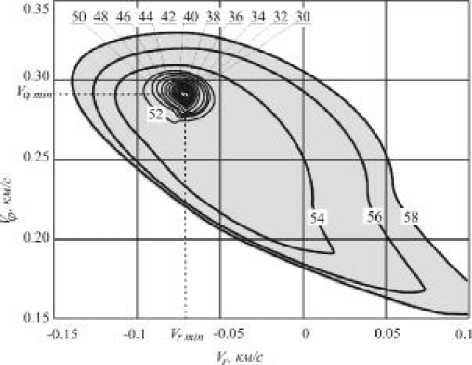
Рис. 5. Изолинии длительности маневра (сут) для КА с параметрами P = 0,1 Н, r0 = 66000 км, rk = 5000 км центрической орбиты существенно зависит от направления и величины начальной скорости КА.

Удалось приближенно определить компоненты скорости, которые являются оптимальными с точки зрения быстродействия:

( V r min , ^V p min ) = ^arg ^min T ( V r 0 , V p 0 ) . (7)

Поскольку двигатель в сфере действия Луны работает без выключений и секундный расход топлива – величина постоянная, найденные значения ( V r min , V p min ) соответствуют минимальному расходу рабочего тела.

На рис. 5 представлены изолинии длительности маневра формирования околокруговой селеноцентрической орбиты с начальным радиусом, равным среднему радиусу сферы действия Луны (66000 км). Серым цветом выделена область допустимых значений компонент скорости входа. Если вектор селеноцентрической скорости не принадлежит этой области, то для этого закона управления и уровня реактивного ускорения формирование заданной селеноцентрической орбиты невозможно. В этом случае, КА покидает сферу действия Луны.

Наименьшая продолжительность маневра

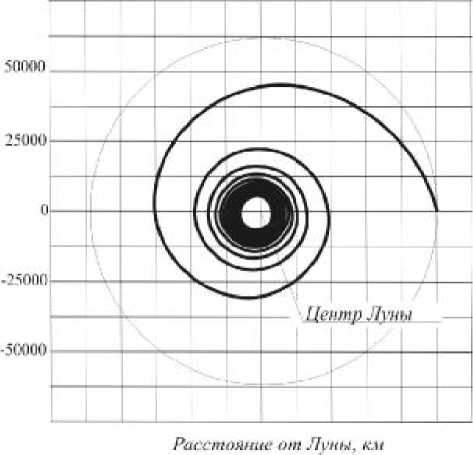
Рис. 6. Траектория формирование околокруговой селеноцентрической орбиты с радиусом перигея 5000 км, T=28,5 сут, P = 0,1 Н, е = 0,09, m = 16,4 кг. Оптимальный вектор скорости входа

( T = 28,5 сут) получена при следующем значении составляющих вектора скорости входа ( V min , V p min ) = ( - 0,074; 0,292 ) . На рис. 6 показана траектория селеноцентрического движения, соответствующая этому оптимальному вектору скорости. Видно, что траектория имеет традиционную для КА с двигателем малой тяги спиральную форму. На оптимальной траектории практически нет участков с законом управления (5), который обеспечивает уменьшение эксцентриситета.

В табл. 1 показаны проектно-баллистические параметры селеноцентрического движения КА для различных начальных условий. Были получены оптимальные значения скорости, продолжительности полета и расхода рабочего тела. Эти значения могут использоваться для комплексной оптимизации перелетов в системе Земля-Луна, совершаемых аппаратом с двигателем малой тяги. Изолинии длительности

Таблица 1. Проектно-баллистические параметры формирования селеноцентрической орбиты

Начальный радиус, км Оптимальные составляющие вектора скорости, км/c Время перелета, сут Расход рабочего тела, кг Vr min , км/c V ■       / ' pmin , км/c r = 66000 -0,074 0,292 28,5 16,4 r = 56000 -0,071 0,315 24,8 14,2 r = 46000 -0,045 0,337 19,5 11,2 маневра, показанные на рис. 5, соответствуют первой строке табл. 1.

ЗАКЛЮЧЕНИЕ

Использование интерактивного управления обеспечивает формирование околокруговой селеноцентрической орбиты в широком диапазоне начальных условий. Предложенная методика может быть использована для решения задач формирования заданных окололунных орбит.