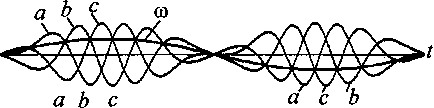Формирование сигналов заданий следящим преобразователям частоты в электроприводе

При разработке микропроцессорной системы управления асинхронным двигателем (АД) с фазным ротором нам потребовалась трехфазная симметричная система импульсов переменной частоты с реверсом, для чего мы использовали тригонометрические функции:

а = sin(wt), b = sin(w/ - 2 тг/З), _п.

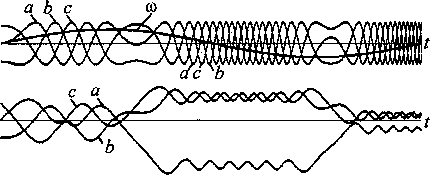
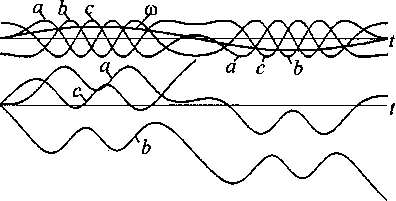
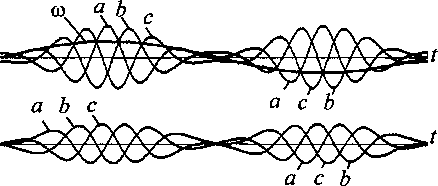
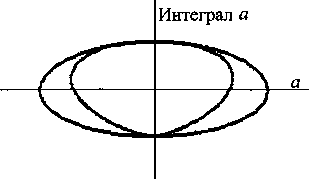
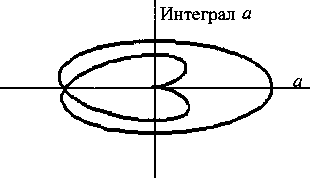
c = sin(wt + 2 тг/З) 2 и следили за их моментами переходов через нуль. Первые же эксперименты на ЭВМ при линейном (пуск двигателя) и синусоидальном изменении скорости задания

Рассмотрим момент времени t₀ где-то в середине процессов (см. рис. 1) после их начала при t = 0. В этой точке величину задания обозначим ®₀, а его производную или наклон со^. Введем новый смещенный по времени аргумент т = t - t₀. Предположим, что с момента т = 0 задание продолжит изменяться по линейному закону с указанным наклоном. Тогда формула (1) только для а запишется и преобразуется следующим образом:

а = sin[(w0 + Ыо'тЖ + т)] =,~

= 8Н1[(ыо + ыоЧо)7+ыо^о+Уо'т2].'

Первый член под обозначением синуса в преобразованной формуле назовем «мгновенной частотой» на момент /0:

По = Wo + Wq^o-(3)

Второй член в правой формуле (2) - постоянный на момент /0 угол сдвига, а последним членом можно пренебречь из-за малости величины т2. Из формулы (3) видим, что с увеличением времени все больше сказывается величина производной сигнала задания <оо'. Это подтверждает и эксперимент на ЭВМ (см. рис. 1), где поведение сигналов соответствует формуле (3), когда все большую роль играет производная задания. Поэтому «очевидные» формулы (1) не применимы для решения поставленной задачи, но физика процессов на рис. 1 сверху стала понятной.

Выход из ситуации нам подсказал использованный в рассуждениях идеальный трехфазный фазовращатель на АД с фазным ротором, в котором поворот фазы определяет угол поворота ротора ф, а не скорость. При постоянной скорости АД ведет себя как идеальный преобразователь частоты. Угол определяется интегралом скорости с точностью до постоянной интегрирования С:

Ф= рос// + С.                            (4)

Теперь формулы (1) перепишутся в другом виде:

а = зт(ф), 6 = 8ш(ф-2тг/3), с = 8Н1(ф+2л/3).

При постоянной скорости СО = const формулы (5) преобразуются в свой частный случай - в формулы (1). Диаграммы эксперимента на ЭВМ по формулам (4) и (5) приведены на рис. 2.

Так были получены трехфазные частотнорегулируемые аналоговые сигналы (5), моменты переходов через нуль которых определили нам фронты искомых импульсов. Сразу же возникла вторая более общая задача формирования аналоговых сигналов заданий следящим преобразователям частоты с нагрузкой в виде электромагнитных исполнительных устройств (трансформаторов, двигателей). Мы должны исключить возможность насыщения магнитопроводов этих устройства и обеспечить их перемагичивание по симметричным циклам. Такое требование следует применить и к электрическим машинам, хотя неприятные последствия несимметричного перемагничивания в них значительно ослаблены воздушным зазором. Магнитная индукция в магнитопроводе трансформатора изменяется примерно пропорционально интегралу приложенного к его обмотке напряжения. На рис. 1 и 2 снизу приведены диаграммы интегралов сигналов а, Ъ, с (или индукций в магнитопроводах), обозначенные теми же буквами.

Видим, что никакой электромагнитный аппарат не выдержит таких напряжений, как сигналы по формулам (1) и (5), на своих обмотках.

В частотно-регулируемом приводе переменного тока по сути такая же проблема давно решена подачей на обмотки напряжений, пропорциональных их частоте. Для сигнала а (не будем далее писать формулы со сдвигами для фаз b и с) формула (5) запишется в виде:

а = шsin (ф) . (6)

Результаты эксперимента с формулами (4) и (6) приведены на рис. 3.

Здесь интегралы (индукции) оказались смещенными на постоянные величины, которые скомпенсированы выбором ненулевых начальных значений интегралов или постоянных интегрирования С в (4), что видно на левой границе нижнего рис. 3. Теперь мы получили приемлемые значения индукции на нижних диаграммах, но моменты переходов через нуль сигналов на верхних диаграммах отличаются от таковых на рис. 2. Что делать, если мы имеем два приемлемых разных решения исходной задачи?

Продолжим рассуждения. Ничто не мешает нам в приведенных выше формулах заменить синусы на косинусы с тем же результатом. Эксперименты на ЭВМ подтвердили это. Но тогда формулы (6) являются производными от формул (5). Когда надо отделить постоянную или медленно изменяющуюся составляющую в сигнале, надо продифференцировать его! Продолжим дифференцирование, сформируем следующий вид сигналов задания (7) как производные от сигналов (6):

а = dto[ dt • sin (ф) + со² cos (ф). (7)

Полученные на ЭВМ диаграммы сигналов по формулам (4) и (7) показаны на рис. 4.

Мы получили уже третье «инженерно приемлемое» решение первой, дискретной задачи и второе решение следующей, аналоговой. Последние диаграммы на рис. 4 более приятны. Например, в отличие от рис. 3 снизу процессы начинаются и кончаются нулевыми начальными значениями или с размагниченных магнитопроводов. Задавать правильные начальные индукции на рис. 3 снизу -сложная инженерная задача.

Для двух последних предложений (6) и (7) на рис. 5 построены фазовые траектории зависимо-

Рис. 1. Сигналы по формулам (1) сверху и их интегралы снизу при синусоидальном изменении си

Рис. 2. Сигналы по формулам (4), (5) сверху и их интегралы снизу при синусоидальном изменении си

Электромеханика

Рис. 3. Сигналы по формулам (4), (6) сверху и их интегралы снизу при синусоидальном изменении ш

Рис. 4. Сигналы по формулам (4), (7) сверху и их интегралы снизу при синусоидальном изменении ш

Рис. 5. Фазовые траектории сигналов и их интегралов за первый полупериод изменения ш для рис. 3

стей интегралов сигналов (индукций) от самих сигналов (почти напряженностей). Эти траектории имеют родство с петлями гистерезиса, они характеризуют процессы в магнитопроводах.

И опять фазовые траектории для сигнала по формуле (7) и рис. 4 получились самые приятные для «инженерного взгляда».

Рис. 6. Фазовые траектории сигналов и их интегралов за первый полупериод изменения w для рис. 4

Выводы

Сигналы заданий следящим преобразователям частоты можно формировать по формулам (4) -(7), но ни в коем случае по «очевидной» формуле (1). Результаты получились различными, поэтому требуется дополнительный анализ наших «инженерных» предложений.