Формирование спектров брэгговского отражения света от фотоннокристаллических структур

В связи с развитием оптоэлектроники огромное практическое значение приобретают исследования структур, позволяющих управлять распространением света [1]. К числу таких структур относятся фотонные кристаллы (ФК). Особый научный интерес к ФК обусловлен тем, что они представляют собой объекты, позволяющие проводить исследования, касающиеся фундаментальных аспектов взаимодействия света с конденсированной средой [2].

ФК — пространственно-периодические твердотельные структуры, период которых сравним с длиной волны видимого света. Тот факт, что период решётки ФК сравним с длиной волны видимого света, модифицирует поведение фотонов в таком кристалле по сравнению с их поведением в обычном кристалле. В данной работе объектами исследования являлись трёхмерные ФК с симметрией гранецентрированной кубической решётки. К таким кристаллам относятся опалы и полимерные опалоподобные структуры на основе полистирола, речь о которых, как об объектах экспериментального исследования, идёт в настоящей работе.

В процессе получения опалоподобных ФК происходит самоорганизация структурных элементов (сфер диоксида кремния и полистирола для опалов и полимерных ФК соответственно) в плотноупа-кованную гранецентрированную кубиче- скую решётку. Отметим, что структура получаемых ФК, как правило, не является строго идеальной. Во-первых, происходит взаимное спекание сфер, а во-вторых, сжатие структуры в направлении осаждения на подложку, что приводит к преобразованию сфер в сфероиды и понижению симметрии решётки [3]. Эти отклонения в соответствии с работой [3] можно характеризовать двумя параметрами: X = 1 — a00 / Dl — коэффициентом изотропного спекания и п = D^/Dl — коэффициентом сжатия вдоль направления [111], где a00 — расстояние между ближайшими сферообразными частицами в латеральной плоскости (плоскости (111)) образца, Dl — размер сферообразных частиц в латеральной плоскости образца, D^ — размер сферообразных частиц в кристаллографическом направлении [111] (рис. 1).

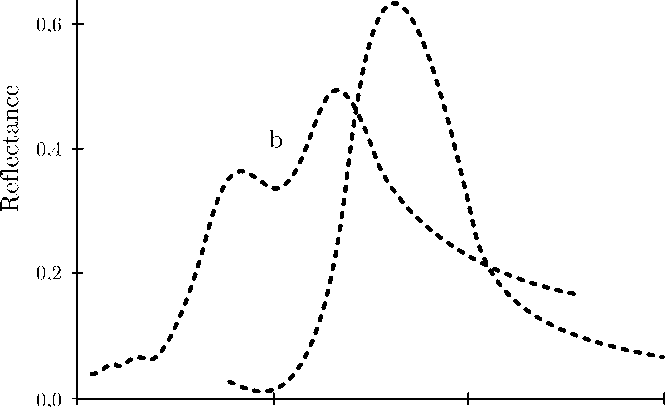
Отличительной особенностью рассматриваемых ФК является то, что вблизи некоторого характерного угла падения света θ на отражающую кристаллическую плоскость наблюдается ярко выраженная дублетная структура брэгговского пика (рис. 2, сравним кривую a для 9 = 42 ° с кривой b для 9 = 55 ° ).

Спектры брэгговского отражения света изучались на оптической установке, собранной на базе спектрометра МДР-23 с рабочим спектральным диапазоном 400-850 нм и обратной линейной дисперси- ей 13 ˚A/мм. Источником белого света служила лампа накаливания, луч от которой коллимировался с помощью диафрагмы и линзы так, что угол сходимости пучка не превышал 3°. Световой пучок направлялся на образец, закреплённый на гониометре от эллипсометра ЛЭФ-3М. Установка обеспечивала точное позиционирование кристалла: выбор нужного угла падения светового потока и азимутальную ориентацию образца (относительно вращения в латеральной плоскости). Отраженный от поверхности образца свет через систему линз направлялся на входную щель спектрометра, ширина которой варьировалась в пределах 100–200 мкм. Световой поток на выходе спектрометра регистрировался с помощью фотоэлектронного умножителя ФЭУ-79 в режиме счета фотонов, электрический сигнал после прохождения через предусилитель и блок сопряжения обрабатывался персональным компьютером, а записанный спектр в цифровом виде сохранялся в файле.

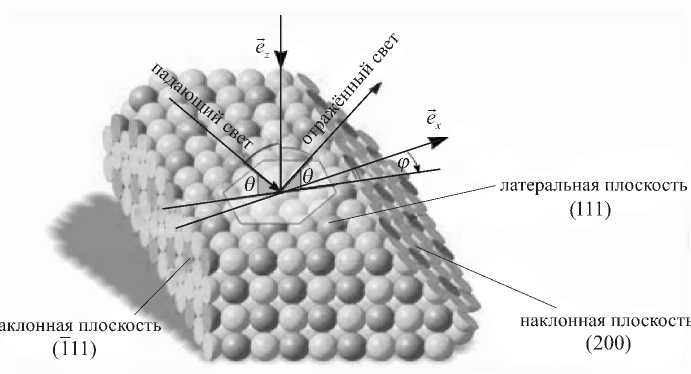
Рис. 1. Геометрия отражения света от поверхности ФК. Азимут ϕ

считается равным нулю в том случае, когда плоскость падения света — перпендикулярна линии пересечения плоскостей (111) и (111)

0,8

а

400                 450                 500                 550

X (пт)

Рис. 2. Экспериментальные спектры брэгговского отражения света от полимерного (на основе полистирола) опалоподобного ФК для s -поляризованного света для углов падения света 9 = 42 ° (а) и 9 = 55 ° (b)

Теоретическая модель, используемая для объяснения наблюдаемой экспериментально картины, основана на формализме блоховских волн, в рамках которого электрическое поле электромагнитной волны внутри ФК представляется в виде суперпозиции блоховских мод:

Ё (^ = E E**)- к где

Ёк(т) = E А(к - G)ei(k-G)•к.

G

Здесь к — волновые векторы соответствующих блоховских мод, <5 — векторы обратной решётки, А — амплитудные коэффициенты разложения блоховских мод по плоским волнам. Введение таких мод возможно благодаря наличию в ФК трансляционной симметрии. По этой же причине можно разложить диэлектрическую проницаемость в ряд Фурье по векторам обратной решётки:

6(r) = E eG eG "•

G

Подстановка выражения для блоховской волны в уравнения Максвелла даёт уравнение для напряжённости электрического

ТРУДЫ МФТИ, 2009, Том 1, № 1 поля в ФК:

(к2 - к2е о) а (к) -к (к • 5(к )) == к2 E ЕвЯ(к- G),

<5=о где

к о = -• c

Для получения точного решения при помощи метода плоских волн необходимо использовать бесконечное число векторов обратной решётки. Ключевой момент состоит в том, что для правильного качественного описания экспериментально наблюдаемой картины в области видимой части спектра нет необходимости учитывать все векторы обратной решётки [4], а достаточно использовать только два из них, соответствующих системам кристаллографических плоскостей (111) и (111) (рис. 1). В таком случае при нулевом азимуте ф плоскости падения света дисперсионное уравнение разделяется на два независимых уравнения, соответствующих TE- и TM- собственным модам.

Когда модуляция диэлектрической проницаемости бесконечно мала ( 6 5 111 ^ 0 , ^E(G in ^ 0 — приближение пустой решётки), дисперсионное уравнение может быть решено аналитически. Соответствующий энергетический спектр приведён на рис. 3.

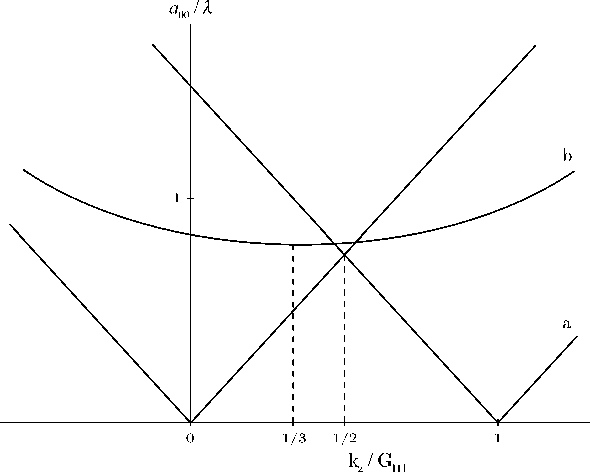
Рис. 3. Дисперсионные кривые собственных мод в ФК в приближении пустой решётки, соответствующие дифракции света на латеральной плоскости (111) (а) и наклонной по отношению к поверхности ФК плоскости (111) (b)

На рис. 3и последующих рисунках λ — длина волны света в вакууме, k _z — проекция волнового вектора собственной моды на нормаль к поверхности, G 111 — длина вектора обратной решётки в направлении [111] .

При расчёте энергетических спектров собственных мод электромагнитного поля использовались характерные значения параметров полимерных опалоподобных ФК [3]. Как и предсказывает теоретический расчёт, при нулевом азимуте ϕ можно выделить дисперсионные зависимости для TE- и TM-мод (соответствующих s -и p -поляризациям падающего света).

Как для одной, так и для другой группы кривых наблюдается возникновение стоп-зоны. При этом для некоторого угла падения света (соответствующего выполнению условия многоволновой дифракции [4]) внутри стоп-зоны появляются разрешённые состояния (рис. 4), связанные с переносом энергии внутри ФК. Такие со- стояния приводят к появлению провала в пике брэгговского отражения и возникновению дублетной структуры, наблюдаемой экспериментально.

Как видно из сопоставления модельных спектров брэгговского отражения (рассчитанных без учёта затухания) и дисперсионных зависимостей (рис. 5), положение провала в пике брэгговского отражения действительно соответствует разрешённым состояниям, возникшим из-за дифракции на плоскости (111) . Неполное отражение света в области фотонной запрещённой зоны связано с тем, что мнимая часть волнового вектора затухающей моды оказывается не перпендикулярной по отношению к наклонным (рис. 1) фотоннокристаллическим плоскостям. В том случае, когда учитывается только дифракция на латеральной плоскости, внутри стоп-зоны не возникает разрешённых состояний и вместо дублетной структуры расчётный спектр даёт одиночный пик брэгговского отражения.

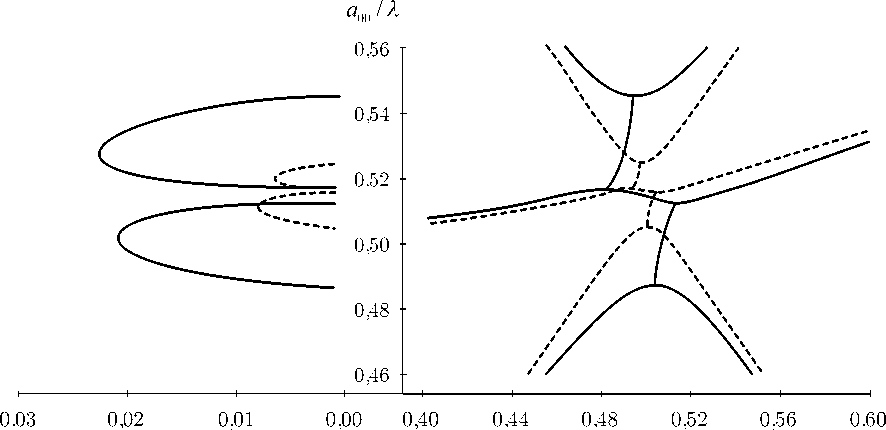
1ш kz / Gin Re kz / Gni

Рис. 4. Энергетические спектры собственных мод электромагнитного поля в полуогра-ниченном ФК для угла падения света 9 = 57 ° и азимута ^ = 0 ° . Сплошные кривые — для s -поляризованного света, штриховые кривые — для p -поляризованного света

При других углах падения, заметно отличающихся от 6 = 57 ° (когда дисперсионная кривая, соответствующая дифракции на системе плоскостей (111) , не попадает в стоп-зону плоскостей (111) ), для правильного описания наблюдаемой экспериментально картины достаточно учитывать лишь дифракцию на латеральной плоскости.

В случае азимута ϕ, отличного от нуля, собственные моды обладают не линейной, а эллиптической поляризацией. Это приводит к тому, что при падении на поверхность ФК s- и p-поляризованного света отражённая волна становится эллиптически поляризованной.

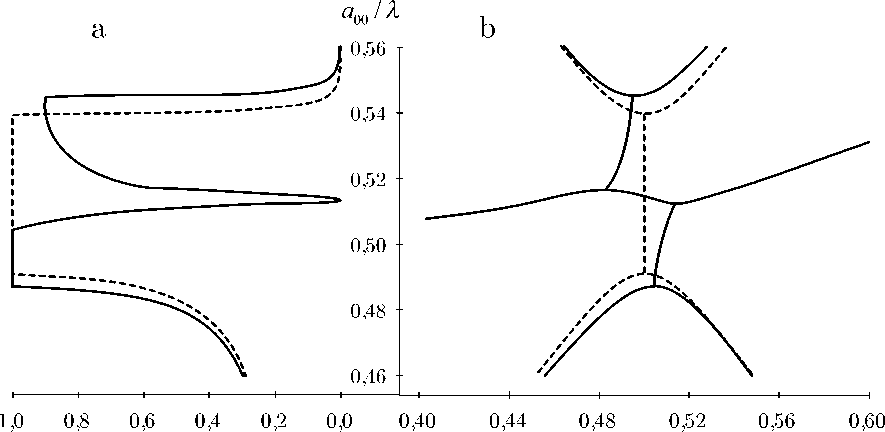
Reflectance Re kz / Gni

Рис. 5. Рассчитанные спектры брэгговского отражения света (a) и соответствующие дисперсионные зависимости (b) для собственных мод электромагнитного поля в по-луограниченном ФК для угла падения света 9 = 57 ° и азимута ^ = 0 ° . Сплошные кривые — для дифракции света на двух системах кристаллических плоскостей (111) и (111). Штриховые кривые — для дифракции света только на одной системе кристаллических плоскостей (111)