Формирование суб-пикосекундных плазмон-поляритонных импульсов в процессе кооперативного распада экситонов квантовых точек вблизи металлической поверхности

Оптическое сверхизлучение (СИ) долгое время является предметом пристального изучения как с теоретической, так и с экспериментальной точек зрения [1-3]. Уже в первых экспериментальных работах [2] была отмечена высокая степень когерентности такого излучения, а. также возможность генерации коротких мощных импульсов в газовых средах при сравнительно несложной схеме эксперимента.

Дополнительные перспективы практического использования эффекта возникли после экспериментального наблюдения режимов СИ в конденсированных средах [4, 5]. В этих работах были достигнуты новые характерные масштабы длительности и мощности генерируемых импульсов СИ, обусловленные существенно большими по отношению к газовой среде

«Московский физико-технический институт (государственный университет)», 2018

концентрациями квантовых излучателей. Вместе с тем при размещении плотного ансамбля квантовых излучателей в диэлектрической среде-носителе возникла необходимость учета влияния макроскопического окружения на особенности развития коллективной квантовой динамики [6] системы, а также влияния диполь-дипольных взаимодействий на скорость релаксационных процессов [7] в ней.

Новые возможности известного эффекта СИ могут быть связаны с реализацией коллективных эффектов в процессе генерации поверхностных волн — поверхностных плазмон-поляритонов (ППП) в процессе когерентного распада экситонов полупроводниковых квантовых точек (КТ) вблизи металлической поверхности [8,9]. Полупроводниковая КТ представляет собой нульмерный объект, в котором эффекты размерного квантования приводят к ярко выраженному дискретному спектру электронов. Основная сложность практического наблюдения коллективной динамики ППП в таких системах [10] связана с большими значениями скорости затухания ур возбуждений на границе металл-диэлектрик, в результате чего исследуемые когерентные коллективные процессы могут быть частично или полностью маскированы некогерентными. Технически вопрос может быть решен путем существенного увеличения концентрации КТ вблизи металлической поверхности, при котором скорость накачки в ППП в процессе распада экситонов КТ окажется значительно большей скорости затухания ППП. Однако возникающий в таком случае одновременный рост скорости излучательной релаксации для КТ [7] способен привести к нежелательной в условиях данной задачи перекачке энергии в излучательные (некогерентные) моды. Таким образом, задача заключается в оптимизации параметров волноводного спазера [11], при которых скорость развития коллективных эффектов для плазмон-поляритонов превышает скорость их затухания, и при этом система не теряет своей когерентности.

В настоящей работе рассматривается модель волноводного спазера, включающая в себя нанесенную на поверхность металла (золото) диэлектрическую пленку, легированную полупроводниковыми оболочечными КТ CdSe/ZnS, выбор размера которых выполнен с учетом условий резонанса между энергиями межзонного перехода в КТ и возбуждаемых на границе металл/диэлектрик ППП [12]. Предсказана возможность генерации суб-пикосекундных плазмон-поляритонных импульсов в условиях развития коллективных эффектов в волноводном спазере. Экспериментальная реализация модели связана с решением задачи оптимизации положения КТ над металлическим зеркалом для достижения максимальной эффективности преобразования энергии возбужденной КТ в ППП [13].

• 2.    Формирование коллективных состояний волноводного спазера.Основные соотношения

Предполагаем, что схема эксперимента включает в себя интерфейс в виде волновода металл/диэлектрик [14] с синтезированными внутри тонкой диэлектрической пластинки оболочечными квантовыми точками CdSe/ZnS [15] с шириной запрещенной зоны ядра Е_д = 1.76 эВ (при 0 К)) — на рис. 1(a). Формирование сверхизлучательного сигнала с длиной волны Х дрр с частотой ш для геометрии с рис. 1 может происходить в результате коллективного распада экситонов возбужденных состояний квантовых точек на соответствующей межзонному переходу 15(е) ^ 15(^) частоте ш_а = Еі д (_е)-і д ( ^ ) / ~ = 2тгс/А_а (1 — основной уровень из валентной зоны и 2 — возбужденный уровень из зоны проводимости) и, при условии г ^ Х_а, передаче части этой энергии поверхностным плазмон-поляритонам [8]. При этом локализация процесса в направлении Оу может быть осуществлена при помощи системы дополнительных волноводов, работающих по принципу брэгговского отражения плазмонов (ARROW, antiresonant-reflecting optical waveguide [16]). Рассматриваемая ситуация существенно отлична от известной схемы излучающего спазера, когда под действием внешней накачки дипольные моменты излучателей (дефектов) ориентируются коллинеарно границе металл/диэлектрик, и происходит генерация перпендикулярного этой границе узконаправленного оптического пучка [17].

Рассматривая задачу в трехмерном приближении, считаем, что толщина слоя диэлектрика с КТ Һ существенно меньше длины затухания l d плазмона в на правлении оси Oz. Характерный объем квантования задачи равен V = А„, г де L_x = L_p = L _z = А_а и выбирается, в основном, из области расположения диэлектрика, считая глубину проникновения поверхностной волны в металл пренебрежимо малой. Кроме того, справедливо условие А_а ^ а, что позволяет оставаться в пределах дипольного приближения для квантовых точек с характерным радиусом а.

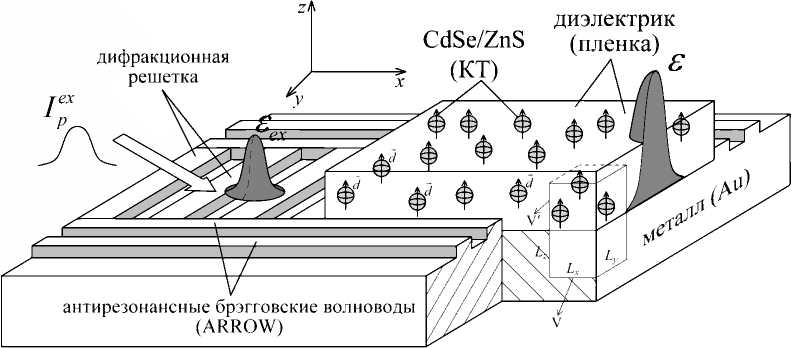
Рис. 1. Схема, формирования ППП-импульсов в металл/диэлектрик волноводе с накачкой CdSe/ZnS КТ [20]

Считая, что показатель преломления диэлектрического окружения КТ является комплексной величиной п = пд + ini, п = Де, где е — комплексная диэлектрическая проницаемость, описание системы может быть построено аналогично модели локализованного спазера (квантовая точка) + наночастица [18] с помощью уравнений для матрицы плотности р ансамбля двухуровневых КТ в виде

Г

(1а)

Р12 = -(iA_e + — )Р12 + (i^0 + i^URР12 + ^oniР12) П21,

ТГ21 = 2і (^оР12 - П*Р21) - 4^оПі |Р12|2 - Ге (1 + п21) ,                   (16)

где введены новые эффективные   параметры [19] скорости   релаксации

Г = ra(nRlR - nili + 2гГ^li) и частоты отстройки Ae = 6a(lR - 2^(niIr + пдli)) + Aa для KT, Aa = ша - ш, п21 = Р22 - Р11, а частота Раби может быть представлена как

По = 9Е • aJ l R + li

через константу связи д = ^12

/S-7(~Ed^мW)

и нормированное поле

А ру/ e_deoV d^ / (~S_n)

е

с амплитудой Ар папряжешюсти поля ППП: Ц12 соответ ствует величине дипольного момента межзонного перехода; 5а представляет собой ма лую поправку за. счет лэмбовского сдвига. Полученные соотношения являются след ствием представления частоты Раби ближнего поля в виде П = - (АпVppi2£p) /~ где

а_п = ynSj^dH)

у определяет скалярный потенциал поля, е = у Np. Np — коли

чество ППП в области взаимодействия. Нормировка мод спазера J |Vy |² dV = 1 [20] в

итоге и приводит к выражению П = Ц12

S_n/ (~E_dE₀V'^ У<е = де. Коэффициент Бергмана

S (ш) = Re (E_d/(E_d - е_т (ш))) характеризует границу раздела металл/диэлектрик [18], тогда

как параметры E d 11 е_т (ш) = 1 - шр/ (ш² + іузш) являются диэлектрической проницаемо

стью диэлектрика и металла, соответственно; здесь ys — столкновительная частота электронов в металле, шр = 4лпте2/то — плазменная частота в металле с массой электронов то при их концентрации nm. Дисперсионная u д = (IrEr + liEi) / (eR + E2) и диссипативная поправки ni = (liEr — IrEi) / (eR + E2) выражаются через действительную er и мнимую Ei части диэлектрической проницаемости среды-носителя [19] и имеют физический смысл дополнительных частотной модуляции и эффектов поглощения (ni < 0) либо усиления (ui > 0) за счет учета локального поля соответственно. Здесь l(n) — комплексная функция l (п) = Ir + Hr для которой Ir = (nR — п|) /3, li = 2пдni/3.

Для перехода к самосогласованной задаче система (1) должна быть дополнена уравнением распространения для частоты Раби поля, формируемого на границе сред:

^ о = — ^2 Р12 — 7р^0,

где £д =

1 g V N

_ / to d^ V S „ ^ 12 N

определяет характерное время установления квантовых кор

реляций в тонком слое вблизи границы металл/диэлектрик, где N_a — количество, а N

— концентрация КТ. Необходимо отметить, что скорость затухания плазмонной моды 7Р = 1/tj + 1/tr очень велика, и определяется хара.ктерпым временем радиационных tr и джоулевых tj потерь. В условиях 1/tj ~ 30/tr [9] радиационные потери можно не учиты вать, а. джоулевы задаются столкновительной частотой металла.

Для решения задачи оптимизации размеров КТ в условиях точного резонанса А_е = 0 воспользуемся известной зависимостью энергии перехода 15(е) ^ 15 (К) от их диаметра D qd = 2а:

~2я2 / 1      1       3.56 • е2

E1S(c)-1S(h) = Eg + 2^qd ^ + —) — ETdQD- где е — заряд электрона, т; и т^ — эффективные массы электрона и дырки в объеме материала КТ с диэлектрической проницаемостью E. Для CdSe соответствующие параметры составят т; = 0.125то, т^ = 0.43то и e = 10, в соответствии с чем размер ядра КТ составит Dqd = 4.3 нм. Величина дипольного момента соответствующего межзонного перехода КТ составит ц = Ц12 = 0.31 • 10-28 К л • м [18]. Оптимизация параметров системы для настройки к условиям плазмон-экситонного резонанса осуществлялась с использованием веб-приложения расчета, уровней квантовой точки собственной разработки [21].

На рис. 2 представлены результаты численного моделирования системы (1) - (2) при различных значениях концентрации КТ и параметров содержащей их среды-носителя. Пороговое значение концентрации КТ соответствует ситуации, когда, скорость развития коллективных процессов в системе приблизительно равна, скорости диссипативных процессов и составляет 2 • 10²² с^-1. Необходимо отметить, что скорость диссипативных процессов определяется скоростью затухния плазмонов в металле у_р и скоростью затухнаия экси-тонных возбуждений Г_е. При значениях концентрации, ниже пороговых, коллективные эффекты уступают по скорости диссипативным процессам в металле и ППП-импульс затухает (пунктирная линия 1, рис. 2). При значениях концентрации выше пороговой ППП-импульс формируется, но действие диссипативных процессов приводит к существеному уменьшению интенсивности ППП-импульса (штриховая линия 2, рис. 2). Наконец, выбором среды носителя с заданным сочетанием параметров n i и п д можно добиться (в теории, см. [22]) полной компенсации величины Г_е, что приводит к значительному росту интенсивности сформированного ППП-импульса. В частности, с выбранными параметрами и при учете концентрации КТ N = 3 • 10²² м^-3 характерное время развития коллективных процессов составит 1 д = 157 фс при количестве N_a = 3.75 • 103 КТ в области взаимодействия с линейными размерами ~ А. Длительность сформированного моноимпульса оказывается равной 1 д = 1.87 пс для представленного на рис. 2 случая (3). В практическом плане представленная на рис. 1 модель может быть использована для развития неоптических методов генерации ППП-импульсов и структур [23].

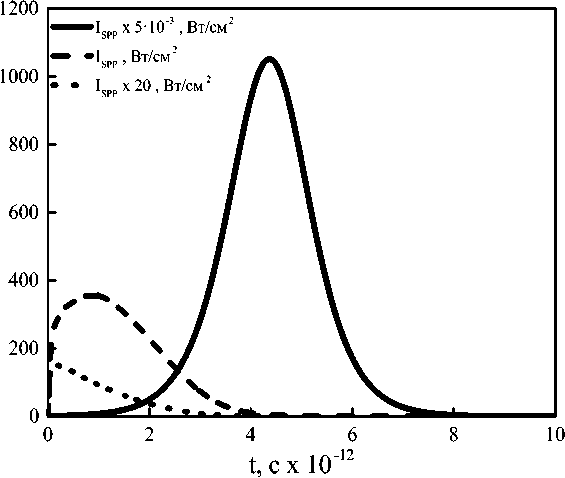
Рис. 2. Профили интенсивности Ispp плазмон-поляритонных возбуждений, формируемых в волноводном спазере, рис. 1 для случаев: 1) малой концентрации КТ N = 10²¹ м^-3, при которой ППП-импульс не успевает сформироваться из-за. сильных диссипативных процессов в металле (пунктирная линия); 2) N = 3 • 10²² м^-3, превышающей пороговую и достаточной для формирования слабого ППП-импульса (штриховая линия); 3) N = 3 • 10²² м^-3 и специальной среды-носителя с подобранным сочетанием параметров пд и п/, при которых Г_е = 0 и происходит формирование интенсивного ППП-импульса (сплошная линия). Параметры взаимодействия: g = 8.33 • 10¹⁰ с^-1, 7_Р = 4.1 • 10¹³ с^-1. Г_а = 6.3 • 10¹¹ с^-1

• 3.    Заключение

В работе с теоретических позиций рассмотрены кооперативные эффекты, возникающие в модели ансамбля полупроводниковых квантовых точек, размещенных в диэлектрической пластине вблизи металлической поверхности. Формирование плазмон-поляритонных импульсов в представленной модели связано с процессом коллективного распада, возбуждений в КТ, аналогично эффекту сверхизлучения в оптике. Однако, в отличие от оптического СИ, энергия коллективных возбуждений конвертируется не в оптический импульс, а обеспечивает ближнеполевую накачку для распространяющихся вдоль границы металл/диэлектрик плазмон-поляритонов. Параметры моделирования, в том числе материал и размер КТ, были выбраны решением задачи оптимизации исходя из условия соответствия частоты межзонного перехода, для КТ и собственных частот формируемых плазмонов. В ходе выполненного моделирования проведено сравнение различных режимов формирования плазмон-поляритонных импульсов на. границе золото/диэлектрик, когда, в качестве накачки используются потупроводниковые оболочечные CdSe/ZnS КТ. Показано, что в условиях сосредоточенной модели и при учете реальных значений скоростей релаксации для КТ и поверхностных плазмон-поляритонов коллективные эффекты обладают конкурентным преимуществом и приводят к формированию субпикосекундных плазмон-поляритонных импульсов при выбранных в работе значениях концентрации КТ.

Техническая реализация описываемых эффектов связана, с необходимостью синтезирования образцов (ансамбль КТ в диэлектрической матрице) с заданными параметрами [24], но может быть осложнена, проблемами временной стабильности отдельных КТ [25].

А. В. Прохоров выражает благодарность А. Б. Евлюхину за. полезные обсуждения. Работа, частично поддержана, грантом РФФИ № 17-42-330029.