Формирование световых полей со сложной поляризационной структурой с использованием астигматической дифракционной линзы

В последнее время возрос интерес к полям с неоднородной поляризацией, в том числе к полям с аксиальносимметричным распределением поляризации. Это, в первую очередь, объясняется особыми свойствами таких полей, которые проявляются при их фокусировке и взаимодействии с веществом. Поля с аксиальносимметричным распределением поляризации используют для исследования свойств отельных молекул [1], для ускорения электронов [2, 3], для обработки, в том числе резки, металлов [4], а также в лазерной манипуляции [5, 6]. Представляется актуальной задача разработки новых способов формирования полей с неоднородной поляризацией. Целью настоящей работы был поиск одного из путей ее решения.

Предложенным ранее общим подходом к формированию пучков с неоднородым распределением поляризации является интерференционное сложение пучков, комплексные амплитуды которых имеют следующий вид [7, 8]:

E 1 (r, 9 ) = ^E ° ⁽r ) ( x m iy )exp( im9 ),

E r 2 ( r , 9 ) = ^E °2 r ) ( x ± iy ) exp(- im9), (1)

где x, y - орты декартовой системы координат, введенной в поперечном сечении пучка, r,9 -цилиндрические координаты. В центре пучка находится особая точка, при обходе вокруг которой по часовой стрелке фаза пучка меняется от 0 до 2 п m раз. В особой точке интенсивность обращается в нуль, а фаза неопределена. Число m также называют топологическим зарядом пучка, а особую точку – сингулярностью. Как видно, данные пучки имеют противоположные по знаку топологические заряды (т.е. комплексно сопряженные фазы), идентичные аксиальносимметричные распределения интенсивности и однородную, но различную по направлению вращения вектора напряженности, круговую поляризацию. В известных экспериментальных схемах для формирования комплексно сопряженных пучков вида (1) используются спиральные фазовые пластинки. Поля, образующиеся при дифракции на таких элементах, не обладают структурной устойчивостью интенсивности и фазы при переходе из ближней в дальнюю зону дифракции [9, 10]. Поэтому интерференционное поле имеет требуемое распределение поляризации только в определенной пространственной области. Пространственно инвариантное распределение поляризации можно получить, используя структурно устойчивые поля вида (1), к которым относятся, в частности, пучки Лагерра-Гаусса:

m r                f К I

^{E (} r ^{, 9 )} = ^E ° I w I exp ^-

r

/

rm

2 ->L 1 2 L l

2 ww

2 A rr w2)

ei m 0

, (2)

где L m ( • ) - полиномы Лагерра-Гаусса, w - по луширина пучка. Для формирования двух ком

-

-

плексно сопряженных пучков Лагерра-Гаусса в данной работе предлагается использовать специ-

альный дифракционный оптический элемент.

2. АСТИГМАТИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ

В работе [11] было показано, что пучки Эрмита-Гаусса H _{n , m} могут быть преобразованы в пучки Лагерра-Гаусса LG _{n , m} путем следующей операции:

JJ exp \ -i (x^+yn )± 2 Цп) HG10 (<^П) d^dn =

R ^{2      V                         7}      ’

= C ^

z^-                 Л \ _ ixy ]

LG I      , —y= I e ^ 4 ⁷ in + 1 order,

0,¹ 1 272 2V2 7

JJ exp f - i ( x ^ + y n ) + 21 ^ ¹ HG n , m Цм ) d ^ d n =

R ^{2 V                     V}

^LG 0, - 1

\           1

( 272 272 J

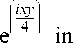
- 1 order.

и + m

= jj ^{(- 1 )} expl

(2i\ m! LG_mn        , |

⁽ )        ^{m,n m} ( 272,272 )

(2 i m n!LG„_m _„ 4=, ^x | ⁽ ) ^n,mn ( 272,272 )

for n >  m ,

for n <  m .

Преобразование (3) названо астигматическим, т.к. в его ядро входит астигматическое слагаемое 2 ^q . Экспериментально такое преобразование удается осуществить с помощью системы сферических и цилиндрических линз (рис. 1).

Оказывается возможным с помощью астигматического преобразования получить комплексно сопряженные пучки Лагерра-Гаусса. Для этого предлагается заменить цилиндрическую линзу, выполняющую астигматическое преобразования пучка Эрмита-Гаусса, на бинарный дифракционный элемент. Фаза такого элемента определяется выражением:

ф = - 0> ₀signcos ( 2 xy + a x ) . (4)

По своей структуре дифракционный элемент представляет собой дифракционную решетку, период которой задается параметром a . При дифракции на данном дифракционном элементе пучка Эрмита-Гаусса в ± 1 порядках дифракции формируются пучки Лагерра-Гаусса. В частном случае [12]:

где C – некоторая постоянная. Фазы пучков Лагерра-Гаусса, как следует из математического представления (5), являются комплексно сопряженными. На рис. 2 представлены результаты численного моделирования.

• 3.    ЭКСПЕРИМЕНТАЛЬНАЯ СХЕМА ФОРМИРОВАНИЯ ПОЛЕЙ С НЕОДНОРОДНОЙ ПОЛЯРИЗАЦИЕЙ

Схема разработанной экспериментальной установки для формирования полей с неоднородной поляризацией на основе дифракционного элемента (4) показана на рис. 3. Гелий-неоновый лазер настроен на генерацию исходного пучка Эрмита-Гаусса с линейной поляризацией. Дифракционный элемент преобразует пучок Эрмита-Гаусса в комплексно сопряженную пару пучков Лагерра-Гаусса. Дополнительные цилиндрические линзы CL1 и CL2 позволяют скомпенсировать остаточный астигматизм exp ( ± xy /4 ) (см. формулу 5). Четвертьволновые пластинки QP1 и QP2 преобразуют линейную поляризацию пучков в левую и правую круговую. С помощью делительного кубика осуществляется интерференционное сложение пучков. Таким образом, на

Рис. 1. Экспериментальная схема астигматического преобразования пучков Эрмита-Гаусса в пучки Лагерра-Гаусса. L - сферическая линза, CL - цилиндрическая линза

Рис. 2. а – фрагмент структуры дифракционного оптического элемента (4); б – картина дифракции на данном дифракционном элементе

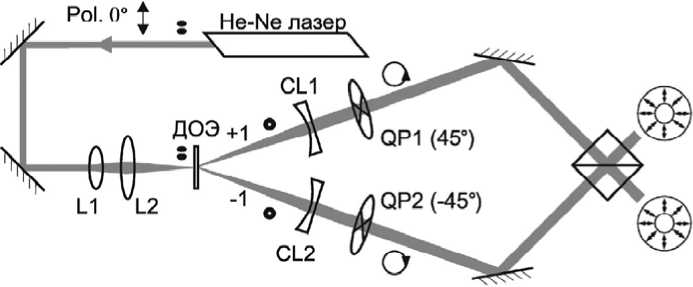
Рис. 3. Схема формирования неоднородно поляризованных пучков на основе дифракционного оптического элемента (ДОЭ)

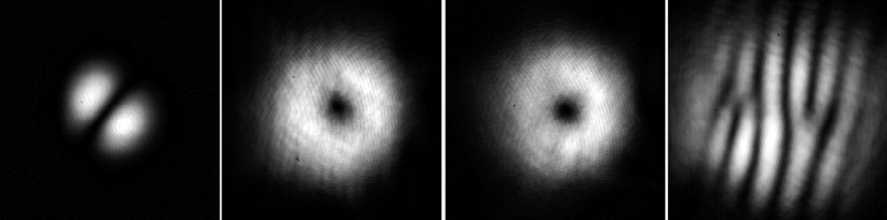
Рис. 4. а – Пучок Эрмита-Гаусса; б, в – пучки Лагерра-Гаусса в ± 1 порядке дифракции, сформированные с помощью дифракционного элемента; г – интерференция пучков Лагерра-Гаусса с противоположными по знаку топологическими зарядами

выходе из системы формируются два идентичных неоднородно поляризованных пучка. Дифракционная эффективность в данном случае составляет порядка 40%, что превышает эффективность ряда известных интерференционных схем более чем в 3 раза.

Дифракционный элемент был изготовлен в Институте систем обработки изображений РАН методом лазерной фотолитографии и химического травления на стеклянной подложке с разрешением 2 мкм. На рис. 4 изображены фотографии исходного пучка Эрмита-Гаусса и пучков Лагерра-Гаусса, полученных с помощью дифракционного элемента. По характерному расположению интерференционных полос на рисунке -4, г можно судить о комплексной сопряженности пучков Лагерра-Гаусса.

• 4.    ЗАКЛЮЧЕНИЕ

В работе представлен дифракционный оптический элемент, осуществляющий преобразование пучка Эрмита-Гаусса в пару комплексно сопряженных пучков Лагерра-Гаусса, что подтверждено результатами эксперимента. На основе данного оптического элемента разработана интерференционная схема формирования пучков с неоднородной поляризацией, которая имеет дифракционную эффективность, более чем в 3 раза превышающую эффективность ряда известных интерференционных схем.

Работа выполнена при поддержке ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009 – 2013 годы (Государственный контракт № 14.740.11.0063) и УНК ФИАН им. П.Н. Лебедева.