Формирование топологической структуры автоматизированной системы управления космическими системами

Современные автоматизированные системы управления (АСУ), в том числе АСУ космических систем, представляют собой сложные системы, характеризующиеся комплексным взаимодействием элементов, рассредоточенных на значительной территории, включая космическое пространство, и требующих для своего развития существенных затрат ресурсов и времени.

Важнейшей проблемой, возникающей при анализе и синтезе подобных систем, является структурное построение системы управления, во многом определяющее свойства системы и характеристики ее функционирования. Разработка структуры системы при создании новых или совершенствовании существующих АСУ космических систем требует решения таких задач, как выбор существующих или создание новых пунктов управления космическими аппаратами, определение топологической структуры системы управления [1].

Однако при формировании структуры АСУ космических систем возникает неопределенность, обусловленная динамикой объекта управления при функционировании системы управления. Эта задача ввиду наличия неопределенности относится к задачам, требующим поддержки принятия решений, при которой информация преобразуется к виду, упрощающему и облегчающему принятие решений.

В информационных технологиях принятием решений считают выбор решений в условиях определенности, позволяющих выбрать однозначные, непротиворечивые, корректные решения на основе формализованных моделей объектов управления и окружающей их среды.

Для решения задачи структурного построения АСУ космической системы необходимо создание модельно-алгоритмических средств выбора пунктов управления космическими аппаратами, что требует разработки имитационных процедур принятия решений при формировании системы управления космической системы.

Топологическая структура АСУ космической системы определяет взаимное расположение и количест- во пунктов управления (ПУ) для заданных классов космических аппаратов (КА) [2]. Задача формирования топологической структуры комплекса ПУ КА заключается в следующем: для заданных множеств КА различных классов EКА, множества участков возможной доступности L, графика движения Gk и программы работ Пk КА каждого класса необходимо найти минимальную по затратам на создание совокупность ПУ, чтобы при этом выполнялись требования к управляемости и коэффициенту доступности для заданных классов КА, загрузке ПУ, специальные требования к системе (например, доступность на одном витке КА не менее чем для двух ПУ, минимально допустимое время нахождения КА в зоне какого-либо ПУ и т. д.). В результате решения данной задачи определяется, какие ПУ необходимы в системе и с какими классами КА они будут взаимодействовать.

Для формализации задачи формирования топологической структуры АСУ космической системы дополнительно введем следующие обозначения: θkl – время доступности КА k-го класса на l-м участке возможной доступности; cj – затраты на создание j-го ПУ; τk min – минимально допустимая продолжительность одного сеанса связи для КА k-го класса; Rk – минимальное число ПУ, необходимых для управления КА k-го класса; Lμk – множество смежных участков доступности из Lk с непрерывным временем доступности для КА k-го класса; Hk – коэффициент доступности КА k-го класса, который определяется отношением общего времени доступности КА к -го класса т к = ^ т kj ко времени нахождения КА j ' Jk k-го класса над заданной территорией.

Введем переменные:

Г 1, если в системе будет использован j -й ПУ;

Zj = 1

[ 0, в противном случае;

[ 1, если в системе будет использован yt = 11-й участок возможной доступности;

[ 0, в противном случае.

Модель формирования топологической структуры системы имеет вид

Z c j z j ^ min              (1)

j eJ при следующих ограничениях:

– на коэффициент доступности для каждого класса КА:

Z0Hyi I тk > Hk; k e K;(2)

^{l e} Lk

– на минимальное количество ПУ, необходимых для управления каждым классом КА:

Z Zj> Rk, k e K;

j e J

– на минимальную продолжительность сеанса связи для КА k -го класса:

Z 0k/У/ > тkmm;

^{l e} L v k

– на связь между переменными:

Z z/> yi >(11 \Ji I) Z zj, 1 e L.

j e Ji                          j e Ji

Аналитическая часть задачи формирования, определяемая выражениями (1)–(5), представляет собой линейную целочисленную модель математического программирования, и варианты структуры АСУ космической системы могут быть получены с помощью известных методов [3]. Выражения (2)–(5) задают множество аналитически заданных ограничений β′. Множество алгоритмически заданных ограничений β″ задается при ограничениях на управляемость каждого класса КА и на загрузку пунктов управления. При проверке на допустимость по алгоритмически заданным атрибутам в качестве параметров имитационной модели выступают вариант комплекса ПУ КА X i , программы работ КА каждого класса П _k , объем информации, передаваемый за время осуществления управляющего взаимодействия между КА k -го класса и ПУ ξ _kn , N_k – количество КА k -го класса, график движения КА k -го класса G_k .

Для решения задачи синтеза топологической структуры комплекса наземных пунктов управления АСУ космической системы, содержащей аналитически и алгоритмически заданные ограничения, разработана и программно реализована процедура, которая заключается в направленном переборе множества вариантов структуры, использующем схему «ветвей и границ» [4], и последующей проверке их принадлежности множеству β′, осуществляемой с помощью имитационной модели.

Процесс поиска оптимального варианта структуры opt

АСУ космической системы X можно представить в виде дерева вариантов, в котором нулевая вершина соответствует оптимальному решению X0 , а каждая из вершин, связанных с ней ребрами, соответствует другому ее решению при дополнительном условии, что переменной xkm,n придано конкретное значение xm” ={0,1}.

Каждой из вершин дерева соответствует оценка Y m ^- ” , равная оптимальному значению целевой функции для соответствующей задачи. Необходимость в дальнейшем ветвлении вершины возникает в случае невыполнения условий целочисленности, при этом на следующем шаге ветвления выбирается вершина с наименьшей оценкой.

Каждая конечная вершина дерева соответствует варианту структуры АСУ космической системы Xk ев', который с помощью имитационной модели проверяется на выполнение алгоритмически заданных ограничений. Процесс продолжается до тех пор, пока дальнейшее ветвление становится невозможным. Оп-opt тимальный вариант структуры X соответствует конечной вершине, удовлетворяющей алгоритмически заданным ограничениям и имеющей наименьшую оценку Ymin .

Для данной процедуры характерны следующие особенности.

• 1.    Разбиение множеств (ветвление). Правило выбора переменной для дальнейшего ветвления состоит в следующем. Для каждой из переменных

• 2.    Вычисление оценок (нижних границ). Для начального множества P ₀ оценка значения целевой функции снизу y ( P ₀) = f ( X ₀), где X ₀ — оптимальное решение оценочной задачи линейного программирования. Для множества в mm оценка y ( P mm ) = f ( X ^m ), где X_n^m – оптимальное решение оценочной задачи, X m ев m , y ( p m ) =« .

m xk- e X” I k = 1,K” ), принявших нецелочисленное значение, вычисляются значения целевой функции f> (Xm0) и f1 (X”mi) соответственно при значениях xkm,n = 0 и xkm,n = 1. Для дальнейшего разбиения выбирается переменная, которая обеспечивает наибольшую абсолютную разность между полученными значениями целевой функции, т. е.

max {Akm” = (fx (X%:л) - f > (X%m0)(k = iKm}, и ей присваивается значение, дающее наименьшее возрастание целевой функции.

Рассмотрим пример формирования АСУ космической системы, которая включает совокупность наземных пунктов управления, осуществляющих управление КА трех классов Е _КА = { Е К _А I k = 1,3 } , имеющих геосинхронные орбиты с постоянными периодами обращения.

Задана следующая исходная информация: множество возможных ПУ ЕПу = {ej I j = 1,9}; затраты на создание j-го ПУ; множество участков возможной доступности и время доступности КА k-го класса на l-м участке θkl (табл. 1); количество КА каждого класса Nk (k = 1,3) и множество возможных ПУ для каждого класса КА mk (к = 1,3); продолжительность доступ -ности КА k-го класса j-му возможному ПУ тk(к = 13, j = 19) (табл. 2).

График движения k -го класса, учитывающийся в имитационной модели, определяется массивами, элементы которых определяют соответственно порядок прохода КА через зоны доступности ПУ, продолжительность нахождения КА в зонах доступности каждого ПУ и нахождения вне зон доступности при переходе от одного ПУ к другому, если между зонами доступности соседних ПУ нет разрыва (табл. 3).

Программа работ КА к -го класса Пк (к = 1,3) задается периодичностью осуществления управляющего взаимодействия n-го типа, его продолжительностью и приоритетом. Рассматриваются два типа управляющих взаимодействий. Управляющее взаимодействие 1-го типа имеет 1-й приоритет, время его осуществления является случайной величиной с нормальным законом распределения и математическим ожиданием, равным 3,5 мин, стандартным отклонением 0,4 мин, максимальным значением 5 мин, минимальным значением 2 мин. Управляющее взаимодействие 2-го типа имеет 2-й приоритет, продолжительность которого также нормально распределена с математическим ожиданием, равным 2 мин, стандартным отклонением 0,25 мин, максимальным значением 3 мин, минималь- ным значением 1 мин. Периодичность осуществления управляющих взаимодействий n-го типа для КА всех классов приведена в табл. 4.

Кроме того, заданы ограничения на глобальность

Нк (к = 1,3), минимальное количество пунктов управления, необходимых для управления КА k-го класса Мк (к = 1,3), ность управляющего класса Тkmin (к =1,3)

минимальную продолжитель-взаимодействия для КА k -го

и на управляемость каждого

класса КА ю до ( к = 1,3 ) (табл. 5), а также заданы ограничения на загрузку каждого ПУ U j ™ ( j = 1,9 ) .

Оптимальный вариант топологической структуры рассматриваемой АСУ космической системы, полученный с помощью имитационной процедуры, приведен в табл. 6, где показан оптимальный состав пунктов управления и используемые участки доступности. Общая стоимость создания варианта составила 15 усл. ед.

Решение задач исследования устойчивости полученного оптимального варианта топологической структуры АСУ космической системы позволило определить потенциальные возможности развития системы без изменения ее структуры и при выполнении требований к качеству ее функционирования.

В частности, решалась задача определения возможности одновременного увеличения числа КА 1-го класса и продолжительности управляющих взаимодействий 1-го типа при выполнении требований к управляемости КА и загрузке ПУ.

Таблица 1

Время доступности космических аппаратов на участках возможной доступности, мин

Класс КА	Участки возможной доступности L k
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	6	2,0	5	2,5	7,5	5	7	–	–	–	–	–	–	–	–	–	–	–
2	–	–	–	–	–	–	–	9	3	5	6	1	9	–	–	–	–	–
3	–	–	–	–	–	–	–	–	–	–	–	–	–	6,5	1,5	6	1,5	5,5

Таблица 2

Продолжительность нахождения космических аппаратов в зонах доступности, мин

Класс КА	Пункты управления
	1	2	3	4	5	6	7	8	9
1	8	–	10	–	5	7	9	–	–
2	–	12	6	9	–	–	–	–	7
3	–	–	–	8	7	–	–	9	–

Таблица 3

Данные по графикам движения различных классов космических аппаратов

Порядок прохождения КА k -го класса по пунктам управления			Продолжительность нахождения в зонах доступности, мин			Продолжительность нахождения вне зон доступности, мин
k = 1	k = 2	k = 3	k = 1	k = 2	k = 3	k = 1	k = 2	k = 3
2	4	6	8	12	8	0	0	0
7	9	8	10	7	9	0	1	0
3	3	5	10	6	7	0	6	0
5	4	0	5	9	0	0,5	10	155
6	0	0	7	0	0	121	0	0

Таблица 4

Периодичность осуществления управляющих взаимодействий

Класс КА	Тип управляющих взаимодействий
	1-й	2-й
1	3	5
2	3	7
3	4	5

Таблица 5

Ограничения на классы космических аппаратов

Класс КА	Ограничения
	H k	M k	τ k min , мин	® kon
1	0,7	4	2	0,95
2	0,8	2	1	0,8
3	0,7	2	1	0,8

Таблица 6

Оптимальный вариант топологической структуры АСУ космической системы

Класс КА	Участки возможной доступности L k	Пункты управления
1	{P 1 , P 2 , P 4 , P 5 , P 6 , P 7 }	{ПУ1, ПУ3, ПУ5, ПУ6}
2	{P 8 , P 11 , P 13 }	{ПУ2, ПУ3, ПУ4}
3	{P 14 , P 17 , P 18 }	{ПУ4, ПУ5}

Для решения данной задачи исследовались два функциональных параметра: N 1 – количество КА 1-го класса и Т 1 – средняя продолжительность управляющих взаимодействий 1-го типа, а качество функционирования системы оценивалось по управляемости КА 1-го класса ю , и загрузке ПУ U j ( j = 1,3 ) . В качестве интервалов возможных значений исследуемых параметров были выбраны L 1 = [ N ®³³ , N mx ] = [ 30; 45 ] и L 2 = [ T_v⁶” , T max ] = [ 3,5; 6,5 ] .

Базовые значения функциональных параметров N1баз и T1баз , т. е. значения, которые использовались в качестве исходных данных при формировании исследуемого варианта структуры, соответственно равны 30 и 6,5. Результаты исследования приведены в табл. 7.

Таким образом, в результате исследования устойчивости структуры было определено, что автоматизированные системы управления космической системы с данным вариантом топологической структуры обладает потенциальными возможностями дальнейшего развития без дополнительных затрат.

Число КА 1-го класса может быть увеличено с 30 до 45 и средняя продолжительность управляющих взаимодействий 1-го типа – с 3,5 до 5,1 мин при выполнении требований к качеству функционирования системы.

Рассмотрим другой пример формирования структуры АСУ космической системы. Допустим, что разрабатывается топологическая структура АСУ космической системы для управления тремя классами космических аппаратов (см. рисунок).

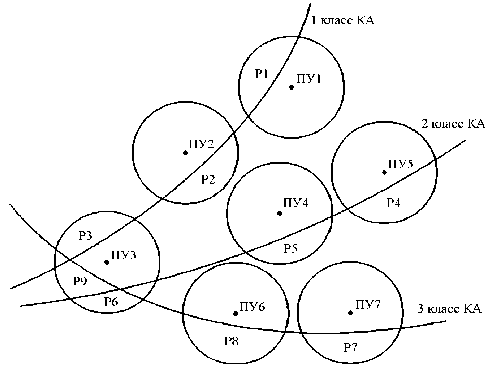
Зоны доступности и траектории полета космических аппаратов

Исходные данные: количество ПУ – 7, количество классов КА – 3, количество участков доступности – 9 (табл. 8–10).

Таблица 7

Результаты исследования устойчивости топологической структуры АСУ космической системы

Параметры и характеристики	Номер эксперимента
	1	2	3	4	5
N 1	45	37	41	39	38
T 1 , мин	6,5	4,9	5,7	5,3	5,1
® 1	0,843	0,975	0,880	0,970	0,960
U 1	0,710	0,470	0,600	0,485	0,775
U 2	0,670	0,550	0,550	0,570	0,560
U 3	0,720	0,480	0,550	0,510	0,490

Таблица 8

Время доступности космических аппаратов на участках возможной доступности

Класс КА	Участки возможной доступности
	1	2	3	4	5	6	7	8	9
1	10	5	6	–	–	–	–	–	–
2	–	–	–	5	6	5	–	–	–
3	–	–	–	–	–	–	3	4	4

Таблица 9

Ограничения и полное время полета над территорией

Класс КА	N k	M k	τ k min , мин	Полное время полета τ k , мин
1	0,6	1	9	15
2	0,7	2	10	12
3	0,6	3	9	14

Таблица 10

Стоимость построения пунктов управления

Порядковый номер, ПУ	1	2	3	4	5	6	7
Стоимость, усл. ед.	30	50	40	45	50	55	35

Результаты решения задачи сведены в таблицу (табл. 11).

Стоимость полученного комплекса пунктов управления, входящих в состав автоматизированной системы управления космической системы, составляет 205 усл. ед., что на 100 усл. ед. меньше стоимости исходного комплекса.

Таблица 11

Оптимальный вариант топологической структуры АСУ космической системы

Класс КА	Участки доступности L k	Пункты управления m k
1	1, 3	1, 3
2	5, 6	3, 4
3	7, 8, 9	3, 6, 7

В работе получил развитие имитационный подход к формированию автоматизированных систем управления космическими системами, предназначенный для выбора оптимального комплекса пунктов управления и топологии системы.

Разработанный модельно-алгоритмический аппарат позволяет автоматизировать процесс выбора пунктов управления космическими аппаратами, определяя их минимально необходимое количество и рациональное распределение в пространстве. Метод выбора топологической структуры АСУ космической системы имеет важное значение для решения широкого спектра практических задач формирования структур сложных систем управления.