Формирование управленческих решений с помощью метода обратных вычислений в условиях определенности

Обратные вычисления относятся к трудным задачам, так как в общем случае они являются некорректно поставленными задачами, наиболее часто нарушается свойство устойчивости: метод нахождения решений при одних исходных данных не всегда даст решение при изменении начальных условий.

Как известно, решения могут приниматься в условиях определенности, неопределенности и риска. «Под определенностью будем понимать ситуацию, когда каждой альтернативе решения соответствует известный набор последствий. Это значит, что задача хорошо формализована (есть модель решения); существует критерий оценки качества решения; последствия решения известны» (Одинцов Б.Е. Обратные вычисления в формировании экономических решений. М., 2004.).

Итак, суть обратных вычислений состоит в том, что для функции двух аргументов находятся приращения аргументов, обеспечивающие заданное приращение функции без построения обратной зависимости. Решение обратных задач можно прово- дить разными методами: можно учитывать или нет приоритетности целей, можно применять единый коэффициент прироста, а можно задавать разные значения коэффициентов, можно вообще обойтись без коэффициентов. Выбор метода определяется видом функции или поставленной целью.

Рассмотрим применение метода обратных вычислений для формирования управленческих решений в экономической задаче, который учитывает приоритет целей и единый коэффициент прироста.

Постановка задачи. На предприятии в течение нескольких отчетных периодов прибыль от продаж была значительно ниже запланированных показателей, что не позволяло развивать производство. Руководство предприятия приняло решение о повышении прибыли от продаж до 3600 ед. за счет роста выручки от продаж и снижения себестоимости путем увеличения объема выпуска продукции, снижения цены единицы продукции и снижения совокупных переменных расходов и постоянных затрат.

На текущий момент определены показатели: объем выпуска продукции – 100 ед. по цене 100 у.е. за единицу, при этом постоянные затраты составляют 3000 у.е. и величина совокупных переменных расходов равна 4000 у.е.

Прибыль от продаж получается за счет разницы между выручкой и себестоимостью произведенных продуктов:

ПП = В – С, где ПП – прибыль от продаж за месяц; В – выручка от продаж; С – себестоимость продукции за месяц;

В = К · Ц, где К – объем выпуска продукции, шт.; Ц – цена единицы продукции, у.е.;

С = ПЕР + ПОСТ, где ПЕР – совокупные переменные расходы, у.е. за месяц; ПОСТ – постоянные затраты, у.е. за месяц.

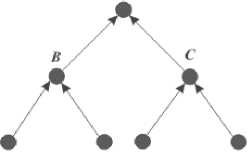
• 1    шаг. Прямая задача. Рассчитаем фактическое значение прибыли от продаж за месяц, т.е. решим прямую задачу, дерево которой представлено на рисунке 1.

пи

К       Ц ПЕР ПОСТ

Рис. 1. Дерево прямой задачи

По условию задачи известны значения: К = 100 ед. продукции, Ц = 100 у.е. за единицу, ПОСТ = 3000 у.е., ПЕР = 4000 у.е.

По расчетным формулам вычислим значения на текущий момент:

• -    себестоимость продукции за месяц: С = ПЕР + ПОСТ = 4000 + 3000 = 7000 у.е.;

• -    выручка от продаж: В = К · Ц = 100 · 100 = 10000 у.е.;

• -    прибыль от продаж за месяц: ПП = В – C = 10000 – 7000 = 3000 у.е.

Таким образом, чтобы достичь запланированного уровня прибыли от продаж ПП = 3600, надо увеличить прибыль на величину ∆ ПП = 3600 – 3000 = 600.

• 2 шаг. Обратная задача. Обратная задача заключается в определении величины приращений показателей К , Ц , ПОСТ , ПЕР , обеспечивающих увеличение прибыли на величину ∆ ПП = 600.

Для проведения обратных вычислений, учитывающих решение руководства о путях повышения прибыли, дополним расчетные формулы целевыми установками: знак показывает, за счет уменьшения или увеличения показателя достигается цель, а коэффициенты относительной важности аргументов α_i и β_i ( α_i + β_i = 1) определяют приоритеты в достижении цели.

Дерево целей обратной задачи представлено на рисунке 2.

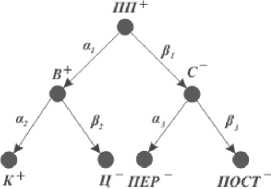
Рис. 2. Дерево целей обратной задачи

Согласно дереву целей для решения поставленной задачи необходимо решить несколько обратных задач.

Задача 1. Для решения задачи воспользуемся расчетной формулой: ПП = В – C .

Определим изменения выручки и себестоимости, которые обеспечат увеличение прибыли от продаж на величину ∆ ПП = 600. Отметим, что по решению руководства увеличение прибыли от продаж необходимо получить в большей степени за счет увеличения выручки ( В ⁺), чем за счет снижения себестоимости ( С ^–). Это дает возможность построить целевую установку задачи: ПП ⁺ = В + ( α ₁) – С ^–( β ₁), где коэффициенты относительной важности аргументов α ₁ = 0,6 и β ₁ = 0,4 ( α ₁ >  β ₁) устанавливают, что часть прироста прибыли от продаж, равная 0,6, должна быть обеспечена за счет увеличения выручки, а другая часть, равная 0,4, – за счет уменьшения себестоимости.

При применении единого коэффициента k ₁ одновременно с коэффициентом относительной важности каждого аргумента прирост каждого аргумента представляется следующим образом:

∆ В = α ₁ k ₁, ∆ С = β ₁ k ₁.

Заметим, что должны выполняться условия: α ₁ + β ₁ = 1 и k ₁ > 0.

Задача обратных вычислений примет вид: ПП + ∆ПП = (В + ∆В) – (С – ∆С), или ПП + ∆ПП = (В + α1k1) – (С – β1k1).

Решив полученное уравнение относительно k ₁, найдем: k ₁ = ∆ ПП . Затем вычислим ∆ В , ∆ С и новые значения В + ∆ В , С – ∆ С .

Результаты вычислений в Excel представлены в таблице 1:

Таблица 1

	A	B	C	D	E
2 3	Наименование показателя	Обозначения	исходное	Значения расчетное (желаемое)	Приращение
4	Выручка	В	10000	10360	360
5	Стоимость товаров	С	7000	6760	240
6	Прибыль от продаж	ПП	3000	3600	600
7	–	α 1 =	0,6	–	–
8	–	β 1 =	0,4	–	–
9	–	k 1 =	600	–	–

Расчетные значения выручки, себестоимости и прибыли

Сделаем проверку вычислений:

ПП + ∆ ПП = 10360 – 6760 = 3600.

Таким образом, расчетные значения выручки, себестоимости и их приращений составят соответственно:

∆ В = 360, В + ∆ В = 10360, ∆ С = 240, С – ∆ C = 6760.

Задача 2. В результате решения задачи 1 определили, что для достижения конечной цели – увеличения прибыли от продаж ( ПП ) – следует увеличить выручку ( В ) на ∆ В = 360 у.е. Во второй задаче необходимо определить величину приращений аргументов, формирующих выручку.

Зависимость выручки ( В ) от цены ( Ц ) и объема произведенной продукции ( К ) задается выражением: В = К · Ц .

Целевая установка может быть записана следующим образом: В + = К + ( а 2 ) • Ц"(в 2 ).

Зададим значения коэффициентов относительной важности аргументов: α ₂ = 0,7 и β ₂ = 0,3 ( α ₂ >  β ₂, так как увеличение выручки планируется получить в большей степени за счет увеличения объема продаж, чем за счет снижения цены продукта). Введем единый коэффициент k ₂ и запишем искомые приращения ∆ К = α ₂ k ₂, ∆ Ц = β ₂ k ₂.

Задача обратных вычислений заключается в поиске величины из уравнения:

В + ∆ В = ( К + ∆ К ) · ( Ц – ∆ Ц ), или В + ∆ В = ( К + α ₂ k ₂) · ( Ц – β ₂ k ₂).

После преобразований получим квадратное уравнение относительно k ₂:

α2β2k22 – k2(α2Ц – β2К) + ∆В = 0, решив которое получим формулу для вычисления коэффициента:

α ₂ Ц – β ₂ К ± √ ( α ₂ Ц – β ₂ К )² – 4 α ₂ β ₂ ∆ В k =                                 =

²                      2 α ₂ β ₂

0,7 · 100 – 0,3 · 100 ± √ (0,7 · 100 – 0,3 · 100)²– 4· 0,7 · 0,3 · 360   40 ± √ 1297,6   40 ± 36,02

2 · 0,7 · 0,3

0,4 · 2           0,4 · 2

Из формулы видно, что в этой задаче коэф- фициент k2 может принимать два значения. Выбор одного из них проводится либо с помощью усло- вия k2 > 0, либо исходя из экономического смысла.

Вычислим оба значения k ₂:

40 + 36,02

к' =---------- = 181,01; к"

2       0,42                 2

40 – 36,02

= 9,47.

0,42

Оба значения неотрицательны, следовательно, выбрать одно из них следует, ориентируясь на экономический (здравый) смысл.

Вычислим приращения аргументов при значении k ₂ = 181,01:

∆ К = α ₂ k ₂ = 0,7 · 181,01 = 126,70;

∆ Ц = β ₂ k ₂ = 0,3 · 181,01 = 54,3.

Получается, что для того чтобы получить заданное приращение ∆В = 360 у.е., надо увели- чить количество продуктов (К) на величину ∆К = 126,70, т.е. более чем в два раза, а цену за единицу (Ц) продукта снизить на величину ∆Ц = 54,3, т.е. тоже почти в два раза. Очевидно, что такое управленческое решение неразумно. Поэтому из двух возможных значений коэффициента k2 выберем значение k2 = 9,47 и проведем аналогичные расчеты (см. табл. 2).

Сделаем проверку вычислений:

В = К · Ц = 106,63 · 97,16 = 10360.

Таким образом, для решения поставленной задачи следует увеличить количество продуктов на величину ∆ К = 6,36 и снизить цену за единицу продукта на величину ∆ Ц = 2,84. При этом произвести продукта надо в количестве К = 106,63 и установить цену за одну единицу Ц = 97,16 у.е.

Таблица 2

Расчетные значения объема продукции, цены и выручки

	A	B	C	D	E
12 13	Наименование показателя	Обозначения	исходное	Значения расчетное (желаемое)	Приращение
14	Объем продукции	К	100	106,63	6,63
15	Цена	Ц	100	97,16	2,84
16	Выручка	В	10000	10360	360
17	–	α 2 =	0,7	–	–
18	–	β 2 =	0,3	–	–
19	–	k 2 =	9,47	–	–

Задача 3. В ходе решения задачи 1 определили, что для увеличения прибыли от продаж ( ПП ) на 600 ед. себестоимость продукта ( С ) надо уменьшить на ∆ С = 240 у.е. Руководство предприятия решило добиться такого изменения за счет снижения совокупных переменных расходов ( ПЕР ) и постоянных затрат ( ПОСТ ). При этом большая часть изменения себестоимости продукта должна быть обеспечена уменьшением переменных расходов.

Исходя из этого целевую установку построим на основе известной зависимости себестоимости продукта от совокупных переменных расходов и постоянных затрат:

С ^– = ПЕР ^– ( α ₃) + ПОСТ ^– ( β ₃),

Таблица 3

Расчетные значения показателей задачи 3

	A	B	C	D	E
21	Наименование показателя	Обозначения	Значения		Приращение
22			исходное	расчетное (желаемое)
23	Переменные расходы	ПЕР	4000	3820	180
24	Постоянные затраты	ПОСТ	3000	2940	60
25	Себестоимость товаров	С	7000	6760	240
26	–	α 3 =	0,75	–	–
27	–	β 3 =	0,25	–	–
28	–	k 3 =	240,0	–	–

Таким образом, решив серию обратных задач, определили, что для выполнения решения руководства о повышении прибыли от продаж до 3600 у.е. надо организовать мероприятия, обеспечивающие: увеличение объема выпуска продукции на 6,63 ед., снижение цены единицы продукции на 2,84 у.е. и снижение совокупных переменных расходов и постоянных затрат соответственно на 180 у.е. и 60 у.е. При этом выручка от продаж увеличится на 360 у.е., а себестоимость снизится на 240 у.е.

Рассмотрим другие методы обратных вычислений, решив одну задачу разными методами, и проведем сравнение полученных результатов.

Задача 4. Решим задачу 1 без указания коэффициентов относительной важности: определим изменения выручки ( В ) и себестоимости ( С ), которые обеспечат увеличение прибыли от продаж на величину ∆ ПП = 600 при условии, что изменения этих величин должны быть пропорциональны одному и тому же коэффициенту (приоритет изменений уже не учитывается).

Целевая установка и дерево этой задачи останется без изменений:

ПП ⁺ = В ⁺ – С ^– .

Введем единый коэффициент k0, который учитывает целевую установку следующим об- где коэффициенты относительной важности аргументов заданы: α3 = 0,75 и β3и= 0,25 (α3 > β3).

Введем единый коэффициент k ₃, с помощью которого определяются искомые приращения аргументов: ∆ ПЕР = α ₃ k ₃, ∆ ПОСТ = β ₃ k ₃.

Задача обратных вычислений заключается в поиске величины k ₃ из уравнения

С – ∆C = (ПЕР – ∆ПЕР) + (ПОСТ – ∆ПОСТ), или С – ∆C = (ПЕР – α3k3) + (ПОСТ – β3k3).

Выразив из полученного уравнения k3, по- лучим:

k = ^{∆ C}   .

³ α ₃ + β ₃

Результаты вычислений по задаче 3 приведены в таблице 3.

разом: аргумент В увеличивается; В + ∆ В = k ₀ В ; аргумент С уменьшается: С – ∆ С = С / k ₀.

Задача сводится к решению уравнения с одним неизвестным k ₀. Тогда задача обратных вычислений примет вид:

ПП + ∆ ПП = ( В + ∆ В ) – ( С – ∆ С ), или ПП + ∆ ПП = k ₀ В – С / k ₀ при условии k ₀ > 1. Для нахождения решим квадратное уравнение: k ₀ ² В – k ₀( ПП + ∆ ПП ) – С = 0 →

( ПП + ∆ ПП ) ± √ ( ПП + ∆ ПП )²+ 4 ВС

Вычислим значения коэффициента:

3600 ± √ 3600²+ 4 ·10000 · 7000

=             2 · 10000

3600 ± 17116,074

=       20000

Из формулы видно, что в этой задаче коэффициент k ₀ может принимать два значения:

3600 + 17116,074 k´=

3600 – 17116,074 k"=

1,0358,

≈ –0,68.

По условию k ₀ > 1, поэтому корень k ^"₀ ≈ –0,68 является посторонним. Найдем приращения аргу-

ментов со значением k ₀ = 1,0358. Результаты представлены в таблице 4.

Расчетные значения показателей задачи 4

Таблица 4

	A	B	C	D	E
1	Наименование показателя	Обозначения	Значения		Приращение
2			исходное	расчетное (желаемое)
3	Выручка	В	10000	10358,04	358,04
4	Стоимость товаров	С	7000	6758,04	242
5	Прибыль от продаж	ПП	3000	3600	600
6	–	k 0 =	1,0358	–	–

∆ В  α

Сделаем проверку вычислений:

ПП + ∆ ПП = 10358 – 6758 = 3600.

Таким образом, расчетные значения выручки, себестоимости и их приращений составят соответственно: ∆ В = 358, В + ∆ В = 10358, ∆ С = 242, С – ∆ C = 6758.

Задача 5. Теперь посмотрим, как изменятся значения выручки ( В ) и себестоимости ( С ) при условии, что изменения этих величин должны быть пропорциональны индивидуальным коэффициентам и учитывать пожелания руководства.

Целевая установка этой задачи: ПП ⁺ = В ⁺( α ₄) – С ^– ( β ₄).

Введем индивидуальные коэффициенты и выразим приращения:

В + ∆ В = k ₄ В → ∆ В = k ₄ В – В ;

С – ∆ С = С / k ₅ → ∆ С = С – С / k ₅.

Тогда целевая функция примет вид:

ПП + ∆ ПП = ( В + ∆ В ) – ( С – ∆ С ), или ПП + ∆ ПП = k ₄ В – С / k ₅ при условии k _{4, 5} > 1.

Изменение прироста аргументов прямой функции пропорционально долям и определяется отношением:

∆ С β

Задачу обратных вычислений запишем как систему уравнений:

¹ ПП + ∆ ПП = ( В + ∆ В ) – ( С – ∆ С ) ∆ В  α

_{∆ С} = _β

ПП + ∆ ПП = k ₄ В – С / k ₅

k ₄ В – В

_{С – С / k 5}

α

β

.

Решив систему относительно k ₄ и k ₅, получим:

k 4 =

k 5 =

α (C + ПП + ∆ ПП ) + βВ

В С

.

k ₄ В – (C + ПП + ∆ ПП )

Решение этой задачи имеет следующие результаты (см. табл. 5).

Сравним полученные результаты со значениями, найденными в задачах 1, 4 и 5 (см. табл. 6). Как видим, результаты отличаются не существенно, а иногда разные методы дают одинаковый результат. На практике часто встречаются ситуации, когда один из методов невозможно применить.

Таблица 5

Расчетные значения показателей задачи 5

	A	B	C	D	E
11	Наименование показателя	Обозначения	Значения		Приращение
12			исходное	расчетное (желаемое)
13	Выручка	В	10000	10360	360,0
14	Стоимость товаров	С	7000	6760	240
15	Прибыль от продаж	ПП	3000	3600	600
16	–	α =	0,6	–	–
17	–	β =	0,4	–	–
18	–	k 4 =	1,036	–	–
19	–	k 5 =	1,036	–	–

Таблица 6

Приращения	Единый коэффициент без указания приоритетности	Единый коэффициент с указанием приоритетности	Разные коэффициенты с указанием приоритетности
∆В	358,04	360	360
∆С	242	240	240

Сравнительная характеристика

К преимуществам метода обратных вычислений для решения обратных задач с экономическим содержанием можно отнести: доказательность, отсутствие сложного математического аппарата, возможность использования электрон- ных таблиц со всем спектром автоматизаций вычислений. Достижение поставленной цели возможно несколькими способами, что дает возможно сть выбрать приемлемый вариант решения.