Формирование волновых фронтов в градиентных волноводах с изгибами малых радиусов

ФОРМИРОВАНИЕ ВОЛНОВЫХ ФРОНТОВ В ГРАДИЕНТНЫХ ВОЛНОВОДАХ С ИЗГИБАМИ МАЛЫХ РАДИУСОВ

Повышение интереса к исследованиям распространения света в изогнутых световодах обусловлено развитием волоконно-оптических линий связи и интегральной оптики.

На практике имеются не только прямые волноводы, во многих случаях они бывают изогнутыми, что приводит к трансформации энергии между модами. Перераспределение энергии между направляемыми модами влияет на межмодовую дисперсию и приводит к искажению передаваемого сигнала, а переход же энергии в моды излучения ведет к потерям.

Изогнутые световоды рассматривались в основном с целью изучения потерь на изгибах [1-4]. Анализ влияния малых отклонений оси градиентного волокна от прямой линии на связь между его модами приведен в [5].

Целью настоящей работы является исследование связи между модами многомодового световода с параболическим профилем показателя преломления при искривлении его оси по некоторому радиусу г.

Эффективный профиль показателя преломления

Рассмотрим плоский световод с параболическим профилем показателя преломления:

п2(х) = п2 - о2х2           1x1 < а п2(х) = п2 - щ2а2 = п2 1x1 > а

В [1] показано, что если световод (1) изогнут по радиусу г, то для исследования распространения света в нем можно рассматривать эквивалентный прямолинейный световод с эффективным профилем показателя преломления п2 (х) = n2(x) (1 + £)2 ,                                               (2)

эфф                  г который удовлетворяет тому условию, что распределения поперечного поля в нем и в изогнутом световоде совпадают. На рис. 1 представлены профиль показателя преломления (1) и эффективный профиль показателя преломления (2), который удобно записать в виде

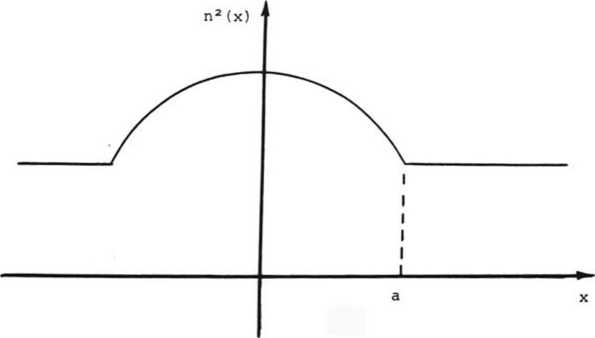
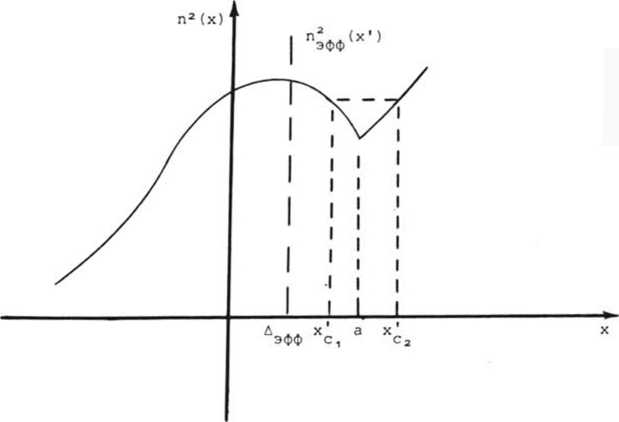
Рис. 1

пэфф<х'> =^2- “'2x'2 "< 1 + ^ 1 * 8 ^ > £ х'3 ~

- ^ х'“ ,   1x1 < а                                                     (3)

г х' ~

ПЭФФ(Х') ^ + ----7^Ф   1x1 > а/ где:

х 1 = х + д * эфф

ДЭФФ = 7 1 + 8 377г :

по = п(Д ) (1 + ^^) ; эфф          Г '                               ___________

- юз-

Отсюда видно, что распространяющееся по волноводу излучение при искривлении его оси смещается к внешней границе волновода, причем вели чина смещения определяется значением дэфф(г)* п₽и уменьшении радиуса изгиба глубина эффективного профиля показателя преломления уменьшается, что вызывает переход высших направляемых мод в моды излучения. При не котором критическом радиусе

кр

на rRp была оценена в работе [з]

все излучение покинет волновод. Величи-. Очевидно, что это соответствует случаю,

когда Дэфф(г)

становится равным полуширине волновода а.

При lx'I < а - Дэфф = аэфф

(1 +   1 + 8       ) -2 х' 3 + — х' * « 1

и2 г2 гг и эффективный профиль показателя преломления эквивалентного прямолинейного световода в первом приближении можно аппроксимировать параболичным п2,(х1) = п'2 - ш'2 х'2 .(6)

эффо

Таким образом, исследование распространения света в изгибах световодов с параболическим профилем показателя преломления сводится к аналогичной задаче для несоосной стыковки волноводов с различными градиентными параметрами, которая была рассмотрена в работах [б, 7].

Известно, что в параксиальном приближении при параболическом поперечном распределении показателя преломления частота осцилляции траектории луча не зависит от его амплитуды и одинакова для всех лучей [5,8]. То есть ячейк а фазового пространства координат и импульсов, соответствующая входному пучку, перемещается без деформации границ. Для такого волновода на расстояниях, кратных периоду осцилляции траектории луча, распределение поперечного поля будет повторять начальное. Однако при учете непараксиальности, а также отклонения эффективного профиля показателя преломления от параболического частота осцилляции траектории луча будет зависеть от его амплитуды, что приводит к расфазированию лучей и усреднению их фаз на некотором расстоянии z_M. Фазовая ячейка при этом расплывается и переходит в кольцо в фазовом пространстве, которое при дальнейшем распространении излучения вдоль волновода не меняет своей формы (рис. 2) . Однако на коротком начальном участке z « z_M лучи в определенных сечениях окажутся сфазированными и поле будет повторять поле на входе.

Это явление можно использовать при конструировании фильтра мод, работающего в режиме согласования, при котором конечные ширины мод и лучей постоянны, а конечные траектории центров мод и лучей имеют такой же функциональный вид, как начальные. Согласование достигается периодически с периодом, равным периоду осцилляции луча в изгибе, причем длина изогну того участка 1 должна удовлетворять условию 1 « zM.

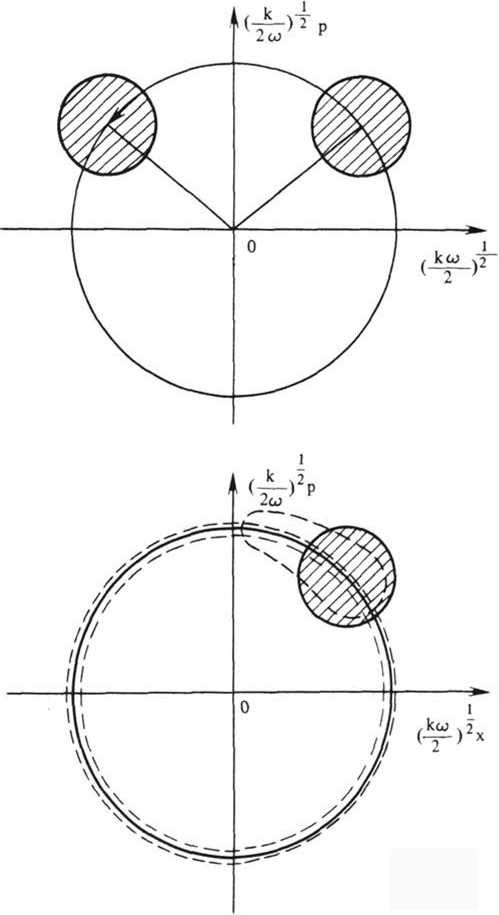
Рис. 2

На расстояниях z » z^ информация о фазах лучей теряется и поле Удобно описывать с помощью мод, коэффициенты связи между которыми опре деляют модовый состав конечного излучения.

Коэффициенты связи между модами

Для исследования коэффициентов связи между модами воспользуемся Результатами работ [6,7].

Коэффициенты связи W^1, между модами изогнутого участка 1п*> и начальными модами lm> определяются квадратами модулей интегралов перекрытия Т™, = <п' |ш> , выражения для которых были получены в [ 6,7] . Для п 1 рассматриваемой задачи т" - Timin''Г* H^.to, т)

To

, 2/ ш to¹ i

to + to'1

exp {-

к to to'

7 co+to *

^эфф^'

где:

co1              1

a = —:—г (2k to)1 A co+to*             эфф'                                                              (E т = -    1 (2кш*)^Д ..

to+to               эфф

H (a, т) - полиномы Эрмита от двух переменных [9]. mn

Полезными при вычислениях могут оказаться реккурентные соотношения для интегралов перекрытия:

ТП’ m+1

lTn‘ + l(_HL)i тп*-1 4-1 Е m+F m

₊ 1    6 to' _Tn'

Е /г^1 ш m

ТП*+1 m

-             Tm

i

>

(9а)

Tn* =£(m)iтn, _ l(n^l)i Tn*+1 4+1 n m+1   m-1 n m+1 m

_Tⁿ'+1__E, n* _? j _Tⁿ'-1 ₊ 1 _f m+l >I

4      nn^T  Tm   + n n^+T1

1 6   /У1)i n 471 “

,n m+1

Tn m

>

- - " ⁶ Tⁿ' n /п'+l ^{m z}

где

2 /to to1

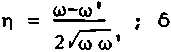
(kto j i 2

A * эфф

(9в)

(9r)

(9д)

Коэффициенты связи между модами начального и конечного прямолинейных участков волновода при длине изогнутого участка будут определяться выражением

W™" = Е W1' W?" ,                                                        (1°)

п 1 • п 1   '

где:

wn ~ коэффициенты связи между модами начального прямолинейного и и изогнутого участков волновода, определяемые из выражения (7);

^^• ~ коэффициенты связи между модами изогнутого и конечного прямолинейного участков волновода, которые можно рассчитывать при помощи (7) , переменив to и со* местами и положив

= (1 - /1 +         г/4

Эфф               ш2 г2

Суммирование в (10) ведется по всем направляемым модам изогнутого участка.

Используя вид коэффициентов связи, нетрудно показать, что непрерыв-d д ное и достаточно медленное (—^- “ « 1) изменение радиуса изгиба не вызывает перераспределения энергии между модами. Это явление дает другую возможность использования изогнутого волокна в качестве фильтра мод, работающего в режиме согласования. Такой фильтр будет состоять из волокна, изогнутого по спирали, причем число направляемых мод будет определяться наименьшим радиусом кривизны спирали.

Потери

Потери в изгибах волноводов вызываются перераспределением энергии между модами волновода, в результате которого часть энергии направляемых мод переходит в моды излучения. Если по начальному прямолинейному участку волновода распространяется пучок света с энергией Ро, то энергию направляемого излучения на конечном прямолинейном участке можно оценить по формуле где:

М - число начальных возбужденных мод;

N - число направляемых мод данного волновода;

М

₽т - энергия m-й начальной моды, причем Е Р = Ро.

т=0

Для реальных световодов с градиентным параметром щ ~7*10-3 мкм-1 и шириной 2а ~60 мкм количественная оценка показывает, что перераспределение энергии, а следовательно, и потери становится существенным при Радиусах г ~2-10“ мкм. При дальнейшем уменьшении радиуса изгиба потери быстро увеличиваются, и при радиусах порядка г -2-102 мкм все излучение покидает волновод.

Другой вид потерь обусловлен туннелированием волны через внешнюю границу световода и рассмотрен в [4]. Потери энергии на туннелирование в данной моде зависят от показателя преломления внешней среды и возрастают с увеличением порядкового номера моды. Это дает возможность использовать изогнутые волноводы в качестве перестраиваемых рефрактометров, чувствительность которых можно менять путем измерения на выходе волновода энергий различных мод. На практике выделение из пучка света, получаемого на выходе волновода, данной поперечной моды можно осуществить с помощью пространственных фильтров, синтезируемых на ЭВМ [10, 11].