Формирование время-частотных представлений (динамического спектра) нестационарного сигнала на основе преобразования представлений известного типа

Нестационарность сигнала в информационноизмерительных системах (ИИС) проявляется изменением во времени частотной структуры его спектра. Целью обработки и анализа таких сигналов является интерпретация динамического спектра, который, по сути, является время-частотным представлением сигнала. Представление (по методу и теоретической базе) относится к одному из двух классов: время-частотному классу Коэна или к аффинному время-масштабному классу вейвлетов [1–3]. До последнего времени методология формирования время-частотных представлений (ВЧП) этих двух классов считалась достаточно полной и законченной. Однако в последние годы предложены средства создания новых групп ВЧП на основе преобразования существующих типов двумерных представлений сигнала. Папандреу и Хлавачем (Papandreou, Hlawatsch [4, 5]) построена группа ВЧП с использованием ковариационного принципа, ориентированного на гиперболическое или степеннóе преобразования временнóй переменной сигнала. Затем проведена разработка, связанная с обобщением форм и способов порождения новых видов ВЧП и использованием элементов функционального анализа [6, 7]. К сожалению, группы новых ВЧП, образующие подобие классов, пока не нашли собственной ниши в области при- ложений по обработке нестационарных сигналов. Хотя следует сказать, что от времени появления двух традиционных классов ВЧП (класса Коэна и аффинного класса вейвлетов) до применения их в исследованиях и технических разработках прошло по меньшей мере 4–6 лет.

Ниже рассматриваются общие аспекты формирования классов ВЧП и принципы, используемые для расширения классов таких представлений сигнала. Метод получения ВЧП имеет общий характер, поэтому там, где это допустимо, термин ВЧП сохраним для обоих классов. Это возможно, поскольку параметр a масштаба вейвлетов пропорционален обратной частоте a = f 0 / f и может рассматриваться как гиперболическая частотная шкала представления динамического спектра.

Метод формирования многообразия ВЧП дает прямую характеристику всех квадратичных время-частотных представлений нестационарного сигнала на основе концепции ковариантности ВЧП к некоторому общему классу преобразований сигнала (называемых унитарными). Общность рассматриваемых преобразований состоит в том, что они имеют два непрерывных параметра и являются отражением лежащей в их основе группы. При этом оказывается возможным описать все ВЧП сигнала с помощью унитарных преобразований, применяемых к элементам хорошо известных классов: класса ВЧП Коэна и класса аффинных вейвлет-представлений сигнала.

О ТЕРМИНАХ, ПОНЯТИЯХ И ОБОЗНАЧЕНИЯХ

Для описания метода формирования отдельных видов ВЧП на основе представления известного типа удобно использовать некоторые термины и обозначения, нетрадиционные для приложений по обработке сигналов ИИС. В теории таких приложений применяются обозначения: L(R) — многообразие интегрируемых сигналов или функций; L²( R ) — интегрируемые с квадратом функции (включая все сигналы с конечной энергией); R — все вещественные числа; L²( R ²) — интегрируемые с квадратом двумерные представления сигнала; Z — совокупность всех целых чисел (<0; 0; >0). Пределы ± ” у интеграла могут не указываться.

Понятие группы G включает совокупность элементов, связанных рефлексивностью ( a ~ a ), симметричностью ( a ~ b ^ b ~ a ), транзитивностью ( a ~ b и b ~ c ^ a ~ c ), наличием единичного (нейтрального) элемента e и обратных элементов ( ae = a ; a ^-1 : aa ^-1 = e ). Операцию в группе обозначают определенным символом, например "  • ".

Термин унитарность относится к преобразованию функций (например, U a : s(t ) ^ s ( at )), обладающему следующим свойством. Для унитарного преобразования (УП) U его сопряженное U * совпадает с обратным ( U * =U ^-1), где сопряженность понимается как эквивалентность перестан _* овки оператора U (с заменой на сопряженный U ) на другой множитель скалярного произведения (интеграла произведения) двух функций:

U s 1 ( t ), s 2 ( t )) = ( s 1 ( t ), U * s 2 ( t )), или

J [ U s 1 ( t ) • s ₂ ( t )] d t = J [ s 1 ( t ) • U * s ₂ ( t )]d t .

Аналогом унитарности является привычное требование выполнения для матриц свойства транспонированной перестановочности и ортогональности, которые для матрицы А имеют вид: AA ^T = A ^T A = I ; A ^T = A ^-1 ( A ^T — транспонированная матрица, A ^T = [ a ij ], a j = a ji , V i,j ; A ^-1 — обратная матрица, I — единичная матрица).

Далее, поскольку метод основан на преобразованиях, то термин ВЧП интерпретируется как время-частотное представление (а не преобразование), что соответствует двумерному представлению сигнала (а точнее его спектра) в плоскости время—частота. В логике построения ВЧП заложено прагматичное требование, чтобы при смещении их аргументов (времени и частоты) само значение ВЧП менялось по определенному и простому правилу, так чтобы результат такого смещения было легко оценивать. Правило, по которому в этом случае изменяется значение ВЧП, называется ковариационным свойством. Так, если Tn — операция (далее "оператор") сдвига времени у сигнала s(t) — Tns(t) = s(t - n), а операция Fm — это операция сдвига частоты у того же сигнала (в частотной форме1)) — Fms(f) = e2njmf$(f), то представление С класса Коэна для сигнала при одновременном сдвиге у него времени и частоты (согласно свойству, называемому ковариантностью) определяется соотношением

( C • { F m • T n • s } )( t , f ) =

= ( C • s )( t - n , f - m ) при m , n e R .    (1)

Выражение (1) справедливо для ВЧП класса Коэна. В представлениях аффинного класса ковариантность относится к операциям сдвига времени и изменения масштабирующего параметра a . Это — операция T n с прежним значением и операция D _d : D d s ( t ) = | d | ^1/2 • s ( 11d ) . В представлении Q аффинного класса для сигнала с одновременным сдвигом времени и изменением масштабирующего параметра свойство ковариантности выражается соотношением

( Q - { T n • D d s } )( t , f ) = ( Q • s ) f t - n , d • f ) . ⁽²⁾ V d )

Отметим, что логика свойства ковариантности связана с необходимостью минимальной коррекции представления сигнала при изменении положения исследуемого сегмента сигнала, при смене необходимого частотного диапазона анализа или при изменении скорости регистрации сигнала. При этом у двух классов представлений свойство кова-рантности относительно преобразования аргументов отличается в связи с тем, что эти преобразования отражают операции, свойственные двум различным группам 2). Это группа Вейля—Гейзенберга (у ВЧП класса Коэна) и собственно аффинная группа (у класса аффинных представлений вейвлетами).

ПРЕОБРАЗОВАНИЕ ВЧП: ДВА КЛАССА ПРЕДСТАВЛЕНИЙ НЕСТАЦИОНАРНОГО

СИГНАЛА

Квадратичные время-частотные представления сигнала нашли широкое применение в прикладных исследованиях и технических разработках, требующих контроля зависящего от времени (динамического) спектра [11-13]. В то же время дву- мерное распределение энергии сигнала по времени и частоте (динамический спектр мощности) имеет не единственную процедуру получения, т. к. существует много различных ВЧП и способов формирования такого распределения [14]. Преобладают два класса представлений: класс Коэна, ковариантный к сдвигу времени и частоты сигнала, и аффинный класс, ковариантный к сдвигу времени и изменению масштаба. Основную часть последнего класса составляют представления сигнала вейвлетами [15–16].

Поскольку операции сдвига времени, сдвига частоты и изменения масштаба не являются единственными важными преобразованиями сигнала, то недавно были предложены некоторые новые классы ВЧП. Один из классов соответствует различным видам гиперболического преобразования, в котором ковариантность относится к "гиперболическому" сдвигу времени и изменению масштаба [4]. Другой класс построен на основе ковариантности к "степеннóму" сдвигу времени [5]. Обобщенный подход в направлении формирования нового класса ВЧП введен Баранюком и Джонсом (Baraniuk, Jones) [8, 17]. Для этого предложено использовать метод унитарного преобразования 3). Метод расширяет группу классов ВЧП, ковариантных к разнообразию преобразований сигнала, и не слишком сложен, если не считать непривычности терминологии.

При рассмотрении время-частотных представлений класса Коэна и аффинного класса для сигнала s ( t ) используется операторное обозначение ( P s)( t , f ), где t и f — аргументы (время и частота) двухпараметрического ВЧП сигнала; оператор P реализует преобразование L 2 ( R ) ^ L 2 ( R 2 ), т. е. и сигнал, и ВЧП интегрируемы с квадратом (причем ВЧП — по двумерной области своих аргументов). Каждое квадратичное ВЧП ⁴⁾ класса Коэна может быть выражено соотношением [15, 18]

( C 5 )( t , f ) = JJ ( A 5 )( e , т ) _¥ ( е , т )е - j ') d e d r , (3)

где ^ ( е , т ) — функция-ядро, определяющая вид ВЧП; ( A 5 )( е , т ) — двойственная функция, симметричное квадратичное двухпараметрическое представление сигнала, единое для всего класса ВЧП Коэна:

( A 5 )( е , т ) = Г 5 ( t + - Y 5 * ( t - - ) e j d t .   (4)

I ² J I ² J

ВЧП, порождаемые определенным фиксиро- ванным ядром, ковариантны к оператору сдвига времени (Tn5)(t) = 5(t - n) и оператору сдвига частоты (F m5)( f ) = e 2nmf5( f ).

Для ВЧП C класса Коэна при совместном действии этих операторов на сигнал свойство кавари-антности выражается соотношением

( CF m T n 5 )( t , f ) =

= ( C 5 )( t - n , f - m );     m , n e R .      (5)

Справедливо и обратное положение. Все квадратичные ВЧП, обладающие свойством ковариантности в такой форме, должны принадлежать классу Коэна.

Ковариантность к переносу (смещению) времени и частот является следствием того, что эти операторы представляют отображение на пространство функций L²( R ) группы Вейля—Гейзенберга, которая характеризуется свойством [8–10]:

( Fm T )( Fm T ) = e - j ² ” 1 F ₊m T ₊ „ •   (6)

m j n j      m 2 n 2                   m ] + m 2 n ] + n 2

Каждое ВЧП в аффинном классе может быть выражено соотношением

( Q 5 )( t , f ) =

= JJ ( A 5 )( e , T ) _¥ | e ; f . T | e-^^{nj( e t +T} f ) d e d T .    (7)

V f J где ^(e, t) — функция-ядро.

Аффинное ВЧП, порождаемое фиксированными ядрами, ковариантно по отношению к оператору сдвига времени и оператору изменения масштаба ( D d s )( t ) = | d I ^1/2 • 5 ( 11 d ). При одновремен -ном действии на сигнал операторов ( T n 5 )( t ) = 5 ( t - n ) и ( D _d 5 )( t ) ^| d | ^{- 1/2} • 5 ( t / d ) свойство ковариантности выражается соотношением

( QT n D d 5 )( t , f ) = ( Q 5 ) | t

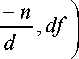
Так же, как и для класса Коэна, форма ковариантности в виде соотношения (8) характеризует принадлежность ВЧП к аффинному классу время-масштабных представлений сигнала посредством вейвлетов. Другими словами, все время-частотные преобразования, ковариантные таким образом, должны принадлежать аффинному классу.

Аффинная ковариантность для этих ВЧП является следствием того, что T и D составляют унитарное отображение на L²( R ) аффинной группы со свойством

( T n D d 1 )( T n 2 D d 2 ) = T n i + d 1 n 2 D d 1 d 2 .       (9)

УНИТАРНАЯ ЭКВИВАЛЕНТНОСТЬ ВРЕМЯ-ЧАСТОТНЫХ ПРЕДСТАВЛЕНИЙ СИГНАЛА

Для того чтобы найти подходящее преобразование сигнала, которое отличается от сдвига времени, сдвига частоты и изменения масштаба, были разработаны два класса представлений сигнала. Один из них включает гиперболические ВЧП, ковариантные к изменению частоты и "гиперболическому сдвигу" времени [4]. Другой класс представлений включает ВЧП, условно называемые степенными и обладающие ковариантностью к изменению масштаба и "степенному сдвигу" времени [5]. Хотя оба класса оказалось возможным вывести с помощью использованной разновидности ковариантности, в рамках рассматриваемого метода они могут быть получены путем непосредственного преобразования ВЧП [6–10]. Каждое представление гиперболического класса может быть выражено в виде VCU , где C — ВЧП класса Коэна; U — унитарное преобразование сигнала ( U: L²( R ) ^ L^r( R )); V — унитарное преобразование переменных ВЧП ( V: L²( R ) ^ L 2 ( R )) [4]. Аналогично каждое представление степеннóго класса может быть выражено в виде VQU , где Q — ВЧП аффинного класса; U — унитарное преобразование сигнала ( U: L 2 ( R ) -> L 2 ( R ) ); V — унитарное преобразование переменных ВЧП ( V: L²( R ) -> L 2 ( R ) ) [5]. Преимущество такого метода в общности формы порождения нового класса ВЧП, и отчетливая логика его реализации: предобработка сигнала соответствующим оператором U, получение ВЧП класса Коэна ( C ) или аффинного класса ( Q ) для преобразованного сигнала ( U s ) и выполнение унитарного преобразования ( V ) полученного время-частотного представления . (Последнее преобразование ( V ) называют также искривляющим (warping transformation) координатные оси переменных ВЧП).

Преобразование классов Коэна и аффинного не ограничивается только гиперболическим и степенным классами. Согласно анализируемому здесь методу, варьирование U и V может вести к получению других видов классов, преобразованных из классов Коэна и аффинного. Преобразованные классы являются ковариантными не к сдвигам времени и частоты и изменению масштаба сигнала, а к операторам T _n , F _m , D _d , которые унитарно эквивалентны традиционным операторам T _n , F _m и D d :

T n = U ^{- 1} T n U ; F m = U ^{- 1} F _m U ; D d = U ^{- 1} D d U . (10)

Чтобы увидеть это, оставим на время в стороне оператор V и рассмотрим два соотношения, определяющие действие ВЧП C класса Коэна и ВЧП Q аффинного класса на результат предобработки

(оператором U) сигнала s, видоизмененного дей-~~  ~~ ствием операторов FmTn и TnDd :

( CUF m T n S )( a , b ) = ( CU s )( a - n , b - m );     (11)

( QUT n D d S )( a , b ) = ( QU s )| —- I d

, db

/

При получении выражений (11) и (12) использовано свойство коммутируемости операторов (возможности перестановки их местами), которая обусловлена унитарностью.

Представления с предварительной обработкой CU и QU (предобработанные представления) поддерживают переносы и аффинную ковариантность, свойственную представлениям, из которых они выведены. Это происходит потому, что пары операторов F _m ; T _n и T _n ; D _d остаются унитарными отражениями на L²( R ) групп Вейля— Гейзенберга и аффинной группы соответственно. Для лучшего понимания достаточно сравнить выражения (11) и (5) , а также (12) и (8).

Таким образом, преобразованные класс Коэна и аффинный класс являются унитарно эквива- лентными первоначальным классам: первоначальному классу Коэна и первоначальному аффинно- му классу.

В то время как координаты ( a,b ) преобразованных распределений CU и QU не соответствуют времени и масштабу (фактически они соответствуют физическим величинам, связанным с операторами T _n и F _m или T _n и D _d ), после преобразования оператором V время-частотное представление (постобработанное представление сигнала) может получить искривление своих координат ( a,b ) в новые координаты. Тем не менее, эти новые (искривленные, или warped) координаты обеспечивают достаточно точную время-частотную локализацию элементов динамического спектра. Степень этой локализации (снова из-за унитарности преобразования) не хуже, чем у представления до его модификации [8].

Если дано фиксированное U , то процедура определения соответствующего V выполняется непосредственно: мы просто искривляем оси распределений функциями A ( t , f ) и B ( t , f ), которые описывают групповую задержку и мгновенную частоту преобразованных собственных функций U^-1 8 ( x ~ - a ) и U”¹ e² ” j ^bx операторов F и T соответственно. Для распределений преобразованного класса Коэна полагается:

( VCU s )( t , f ) = ( CU s )[ A ( t , f ), B ( t . f )].    (13)

Рассмотрение преобразованного аффинного класса производится аналогично.

Унитарная эквивалентность двух ВЧП VCU и VQU приводит к тому, что они остаются ковариантными к операторам FmTn и TnDd соответственно, хотя V искривляет групповые действия (11) и (12) вдоль групповой задержки и кривых мгновенной частоты преобразованных собственных функций5).

Принцип унитарной эквивалентности в определенной степени несложен по концепции, и это делает доступным изучение свойств унитарно эквивалентных ВЧП, т. к. свойства преобразованного класса могут быть немедленно получены из свойств класса Коэна или аффинного класса путем простой процедуры их изменения. Мы просто везде заменяем s на U s и искривляем оси координат в результирующем ВЧП.

ЭЛЕМЕНТЫ УНИФИЦИРОВАННОЙ ТЕОРИИ ДЛЯ КОВАРИАНТНЫХ ВЧП

Унитарная эквивалентность обеспечивает простое средство получения набора различных классов ВЧП. Однако априори не очевидно, что рассматриваемый метод исчерпывает все возможные ковариантные ВЧП. Например, унитарно эквивалентные ВЧП ограничены (в пределах "искривляющего" преобразования V ) двумя видами ковариантности, связанными с группой Вейля—Гейзенберга и аффинной группой. Причем новые ВЧП наследуют виды ковариантности соответственно из класса Коэна и аффинного класса. В [8] это интерпретировалось как ограничение метода, поэтому полезно несколько более развернутое рассмотрение основных элементов теории ковариантных ВЧП.

Ковариантные время-частотные представления

Формулирование основных положений будет характеризовать ВЧП, ковариантные классу двухпараметрических унитарных преобразований сигнала G ( p , q ) . Эти положения обобщают операторы время-частотного сдвига и время-масштабного изменения (традиционно используемые и естественные для ВЧП класса Коэна и аффинного класса).

Физическое рассмотрение (обратимости, совместного последовательного действия — правила композиции операторов и др.) показывает, что каждое из этих преобразований должно быть представлением унитарной группы с законом умножения (композиции) " • " [9, 10]:

G G =G ( P i ,q i )    ( p 2 , q 2 )          ( P i ,q i ) * ( p 2 , q 2 ) "

Время-частотное представление ( P s)( t , f ) считается ковариантным к G _{( p , q )} при условии выполнения соотношения

( PG ( p , q ) 5 )( t , f ) = ( P 5 )( t , f ) о ( p , q ), (15)

где "  о " — означает отображение G ( _{p q} ) (результат преобразования сигнала) на время-частотную плоскость, т. е. сопряженно-связанное G _{( p , q )} представление в этой плоскости.

Свойство, присущее G _{( p , q )} (его группе), позволяет представить выражение (15) в развернутом виде соотношением

( ^PG ( A, q 1 ) ^G ( p 2 , q 2 ) 5 )( t , f ) =

= ^{( P 5 )(} t , ^f ) ^{0 [(} p 1 , q 1 ) • ⁽ p 2 , q 2 ).       (16)

Такой подход к трактовке ковариантности отражен в работах Хлавача и Болькски (Hlawatsch, Bolcskei) [6, 7]. В их интерпретации G является оператором время-частотного смещения, причем символ "  о " означает связанную с ним функцию смещения.

В качестве примеров операторов смещения и функций можно привести следующие.

• 1)    G ( m , n ) = F m T n     и     ( C { F m T n S } )( t , f ) =

= ( C 5 )( t - n , f - m ) — для ВЧП класса Коэна⁶⁾.

• 2)    G ( m , d) = T n D d       и    ( QT n D _d5 )( t , f ) =

I t - n       I

= ( Q 5 ) l---- , df I — для ВЧП аффинного класса.

( d     )

• ^{3)    G} ( m , n ) = F m T n = ^U " ^{1 F} m ^T n ^U , а также вариант ( CF _m T _n5 ) ( t , f ) = ( C 5 )( t - n,f - m) с искривлением координат ( t , f )-представления посредством A ( t, f ), B ( t , f ) — для унитарно эквивалентных ВЧП класса Коэна.

  _-

  
  

• 4)    G ₍ n , d ) = U- 1 T, D _d U      а также вариант

( QT _n D _d 5 )( t , f ) = ( Q 5 ) f t—n , df ) с искривлением

I d )

координат ( t , f )-представления посредством A ( t, f ),

B ( t , f ) — для унитарно эквивалентных ВЧП аффинного класса.

Общее положение о методе унитарной эквивалентности при создании новых классов время-частотных представлений сигнала

Унитарная эквивалентность порождает ВЧП, ковариантные большому числу различных двухпараметрических операторов смещения G . Можно показать, что, кроме этих, не существует других ковариантных ВЧП. Другими словами, простая процедура унитарной эквивалентности (описанная выше) обеспечивает достаточное количество ковариантных ВЧП, чтобы характеризовать весь их набор.

Общее положение, связанное с реализацией унитарной эквивалентности, состоит в следующем. Для того чтобы быть унитарным представлением группы, оператор смещения G , определяющий свойства ковариантности класса ВЧП, должен подчиняться соотношению (14). Поэтому классификация всех ковариантных ВЧП равноценна классификации двухпараметрических групп (без учета фазы), которые могут действовать на пространстве сигналов (L²( R )). Установлено, что есть только два вида таких групп: группа Вейля—Гейзенберга, которая соответствует оператору смещения вида G = U - 1 FTU , и аффинная группа, которая соответствует оператору смещения вида G = U ^{- 1} TDU. Классы ВЧП, ковариантные к этим операторам (операциям) смещения, соответствуют унитарной эквивалентности классу Коэна и аффинному классу. Это позволяет сформулировать общее положение о методе унитарной эквивалентности следующим образом.

Все квадратичные время-частотные представления сигнала , которые ковариантны (в смысле соотношений (14-16) и их трактовки), могут быть представлены в форме VCU или VQU , где C — ВЧП класса Коэна; Q — ВЧП аффинного класса; U — унитарное преобразование сигнала; V — двумерное преобразование в области переменных ВЧП (времени и частоты), описанное выражениями (11–13) и пояснениями к ним. (Функциональный смысл преобразований U и V описан выражениями (11–13) и пояснениями к ним).

ЗАКЛЮЧЕНИЕ

Существовавшее предположение о неполноте концепции об объективности ограничения многообразия время-частотных представлений (ВЧП) сигнала только двумя традиционными классами, привело к появлению теоретически обоснованного метода порождения дополнительного набора классов ВЧП. В основу этого метода положено расширение понятия свойства ковариантности и введение нового подхода к характеристике всех ВЧП на основе унитарной эквивалентности классам Ко- эна и аффинному. Описание дополнительных групп ВЧП как унитарно преобразованных классов Коэна и аффинного имеет определенные преимущества. В частности, множество всех операторов двухпараметрических время-частотных смещений, включающее ковариантные ВЧП, ограничено до совокупности операторов типа U-1FTU или U-1TDU. Кроме того, каждый класс ковариантных ВЧП может соответствовать только либо классу Коэна, либо аффинному классу; в связи с этим нет необходимости осуществлять дополнительные исследования способов получения других классов ВЧП, исходя из каких-либо новых концепций. Метод порождения новых классов ВЧП и его полнота базируются на работах Хлавача, Болькски, Папандреу, Будро-Бартлета, Баранюка и Джонса [4–8].