Formula for natural frequency oscillation truss with an arbitrary number of panels

The value of a structure's fundamental (first) natural frequency is the most crucial parameter for solving the dynamics problem. Traditionally, this value is calculated for complex structures by the finite element method [1], [2]. With the development of computer mathematics systems [3], it became possible to obtain analytical solutions. Among all the problems for which analytical methods are available, statically determinate rod structures of regular type stand out. These are planar and spatial trusses, the periodic element of which is a panel of several rods. Regular constructions were studied in the works of Ignatiev V.A. [4] and Kaveh A. [5]. The existence of statically determinate constructions was raised in [6] and [7]. The handbook [8] contains various schemes of planar regular trusses and formulas for the dependences of the deflection and displacement of movable support on the number of panels and loads of several types. Analytical solutions for the first (main) natural frequency were obtained within the framework of the approximate Dunkerley approach [9], [10]. Based on the calculation of partial frequencies, this method gives a lower estimate of the first frequency. The upper estimate is obtained using the Rayleigh energy method [11], [12]. Calculation formulas using the Rayleigh method are more complex and cumbersome than those using the Dunkerley method. In [13] and [14], simplified methods for calculating the first frequency are proposed. Algorithms for deriving analytical solutions to problems of the stress-strain state of structures in the Maple computer mathematics system using the superposition method and expansion of solutions into series in terms of initial functions are considered in [15], [16]. The problem of a spatial truss in a nonlinear formulation was solved by V.V. Galishnikova [17]. A lower analytical estimate for the fundamental natural frequency of a planar regular truss was obtained in [18]. The formula for the first frequency of natural vibrations of the spatial model of an L-shaped bracket was derived by the induction method in [19]. The fundamental frequency of a planar Fink truss was calculated analytically in [20]. The static deflection of a planar truss for an arbitrary number of panels in the Maple system was calculated in [21]. The analytical dependence of the first frequency of free vibrations of a planar two-span truss was obtained in [22]. In [23], using the Dunkerley method, an analytical calculation of the first frequency of a flat statically determinate trussed structure was performed.

This paper considers a new scheme of a planar statically determinate regular truss with a reinforced lattice. Due to the vertical truss elements, the lengths of the upper chord rods are reduced, increasing their stability. The mass of the truss is evenly distributed among its nodes. The task is to obtain an analytical dependence of the truss's main (first) natural frequency on the number of panels using the Dunkerley partial frequency method and the proposed method, which simplifies and refines the solution. Both solutions are compared with the numerical one. For higher frequencies, spectra of trusses of various orders are constructed and studied. The goal is to identify practically significant features of the frequency distribution. The resulting calculation formulas can serve as a simple and fairly accurate estimate of the first vibration frequency of the designed structure.

• 2    Materials and Methods

2.1 Truss scheme, drawing up equations

The planar truss model has 2 n panels per span and consists of n = 16 n + 4 elastic hinged rods, including three rods corresponding to the left movable and right fixed supports (Fig. 1). The rods of the upper compressed chord are two times shorter than the rods of the lower stretched chord, which increases the stability of the structure concerning the stability of the chords.

Fig. 1. - Truss scheme, n=4

The method of cutting nodes is used [24] to determine the forces in the rods. Analytical transformations associated with the compilation and solution of a system of algebraic equations for the equilibrium of nodes are performed in the Maple system. The reference system is introduced, and the coordinates of the nodes are specified. The origin of coordinates is in the left movable support A (Fig. 2):

xi = (i -1) a, yi = 2 h, i = 1,...,4 n +1, xi+4 n+1 = (2 i — 1) a, yi+4 n+1 = h, i = V-,2 n, xi+6 n+1 = 2( i -1) a, yi+6 n+1 = 0, i = 1,...,2 n +1.

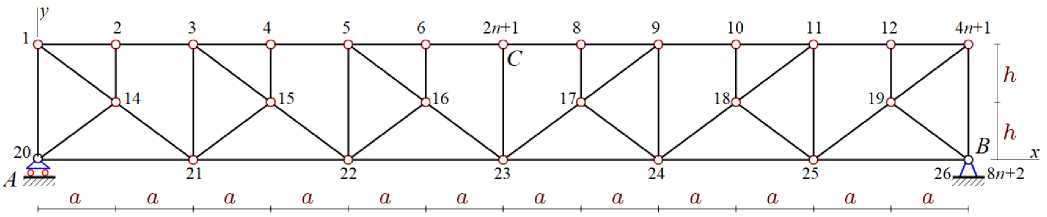
Fig. 2. - Numbering of truss nodes, n= 3

The topology of the lattice is determined by the order in which the truss bars are connected into nodes. The truss rods are assigned lists of their end numbers to do this. The lists are oriented, but the choice of beginning and end does not affect the sign of the effort and its magnitude. The following lists of numbers correspond, for example, to the top chord bars:

Ф i = [ i , i + 1], i = 1,..,4 n .

Bottom chord rods:

Ф. . = [6 n + 1 + i ,6 n + 2 + i ], i = 1,..,2 n .

i + 4 n

Other rods are coded similarly, including three support rods (one vertical rod is a movable hinge, and two are fixed).

2.2    Calculation of forces in rods

A system of equilibrium equations for nodes GS=B is compiled and solved to find the forces in a statically determinate truss. G is a matrix whose elements are the direction cosines of the forces in the rods. Here, S is the vector of all unknown forces and reactions of the supports, and B is the vector of nodal loads. For the equilibrium equations of each truss node, two rows are allocated in the matrix G , and in the load vector, there are two elements with the same numbers. The projections of external forces applied to node i onto the x-axis are included in the odd elements of the load vector B _{2 i - 1} and the even elements — the projections of forces on the y -axis. The direction cosines of the force vectors have the form:

l • = (x^  — x^  ) / l, l • = У  — У.,.  ) / l, i = I, — , У, x,i Ф . Ф t'  У,i \аФ Ф i

,                        i,1                  i ,2                      y,                       i,1

where l. = л /l2 +12 is the length of rod i. Matrix G elements on even and odd rows: i              x, iУ

G = l / l ,, G . = l / l ,

2 Ф i ₁ - 1, i         x , i ¹ i' 2 Ф i 1 , i         y , i ¹ i'

G^    = - l / l , G^   = — l / l •

2Ф i2 —1, i            x, i       i' 2Ф i2, i            y, ii

The direction cosines of forces applied to different ends of the same rod have different signs.

2.3    The first natural frequency of oscillations

The standard inertial model of a truss, intended for calculating natural frequencies, assumes that the entire mass of the truss is distributed evenly over its nodes. All masses m have one degree of freedom — movement along the vertical axis y. Thus, the number of degrees of freedom of the system equals the number of nodes K = 8 n + 2 . The system of differential equations of mass motion is written in matrix form:

M K Y + D K Y = 0                            (1)

where Y is the vector of displacements of all K masses, D _K is the rigidity matrix of the system, M _K is the inertia matrix, Y and is the vector of mass accelerations. In the case of identical masses, the inertia matrix is proportional to the unit matrix M K = m I K . If we multiply equation (1) on the left by the compliance matrix B _K , inverse to the stiffness matrix D _K . In that case the problem can be reduced to the problem of eigenvalues of the matrix B K : B K Y = X Y , where X = 1 / ( m ш ² ) is the eigenvalue of the matrix, B K ш and is the natural frequency of oscillations. The compliance matrix B K is found using the Maxwell–Mohr formula:

b . = у S ⁽ i) S ⁽ j l /(EF ),                                    (2)

• i ,    j              a a a

a = 1

where S^¹ ) is the force in rod a from the action of a unit vertical external force on node i . The oscillation frequency is expressed through eigenvalues X of the compliance matrix B K and has the form:

ш = 1 / ( m X )                                       (3)

In the general case, it is impossible to analytically solve the problem of natural vibrations of a truss with many nodes. However, there is an approximate method for finding the lower limit of the first frequency, allowing an analytical solution. Dunkerley's formula gives a lower bound for this frequency:

K

“ » = У^'

Di i=1

where ш . is the partial frequency of vibration of mass m located at node i . It is enough to use the scalar form of equation (1) to calculate partial frequencies ш :

mu. + du. = 0, i ii

• — equation of oscillation of one independent node, where u_i is the vertical displacement of the mass,

• u. is its acceleration vector, d. is the stiffness coefficient ( i is the number of the truss node with mass ii

• m ). The oscillation frequency of an individual load located at node i : ш. = dd. / m . According to the

Maxwell–Mohr formula, the stiffness value is calculated through the compliance coefficient:

za\2

« = 1/ d . = E ( S , ⁾ ) I, /(EF )                             (5)

a = 1

From (4) and (5) it follows:

• к          K         K ^

шD^ = m E у = m E « = m EE ( S^ ) l _a / (EF ) = m E .

= 1 di         i = 1            i = 1 a = 1

Analytical calculation of values E in the Maple system for various values of the truss regularity order n gives the following sequence:

n = 1: S = (10a3 + 8c3 + 37h3)/(2EFh2), n = 2: S = (224a3 + 76c3 +167h3) / (4EFh2), n = 3: S = (4598a3 + 804c3 +1363h3) / (18EFh2), n = 4: s = 9(688a3 + 72c3 +107h3)/ (8EFh2), n = 5: S = (18506a3 +1280c3 +1757h3)/ (10EFh2),...

where c = 7 a ² + h ².

The coefficients of the general term of the sequence E = (C 1 a ³ + C₂c ³ + C ₃ h ³)/ (h ² EF ) are determined by the methods of the Maple system from the solution of linear homogeneous recurrent equations:

C 1 = (128 n ⁴ + 140 n ² - 45 n + 2) / 45,

C ₂ = (16 n ² - 3 n - 1)/3,                                              (6)

C 3 = (32 n ³ + 44 n ² + 34 n + 1) / (6 n ).

As a result, the desired lower estimate of the first natural frequency of free vibrations of the truss using the Dunkerley method takes the form:

ш

D

= h

EF m (C1a3 + C2c3 + C3 h3)

• 3    Results and Discussion

  3.1    Simplified Dunkerley method

Even though the resulting formula (7) with coefficients (6) for the first natural frequency is relatively simple, it can be further simplified. Such an algorithm is described in [13]. The Dunkerley solution involves Kirsanov, M.

Formula for natural frequency oscillation truss with an arbitrary number of panels;

K summating the squares of the reciprocal values of the partial frequencies ^6 and the subsequent i=1

generalization of the resulting sums. This part of the solution can be simplified if the summation is replaced by the product of the maximum deflection and half the number of degrees of freedom, using the K mean value theorem: S0 = ^ 6i = 6maxK / 2. It is easier to generalize and calculate these products found i=1

for different numbers n to an arbitrary case. The sequence of sums looks like:

n = 1: Z _o = 5(2 a ³ + 2 c ³ + 7 h ³)/(2 EFh ²), n = 2: S ₀ = 9(12 a ³ + 4 c ³ + 9 h ³)/(2 EFh ²), n = 3: Z ₀ = 13(38 a ³ + 6 c ³ + 11 h ³)/(2 EFh ²), n = 4: S ₀ = 17(88 a ³ + 8 c ³ + 13 h³)/(2EFh ²),...

General view of sequence elements for an arbitrary n :

S0 = (C4 a3 + C5 c3 + C6 h3) / (EFh2), where the coefficients are determined by induction:

C 4 = n (4 n + 1)(2 n ² + 1)/3,

C 5 = n (4 n + 1),                                                        (8)

C ₆ = (2 n + 5)(4 n + 1)/2.

Thus, the approximate value of the first frequency using the simplified Dunkerley method is written as:

w * = h

_______________ 6 EF _______________ m (4 n + 1)(2 n (2 n ² + 1) a ³ + 6 nc ³ + 3(2 n + 5) h ³)

Approximate solution (9) is noticeably simpler than solution (7).

To estimate the error of approximate solutions for the first frequency a _D (7) and 0 * (9), it is necessary to compare them with the numerical solution obtained for the entire frequency spectrum corresponding to the spectrum of the matrix of equation (1). The Eigenvalues operator of the Maple system gives the spectrum of the matrix in numerical form.

The elements of the compliance matrix B _K are formed in the Maple system in a double cycle according to pre-calculated magnitudes of forces S ^ i ) in all rods from the action of single vertical forces on nodes with masses:

^

b . = V S(iS(jl /(EF), i,j = 1,..,K. i, j              a a a a=1

Eigenvalues A of the matrix B _K give the frequency spectrum of the truss according to formula (3).

A numerical solution to the problem of the dependence of the first frequency on the number of panels and two analytical ones is presented by curves in Figure 3.

The mass of loads in the nodes is assumed to be m = 200 kg, the modulus of elasticity of all steel rods of the truss is MPa, the cross-sectional area is the same F = 9 cm ² , panel length a = 3 m, height h = 2 m. The analytical solutions turned out to be very close, and, with an increase in the number of panels, they came closer to the numerical solution, which was conventionally accepted as exact since when it was found, the problem of oscillation of a system with all degrees of freedom was solved and no simplifications were made.

More precisely, you can evaluate the degree of approximation of analytical solutions by entering the values of relative errors e d =| w D — w 1 | / w 1 and e * =\ w * — w 1 | / w 1 . Figure 4 shows the change in these values depending on the number of panels.

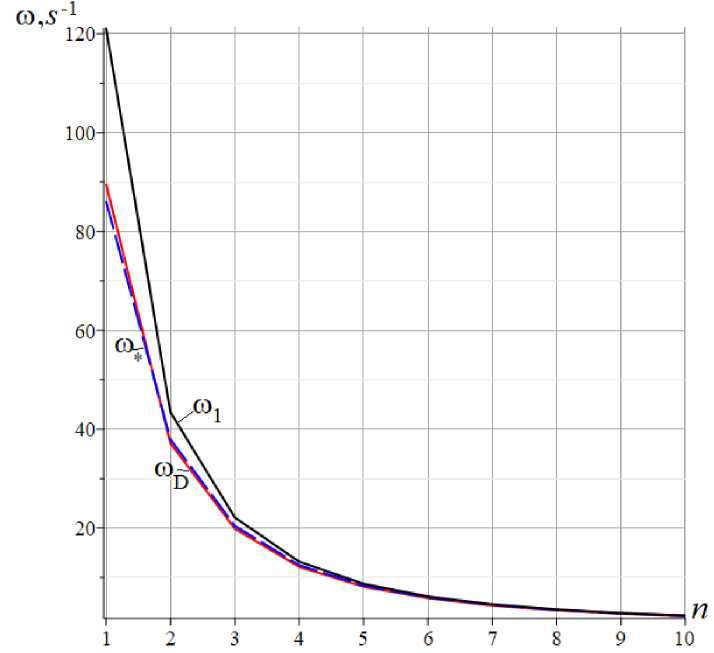
Fig. 5. –The first oscillation frequency obtained by three methods depending on the number of panelsn. The Dunkerley method wD , simplified method w*, the numerical method w 1

For n >2, the Dunkerley method has a slightly larger error than the simplified method. Starting from a certain value of n , the accuracy of both methods remains almost unchanged, reaching a completely acceptable value of several percent.

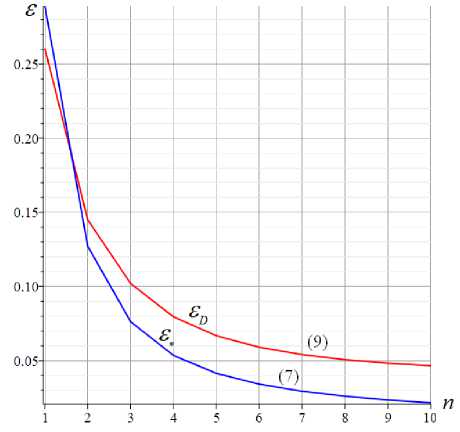
Fig. 4. –Relative error of decisions. ε _D — the Dunkerley method; ε _* — simplified method

It is known that the Dunkerley estimate of the first natural frequency of trusses is, as a rule, much less accurate than in this problem. On average, the error of this method is about 30%. The approximate analytical solution (9) was all the more interesting, which gives both a more accurate and simpler solution.

3.2    Frequency spectra of a regular truss

Frequency analysis of a structure is not limited to calculating only the first frequency. At higher system frequencies, resonant phenomena can be observed, which are very important to foresee. For regular structures of various orders, some regularities in the spectra make it possible to predict the higher Kirsanov, M.

Formula for natural frequency oscillation truss with an arbitrary number of panels;

frequencies of trusses of large order without resorting to calculations but using calculations of simple trusses of the same class. In Figure 5, the spectral frequencies obtained numerically are conventionally combined by curves of the same color. One graph shows the spectra of trusses of the order of 1, 2,...10. The abscissa axis shows the frequency numbers in its spectrum, and the ordinate axis shows the frequencies themselves. There are several patterns in this figure. First, numerical calculations show that the highest frequency for all trusses of different orders is the same. This is the highest spectral constant of the structure, constant for the selected panel dimensions, masses, and elastic properties of the material. There are several such spectral constants. In this example, this are a = 905 s - 1 , a = 748 s ^-1, a = 420 s ^{- 1} , etc. "Resonance safety zones" are also observed — intervals in the spectra of natural frequencies of trusses of various orders in which no natural frequencies exist. External oscillation drivers, for example, a motor installed on a truss, must have a natural frequency in one of these zones to avoid resonance. There are several safety zones in this task. For lower frequencies, there are no resonant safety zones, or they are very narrow, for example 224 s 1 <  a <  317 s .

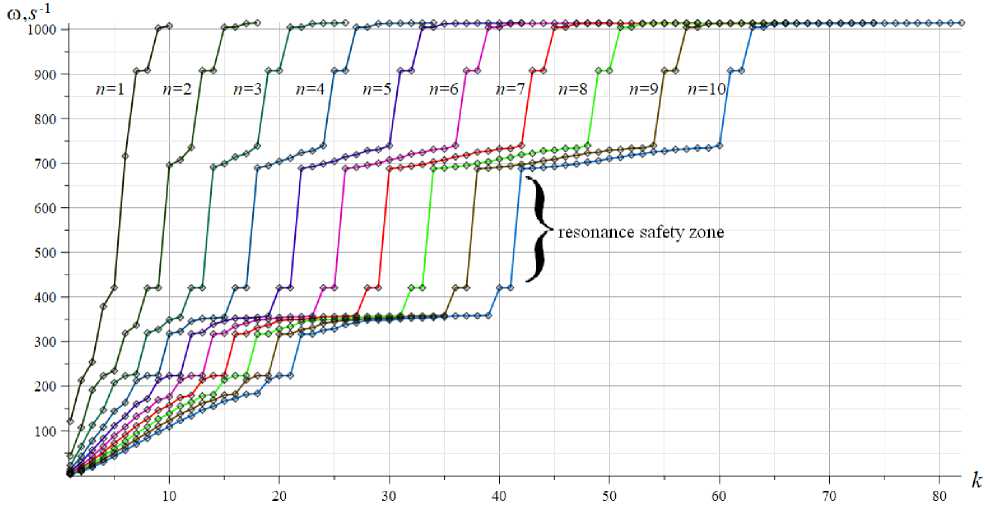
Fig. 5. – Frequency spectra of trusses of different orders

Knowledge of spectral constants and safety zones greatly simplifies the analysis of structures with many panels.

• 4    Conclusions

Main results of the work:

• 1.    A mathematical model of a planar statically determinate regular truss has been constructed.

• 2.    Formulas for the approximate value of the first frequency were obtained by two analytical methods based on the inductive generalization of particular solutions. The results are compared with the numerical method. It is shown that the simplified Dunkerley method gives a simpler and more accurate solution, the error of which decreases with increasing number of panels.

• 3.    Spectral constants and resonance safety zones were discovered in the spectra of the family of regular trusses.

• 5 Fundings

  The work was carried out with the financial support of the Russian Science Foundation 22-2100473.