Formulas for calculating the deflection and displacement of a planar truss support with short studs in a lattice

The calculation of deformations of building structures is usually carried out by the finite element method in numerical form [1]–[3]. Analytical methods are used much less often in engineering calculations. For regular trusses with periodically repeating structures in the lattice, in [4]–[7], together with operators of computer mathematics systems, the method of induction is used, which makes it possible to derive calculation formulas for an arbitrary order of structure regularity. Problems of regular statically determinate rod systems were dealt with by Hutchinson, R.G. and Fleck, N.A. [8], [9]. Matrix methods and graph theory in the calculations of regular planar and spatial trusses in relation to their optimization were applied by Kaveh A. [10]–[12]. In the papers [13]–[18], by induction in the Maple system, solutions were obtained for the problems of deflection of various planar trusses with an arbitrary number of panels. An analytical estimate of the first natural frequency of oscillations of planar and spatial trusses was found in [19]–[21]. A two-sided estimate of the first frequency of a regular truss in an analytical form using the Maple system was obtained in [22]. The article [23] proposes a two-node method for predicting the effective elastic properties of a periodic cellular truss. The continuum representation for calculating a regular truss is used in [24]. In [25], in the problem of periodic truss networks based on the concepts of the quasi-continuum method, the decomposition of a regular truss lattice into simple Bravais lattices is used. To reduce computational costs while accurately taking into account the dominant deformation mechanisms, a homogenized continuum description of lattice trusses is introduced in [26], based on the application of the Cauchy–Born multilattice rule to a representative unit cell. The author's handbooks [27], [28] contain schemes of planar static determinate trusses and formulas for calculating their deflections and forces in characteristic rods. Analytical methods for calculating a regular truss in relation to the problem of optimization taking into account creep were also used in [29].

• 2    Materials and Methods

The truss consists of two shortened side panels and n panels in its middle part (Fig. 1). In addition to nodes in the upper and lower chords, the truss has nodes in the middle part, to which racks of height h are attached. The braces of the lattice are connected to the hinges of the truss belts and to the upper nodes of the racks. Thus, the rods of the upper chord, compressed under the action of a vertical load and allowing buckling, have a shorter length than the tension rods of the lower chord. This increases the local stability of the structure. The truss contains K = 8 n + 19 rods. The total length of all rods 4( n + 1) a + 10( n + 1) c + ( n + 7) h , where c = V a ² + h ² .

Fig. 1. Truss, n=6 . The uniform load on the lower chord.

Calculation of forces in the bars of a statically determinate truss is performed by the method of cutting nodes. Information about the truss scheme and coordinates of hinges and supports is entered into the program [30] parametrically for an arbitrary number of panels. Truss nodes are numbered, the origin is placed in the left support (Fig. 2).

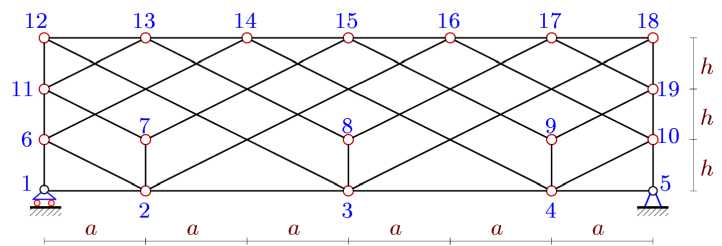
Fig. 2. Truss node numbering, n=2 .

The coordinates of the nodes in the Maple system are given in cycles, the length of which is determined by the parameter n:

> x[1]:=0:y[1]:=0:x[n+3]:=2*(n+1)*a:y[n+3]:=0:

> for i to n+1 do x[i+1]:=2*a*i-a; y[i+1]:=0; end:#bottom

> for i to n+3 do x[i+3+n]:=x[i]; y[i+3+n]:=h;end:#midle

> x[2*n+7]:=0:y[2*n+7]:=2*h:        #left

> x[4*n+11]:=x[n+3]:y[4*n+11]:=2*h: #right

• > for i to 2*n+3 do x[i+2*n+7]:=a*(i-1); y[i+2*n+7]:=3*h;end:#top

The structure of the lattice is determined by special lists N[i], i =1,.., K +3 of the ends of the bars, including three bars modeling supports. For the bars of the lower chord and racks, these lists look like:

• >    for i to n+2 do N[i]: = [i,i+1]; end:

• > for i to n+3 do N[i+n+2]:=[i,i+n+3]; end:

The calculation of forces in a number of trusses with a different number of panels revealed a feature of the proposed lattice scheme. It turns out that for some values n =1, 2, 3, 5, 7, 8, 9, 11, 13, 14, 15,... the determinant of the matrix of the system of equations vanishes. The picture of the distribution of possible node velocities, confirming this feature, was obtained by kinematics methods (Fig. 3). For n =1 nodes 1-5, 8, 10, 12, 14 remain motionless. The ratio of velocities is obvious: v / a = u I h . Some of the rods make an instant rotational movement, some — a planar one. Rods 9-6 and 7-15 acquire instantaneous translational motion. A similar picture of the distribution of possible node velocities can be obtained for other invalid truss orders. To eliminate these orders, we consider a sequence of trusses with n = (1 - ( - 1) k + 6 k )/2, k = 1,2,... .

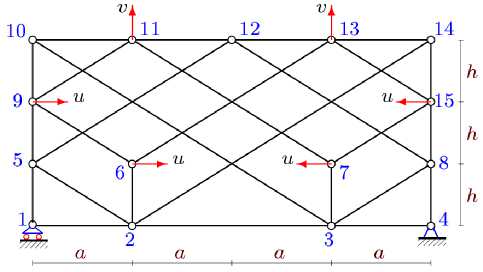
Fig. 3. Virtual velocities of variable truss nodes with n=1

• 3    Results and Discussion

  3.1    Calculation of forces

The system of equilibrium equations for nodes is written in matrix form GS = B . The even elements of the vector on the right side are filled with vertical loads on the nodes, and the odd elements are horizontal. The solution to the system of equations is found in the Maple system by the inverse matrix method S = G ^{- 1} B . The distribution of forces in the rods under the action of a load on the truss along the lower chord is shown in Figure 4. The values of the forces at P =1 are rounded to two significant figures. Compressed rods are highlighted in blue, stretched rods are highlighted in red. Unstressed bars are indicated by thin black lines. The thickness of the segments of the rods is conditionally proportional to the modules of the corresponding forces. It is characteristic that the most compressed rods of the upper chord are not located in the middle of the span.

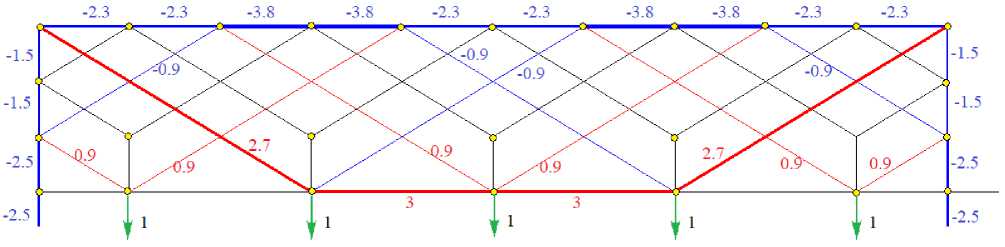
Fig. 4. Distribution of forces from the load on the lower belt, a = 3 m , h = 2 m

A similar picture of the distribution of forces in the rods in the case of a uniform nodal load on the upper chord is shown in Figure 5. Here, the most stretched bars of the lower chord are also not in the middle of the span, as expected. The rods of the upper belt along the edges of the truss are stretched.

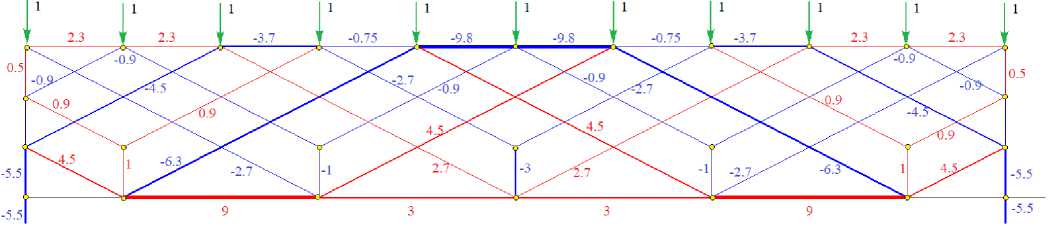
Fig. 5. Distribution of forces from the action of the load along the upper chord, a = 3 m , h = 2 m

For forces in the rods, the most critical to loss of stability or strength, analytical dependencies on the number of panels were obtained by induction.

From the calculations of a number of trusses in the symbolic form for force O 1 in the rod of the middle of the upper belt (Fig. 1), the sequence of values was obtained:

- 5 Pa /(2 h ), - 9 Pa /(2 h ), - 21 Pa /(2 h ), - 29 Pa /(2 h ), - 49 Pa /(2 h ),... .

The rgf_findrecur operator of the Maple system for members of this sequence gives a linear homogeneous recurrent equation of the fifth order

O i, k = O i, k - 1 + 2 O i, k - 2 - 2 O i, k - 3 - O i, k - 4 + O i, k - 5 .

The solution of the recurrent equation obtained using the rsolve operator is:

O _i = - Pa (6 k ² + 2(3 - ( - 1) ^k ) k - ( - 1) ^k + 5) / (8 h ).

Similarly, formulas for other forces are found:

O ₂ = - Pa (6 k ² + 2(3 - ( - 1) ^k ) k - ( - 1) ^k - 3) / (8 h ),

U ₁ = Pa (6 k ² + 2(3 - ( - 1) ^k ) k - 15 - ( - 1) ^k ) / (8 h ), U ₂ = Pa (6 k ² + 2(3 - ( - 1) ^k ) k + 1 - ( - 1) ^k ) / (8 h ).

The presence in these solutions of coefficients depending on the parity of k makes the dependences nonmonotonic as k changes. The height value h is in the denominators of the found functions, which indicates an increase in the forces in the rods of the upper and lower chords with a decrease in the height of the truss.

3.2    Structural deformations

To calculate the deflection, assuming that all elements of the truss experience only tension and compression, the Maxwell-Mohr formula is used in the form

^K                                                              (1)

A = z S a P ’ S S' l „ /( EF ).

a=1

Суммирование ведется по всем деформируемым стержням конструкции. Здесь обозначено: EF - жесткость стержней (одинаковая для всех стержней фермы) , l _a — the length of the rod, S a ¹ — the force in the rod number a from the action of a single vertical force applied to the point C , S a ^P ) — усилие в этом же стержне от действия внешней нагрузки. В сумму не входят три жестких стержня, моделирующие левую подвижную и правую неподвижную опоры.

Расчет прогиба от действия нагрузки, равномерно распределенной по узлам нижнего пояса показывает, что формула для прогиба имеет следующий вид:

Summation is carried out for all deformable rods of the structure. Here it is indicated: EF — the stiffness of the rods (the same for all truss rods), la — the length of the rod, S— the force in the rod number from the action of a single vertical force applied to the point C, S(aP) — the force in the same rod from the action of an external load. The sum does not include three rigid rods modeling the left movable and right fixed supports.

The calculation of deflection from the action of a load evenly distributed over the nodes of the lower belt shows that the formula for deflection has the following form:

A k = ( C 1 a ³ + C 2 c ³ + C ₃ h ³)/( h ² EF ), k = 1,2,...                          (2)

For k =1,..,18, the following expressions are obtained: A 1 = (13 a ³ - 9 c ³ - h ³)/(2 h ² EF ),

A ₂ = (121 a ³ + 27 c ³ + 5 h ³)/(2 h ² EF ), A ₃ = (637 a ³ - 9 c ³ + h ³)/(2 h ² EF ),

A 4 = (133 a ³ + 63 c ³ + 7 h ³)/(2 h ² EF ),...

A ₁₈ = (423433 a ³ + 651 c ³ + 21 h ³)/(2 h ² EF ).

Operators of the mathematical system of symbolic mathematics are used to find common terms of sequences of coefficients. In the Maple system for the sequence 13, 121, 637, 133, ..., 423433 coefficients C _{1, k} using the rgf_findrecur operator from the genfunc package, a homogeneous linear recurrence equation of the ninth order can be obtained:

C k = C k - 1 + 4 C k - 2 - 4 C 1, k — 3 - 6 C 1, k - 4 + 6 C 1, k - 5 + 4 C 1, k - 6 - 4 C 1, _k - 7 - C 1, _k - 8 + C 1, _k - 9 .

The solution of this equation gives the dependence of the coefficient at a ³ on k in the form of a fourth-order polynomial with coefficients having a sign depending on the parity of the number k :

C 1 = (30 k ⁴ + 20(3 - ( - 1) ^k ) k ³ + 6(7 - 5( - 1) ^k ) k ² + 4(11( - 1) ^k + 3) k + 27( - 1) ^k - 19)/16.      (4)

Here, to find the common term (4), it was necessary to obtain a sequence of solutions of length 18. With a shorter sequence length, the Maple system does not find a solution. It should be noted that the solution time of the system of linear equilibrium equations of large-order nodes in symbolic form is much longer than in numerical form. With increasing k , the calculation time of each subsequent truss increases noticeably. This is especially evident in the company under consideration, for which the sequence of allowable numbers n is sparse: n=4, 6,10,12,16,18, 22, 24, 28, 30, 34, 36, 40, 42, 46, 48, 52, 54.... At these values, the determinant does not vanish.

Similarly, but somewhat simpler, other coefficients in (2) are obtained:

C ₂ = 3(2 k ² + (10( - 1) ^k + 2) k + 5( - 1) ^k - 1) / 8,

C 3 = (5( - 1) ^k + 2 k + 1)/4.

3.3    Calculation of the support shift

The left movable hinge support under the action of a vertical load receives some displacement. It can be calculated using the Maxwell-Mohr formula (1), where S ® is the force from the action of a single horizontal force on this support. The result of the calculation for a different number of panels has the form:

§ _k = Pa ² D _k /( hEF ).

The sequence of coefficients D_k obtained from solving a number of trusses with the number of panels n=4, 6.10,..., 54 has the form: 8, 32, 136, 232, 528, 744, 1328, 1712, 2680, 3280, 4728, 5592, 7616, 8792. For this sequence, the rgf_findrecur operator returns the recurrent equation:

D k = D k - 1 + 3 D k - 2 - 3 D k - 3 - 3 D k - 4 + 3 D k - 5 + D k - 6 - D k - 7 .

The solution of the equation gives the desired dependence

(5) § _k = Pa ²(6 k ³ + 3(3 - ( - 1) ^k ) k ² - (3( - 1) ^k + 1) k + 2( - 1) ^k - 2)/(2 hEF ).

As in solution (2) with coefficients (3), (4), the result is affected by the parity of the number k characterizing the number of panels.

3.4    Numerical example

The obtained dependence of the deflection on the number of panels under the action of a nodal load on the lower belt on the truss is graphically displayed in Figure 6. The designation of dimensionless relative deflection К = EFК / ( P s L ) is introduced, where P s = Pn is the total vertical load on the structure, L = 2( n + 1) a = 150m is the length of the truss span. The change in the deflection in the accepted formulation with an increase in the number of panels is non-monotonic. The jumps in the magnitude of the relative deflection are significant at the beginning of the curve gradually decrease.

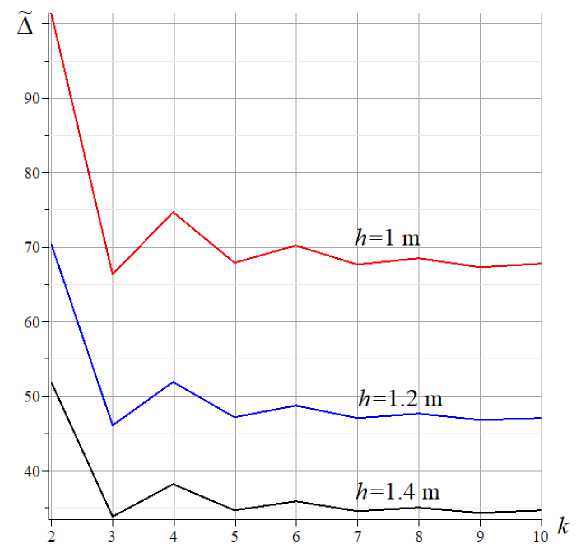
Fig. 6. The dependence of the relative deflection on the action of the load on the bottom chord on the number of panels

The same curves for the magnitude 5 = EF 5 / ( P s L ) of the relative horizontal shift of the support at L = 150m are shown in Figure 7. All curves have an implicitly expressed maximum, depending on the height of the truss, and horizontal asymptotes, the values of which are given by the limit operator of the Maple system: lim 5 = L /(36 h ). k ^^

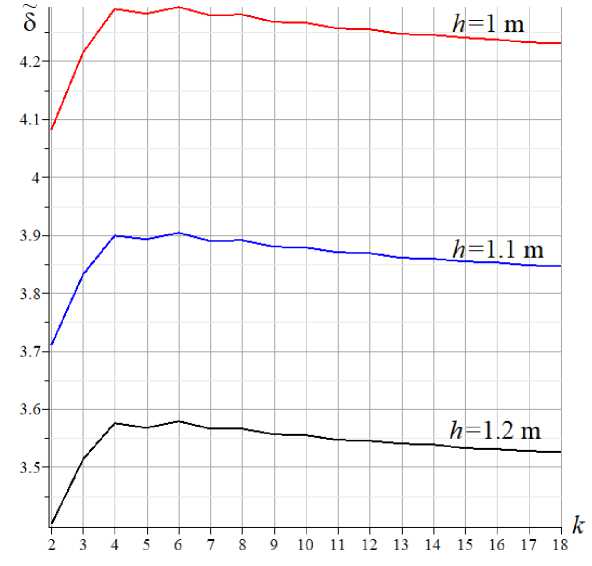
Fig. 7. The dependence of the shift of the movable support on the number of panels under the action of a distributed load on the lower belt

The increase in deflection and displacement of the support with a decrease in the height of the truss is quite predictable. Firstly, this also follows from the analytical solution, in which the height of the structure is in the denominator, and secondly, this corresponds to the physical representation of the work of the beam structure under the action of vertical forces. Thin beams bend more, and the displacement of the movable support is greater.

The curves in Figures 6 and 7 are not completely monotonic and contain local extrema. This is due to the presence of a complex lattice in the design of the truss. In simple triangular beam trusses, these curves are monotonic [7].

• 4    Conclusions

The main results of the work are as follows.

• 1.    A mathematical model of deformations of a new scheme of a planar statically determinate truss is constructed.

• 2.    The distribution of forces over the structure rods is shown, which reveals the most loaded rods.

• 3.    Cases of kinematic shape variability with a certain number of panels have been identified. A corresponding picture of the distribution of possible node speeds is constructed, confirming this case.

• 4.    Formulas of dependences of deflection, displacement of the support and forces in the rods on the number of panels are derived.

• 5 Acknowledgements

  This work was financially supported by the Russian Science Foundation 22-21-00473.