Формулировка метода конечных элементов с учетом сингулярности для плоской задачи смешанных форм разрушения
Автор: Тартыгашева А.М., Шлянников В.Н., Туманов А.В.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Целью данного исследования является формулировка варианта метода конечных элементов для плоской задачи смешанных форм деформирования и получение аналитического решения для коэффициентов матрицы жесткости для элементов области сингулярности с центром в вершине трещины. Объектом численного исследования являлась пластина условно бесконечных размеров со сквозной прямолинейной центральной трещиной при равнодвухосном растяжении в условиях плоской деформации. Проведен анализ особенностей распределения полей напряженно-деформированного состояния и коэффициентов интенсивности напряжений в области вершины трещины, определяемых с помощью метода конечных элементов с учетом сингулярности. Получены аналитические формулы задания кинематических условий для общего и частного случая нагружения пластины с дефектом в упругой постановке для случая плоской деформации. Представлен сравнительный анализ численных результатов для двух случаев формирования расчетной схемы вершины трещины: традиционным методом создания математического разреза и при помощи метода конечных элементов с учетом сингулярности. Установлено преимущество применения метода конечных элементов с учетом сингулярности. На примере пластины со сквозной прямолинейной центральной трещиной при равнодвухосном растяжении показано, что задание граничных условий в вершине трещины с учетом сингулярности позволяет существенно понизить размерность расчетной схемы метода конечных элементов без потери точности расчета. Сделан вывод о возможности применения подобной формулировки в упругопластической постановке. Тарировка полученного решения проводилась для полей напряженно-деформированного состояния и коэффициентов интенсивности напряжений, определенных с помощью классического метода конечных элементов и метода конечных элементов с учетом сингулярности.
Смешанные формы деформирования и разрушения, сингулярность в вершине трещины, коэффициенты матрицы жесткости, трещина, механика разрушения, метод конечных элементов
Короткий адрес: https://sciup.org/146282019
IDR: 146282019 | УДК: 539.42 | DOI: 10.15593/perm.mech/2020.4.19
Текст научной статьи Формулировка метода конечных элементов с учетом сингулярности для плоской задачи смешанных форм разрушения
The paper deals with obtaining an analytical solution for stiffness matrix coefficients at a crack tip area for mixed mode cracks in plane strain conditions. The numerical study is focused on an infinite plate with a straight-through central crack under mixed loading. Analytical solutions are obtained as kinematic boundary conditions for plane strain. We analyzed distribution features of the stress-strain state fields and stress intensity coefficients at the top of the crack area, determined using the finite element method taking into account the singularity. The analytical formulas are obtained which set the kinematic conditions for a general and special case of loading a plate with a defect in the elastic setting for the case of plane deformation. The comparative analysis of the numerical results is presented for two cases of forming the design diagram of the top of the crack: the traditional method of creating a mathematical cut and the finite element method taking into account the singularity. The advantage of using the finite element method considering the singularity is found. We used an example of a plate with a through straight rectilinear central crack with the equal biaxial tension to show that setting the boundary conditions at the top of the crack taking into account the singularity allows one to significantly reduce dimensions of a calculation scheme of the finite element method and keep the calculation accuracy. It is concluded that such a formulation can be applied in an elastic-plastic formulation. The comparison between the classical finite element solution and finite element with singularity is presented. The convenience of the finite element method with singular boundary conditions is demonstrated.
Во многих прикладных областях технических наук большое внимание уделяется математическому описанию процессов деформирования и разрушения материалов [6, 8–10, 25, 29, 39, 50, 56, 60, 65–67, 70]. Зависимость параметров напряженно-деформированного состояния макро- и микроуровня принято выражать с помощью введения последовательности окружностей различного радиуса вокруг вершины трещины. Выделенные зоны обладают различной сингулярностью поля напряжений. Явное внимание к данному вопросу видно из огромного количества работ российских и зарубежных ученых – исследований поведения различных материалов при всевозможных типах нагружения в упругой, упругопластической постановках и при ползучести.
Очень подробно асимптотические методы решения в нелинейной механике разрушения описаны в обзорных статьях Л.В. Степановой, Е.А. Адылиной и С.А. Игонина [31, 33]. В публикациях [19, 30] предложен метод численного определения собственных значений для всех значений параметра смешанности нагружения в нелинейной постановке в условиях ползучести для зон с различной особенностью поля напряжений. Показано приближенное решение для определения полей напряжений и скоростей деформаций ползучести вблизи вершины трещины при поперечном сдвиге. Установлено, что вблизи вершины трещины скорости деформаций имеют сингулярность, показатель которой меняется дискретно в зависимости от полярного угла. Численное моделирование скорости накопления деформаций и повреждений при ползучести с учетом особенностей в области поврежденности материала представлено в работах В.Н. Шлянникова, А.В. Туманова, Л.В. Степановой [38, 68]. Авторами В.А. Нифагиным, М.А. Гун-диной, В.Е. Паниным, М.Д. Моисеенко и т.д. [22, 23, 37] описано напряженно-деформированное состояние в окрестности вершины трещины в условиях пластичности, получена оценка напряженного состояния в области промежуточной структуры вершины трещины, показывающая значительное отличие роста размера зоны пластичности в зависимости от вида напряженного состояния. Представлена оценка влияния комплекса пластических свойств сталей на состояние в области вершины трещины при произвольном двухосном нагружении. Описан дискретно-континуальный метод моделирования напряженно-деформированного состояния в вершинах трещин и надрезах с учетом кривизны кристаллической решетки. Интересный результат получен в статье С.А. Назарова [21], после постепенного введения базисов сингулярных степенных решений вблизи вершины трещины и изучения их свойств установлено, что в случае вещественного показателя сингулярности напряжений базисы сохраняют свойства базисов для однородной среды. Нельзя не отметить исследования коллектива авторов Л.Р. Лапин, В.П. Матвеенко, А.Ю. Федоров, И.Н. Шардаков [16–18], в которых описаны новые алгоритмы для расчета напряжений в упругих телах с особыми точками и на основе метода конечных элементов с использованием построенных полу-аналитических сингулярных элементов проведен анализ полной энергии образцов с трещиной при различном расположении трещины в однородном и неоднородном образцах, а также в образцах с концентраторами напряжений.
Широкое распространение и ведущую роль при анализе напряженно-деформированного состояния конструкций сложной геометрии получил метод конечных элементов (МКЭ) [1–3, 13, 20, 27, 34, 35, 40, 55, 62–64, 69, 71–73, 75], о чем свидетельствует большое количество программных продуктов, реализующих этот метод. Однако применительно к задачам механики трещин существуют определенные сложности при использовании МКЭ. Известно, что сингулярное решение приводит к бесконечно высоким напряжениям в области вершины трещины [12, 26, 28, 74, 76, 77]. В этом случае в расчетной схеме МКЭ будет присутствовать как минимум четыре элемента, узлы которых будут принадлежать точке вершины трещины. В данных элементах точное решение не может быть получено, так как при нулевом радиусе кривизны вершины трещины определитель матрицы жесткости становится отрицательным. Следовательно, при моделировании области вершины трещины необходимо закладывать область выхода искомой функции на сходящееся решение, при этом размер области, исключаемой из рассмотрения ввиду присутствия в ней больших погрешностей, должен быть меньше области непосредственного анализа искомых функций. Данное обстоятельство приводит к существенному увеличению размерности общей матрицы жесткости, особенно в трехмерных задачах. Таким образом, основным недостатком прямых методов расчета параметров разрушения является недостаточная обоснованность смещений в вершине трещины.
В настоящее время существуют различные модификации метода конечных элементов. Одним из вариантов стало использование данного метода с внедрением «суперэлементов» [5, 7, 15, 45], расширенный метод конечных элементов, используемый для моделирования макро- и микротрещин описан в работах авторов [61, 51, 52, 54], с градиентно-взвешенным расширенным методом конечных элементов (GW-XFEM) для механики разрушения можно познакомиться в статье [44], метод конечных элементов совместно с методами цифровой фотоупругости рассмотрен в публикации [32]. Особенность моделирования пространственных трещин описана авторами [4, 11, 14, 46]. Исследователями M.M. Nojumi и X. Wang [57] предложен метод динамического анализа применительно к материалам с трещинами в трехмерной постановке с использованием нового градуированного сингулярного конечного элемента. Главным преимуществом предложенного элемента является отсутствие необходимости постобработки для расчета параметров разрушения. В работе [53] показано, что деформированные сингулярные элементы (моделирующие требуемый вид особенности путем сдвига промежуточных узлов на сторонах обычных элементов высокого порядка) дают лучшие результаты при описании особенности в окрестности вершины трещины, чем элементы, аппроксимирующие функции которых содержат члены из асимптотического решения в перемещениях.
Авторами P.D. Hilton и G.C. Sih [48] был предложен метод, позволяющий избежать ошибки, возникающей из-за невозможности описать аппроксимирующими функциями сингулярное решение. Сущность этого метода заключается в объединении метода конечных элементов и аналитических разложений в вершине трещины. Смысл такого подхода основан на математических свойствах двух используемых методов расчета: асимптотические разложение становится гораздо более точным при достижении области сингулярности (вершины трещины), тогда как МКЭ может быть точным везде, кроме области вершины трещины. Эти два метода объединены так, что каждый используется в той области, где он дает наибольшую точность, и не используется там, где его точность становится сомнительной. Данный обобщенный метод является наиболее предпочтительным для анализа сопротивления разрушению различных конструкций, находящихся в условиях плоского напряженного состояния ввиду его строгой математической и физической обоснованности.
Эти соображения привели P.D. Hilton и G.C. Sih к созданию специального МКЭ для изучения поведения трещин, в котором для элемента сетки, совпадающего с вершиной трещины, используется асимптотическое разложение. Метод, предложенный P.D. Hilton и G.C. Sih, был разработан для частного случая плоского напряженного состояния. В основу рассмотрения положен вариационный принцип нахождения минимума потенциальной энергии. Вся конструкция разбивается на две области с помощью дуги окружности с центром в вершине трещины. Потенциальная энергия деформации определяется отдельно для каждой области. Для области, ограниченной окружностью, потенциальная энергия ищется с использованием асимптотического разложения, а вне этой области, разбитой на конечные элементы, энергия деформации вычисляется стандартным способом. Для узлов сетки конечных элементов, расположенных на дуге окружности, должно выполняться условие, чтобы смещения в них совпадали со смещениями, определяемыми с помощью асимптотического разложения. Таким образом, аналитически вычисленные перемещения включены как граничные условия в численное решение, тем самым непрерывность перемещений обеспечена в узлах на границе круговой области.
Метод, предложенный P.D. Hilton и G.C. Sih, был разработан для частного случая плоского напряженного состояния. Целью данной работы является формулировка подобного метода для общей плоской задачи смешанных форм деформирования и получение аналитического решения для коэффициентов матрицы жесткости элементов, граничащих с областью сингулярности для общего случая двухосного нагружения прямо- линейной наклонной трещины. В связи с тем, что при критериальных оценках прочности необходимо знание точных параметров НДС на конкретных контурах вокруг вершины трещины, эти контуры должны быть правильно определены. В реальности приходится сталкиваться с противоречивой закономерностью: малая погрешность в вычислении контура может привести к большой погрешности в прочностных оценках конструкции. Поэтому возникла острая необходимость в точном установлении положения вершины трещины в нагруженной пластине, чтобы правильно определить контур для снятия результатов.
° yy
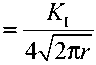
c 0 5 0
5cos—cos— 22
K II 472 П Г
■ 0 .50
sin--sin — 22
; (1)
K Г . 0 , .501 , K L 0 ,501
т =sin— + sin+I3cos— + cos; xy 4Т2ПГL 2 2J 472ПГL 22
kF 0 г i^ . 201, ux = — J—cos(x-1) + sin — + x G 2 2k 2L22
K • 0 Г 1, „
+ sin(x + 1) + cos
G 2 2k 2 L 2 2 J (2)
+°(-—Л ) { r [ cos( 0 + 2 a ) + x cos( 0 - 2 a ) - 8 G
- 2sin 0 sin 2 a ] + ( x + 1) a cos 2 a } + 5 1 ;
Рассмотрим пластину произвольной геометрии, находящуюся в условиях обобщенного плоского напряженного состояния или плоской деформации с прямолинейной наклонной трещиной (рис. 1). Начало полярных координат поместим в вершину трещины.
В работах J. Eftis, N. Subramoian и H. Libowitz [41–43] показано, что используемое ранее однопараметрическое асимптотическое представление напряжений и смещений у вершины трещины [24] не является адекватным. Причина этого связана с произвольным отбрасыванием в разложении напряжений по собственным функциям Вильямса второго члена, вклад которого не зависит от расстояния до вершины трещины.
kF ■ 0 г2 и = sin(x +1) - cos + y G 2 2k 2 L 22
K F 0 г 1Л ч . 2 01
+ — d —cos--(1 -x ) + sin2- +
G 2 2k 2 L 22
+—— — { r [ sin(2 a - 0 ) + x sin( 0 + 2 a ) - 8 G
- 2sin 0 cos 2 a ] + ( x + 1) a sin 2 a } + 3 2,
σ
А А A A A A A A A
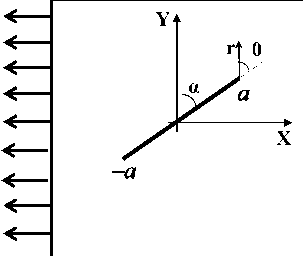
Рис. 1. Пластина с наклонной прямой трещиной в поле двухосных напряжений
где r , 0 - полярные координаты, связанные с вершиной трещины; П — коэффициент двухосности номинальных напряжений; G - модуль сдвига; a - угол ориентации трещины относительно приложенных напряжений о ; x - константа, зависящая от коэффициента Пуассона v и равная (3 -v )/(1 + v ) и (3 - 4 v ) при плоском напряженном состоянии и плоской деформации соответственно; a – полудлина трещины.
Как требует метод P.D. Hilton и G.C. Sih, разобьем пластину на две области с помощью дуги Г радиусом R с центром в вершине трещины. Задача состоит в определении энергии деформации в области, ограниченной дугой Г радиусом R (рис. 2).
Fig. 1. Plate with an inclined crack under biaxial loading
В рамках плоской задачи линейной теории упругости для случая произвольной ориентации трещины при двухосном нагружении в соответствии с работами [41–43] при удержании двух членов разложения новые выражения для компонент тензора напряжений и смещений в области вершины трещины будут иметь следующий вид:
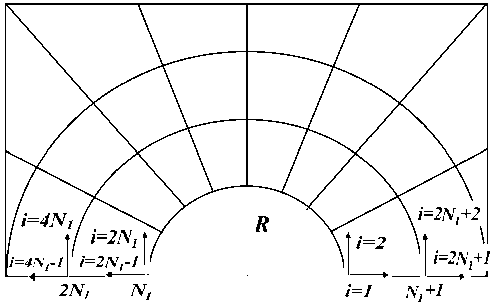
Рис. 2. Разбиение тела на области в соответствии c асимптотическим МКЭ с учетом сингулярности
о
xx
K . 6^ 50
—r-I— 3cos — + cos—
4 v 2 n r L 2 2 .
Fig. 2. Finite element model near the crack tip with taking into account the singularity
K II 4^2 к r
0 , .50 7sin — + sin —
+ о (1 -n )cos2 a ;
Для плоской задачи плотность потенциальной энергии упругодеформированного тела на единицу объема в любой точке определяется следующим образом [43]:
Ф( r , θ ) = 12 σ ij ε ij =
∂u x x∂x
∂ uy ∂ y
дur Г дu, duy xx+y д x ( ду дx
Для вычисления Ф( r , θ ) в области вершины трещины для задачи в соответствии с рис. 1 используем уравнения (1) и (2) вместе с соотношениями, приведенными в работе [43]:
В результате имеем:
in θ+
∂ u cos θ x
∂θ
-
r
;
∂ uy sin θ
∂θ r
.
K2
Ф( r , θ) = I [ (2χ-1)+2(χ-1)cosθ-cos2θ ] +
32 G π r
K2
+ II [ (2χ+3)+2(1-χ)cosθ+3,25cos2θ-0,25cos3θ ] + 32 G π r
KK K σ(1 -η)
+ III (1-χ)sinθ+sin2θ+ I
8 G π r [ ] 8 G 2π r
Гл.. 9.591
х (2х- 3)cos2 + cos "2 cos2a +
K I σ(1-η)(χ-1)
32 G 2π r
■ 959
-sin +sin sin 2α
-
K II σ(1 -η)
. 9 . 59
(2х + 1)sin2 + s |n^ cos 2а +
8 G V2n T L
K и о(1 -П )( Х- 1) "
32 g 72П Г l
+ σ 2(1 -η ) 16 G
з 9 59 .,
3cos +cos sin2α+
( χ+ 1) cos2 2 α .
Это выражение получено в работе автора [36]. Несколько иное по виду, но аналогичное по смыслу уравнение для Ф( r , θ ) приведено в работе J. Eftis, N. Subra-moian и H. Libowitz [43]. Входящие в уравнение (5) коэффициенты интенсивности напряжений K I и K II определяются по формулам:
K I =
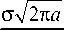
[ (1 +η ) - (1 -η )cos2 α ] ;
σ 2 π a
K II = 2 (1 -η ) sin2 α .
(5’)
Упругая энергия VC , накапливаемая в единице толщины круговой области радиусом R , около вершины трещины может быть получена в результате двукратного интегрирования выражения для плотности потенциальной энергии [36]:
K 2 R
I (2 χ- 1) + 32 G
V C = j j Ф( r , 9 ) rd 9 dr =
K 2 R
+ II (2 χ+ 3) + K I K II R (1 -χ ) + 32 G 4 G π
K σ (1 -η ) R3/2 K σ (1 -η ) R3/2
+ I(5 χ- 7)cos2 α+ I × 15 G 2 π 30 G 2 π
K σ (1 -η ) R3/2
× (1 -χ )sin2 α- II (5 χ+ 3)cos2 α+
15 G 2 π
+ K II σ (1 -η )R3/2(2 χ- 2)sin2 α+
30 G 2 π
+ σ 2(1 -η )2R2( χ+ 1)cos22 α . (6)
Согласно теории МКЭ с учетом сингулярности [47] алгоритм расчета параметров трещиностойкости состоит в определении потенциальной энергии в области вершины трещины с использованием асимптотического разложения и в определении потенциальной энергии области, исключающей сингулярность.
N
V = V C + Z V (r) - j (T ; u x - T n u у ) ds , (7)
r=1 S где V – полная потенциальная энергия тела; VC – полная потенциальная энергия области, ограниченной окружностью; V (r) – потенциальная энергия элемента сетки КЭ; Txn и Tyn – компоненты граничных сил на площадке s с нормалью n . Первый член выражения (7) определяется (6), а второй член получается стандартным способом по МКЭ и имеет вид
N N g N g
Z V (r) = ZZ K j UU j , r =1 i =1 j =1
где Kij – компоненты матрицы жесткости; ui , uj – смещения по единой нумерации узлов сетки; Ng – число степеней свободы, на которые не наложено ограничений. Минимизация полной потенциальной энергии (уравнение (7) относительно неизвестных параметров K I , K II , δ 1 , δ 2 и ui + 2 N 1 - 4) приводит к следующей системе линейных алгебраических уравнений:
∂ V
= K 11 KI + K 12 K II + K 13 δ 1 +
∂ K I
2 N 1 +4
+ K 14 8 2 + Z K i juj +2 N 1 -4 + B i = 0;
j =5
∂ V
= KK + KK + K δ+
21I22II231
∂ K II
2 N 1 +4
-
+ K 24 ^ 2 + Z K2 J u J +2 N i -4 + B2 = 0
j =5
= KK + KK + K δ+
∂δ 31 I 32 II 33 1
2 N 1 +4
-
+ K 34 8 2 + Z K 3 J u j +2 N 1 -4 + B 3 = 0;
j =5
∂ V
= K 41 K I + K 42 K II + K 43 δ 1 + K 44 δ 2 +
∂δ 2
2 N 1 + 4
+ £ K 4j u j + 2 n 1 -4 + B 4 = 0;
j =5
∂ VC ∂ K I
KR KR
= K I R (2 χ- 1) + K II R (1 -χ ) +
16 G 4 G π
σ (1 -η ) R3/2
15 G 2 π
× (5 χ- 7)cos2 α+σ (1 - η )R (1 -χ ) sin2 α ; (12)
30 G 2 π
=KK+KK+Kδ+ i1I i2II i31
∂ u i +2 N 1-4
Ng -2 N 1+4
+ Ki4 5 2 + £ Kij u j + 2 N 1 -4 + B i = 0;
j =5
∂ V KR K R
C = I(1 -χ ) + II(2 χ+ 3)
дКй 4Gk к I6G
-
σ (1 -η ) R3/2
15 G 2 π
σ (1 -η ) R3/2
× (5 χ+ 3)cos2 α+ 2( χ- 1) sin2 α ;
15 G 2 π
где K I и K II – коэффициенты интенсивности напряжений; δ 1 и δ 2 – проекции смещения вершины трещины на координатные оси; u j + 2 N 1 - 4 – перемещения узлов сетки КЭ; N 1 – число узлов на дуге Г.
Таким образом, задача сводится к добавлению четырех уравнений к стандартной системе уравнений МКЭ и формированию новой матрицы жесткости системы. Основную трудность при формировании системы (9) представляет определение компонент главной матрицы жесткости (за исключением Kij , которые определяются традиционным способом).
В связи с этим рассмотрим порядок вычисления компонент главной матрицы жесткости системы (9). Принятые обозначения приведены на рис. 2.
Полную потенциальную энергию представим в виде [24]
V = AK 2 + £ BK + ££ C j u i u j + ^ Du. (10) j
Здесь A – коэффициенты, содержащие вклады от области, ограниченной окружностью, и от узлов находящихся в первом полукольце; B – коэффициенты, описывающие связь между узлами первого и второго колец посредством элементов первого полукольца; C j и D – коэффициенты, соответственно связанные с узлами за первым полукольцом и с граничными условиями для нагрузок.
Введенные в (9) уравнения учитывают тот факт, что потенциальная энергия имеет минимум по неизвестным параметрам и представлена в виде (10).
В соответствии с нумерацией узлов и степеней свободы, показанных на рис. 2, для формул (2) с учетом (8) примем такое обозначение:
u = ( ux ) ( + 1) – – нечетное;
uj = ( ux ) ( j + 1) – j – нечетное; (11) 2
u = ( uy ) – – четное; uj = ( uy ) j – j – четное. 22
Частные производные от энергии деформации области, ограниченной окружностью VC (6), и от смещений (2), запишем в виде:
∂ ux = R 1/2
∂ K I G 2 π
e i n• 2 e cos2 2( x - 1) + sin 2 ;
;
|
∂ u R 1/2 θ |
Г1 z 2 e |
|
|
x = sin |
( χ+ 1) + cos2 |
; (12’) |
|
∂ K II G 2 π 2 |
L 2 2 _ |
|
|
∂ uy R 1/2 θ = sin |
1/ 291 ( χ+ 1) - cos2 |
; |
|
9 K i G 72 л 2 |
2 2 J |
|
|
∂ uy R 1/2 θ = cos |
Г 1л 4 -29 " (1 -χ ) + sin2 |
|
|
∂ K II G 2 π 2 |
L 2 2 _ |
На основании этого уравнения (9) можно перепи-
сать следующим образом:
∂ V ∂ K I
∂ V ∂ V NgNg ∂ u
= C + K u ;
9 к ii 9 к ii : : j 9 к ii j
N g N g
∂V = K d5, :: i
∂u i ij ∂δ1uj ;
g N g
∂ V = K d§ 2 :: i
∂ V
∂ u i +2 N 1-4
=1 j =1
∂u i ij ∂δ2 uj ;
=:: кУ1- i=1 j=1 ∂ui
∂ u i u j , i +2 N 1-4
1 - i - нечетное
где
d V a
= 0 - i - четное , i ≤ 2 N
95 1 ’ , 1
0 - i - четное , i > 2 N 1 , 0 - i - нечетное
д V 1 -
= 1 - i - четное , i ≤ 2 N
95 2 ’ , 1
0 - i - четное , i > 2 N 1.
После подстановки (2) в (13) с учетом (14), группируя члены относительно неизвестных параметров K I , K II , δ 1 , δ 2 и uj + 2 N 1 - 4 в каждом из уравнений системы (9), можно получить выражения для коэффициентов Kij и Bi в общем виде (15) – см. прил. 1.
В формулы (15) входят в явном виде угол ориентации трещины и коэффициент двухосности напряжений.
Численная процедура реализации данного алгоритма будет заключаться в вычислении матрицы жесткости элементов, находящихся между первым и вторым полукольцом (рис. 2), в расчете уточненных компонент главной матрицы жесткости с учетом дзухосности нагружения и угла ориентации трещины (по формулам (15)), в формировании новой главной матрицы жесткости системы и в решении самой системы линейных алгебраических уравнений (9) путем минимизации потенциальной энергии относительно неизвестных параметров .
Основное преимущество метода заключается в том, что его легко можно приспособить для имеющегося уже банка данных расчетных схем элементов конструкций. Для этого необходимо в ту или иную расчетную схему ввести разрез с круговой полостью на конце, где область, ограниченная дугой окружности с присущими ей специфическими характеристиками, выступает как некая подконструкция или суперэлемент. Причем характеристики этой области могут быть вычислены заранее по формулам (15). Кроме того, по сравнению с энергетическими методами конечных элементов, используемыми в механике разрушения, данный метод позволяет вместе с силовыми параметрами разрушения вычислить поля перемещений, деформаций и напряжений в области вершины трещины.
Точность самого метода конечных элементов с учетом сингулярности тщательным образом оценена его авторами P.D. Hilton и G.C. Sih на тестовых примерах. Отметим, что для случая одноосного растяжения и ан-типлоского сдвига этот метод имеет наибольшую точность по сравнению с другим известными методами. Однако кроме неоспоримых преимуществ асимптотический МКЭ с учетом сингулярности обладает следующими недостатками:
-
– недостаточная обоснованность метода для объемных задач;
-
– трудность учета криволинейности траектории развития трещины;
– необходимость дополнительной программы по вычислению уточненных компонент главной матрицы жесткости системы.
-
2. Аналитическое решение для частного случая равнодвухосного растяжения
Рассмотрим частный случай общего вывода смешанных форм разрушения применительно к ситуации равнодвухосного растяжения, при этом компоненты K II и 8 2 будут равны нулю, а коэффициент двухосности номинальных напряжений имеет конкретное значение п = 1.
В этом случае основные компоненты НДС (1)–(2) упрощаются к виду:
К, Г_ 9 5 91
о = —3cos- + cos— ;
4^ЛГ L 2 2 J
° yy
K I 4V2 n r
, 9
5cos
5 9 cos
K Г ■ 9 . .591 т„ = sin — + sin— ; xy 4x2nr L 22 ux = K ar^c cos9 Г i(%-1)+sin291+8i;
G 2 2K 2 L 22
KF е г u
U„ = Sin(X +1) - cos.
y G 22л 2 L 22
Плотность потенциальной энергии упругодеформи-рованного тела на единицу объема в этом случае тоже перепишем:
K 2
Ф( r , 9 ) = -4- [ (2 % - 1) + 2( x - 1) cos 9 - cos 2 9 ] . (18) 32 G л r
Входящий в уравнения (16)–(18) коэффициент интенсивности напряжений K I определяется по формуле
K I = о V 2n a .
В результате упругая энергия, накапливаемая в единице толщины круговой области радиусом R около вершины трещины, может быть получена по формуле
n R К 2 R
V c = J J Ф ( r , 9 ) rd 9 dr = -I - (2 / - 1). (20)
00 32 G
В системе (9) при минимизация полной потенциальной энергии, с учетом (18)–(20), останется только три уравнения из пяти:
2 N , +4
-- = KК I + К ,з 8 , + £ К ^ U j + 2N 1 -4 + B = 0;
д K j =5
2 N 1 + 4
= К 31 К I + К 33 8 1 + ^ К 3j U j + 2 N 1 -4 + В з = 0 ; (21)
d8 1 j =5
d V N g - 2 N - + 4
-------= Ki1KI + Ki381 + ^ Kjj N1 -4 + Bi = 0, d ui+2 N1 -4 j=5
где К I - коэффициент интенсивности напряжений; 8, -проекция смещения вершины трещины на координатную ось Ox ; U j + 2 N - 4 - перемещения узлов сетки КЭ; N 1 – число узлов на дуге Г.
Частные производные от энергии деформации области, ограниченной окружностью VC (20), и от смещений (17) запишем в виде:
d V C д К^
= K I R (2 Х- 1);
16 G
д и R 1 / 2 9
-- = ;= cos — д К i G 72л 2
2( х - 1) + sin 2
∂ uy ∂ KI
R 1/2 θ
sin
G 2 π 2
1 θ
2( χ+ 1) - cos2 2
С использованием полученных в п. 1 соотношений (13) и приведенных выше систем уравнений (17), (21)–(22), новые компоненты матрицы жесткости (23) для равнодвухосного растяжения приведены в прил. 2.
Штриховой линией показаны перемещения, рассчитанные аналитически по формуле (17). Точками показаны перемещения, полученные в результате численного расчета пластины, содержащей трещину в виде математического разреза. Разница представленных распределений может быть обусловлена фиксированными значениями коэффициентов интенсивности напряжений в аналитических расчетах.
-
3. Численная реализация для частного случая равнодвухосного растяжения
-
4. Результаты и обсуждение
Верификация предложенной формулировки МКЭ с учетом сингулярности проводилась для частного случая равнодвухосного растяжения пластины с центральной сквозной трещиной с использованием вычислительного комплекса ANSYS. Пластина находится в условиях равнодвухосного растяжения. Номинальные напряжения, приложенные к удаленным граням пластины, приняты равными 100 МПа. Для исключения влияния внешних граней пластины на область в вершине трещины ее ширина была принята равной 1 м. В результате для условий плоской деформации сформированы две расчетные схемы, отличающиеся между собой лишь способом моделирования вершины трещины.
В первой расчетной схеме моделировалась пластина условно бесконечных размеров, содержащая трещину длиной 5 мм в виде математического разреза. Минимальный размер элемента в области вершины трещины для данной расчетной схемы составил 1 мкм. Использовались 20-узловые конечные элементы второго порядка, при этом сингулярный элемент действительно не встраивается в конечно-элементную модель, а заменяется приложением перемещений, рассчитанных аналитически. Параметр δ 1 вычисляется из численного решения для пластины с математическим разрезом.
Вторая расчетная схема отличалась от первой только тем, что в области вершины трещины была исключена собственно вершина трещины и введена круговая полость как окружность радиусом 50 мкм. Рассчитанные аналитически перемещения задавались в качестве граничных условий в узлах на контуре круговой области. Заметим, что координата вершины трещины в виде математического разреза и центр окружности совпадали для обеих расчетных схем МКЭ.
Сравнение численных результатов для одной и той же пластины, при двух отличающихся между собой способах моделирования области сингулярности в вершине трещины, проводилось по двум маркерам. Во-первых, сопоставлялись поля напряженно-деформированного состояния, и во-вторых, анализировалось поведение коэффициентов интенсивности напряжений.
На рис. 3 представлено сравнение перемещений в области вершины трещины на контуре радиусом 50 мкм.
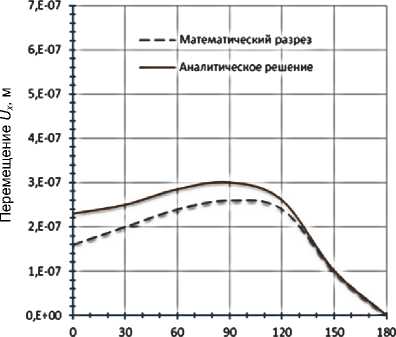
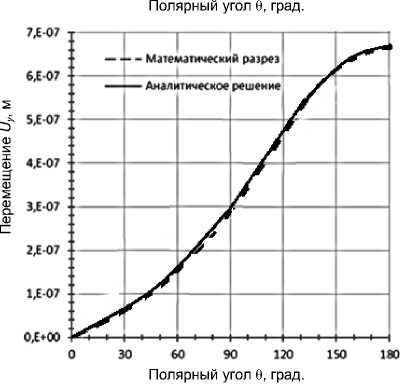
Рис. 3. Перемещения в области вершины трещины на контуре радиусом 50 мкм
Fig. 3. Displacements near the crack tip with a radius of 50 mm
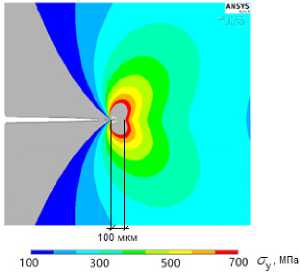
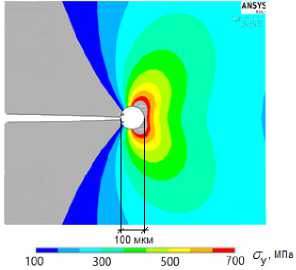
На рис. 4 представлены результаты расчета полей напряженно-деформированного состояния в области вершины трещины для случаев моделирования трещины в виде математического разреза (рис. 4, а ) и круговой полости с заданными граничными перемещениями в соответствии с методом конечных элементов с учетом сингулярности (рис. 4, б ). Из полученных данных следует, что стандартное моделирование вершины трещины и моделирование с исключением области сингулярности дают совпадающие результаты в широком диапазоне расстояний от вершины трещины. Данное обстоятельство свидетельствует в пользу предлагаемой в настоящей работе формулировки, так как в этом случае отсутствуют ограничения сходимости результатов вблизи области, окружающей вершину трещины.
б
Рис. 4. Сравнение полей напряженно-деформированного состояния трещины
Fig. 4. Comparison of stress-strain fields near the crack tip
Абсолютные значения компонент напряжений на продолжении трещины совпадают в сравниваемых вариантах расчетных схем МКЭ. Незначительные отличия наблюдаются только непосредственно на контуре, граничащем с исключаемой областью, но при малом удалении от данного контура к границам пластины разница в распределении полей напряженно-деформированного состояния исчезает (рис. 5).
Для пластины с трещиной в виде математического надреза теоретическое значение упругого коэффициента интенсивности напряжений KI составляет 12 МПа м при заданных условиях двухосного нагружения. Для задачи с круговой полостью, охватывающей вершину трещины с заданными кинематическими граничными условиями по периметру контура отверстия, величина упругого коэффициента интенсивности напряжений KI равна 18 МПа м . Это различие обусловлено тем, что в разрешающую систему МКЭ введено в качестве дополнительного параметра наряду с самим искомым КИН приращение длины трещины, которое имеет физический смысл размера зоны процесса разрушения. Кратко процедуру получения KI можно описать следующим образом. Параметры НДС и смещение δ1 вершины трещины получены численно для пластины с математическим разрезом при фиксированном уровне приложенных нагрузок, при которых KI составляет 12 МПа м . Следующим шагом является подстановка смещения δ1 в аналитический расчет, из которого определяем реальный коэффициент интенсивности напряжений KI, равный 18 МПа м, который используем для определения значения нагрузки при численных расчетах пластины с вершиной трещины в виде круговой области.
Данный результат в рамках упругой задачи свидетельствует в пользу предлагаемой формулировки МКЭ с учетом сингулярности.
Таким образом, на примере пластины при равнодвухосном растяжении показано, что задание граничных условий в вершине трещины с учетом сингулярности позволяет существенно понизить размерность расчетной схемы без потери точности расчета. Более того, данный метод обеспечивает более высокую степень сходимости результатов и позволяет решать задачи, в которых получение сходящегося решения при моделировании математического разреза невозможно. Особенно это актуально для полноразмерных трехмерных задач о поверхностных и внутренних трещинах, где уменьшение минимального размера элемента вдоль криволинейного фронта трещины ведет к экспоненциальному росту количества уравнений глобальной матрицы жесткости.
---МКЭ с учетом сингулярности
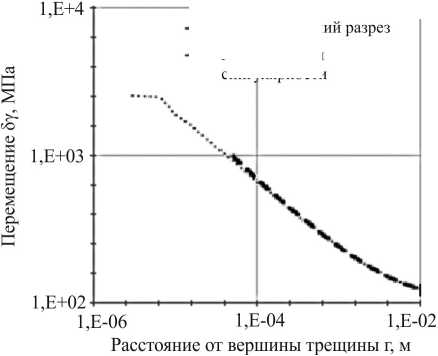
Рис. 5. Распределение напряжений на удалении от вершины трещины
Fig. 5. Distribution of stresses far from the crack tip
Одним из следующих этапов развития представленных в данной работе методов авторы видят получение коэффициентов матрицы жесткости позволяющих учесть зону пластических деформаций в области вершины трещины. Данная формулировка может быть использована для материалов, проявляющих свойства пластичности, если граничные условия будут заданы на основе решения Хатчинсона-Розенгрена-Райса [49, 50, 58, 59].
Представлена формулировка варианта МКЭ с учетом сингулярности для плоской задачи смешанных форм разрушения наклонной трещины при двухосном растяжении произвольного направления. Полученное аналитическое решение позволяет исключить сингулярность из расчетной схемы метода конечных элементов путем задания кинематических граничных условий на контуре вокруг вершины трещины. В качестве обоснования предлагаемого метода представлено сравнение
численных результатов для двух случаев формирования расчетной схемы вершины трещины. Показаны преимущества МКЭ с учетом сингулярности по отношению к традиционному методу моделирования трещины в виде математического разреза.
основе сплайн-вейвлетов // Фундаментальные, поисковые и прикладные исследования Российской академии архитектуры и строительных наук по научному обеспечению развития архитектуры, градостроительства и строительной отрасли Российской Федерации в 2018 году. – 2019. – С. 249–260.
1. Zhang R., Guo R. Determination of crack tip stress intensity factors by singular Voronoi cell finite element model. Engineering Fracture Mechanics , 2018, no. 197, pp: 206-216.
K 1
= R (2x-1)
16 G
” 2 N ] - 1 2 N ] - 1
E E K ij cos
0 ( ' +1)/2 cos0 (j - '’ 2
R
+
2 G 2 n
K 12
i = 1,3 j = 1,3
2 N ] - 1 2 N ।
+ E E K ij cos
i = 1,3 j = 2,4
2 N . 2 N 1 - 1 a
EE K j sin > i = 2,4 j = 1,3 2
0 (i + 1)/2
1 ( x-1 ) + s'n 2
sin j 2 ( x-1 ) + sin 2
0 (i + 1)/2
- x 2 ( x- 1 ) + sin 2 ^у 2 x [ 2 (x+1)- cos2 02 2 ]+
+
0 (j + 1)/2 cos
2 ( x+1 ) -cos 2 ”^
2 N 2 N , 0
+ EE K ij sin^si
i = 2,4 j = 2,4
= R (1 -x) +
4 G n
' 2 N j - 1 2 N j - 1
E E K j cos
sin j 2 ( x +1 ) -cos 2 02 2 x
0 (' + 1)'2 sin 0 (* + 1)'2
R
+--7---'
2 G 2 n
i = 1,3 j = 1,3
2 N ] - 1 2 N ]
+ E E K ij cos
0 (i + 1)/2
2 ( x- 1 ) + sin 2
i = 1,3 J = 2,4
2 N , 2 N 1 - 1 a
E E Ku s'n^s'n i = 2,4 J = 1,3 2
0„ 1
cos^” 2 ( x - 1 ) + si n
0 (j + 1)/2 2
2 N 1 2 N 1 a
+ EE K j sin 0 /2 i = 2,4 i 2 I 2
K 13
x 2 ( x-1 ) + sin 2 -(y1■ ; 2 ( x + 1 ) -cos 2 j
; 0(i + 1)/2 2
0 (i + 1)/2
2 ( X + 1 ) - cos2 0 2
cos j- 1 ( x +1 ) -cos 202 2 2V ’ 2
>
+
x 2 ( x + 1 ) + cos2 -jr 2
x [ 2 ( 1 -x) +-2 ]+
> [ 2-' 1 ) + cos ' j2 x 2 ( x+1 ) +sin 2 ”2 il
+
+
•
;
_
GN 2n
K 4 = Ш
- =1 f R 1 j G \ 2n
2 N। -12 N। -1
E E Kj cos i=1 3 i=13
2 N 1 2 N 1 - 1 a
+ EE Ky sin0 /2
i = 2.4 i = 13 2
2 N ] - 1 2 N ।
E E K ij cos
2 N 1 2 N 1
2 ( x-1 ) + s'n2 fel
2 ( x+1 ) -cos 2 ° 22
0 (i + 1)/2
2 ( x-1 ) +sin 2 ” ■
;
+ EE K j sin 0 2 i = 2 4 i = 2 4 2
2 ( x + 1 ) - cos 2 'v
;
2 N 1 -1 A
Ет.л V (i+1)/2
Ki -, j -+2 N 1 -4 cos— i =1 3 2
2 ( x- 1 ) + sin2 ^
2 N 1
+ E K j2N 1 -4
0 i
s'nT 2 ( x + 1 ) - cos2 ^
^ , j = 5,6...2 N 1 + 4;
B = a(1 -n) R 1/2 1 8 G V2n
-1 R [ ( 5x- 7 ) cos2a + 0,5(1 -x)sin2a ] +
2 N , - 1 2 N j - 1
E E K ij cos
+1 - G
i = 1,3 j = 1,3
2 N । - 1 2 N ।
+ E E Kij cos i=1,3 j=2,4
2 N । 2 N ] - 1 ,
0 ( i + 1)/2 2
1 ( x-1 ) + sin2 fel
0 ( i + 1)/2 2
+ EE Kj sin °2 ;
i = 2,4 j = 1,3
2 N 1 2 N 1
+ E E Kj sin ”1/r i = 2,4 j = 2,4 2
2 ( x-1 ) + sin 2 ”1 2 111
2 ( x+1 ) -cos 2 0 22
2 ( x+ 1 ) - cos 2 0 22
R (cos( 0 ( j + 1)/2 + 2 a ) + x cos( 0 ( j + 1)/2 - 2 a ) -2sin 2a sin 0 ( j + 1)/2 + (x +1) a cos 2a
R (sin(2a - 0 j /2 ) + x sin(2a + 0 j /2 ) --2 cos 2a sin 0 j /2 + (x +1) a sin 2a
"R (cos(0 ( j +n/2 + 2a) + x cos(0 ( j ^ - 2a) -2sin 2a sin 0Q+ 1)/2 + (x +1) a cos 2a R (sin(2a - 0 ( j +n/2 ) + x sin(2a + 0 j /2 ) --2 cos 2a sin 0 j/2 + (x +1) a sin 2a
+
+
+
(;
>
' 2 N 1 -1 2 N 1 -1
S S K sin
+--2—3
2 G 2 n
K R (2 x + 3)
K 22 = “16 G-
6 (i+1)/2 sin 6 (j+1)/2
2 N 1 -1 2 N
+ S S K j sin
i =1,3 j =2,4
2 N 1 2 N 1 -1
6 j +1)/2
S S K co 6 /2 sin
i =2,4 j =1,3
2 N 1 2 N 1
+ SS K ij Cos^
i =2,4 j =2,4
K 23 =
K 24 =
2N N -1
2 ( X + 1 ) + cos2
6 ; , 2 I , cos-2- 2 ( x + 1 ) + cos2
6 (j+1)/2
= 5
2 j G Пл
S K i
: 6(i+1)/2
6 (i +1)/2
2 ( i -x ) + sin2 ^
cos—— 1 ( 1 -x ) + sin2—2
2 2 1 2
' 2 N 1 -12 N 1 -1 g
S S K i, sin ^f 2 i =13 i =1,3 2
+ SS k, cos 6 i =2 4 i =1 3 2
2 N 1 2 N 1 -1
' 2 N 1 -1 2 N 1
S S Kjsin i=1,3 j=2,4
2 N 1 2 N 1
X [ 2 (x+1) + cos2 H '
|_2 (Л ) 2
X 1 ( 1 -% ) - sin2 j + 2^ 2
X 1 ( x+ 1 ) + cos2 6
_ [ 2 (Л ) 2
X 2(1 -x) + sin 2-2^2
2 ( Л) 2
2 ( x+ 1 ) + cos2 ^
2 ( 1 -x ) + sin2 6 y
6 (i+1)/2
+ SS K i, cos ". i =2,4 j =2,4 2
- i , j + 2 N i -4
- 6(i+1)/2 sin
2 N 1
+ S K ii + 2N 1 -4
. j =2,4
6 i
+
+
;
;
■ 2 ( x+ 1 ) + cos2 " 2 ;
2 ( 1 -x ) + sin2 6 /2
2 ( x+ 1 ) + cos 2 °y
cos^ 2 ( 1 -x ) + sin2 ^
B = o (1 -П ) R 1/2
2 8 G V2 n
;
^ , j = 5,6...2 N 1 + 4;
15 [ ( 2 x - 2 ) sin 2 a - (5 x + 3) cos 2 a ] +
+1J
G
2 N 1 -12 N 1 -1 g
S S K ij sin + i =1 3 i =1 3 2
2 N 1 -1 2 N 1
+ S S K ij sin i =1,3 j =2,4
2 N 1 2 N 1 -1
2 ( x + 1 ) + cos2 6 2
6 ( i +1)/2 2
+ S S K j cos y-
i =2,4 j =1,3
2 N 1 2 N 1
+SS Ki i=2,4 j=2,4
6 i
2 ( x + 1 ) + cos1 ^y2
2 ( 1 -x ) + sin2 ^ X
cos 6 2 1 ( 1 -x ) + sin2 6 2 X
2 2V ' 2
5(cos( 6 (j + 1)/2 + 2 a ) + x cos( 6 ( j +1)/2 - 2 a ) -
- 2 sin 2 a sin 6 ( , + 1)/2 + ( x + 1) a cos 2 a
R (sin(2 a - 6 j /2) + x sin(2 a + 6 , /2) -- 2 cos 2 a sin 6 , V2 + ( x + 1) a sin 2 a
+
1 +
;
5 (cos( 6 ( j +1)/2 + 2 a ) + x cos( 6 ( j +1)/2 - 2 a )
- 2 sin 2 a sin 6(- + 1)/2 + ( x + 1) a cos 2 a
5 (sin(2 a - 6 ( , 41)/2 ) + x sin(2 a + 6 , -/2 ) -"
- 2 cos 2 a sin 6 j /2 + ( x + 1) a sin 2 a
+
2 N 1 -1 2 N 1 -1
K 33 = S S K j ; i =1,3 j =1,3
2 N 1 -1 2 N 1
k 34 = S S к, ;
i =1,3 j =2,4
2 N 1 -1
K 3j = S K ij+2N 1 -4 , j = 5,6...2 N + 4;
i =1,3
B 3 = 0;
2 N 1 2 N 1
к 44 = EE K ;
i =2,4 j =2,4
K 4 j = E K i,j + 2 N -4 , j = 5,6—2 N ■ + 4;
i =2,4
B 4 = 0;
B =o(1 -n)
i 8 G
2(2 N 1) 2 N 1
E EKjX i=2 Ni +1 j=1,3
R (cos( 6 ( j +i)/2 + 2 a ) + X cos( 6c-+i)/2 - 2 a ) -
- 2 sin 2 a sin 6 ( j + 1)/2 + ( x+ 1) a cos 2 a
2(2 N 1) 2 N 1
+ E E Kj x i=2 N1 +1 j =2,4
R (sin(2 a -6 j /2) + x sin(2 a + 6 j /2) -
- 2 cos 2 a sin 6 j /2 + ( x+ 1) a sin 2 a
^ - B,
’ i +2 N i -4 ,
K 12 = 0; K 14 = 0; B i = 0; K 22 = 0; K 23 = 0; K 24 = 0; K 2 j = 0, j = 5,6-2 N , + 4; B 2 = 0; K 34 = 0; B 3 = 0; K 44 = 0;
K 4j = 0, j = 5,6-2 N + 4; B 4 = 0; B i = 0, i = 5,6- Ng - 2 N , + 4;
K 13 =
' 2 N i -12 N i -1 g
E E K j cos 6 +12
i =i 3 j =i 3 2
2 ( x- i ) + sin2 ^
=
1 j G 22к
2 N i -1
E Ki
2 N i 2 N i-1 д
+ EE K j sin ^ i/ 2
i =2 4 i =i 3 2
• i , j +2 N i -4
6 (i+1)/2 cos
2 N 1
+ E K j2N i -4
2 ( X + 1 ) - cOs2 ^
2 ( X- i ) + sin2 ^
sin^^ 2(x+1)-cos2^^
6 i
;
, j = 5,6...2 N i + 4;
2 N i -1 2 N i -1
K 33 = EE K ij ;
i =1,3 j =1,3
K 3j = E1 K i,j + 2 N i - 4 , j = 5,6...2 N i + 4; i =1,3
K j = K + 2 N i -4, j +2 N i -4 , i , j = 5,6... N g - 2 N i + 4 .
Список литературы Формулировка метода конечных элементов с учетом сингулярности для плоской задачи смешанных форм разрушения
- Алямовский А.А. SolidWorks/Cosmos Works. Инженерный анализ методом конечных элементов. - М.: ДМК Пресс, 2004. - 432 с.
- Бабец Д.В., Сдвижкова Е.А., Сосна Д.О. Численное моделирование влияния поверхности трещин при оценке прочности породного массива // Вюник Криворiзького национального ушверситету. - 2018. - № 47. - С. 169-175.
- Бате К., Вильсон Е. Численные методы анализа и метод конечных элементов. - М.: Стройиздат, 1982. - 446 с.
- Вовк Л.П., Кисел Е.С. Моделирование распространения трещины из вершины острого V-образного выреза модели, ослабленной разгружающим отверстием // Журнал теоретической и прикладной механики. ДНУ. - 2019. - № 1 (66). -С. 18-30.
- Галанин М.П., Лазарева С.А. Метод конечных суперэлементов и его применение для решения задач науки и техники // Математическое моделирование. РАН. - 2013. - Т. 2, № 6. - С. 32-40.
- Галанин М.П., Ходжаева С.Р. Разработка и тестирование методов решения жестких обыкновенных дифференциальных уравнений // Математическое моделирование и численные методы. МГТУ им. Н.Э. Баумана. - 2014. - № 4. -С. 95-119.
- Галанин М.П., Лазарева С.А., Савенков Е.Б. Метод конечных суперэлементов для решения трехмерных задач теории упругости. Численное исследование // Препринты ИПМ им. М.В. Келдыша. Институт прикладной математики им. М.В. Келдыша РАН. - М., 2006. - № 44. - С. 1-29.
- Гумеров А.К. Новые задачи механики разрушения неоднородных тел // Сварка. Реновация. Триботехника: материалы IX Урал. науч.-практ. конф. Нижнетагильский технологический институт (филиал) УрФУ. - Нижний Тагил, 2019. -№ 9. - С. 127-133.
- Гумеров К.М., Харисов Р.А. Некоторые новые задачи механики разрушения // Тез. докл. Междунар. конф.: «Перспективные материалы с иерархической структурой для новых технологий и надежных конструкций» и «Химия нефти и газа» в рамках Международного симпозиума «Иерархические материалы: разработка и приложения для новых технологий и надежных конструкций». - Томск, 2018. - С. 103-104. DOI: 10.17223/9785946217408/58
- Гундина М.А. Энергетические инварианты в теории упругопластических трещин // СПб.: Наука и техника, 2017. - Т. 16, № 4. - С. 355-362. DOI: 10.21122/2227-1031-2017-16-4-355-362
- Метод граничных элементов для численного решения трехмерных задач механики трещин / А.В. Звягин [и др.] // Вестник кибернетики. - Сургут, 2020. - № 2. - С. 18-31.
- Кабо Е.А. Выделение сингулярности при численном решении задач механики трещин: автореф. дис. ... канд. физ.-мат. наук: 01.02.04. - СПб.: СПбГТУ, 1998. - 18 с.
- Кайтуков Т.Б., Мозгалева М.Л., Акимов П.А. Об использовании аппарата вейвлет-анализа в рамках метода конечных элементов для расчета строительных конструкций. Часть 2: Вейвлет-реализации метода конечных элементов на основе сплайн-вейвлетов // Фундаментальные, поисковые и прикладные исследования Российской академии архитектуры и строительных наук по научному обеспечению развития архитектуры, градостроительства и строительной отрасли Российской Федерации в 2018 году. - 2019. - С. 249-260.
- Каспарова Е.А., Шушпанников П.С. Численные и аналитические методы моделирования роста и взаимодействия трещин // Вычислительная механика сплошных сред. - 2018. - Т. 11, № 1. - С. 79-91.
- Лазарева С.А. Анализ точности приближений метода конечных суперэлементов Федоренко // Вестник МГТУ им. Н.Э. Баумана. Серия: Естественные науки. - 2009. -№ 2 (33). - С. 3-27.
- Лапин Р.Л. Расчет упругих и прочностных характеристик материалов с трещинами: автореф. дис. ... канд. физ.-мат. наук: 01.02.04. - СПб.: СПбПУ им. Петра Великого, 2019. - 224 с.
- Матвеенко В. П. Методы расчета и оптимизации напряженного состояния в окрестности особых точек упругих тел // Отчет о НИР/НИОКР. РФФИ: 96-01-00473-а. - 1998. -№ гранта 96-01-00473.
- Матвеенко В.П, Федоров А.Ю., Шардаков И.Н. Анализ сингулярности напряжений в особых точках упругих тел из функционально-градиентных материалов // Доклады Академии наук. РАН. - 2016. - Т. 466, № 1. - 38 с.
- Миронова Е.А., Степанова Л.В. Смешанное деформирование тел с разрезами в связанной постановке (ползучесть - поврежденность) // Сб. тр. III международной конференции и молодежной школы. Информационные технологии и нанотехнологии (ИТНТ 2017). СНИУ им. ак. С.П. Королева. -Самара: Изд-во ПНТ, 2017. - С. 1310-1313.
- Морозов Е.М., Никишков Г.П. Метод конечных элементов в механике разрушения. - М.: Изд-во ЛКИ, 2008. - 256 с.
- Назаров С. А. Базисы сингулярных решений в задачах механики трещин // Вестник СПбУ. Математика. Механика. Астрономия. - 2008. - № 4. - С. 21-34.
- Нифагин В.А., Гундина М.А. Напряженно-деформированное состояние в окрестности вершины трещины для неголономной пластичности в условиях плоского напряженного состояния // Механика машин, механизмов и материалов. Объединенный институт машиностроения НАН Белоруси. -Минск, 2012. - № 1(18). - С. 47-52.
- Эффекты пластической дисторсии в зоне кривизны кристаллической решетки в вершине трещины / В. Е. Панин, М.Д. Моисеенко, П.В. Максимов, С.В. Панин // Физическая мезомеханика / Ин-т физики прочности и материаловедения Сибирского отделения РАН. - Томск, 2017. - Т. 20, № 3. -С. 40-50.
- Парис П., Си Дж. Анализ напряженного состояния около трещин // В кн.: Прикладные вопросы вязкости разрушения. - М., 1968. - С. 64-130.
- Перельмутер М.Н. Моделирование кинетики самозалечивания трещин // Физическая мезомеханика. - 2019. -Т. 22, № 4. - С. 47-55.
- Побережный Д.И. Сингулярность напряжений при численном моделировании методом конечных элементов // М.: Аллея науки, 2017. - Т. 2, № 15. - С. 634-646.
- Прищепа Д.В., Латышев О.Г. Использование метода конечных элементов для исследования напряженно-деформированного состояния трещиноватого породного массива // Инновационные геотехнологии при разработке рудных и нерудных месторождений. - Екатеринбург, 2017. -Т. 18, № 1. - С. 257-264.
- Рукавишникова Е.И. Сходимость метода конечных элементов для краевой задачи с вырождением на всей границе области // Вестник Южно-Уральского государственного университета. Серия: Вычислительная математика и информатика. - 2019. - Т. 8, № 3. - С. 5-26.
- Степанова Л.В. Математические методы механики разрушения. - М.: Физматлит, 2009. - 334 с.
- Степанова Л. В. Асимптотика напряжений и скоростей деформаций вблизи вершины трещины поперечного сдвига в материале, поведение которого описывается дробно-линейным законом // Прикладная механика и техническая физика. Сибирское отделение РАН. - Новосибирск, 2009. -Т. 50, № 1 (293). - С. 165-176.
- Степанова Л.В., Адылина Е.А. Асимптотические методы нелинейной механики разрушения: результаты, современное состояние и перспективы // Вестник СГТУ. Серия: Физико-математические науки. - Самара, 2012. - № 2 (31). -С. 156-168.
- Степанова Л.В., Белова О.Н., Туркова В.А. Определение коэффициентов разложения М. Уильямса поля напряжений у вершины трещины с помощью метода цифровой фотоупругости и метода конечных элементов // Вестник Самарского университета. Естественнонаучная серия. - 2019. -Т. 25, № 3. - С. 62-82.
- Степанова Л.В., Игонин С.А. Параметр поврежден-ности Ю.Н. Работнова и описание длительного разрушения: Результаты, современное состояние, приложение к механике трещин и перспективы // Прикладная механика и техническая физика. Сибирское отделение РАН - Новосибирск, 2015. -Т. 56, № 2 (330). - С. 133-145.
- Хечумов Р.А., Кепплер Х., Прокофьев В.И. Применение метода конечных элементов к расчету конструкций. -М.: Изд-во Ассоциации строительных вузов, 1999. - 352 с.
- Черепанов Г.П. Механика хрупкого разрушения. -М.: Наука, 1974. - 640 с.
- Шлянников В.Н. Определение критериев механики разрушения при многоосном внешнем нагружении. // В кн.: Технология производства и прочность деталей летательных аппаратов и двигателей. - Казань, 1979. - С. 73-82.
- Шлянников В.Н., Тартыгашева А.М. Влияние пластических свойств стали на состояние вершины трещины // Известия вузов. Проблемы энергетики / КГЭУ. - Казань, 2004. - № 11-12. - С. 56-67.
- Шлянников В.Н., Туманов А.В. Силовая и деформационная модели поврежденности и разрушения при ползучести // Физическая мезомеханика / Ин-т физики прочности и материаловедения Сибирского отделения РАН. - Томск, 2018. - Т. 21, № 3 - С. 70-85.
- Щербаков С.С. Математическое моделирование и вычислительная механика: потенциал для роста наукоемкой экономики // Наука и инновации. - 2019. - № 1. - С. 45-53.
- Simulation of thermoplastic crack problems using singular edge-based smoothed finite element method / H. Chen, Q. Wang, G.R. Liu, Y.Wang, J. Sun // International Journal of Mechanical Sciences. - 2016. - No. 115. - Р. 123-134.
- Eftis J., Subramoian N. The inclined crack under biaxial load // Engineering fracture mechanics. - 1978. - Vol. 10, no. 8. -P. 48-67.
- Eftis J., Subramoian N., Libowitz H. Crack border stress and displacement equations revisited // Engineering fracture mechanics. - 1977. - Vol. 9, no. 1. - P. 189-210.
- Eftis J., Subramoian N., Libowitz H. Biaxial and effects on the crack border elastic strain energy density and strain energy rate // Engineering fracture mechanics. - 1977. - Vol. 9, no. 4. -P. 753-764.
- A gradient weighted extended finite element method (GW-XFEM) for fracture mechanics / S.Z. Feng, S.P.A. Bordas, X. Han, G. Wang, Z.X. Li // Acta Mechanic. - 2019. - No. 230(7). -P. 2385-2398.
- Galanin M.P., Savenkov E.B. Combined use of the finite element and finite superelement methods // Computational Mathematics and Mathematical Physics. - 2006. - Vol. 46, no. 2. -P. 258-270.
- Hell S., Becker W. An Enriched Scaled Boundary Finite Element Method for 3D Cracks // Engineering Fracture Mechanics. - 2019. - No. 215. - P. 272-293.
- Hilton P.D. Plastic intensity factors for cracked plates subjected to biaxial loading // International journal of fracture. -1973. - Vol. 9, no. 2 - P. 176-156.
- Hilton P.D., Sih G.C. Applications of the finite element method to the calculations of stress intensity factors // Mechanics of fracture methods of analysis and solution of crack problem. -1973. - Vol. 1 - P. 426-483.
- Hutchinson J.W. Plastic stress and strain fields at a crack tip // Journ. Mech. Phys. Solids. - 1968. - Vol. 16 - P. 337-347.
- Hutchinson J.W. Singular behavior at the end of a tensile crack in a hardening material // Journ. Mech. Phys. Solids. -1968. - Vol. 16. - P. 13-31.
- Li H., Li J., Yuan H. A review of the extended finite element method on macrocrack and microcrack growth simulations // Theoretical and Applied Fracture Mechanics. - 2018. - No. 97. -P. 236-249.
- Efficient integration of crack singularities in the extended finite element method: Duffy-distance transformation and con-formal preconditioning strategy / J.H. Ly, Y.Y.Jiao, P. Wriggers, T. Rabczuk, X.T. Feng, F. Tan // Computer Methods in Applied Mechanics and Engineering. - 2018. - No. 340. - P. 559-576.
- Michavilla F., Gavete L. Some results in two and three dimensional singular finite elements with applications to fracture mechanics // Proc. 4th Int. Symp., Atlanta GA. - 1986. - P. 417-422.
- Investigating of chemical effects on rock fracturing using extended finite element method / E. Mohtarami, A. Baghbanan, M. Eftekhari, H. Hashemolhosseini // Theoretical and Applied Fracture Mechanics. - 2017. - No. 89. - P. 110-126.
- Murakami J. A simple procure for the accurate determination of stress intensity factors by finite element method // Engineering fracture mechanics. - 1976. - Vol. 8, no. 4. - P. 643-655.
- Murakami S. Continuum Damage Mechanics: A Continuum Mechanics Approach to the Analysis of Damage and Fracture. - Dordrecht: Springer, 2012. - 423 p.
- Nojumi M.M., Wang X. Dynamic analysis of crack problems in functionally graded materials using a new graded singular finite element // Theoretical and Applied Fracture Mechanics. - 2018. - No. 93. - P. 183-194.
- Rice J.R. A path Independent integral and the approximate analysis of strain concentration by notches and cracks // Journal of Applied Mechanics. - 1968. - Vol. 35. - P. 379-386. doi.org/10.1115/1.3601206
- Rice J.R., Rosengren G.F. Plane strain deformation near a crack tip in a power-law hardening material // Journ. Mech. Phys. Solids. - 1968. - Vol. 16. - P. 1-12.
- Richard H.A., Schramm B., Schrimeisen N.H. Cracks on Mixed Mode loading - Theories, experiments, simulations // International Journal of Fatigue. - 2014. - No. 62. - P. 93-103.
- Song C., Ooi E.T., Natarajan S. A review of the scaled boundary finite element method for two-dimensional linear elastic fracture mechanics // Engineering Fracture Mechanics. - 2018. -No. 187. - P. 45-73.
- Shlyannikov V.N. Modelling of crack growth by fracture damage zone // Theoretical and Applied Fracture Mechanics. - 1996. -Vol. 25. - P. 187-201. doi.org/10.1016/S0167-8442(96)00021-3
- Generalization of mixed mode crack behavior on the base of nonlinear fracture resistance parameters / V.N. Shlyannikov, A.P. Zakharov, A.V. Tumanov, A.M. Tartygasheva // Procedia Structural Integrity. - 2018. - Vol. 13 - P. 1117-1122. doi.org/10.1016/j.prostr.2018.12.234.
- Shlyannikov V.N., Tumanov A.V. Characterization of crack tip stress fields in test specimens using mode mixity parameters // International Journal of Fracture. - 2014. - Vol. 185, iss. 1. -P. 49-76. doi.org/10.1007/s10704-013-9898-0
- Shih C.F. Small scale yielding analysis of mixed mode plane-strain crack problems // Fracture Analysis ASTM STP 560. -1974. - P. 187-210.
- Stepanova L.V. Asymptotic self-similar solution of the creep crack problems in damaged materials under mixed mode loading // Applied Mechanics and Materials. - 2015. - Vol. 784. -P. 145-152.
- Stepanova L.V. Stress-strain state near the crack tip under mixed-mode loading: Asymptotic approach and numerical solutions of nonlinear eigenvalue problems // AIP Conference Proceedings. - 2016. - Vol. 1785(030030) - P. 1300. DOI: 10.1063/1.4967051
- Stepanova L.V., Yakovleva E.M. Asymptotic stress field in the vicinity of the mixed-mode crack in damaged materials under creep conditions // Procedia Structural Integrity. - 2016. -Vol. 2. - P. 793-800.
- Elasto-plastic stresses and strain in a cracked plate / J. Swedlow [et al.] // Proceeding international journal of fracture. -1976. - Vol. 12, no. 3. - P. 359-368.
- Torabi A.R., Abedinasab S.M. Brittle fracture in keyhole notches under mixed mode loading: Experimental study and theoretical predictions // Engineering Fracture Mechanics. - 2015. -No. 134. - P. 35-53.
- Tumanov A.V., Shlyannikov V.N., Chandra Kishen. An algorithm of automatization and experimental study of mixed mode crack growth rate based on drop potential method // International Journal of Fatigue. - 2015. - Vol. 81 - P. 227-237. doi.org/10.1016/j.ijfatigue.2015.08.005.
- Zienkiewicz O.C., Taylor R.L. The finite element method. V. 1. The Basic. - London: Butterworth Heinemann, 2000. - 712 p.
- Zienkiewicz O.C., Taylor R.L. The finite element method. V. 2. Solid Mechanics. - London: Butterworth Heinemann, 2000. - 480 p.
- WeiBgraeber P., Leguillon D., Becker W. A review of Finite Fracture Mechanics: crack initiation at singular and nonsingular stress raisers // Archive of Applied Mechanics. - 2016. -No. 86 (1-2). - P. 375-401.
- Wriggers P. Nonlinear finite element method. - Berlin: Springer, 2008. - 560 p. DOI: 10.1007/978-3-540-71001-1.
- Xin H., Veljkovic M. Fatigue crack initiation prediction using phantom nodes-based extended finite element method for S355 and S690 steel grades // Engineering Fracture Mechanics. -2019. - No. 214. - P. 164-176.
- Zhang R., Guo R. Determination of crack tip stress intensity factors by singular Voronoi cell finite element model // Engineering Fracture Mechanics. - 2018. - No. 197. - P. 206-216.


