Формулы для прогибов и упрощенный метод Данкерли для расчета частоты колебаний плоской фермы

• 1    Введение / Introduction

Расчет стержневых строительных конструкций, как правило, выполняется в различных специализированных инженерных пакетах, в основе которых лежат численные методы [1], [2]. Возможной альтернативой численным решениям являются аналитические методы, полученные как индукцией в системах компьютерной математики [3], [4], так и разложением в ряды [5,6]. Наиболее эффективны решения для регулярных конструкций, в которых находится зависимость прогибов, прочности или частот собственных колебаний от порядка регулярности (числа периодических структур). Число регулярных статически определимых ферм ограничено. Проблему существования регулярных статически определимых ферм впервые подняли Hutchinson R. G. и Fleck N. A. [7], [8], назвавшие поиск таких схем "охотой". Этим же вопросом в задачах оптимизации конструкций занимался A. Kaveh [9], [10]. Простая математическая модель для анализа свободных колебаний комбинированных ферм на основе метода Донкерлея разработана в [11].

В справочнике автора [12] приведено более 70 схем балочных ферм, арок и рам, допускающих аналитические решения для величины прогиба (или смещения опоры) в системе Maple. Расчет статического прогиба плоской балочной фермы с двойной решеткой в зависимости от числа панелей приведен в аналитической форме в работе [13]. В [14] получены формулы для прогиба фермы рамного типа с треугольной решеткой в ригеле. Формулы для первой собственной частоты плоских ферм выведены методом индукции в [4], [15], [16]. Методом Донкерлея в [17] в системе Maple выведена формула для первой частоты колебаний шпренгельной фермы. Метод Донкерлея используется в [18] для оценки собственной частоты колебаний сложных комбинированных сооружений на ранних стадиях проектирования конструкций до ее полного динамического анализа. Аналитический расчет прогиба внешне Kirsanov, M.

Formulas for deflections and a simplified Dunkerley method for calculating the vibration frequency of a planar truss

статически неопределимой фермы выполнен в [19]. Известны некоторые решения для пространственных статически определимых ферм [3], [20]. В [21] выполнен аналитический расчет прогиба пространственной модели составной рамы с произвольным числом панелей. Первая собственная частота плоской фермы Финка рассчитана аналитически в [22]. Решение задачи о пространственной ферме в нелинейной постановке получено Галишниковой В.В. [23].

В настоящей работе предлагается новая схема плоской статически определимой фермы рамного типа и упрощенный вывод формул зависимостей прогиба и первой частоты ее собственных колебаний от числа панелей. Прогиб находится по формуле Максвелла – Мора. Нижняя оценка первой частоты в аналитической форме получается методом Донкерлея и предложенным упрощенным методом, дающим одновременно более точное и компактное решение. Это решение может служить тестовым для оценки первой частоты, полученной в более сложной постановке численным методом.

• 2    Материалы и методы / Materials and Methods

2.1 Схема фермы, составление уравнений

Ферма имеет 2 n панелей в пролете и состоит из п = 8 n + 6 стержней, включая три стержня, моделирующие левую подвижную и правую неподвижные опоры (рис. 1).

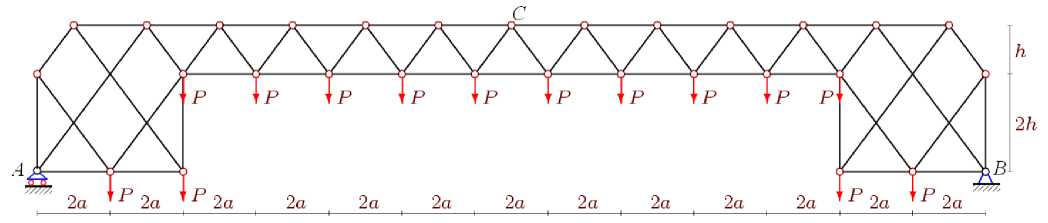
Рис. 1. – Схема фермы, n=7

Fig. 1. – Truss scheme, n=7

Ферма статически определимая. Усилия в стержнях определяются методом вырезания узлов одновременно с тремя реакциями опор. Все аналитические преобразования выполняются в системе Maple. Для этого вводится система отсчета, и вычисляются координаты узлов. Начало координат помещается в левую подвижную опору A (рис. 2):

L0 = 2a(2n -1), x1 = 0, x2 = 2a, x3 = 4a, y = y2 = y3 = 0, xi+3 = 2(i +1)a, yi+3 = 2h, i = 1,...,2(n - 2), x2 n = L0 - 4 a, x2 n+1 = L0 - 2 a, x2 n+2 = Lo, y 2 n = y 2 n+1 = y 2 n+2 = 0, x 2 n+3 = 0, y 2 n+3 = 2 h, xi+2n +3 = (2i - 1)a, У1+2n+3 = 3h, i = U",2n - 1, x4 n+3 = L0, y 4 n+3 = 2 h.

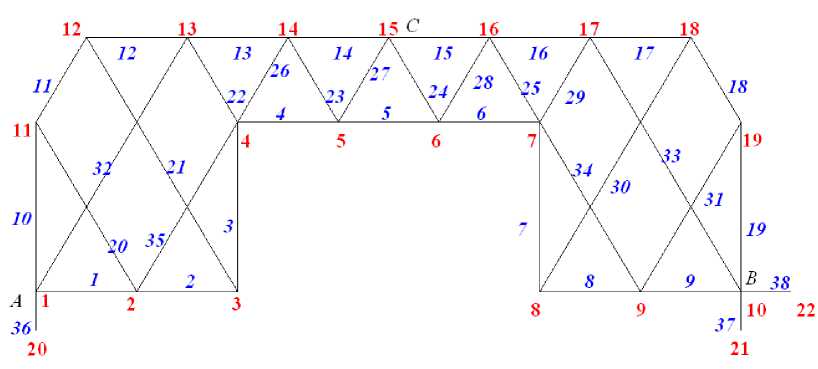
Рис. 2. – Нумерация стержней и узлов фермы, n =4

Fig. 2. – Numbering of truss nodes and members, n=4

Структура решетки определяется порядком соединения стержней в узлы и вводится в текст программы с помощью специальных списков номеров концов соответствующих стержней. Стержни нижнего пояса, например, кодируются следующими номерами их концов:

Ф i = [ i , i + 1], i = 1,..,2 п + 1.

Эти списки неориентированы. На величину и знак усилия выбор начала и конца стержня не влияет. Точно также кодируются и остальные стержни, включая три опорные.

2.2 Расчет усилий в стержнях

Усилия в статически определимой конструкции вычисляются из решения системы уравнений равновесия узлов GS=B , где G — матрица направляющих косинусов усилий, составленная по координатам узлов и спискам номеров узлов по концам стержней Ф i , i = 1,.., n , S — объединенный вектор неизвестных усилий и реакций опор, B — вектор нагрузок на узлы. Каждому узлу фермы соответствует по две строки матрицы G и два элемента вектора нагрузок с теми же номерами. В нечетные элементы вектора нагрузок B ₂ i _{- 1} вносятся проекции внешних сил, приложенных к узлу i в проекции на ось x , в четные — проекции сил на ось y . Направляющие косинусы векторов усилий на оси координат вычисляются по данным о координатах узлов и структуре решетки:

l = X — x^ ) / l , l = X* — У*. ) / l , i = 1,..., У,

• x, i       V Ф-, Ф₉' ' i, y, i           Ф Фо' ' i,             ,     , ,

2.3    Прогиб

^,                         i ,1                   i ,2                       y ,                        i ,1                   i ,2

где l i = ^ l ^ i + l^ — длина стержня i . Матрица коэффициентов уравнений равновесия заполняется по строкам. Каждые две строки соответствуют одному узлу и уравнениям проекций на оси x и y :

G = l / l ,, G    . = l / l .,

2Ф i 1 —1, i         x , i ¹ i' 2Ф i 1 , i         y , i ¹ i'

G^ ■ = ¹ / 1 , G^ -=-¹ / 1 • 2Ф i 2 —1, i             x , i ¹ i' 2Ф i 2 , i            У , i ¹ i

Здесь учтено, что направляющие косинусы усилий, приложенных к разным концам одного стержня, имеют разные знаки.

Для случая равномерно распределенной нагрузки по узлам нижнего пояса последовательность решений задачи о прогибе имеет вид:

n = 3: A = P(192a3 +102c3 + 22h3) / (h2EF), n = 4: A = P(656a3 +148c3 + 32h3)/(h2EF), n = 5 : A = P(1648a3 +196c3 + 42h3) / (h2EF), n = 6: A = P(3488a3 + 246c3 + 52h3)/(h2EF),...

где c = 7 a ² + h² . Обобщение коэффициентов в последовательности полученных выражений с использованием операторов Maple дает следующую формулу для расчета прогиба:

A = P ( C 1 a ³ + C ₂ c ³ + C ₃ h ³)/( h ² EF ),                                    (1)

где

C 1 = 2(5 n ⁴ - 10 n ³ + 31 n ² - 26 n - 48)/3,

C ₂ = n ² + 39 n - 24, C ₃ = 10 n - 8.

Аналогично, для случая нагружения узлов верхнего пояса (рис. 3) коэффициенты будут иметь вид:

C 1 = (20 n ⁴ - 40 n ³ + 34 n ² - 14 n + 3) / 6,

C 2 = (2 n ² + 78 n - 95)/2,

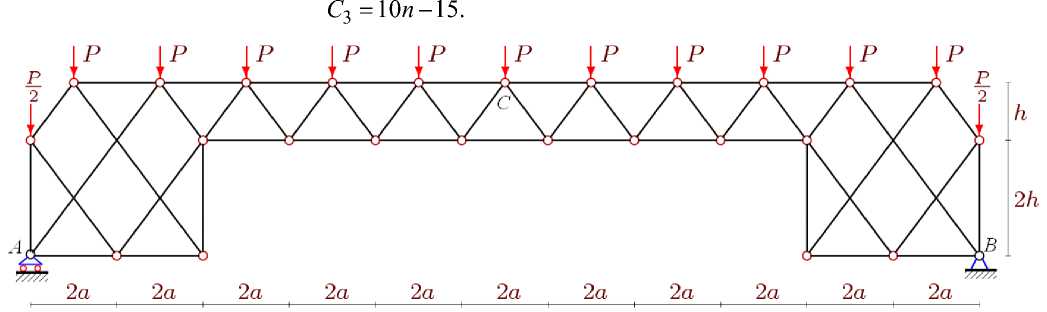
Рис. 3. – Нагрузка на верхний пояс фермы, n=6

Fig. 3. – Load on the upper belt of the truss scheme, n=6

Наиболее простые коэффициенты в (1) получаются для решения задачи о прогибе середины пролета фермы под действием одной сосредоточенной силы в узле C :

C 1 = (2 n - 1)(8 n ² - 8 n + 3)/6, C ₂ = (2 n + 39)/2, C ₃ = 5.

2.4    Смещение опоры

Рассматриваемая ферма безраспорная. Действие вертикальной нагрузки вызывает горизонтальное смещение левой подвижной опоры. Для балочных ферм эта величина незначительная. В фермах арочного и рамного типа смещение опоры может быть большим и должно учитываться при проектировке сооружения. В случае нагрузки, распределенной по узлам верхнего пояса (рис. 3), эта величина имеет вид:

8 = P ( C 1 a ³ + C 2 c ³ + C 3 h ³) / ( haEF ).                                      (2)

От формулы (1) для прогиба эта зависимость по форме отличается лишь знаменателем. Коэффициенты в ней также находятся методом индукции:

C 1 = (2 n - 1)(20 n ² - 20 n - 3) /3, C 2 = 64 n - 78, C ₃ = 20 n - 30.                 (3)

При действии распределенной нагрузки по узлам нижнего пояса (рис. 1) вид зависимости (2) прогиба от числа панелей не меняется, а коэффициенты имеют вид:

C 1 = 4(10 n ³ - 15 n ² + 59 n - 114)/3, C 2 = 64 n - 44, C 3 = 4(5 n - 4).

Формула (2) справедлива и для случая действия сосредоточенной вертикальной силы в среднем узле пролета C. Соответствующие коэффициенты имеют вид:

C 1 = 10 n ² - 10 n - 1, C ₂ = 32, C 3 = 10.

2.5    Первая собственная частота колебаний

Рассматривается распространенная модель инерциальных свойств фермы: масса фермы концентрируется в ее узлах равномерно по всей конструкции. Каждая масса имеет одну степень свободы – движение по оси y . Система масс в рассматриваемой ферме имеет число степеней свободы K = 4 n + 3 . Систему дифференциальных уравнений колебаний масс в узлах можно записать в матричном виде:

M к Y + D K Y = 0                            (4)

где Y – объединенный вектор всех перемещений узловых масс длиной K , D _K – матрица жесткости системы, M K - матрица инерции, Y — вектор ускорений. В случае одинаковых масс матрица инерции пропорциональна единичной матрице M K = m I K . Матрица податливости B K , обратная к матрице жесткости D _K , находится по формуле Максвелла – Мора:

b . = у s ⁽ i ) s ⁽ j ) l /(EF ),                                      (5)

, j             a a a a=1

где S a i ) — усилие в стержне a от действия единичной силы в узле i, приложенной по направлению перемещения . Если умножить слева уравнение (4) на матрицу податливости B _K , то задачу можно свести к проблеме собственных чисел матрицы B K : B K Y = X Y , где X = 1 / ( m ш ²) — собственное число матрицы B K , ш — собственная частота колебаний. Отсюда частота колебаний выражается через собственные числа матрицы податливости и имеет вид:

ш = J 1 / (m X ) .

Аналитически получить значения собственных частот колебаний можно лишь для фермы с одной панелью, и то если число узлов не больше четырех. Однако есть несколько методов нахождения границ первой частоты. Нижнюю границу этой частоты дает формула Донкерлея:

K шХ = Е шХ                          (6)

i = 1

где ш_г — парциальная частота колебания массы m , расположенной в узле i [24]. Для вычисления парциальных частот ш_г достаточно использовать скалярную форму уравнения (4):

mu. + du. = 0, i ii где ui - смещение массы по оси y, Ui- вектор ускорения, di - коэффициент жесткости (i — номер узла фермы с массой m). Частота колебаний груза в узле i: ш. = dd. / m . Величина жесткости вычисляется через коэффициент податливости, определяемый по формуле Максвелла – Мора:

~^\2

« . = 1/ d i = E ( S 1 i ¹ ) l a KEF ) a =1

Здесь обозначено S ^ . ) — усилия в стержне с номером а от действия единичной силы, приложенной к узлу i . Из (6) и (7) следует:

K         K        K ^

F = m Е 7 = m Е * = m EE S ! ¹) l_a / (EF ) = m E. i =1 d          i =1             i =1 a =1

Последовательный расчет E в аналитической форме в системе Maple при различных n дает следующие значения:

n = 3: Е = (14345a3 + 8905c3 + 3307h3) / (50EFh2), n = 4: e = (97601a3 + 29105c3 + 9277h3) / (98EFh2), n = 5: Е = (414753a3 + 68801c3 + 20095h3)/(162EFh2). n = 6: E = (1336489a3 +135161 c3 + 37169h3)/(242EFh2),...

Общий вид этих сумм: E = ( C 1 a ³ + C 2 c ³ + C ₃ h ³) / ((2 n - 1)² h ² EF ), где коэффициенты определяются методами системы Maple из решения рекуррентных уравнений:

C 1 = (2 n - 1)(1024 n ⁵ - 2560 n ⁴ + 2720 n ³ + 13840 n ² - 50934 n + 42435) / 90,

C 2 = (64 n ⁴ + 2432 n ³ - 6148 n ² + 2452 n + 3843) / 6,                                     (8)

C 3 = (704 n ³ -1176 n ² + 94 n + 1215) / 6.

В результате нижняя оценка для первой собственной частоты свободных колебаний фермы по методу Донкерлея принимает вид:

ш

D

= h

EF m (C1a3 + C2c3 + C3 h3)

3 Результаты и обсуждения / Results and Discussion

3.1    Смещение опоры. Пример

Решение (2), полученное для сдвига опоры A в трех случаях нагружения можно проиллюстрировать соответствующими графиками. Принята высота h =2м, пролет фермы L ₀ = AB = 100 м . Длина a зависит от числа панелей: a = L ₀/(4 n - 2) . Вводится безразмерная величина сдвига t = t EF /( P_sumL ₀), где в случае равномерно распределенной нагрузки P_sum = 2 nP , а в случае сосредоточенной нагрузки P_sum = P .

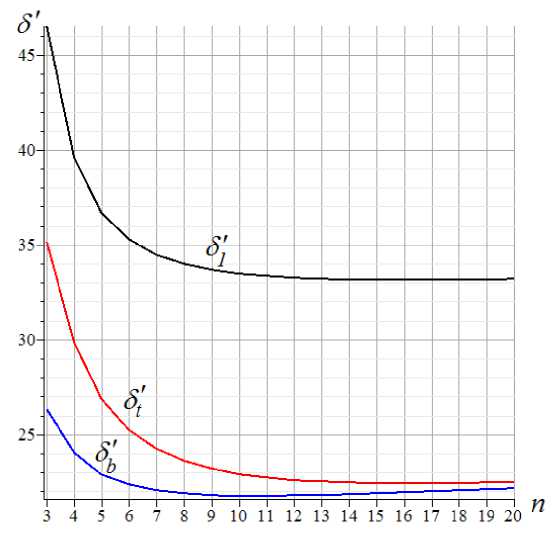
Рис. 4. - Сдвиг опоры A . 51' — сосредоточенная нагрузка; 5 t ' — нагрузка на верхний пояс;

5 b ' — нагрузка на нижний пояс фермы;

Fig. 4. - Shift of the support A . 51' — concentrated load; 5t' — load on the upper belt; 5b' — load on the lower belt of the truss

Ход кривых подсказывает наличие асимптот. Действительно, на основании (2) с коэффициентами (3), вычисленными для нагрузки по верхнему поясу, имеем предел:

lim 5 t ’/ n = 21 h ² /1250.

n →∞

Для сдвига опоры под действием двух других нагрузок (сосредоточенной и по нижнему поясу) результат оказывается таким же. Фактически этот предел равен тангенсу угла наклона асимптоты, а так как это значение положительное, то отсюда следует, что при больших значениях числа панелей сдвиг возрастает, хотя сначала он убывал. Следовательно, для всех трех случаях нагружения относительный сдвиг при каких-то числах n принимает минимальное значение. Судя по рисунку 4, зависимость 5 _b '( n ) минимальна при n =10.

3.2    Оценка первой частоты собственных колебаний. Пример

Приближенное аналитическое решение (9) имеет сравнительно сложный вид коэффициентов (8). Связано это прежде всего с необходимостью суммировать квадраты обратных значений парциальных частот

K

Е Ь i=1

и последующим обобщением полученных сумм.

Однако есть способ упростить эти действия [25]. Суммирование с большой точностью можно заменить площадью треугольника с основанием K, образованного ординатами 5:

K

Е 0 = Е 5 = 5 max K /2. Обобщение этих произведений, вычисленных для разных n на

• = 1

произвольный случай, во-первых, не составляет труда, во-вторых, дает более компактный результат. Соответствующая последовательность имеет вид:

n = 3: S ₀ = 15(85 a ³ + 45 c ³ + 11 h ³)/(4 EFh ² ), n = 4: E ₀ = 19(231 a ³ + 47 c ³ + 11 h ³) / (4 EFh ² ), n = 5: S ₀ = 23(489 a ³ + 49 c ³ + 11 h ³)/(4 EFh ² ), n = 6: S ₀ = 27(891 a ³ + 51 c ³ + 11 h³)/(4EFh ²),...

Общий вид элементов последовательности для произвольного n: Z0 = (C1 a3 + C2 c3 + C3 h3) / (EFh2), где коэффициенты определяются методом индукции:

C 1 = (4 n + 3)(2 n - 1)(8 n ² - 8 n + 3) /12,

C 2 = (4 n + 3)(2 n + 39)/4,                                       (10)

C ₃ = 11(4 n + 3)/4.

Таким образом, приближенное значение первой частоты по упрощенному методу Донкерлея имеет вид:

ш* = 2 h *

EF

m (4 n + 3)((2 n — 1)(8 n²

— 8 n + 3) a ³ /3 + (2 n + 39) c ³ + 11 h ³) ’

Приближенное решение (11) с константами (10) заметно проще, чем решение (9). Полиномы в константах решения (11) не выше четвертого порядка, полиномы в (8) имеют шестой порядок.

Для оценки погрешности приближенных решений для первой частоты a _D (9) и ® „ (10) можно численно найти первую частоту всего спектра частот из матричного уравнения (4) с помощью оператора Eigenvalues системы Maple.

Матрица B формируется в цикле. Соответствующий фрагмент программы на языке Maple имеет вид:

• >    for i to K do

• >    for j to K do

• >   B[i,j]:=add(S[i][k]*S[j][k]*L[k],k=1 ..ns);

• >    end:end:

Здесь п = ns — число стержней, S[i][k] — усилие в стержне k от единичной вертикальной нагрузки, приложенной к узлу i . Собственные числа Л вычисляются оператором Lm:=Eigenvalues(B/EF).

Три решения задачи о зависимости первой частоты от числа панелей представлены кривыми на рисунке 5. Принята масса грузов в узлах m =400 кг, модуль упругости всех стержней фермы E = 2,1 • 10⁵ МПа, площадь поперечных сечений F = 36 см ² , высота h =4м. С увеличением числа панелей первая частота по всем трем решениям монотонно уменьшается. При любом n решение Донкерлея ш D дает наименьшее значение. Приближенное решение ш * либо немного выше, либо ниже численного, условно принятого за эталон, так как при его нахождении решалась задача о колебании системы со всеми степенями свободы и никаких упрощений не делалось. Более точно оценить степень приближения двух рассмотренных приближенных аналитических решений можно по значению относительных погрешностей £ D = \ u D — ш 1 |/ ш 1 и г * = | ш * — ш 1 |/ ш 1 . На рисунке 6 показано изменение этих величин в зависимости от числа панелей для разных высот фермы.

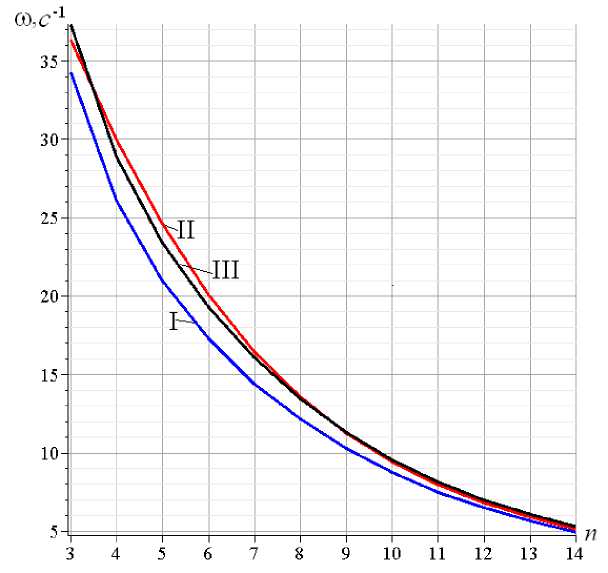
Рис. 5. – Первая частота колебаний, полученная тремя способами в зависимости от числа панелей n . I — метод Донкерлея ^ D ; II— упрощенный метод ш * ; III — численный метод ш 1 Fig. 5. – The first oscillation frequency obtained by three methods depending on the number of panels n . I — the Dunkerley method ш D ; II—simplified method ш * ; III — the numerical method ш 1

Наибольшую погрешность метод Донкерлея имеет при n =5 или n =6 в зависимости от высоты фермы. В любом случае погрешность этого решения уменьшается с увеличением числа панелей. Погрешность же предлагаемого приближенного метода ведет себя хаотично. Точность этого метода может быть и больше, и меньше в зависимости от высоты и числа панелей.

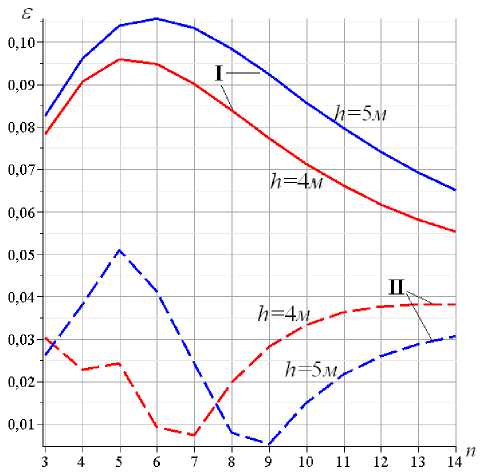
Рис. 6. – Относительная погрешность решений. I — метод Донкерлея; II – упрощенный метод, Fig. 6. – Relative error of decisions. I — the Dunkerley method; II — simplified method

Но главное – практические вычисления на предлагаемом примере показывают, что величина ш * одновременно и проще, и в несколько раз точнее, чем исходный метод Донкерлея. У предлагаемого метода есть один недостаток. Если метод Донкерлея дает гарантировано нижнюю оценку, то утверждать подобное про упрощенный метод нельзя. На рисунке 5 кривые Kirsanov, M.

Formulas for deflections and a simplified Dunkerley method for calculating the vibration frequency of a planar truss

а * и щ меняются местами при разном числе панелей, это означает, что при одних числах панелей упрощенное решение — это оценка сверху, при других — это оценка снизу.

Следует отметить, что в известных решениях для первой частоты собственных колебаний ферм методом Донкерлея точность оценок получается хуже. В среднем погрешность метода парциальных частот бывает около 30%. В рассматриваемой задаче точность решений значительно выше, а упрощенный метод одновременно более точный (погрешность около 3%) и более компактный (10).

• 4    Заключение / Conclusions

Основные результаты работы:

• 1.    Рассмотрена новая схема плоской статически определимой регулярной фермы.

• 2.    Методом индукции выведены формулы для прогиба фермы и сдвига подвижной опоры для трех типов нагрузки. Найдены асимптотики решения.

• 3.    Получена компактная формула для приближенного значения первой частоты. Результат сопоставлен с известным методом Донкерлея и численным методом. Показано, что точность аналитической оценки увеличивается с числом панелей.

• 5    Fundings / Финансирование

  Работа выполнена при финансовой поддержке РНФ 22-21-00473.