Фрагильность и параметр уравнения стеклования

Настоящее сообщение посвящено установлению взаимосвязи параметра уравнения стеклования δT g с фрагильностью m и проверке наличия линейной корреляции между величиной δT g и температурой стеклования T g .

В последние десятилетия получило распространение понятие о фрагиль-ности стекол m , которая определяется температурной зависимостью вязкости η ( T ) вблизи температуры стеклования T g [1-4]

m =

d ln n ( T ) d ( TJT )

T = T g

Легко убедиться, что подстановка зависимости η ( T ) из известного уравнения ВЛФ [5] в это выражение приводит к соотношению [2]

C m = — T C2 g

, где С1 и С2 — параметры уравнения ВЛФ. Через эти параметры выражается параметр уравнения δTg = С2/С1, характеризующий область перехода от жидкости к стеклу в процессе охлаждения стеклообразующих расплавов [6]. Из равенства (2) с учетом δTg=C2/C1 при m = const у стекол одного класса вытекает линейная корреляция между δTg и температурой стеклования Tg

I Tg

, что подтверждается экспериментальными данными (рис. 1-3).

Величина m используется для классификации стекол [1].

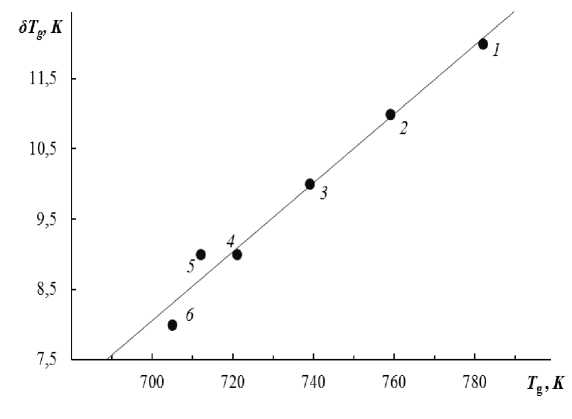
Рис. 1. Линейная корреляция между δT g и T g для натриево-силикатных стекол. Содержание Na 2 O, мол. %: 1 — 15, 2 — 20, 3 — 25, 4 — 30, 5 — 33, 6 — 35. Использованы данные [7].

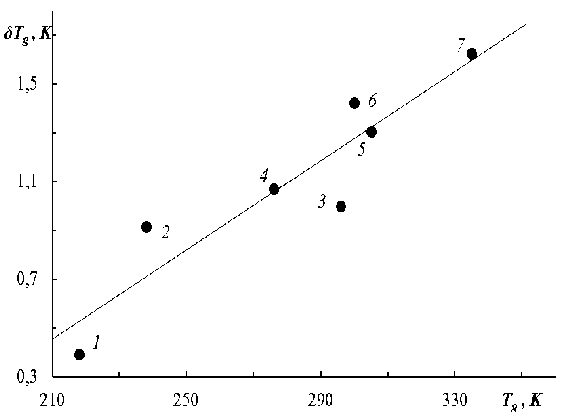
Рис. 2. Линейная корреляция между δT g и температурой стеклования T g для аморфных органических полимеров. 1 — полигексен-1, 2 — полиуретан, 3 — поливинилхлорацетат, 4 — полиметилакрилат, 5 — поливинилацетат, 6 — натуральный каучук, 7 — метакрилат этиловый. Использованы данные [5].

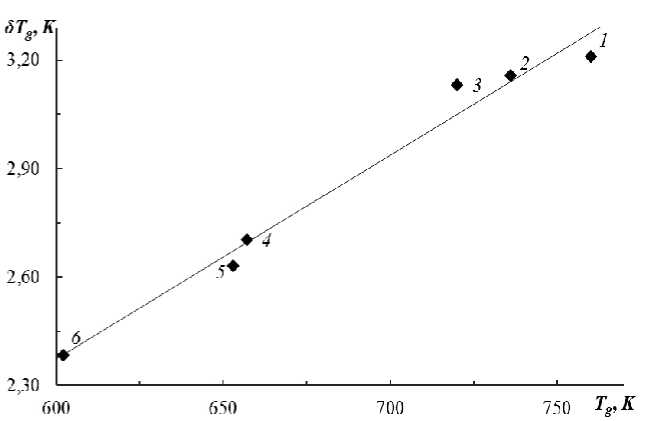
Рис. 3. Корреляция между δ T g и T g для металлических стекол. Использованы данные [8]. 1 — Fe 83 B 17 , 2 — Fe 80 P 13 C 7 , 3 — Fe 41.5 Ni 41.5 B 17 , 4 — Pd 8 ₂Si₁ 8 , 5 — Pd 77 _. 5 Cu 6 Si₁ 6 _. 5 , 6 — Pd₄ 0 Ni₄ 0 P₂ 0 .

Таким образом, параметр уравнения стеклования δT g линейно зависит от температуры стеклования T g . Этот результат имеет важное значение при выяснении природы уравнения стеклования qτ g = δT g . Ранее величина δT g рассматривалась как константа — коэффициент пропорциональности между q и 1/ τ g : чем больше скорость охлаждения q , тем меньше время структурной релаксации τ g . Полученный результат указывает на тот факт, что δT g является постоянной величиной только для стекол одного класса, у которых температуры стеклования одинаковы.

Работа выполнена при финансовой поддержке Министерства образования РФ (грант № 1932).